基于流固耦合分析方法的固定管板换热器流体对管束固有频率的影响

任子奇 梁 琳 董金善 朱 雨 张森源 冯 俊

（1.南京工业大学机械与动力工程学院；2.中国特种设备检测研究院）

流体诱导振动问题［1］是引发换热器失效破坏的主要因素之一，而这些失效破坏往往发生在换热管上。 因此，换热管的振动特性和引发换热管振动失效的机理已成为学者们的研究重点。 目前，对于有具体结构的管束振动特性的研究已经较为成熟， 可以通过多种方式去计算其固有频率，例如GB/T 151—2014《热交换器》附录C中的经验公式、TEMA标准计算方法、Macduff-Feglar计算方法、Timoshenko计算方法及Ganapathy计算方法等，通过这些计算公式可以归纳出，影响换热管固有频率的因素主要有换热管直径、 厚度、弹性模量、材料密度及几何形状等，然而在工程实际中还有各种可变因素制约着换热管的固有频率，例如折流板的尺寸、约束条件、应力、温度、换热管内外流体的介质属性及换热管内外流体对管束的影响等。 刘超锋等通过对带有折流板的换热器进行系统分析，得到了影响振动的各种因素［2］。 王健分析了换热器管束的约束条件对振动固有频率的影响，发现增加管板厚度可以提高换热管的固有频率［3］。 谭蔚等通过对换热管模型进行数值模拟，发现换热管支撑失效可能会降低换热管的固有频率［4］。 吕冬祥等通过对单根换热管进行模态分析与谐响应分析， 讨论了换热管厚度、跨距、外径和节径比对换热管固有频率的影响［5］。 任佩林等编制了换热管固有频率的计算程序，并验证了该程序的可靠性［6］。苏文献和陈功通过使用不同的换热管固有频率计算方法，对比了有限元分析结果，得出了各计算方法的区别［7］。马腾飞等使用有限元分析和试验测试两种方法对U型双金属整体螺旋翅片的振动频率和模态进行了分析， 发现U型双金属复合翅片管的频率随着圆弧弯管段半径R的增大而减小［8］。 范森等利用有限元分析软件对换热管的振动特性进行了瞬态分析、对轴向力作用下的换热管固有频率进行了分析，发现随着轴向拉力的增大，换热管固有频率增大，拉应力的加强效应小于等效压应力的应力软化效应，轴向力对换热管一阶固有频率的影响最大［9］。

在现有的标准中，影响固定管板换热器换热管振动的因素主要是壳程流体。 壳程流体横掠过换热管是引起管束振动的直接原因，壳程流体的流动对研究管束振动特性尤为重要， 而管程流体在流动过程中也会对换热管的固有频率造成影响。 为此，笔者通过Workbench软件平台， 采用流固耦合分析方法对固定管板换热器管/壳程复杂的流场流动进行分析， 以得到管/壳程流体对管束振动特性的影响规律。

1 管束振动的机理与判据

管壳式换热器在运行过程中，壳程流体的流动主要有纵向流动和横向冲刷两种状态。 由于操作工况具有多变性、 流体流动状态具有复杂性，流体在稳定状态流动时对管件产生的振动、流速瞬时变化引起的振动以及内部构件在工作过程中引起的共振等这些动力机械振动，都会引起换热管不同程度的受激振动。 其中，诱发管束振动的主要原因是横向流诱振。 虽然，纵向流所激发的振动幅值较小，危害性较低，一般情况下可不考虑它对换热管的损害，但当流体流经管道的流速瞬时变化较大时，纵向流激振会有较大幅值的变化，此时需考虑它对管束振动产生的影响［10］。

目前， 普遍认可的管束振动机理是卡门旋涡、紊流抖动、流体弹性不稳定和声共振［11］。 当壳程流体出现以下任一情况时，都有可能发生管束振动，引起管束破坏，具体情况为：

其中，do为换热管外径。

卡门旋涡频率的计算式如下：

式中 St——斯特罗哈数。

紊流抖振主频率的计算式如下：

从式（1）～（4）可以看出，换热管的固有频率是影响管束振动的一个重要影响因素。 因此，流体对管束固有频率影响的研究就显得格外重要。

2 流固耦合基本理论

流固耦合主要是研究流体与固体的相互作用，并将流体作用下的固体和静应力作用下的固体对流体的作用表现出来的一种分析方法。 在流固耦合理论使用过程中主要用到了连续性方程、动量方程和结构动力方程：

式中 ［C］——结构的阻尼矩阵，［C］∈Rnn；

{F}——结构的载荷向量，{F}∈Rn；

［K］——结构的刚度矩阵，［K］∈Rnn；

［M］——结构的质量矩阵，［M］∈Rnn；

p——流体的压强，MPa；

t——时间；

{u}——结构的位移向量，{u}∈Rn；

{u·}——结构的速度向量，{u·}∈Rn；

{u¨}——结构的加速度向量，{u¨}∈Rn；

v——流体运动速度，m/s；

ρ——流体密度，kg/m3；

τ——剪应力张量。

如果对流体做出如下假设： 流体是无粘性的，可压缩的，无流动的，流场中整体的平均密度和压强是均匀的；则上述流体的连续性方程和动量方程就可以简化为声波方程：

式中 c——声波在流体介质中的传播速度，m/s；

k——流体的体积压缩模量，N/m2；

P——声压，N/m2；

ρ0——流体的平均密度，kg/m3。

根据对流体的简化，在流体和固体的交界面上，流体法向压力梯度和固体法向加速度的关系如下：

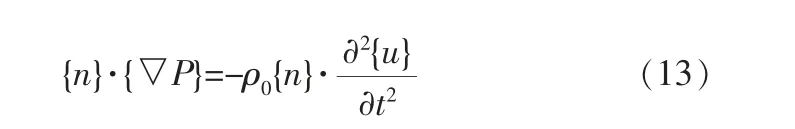
式中 {n}——耦合面的单位法向量；

{▽P}——压力梯度差。

如果考虑耦合面的影响，则声波方程可离散为：

式中 ［CP］——流体阻尼阵；

［KP］——流体刚度阵；［MP］——流体质量阵；

{p}——流体方向矢量；{p·}——流体速度矢量；

{p¨}——流体加速度矢量；ρ0［R］T——耦合质量阵。

3 固定管板换热器模型与求解

流固耦合分析方法主要有单向流固耦合和双向流固耦合两种。 其中，双向流固耦合是耦合截面上的双向数据传输，固体对流体的影响效果较为明显，不可忽略；单向流固耦合是指耦合截面上数据的单向传输，固体对流体的影响作用相对于流体对固体的影响作用效果甚微，分析过程主要是流场分析和结构场分析，而结构场的分析基于流场分析结果。

在此，笔者采用单向流固耦合方法来对固定管板换热器进行分析，考虑到固体与流体之间的相互作用力，通过Workbench平台，先进行Fluent流场分析，再将流场分析的计算结果通过耦合面传递给换热管，从而进行结构应力场分析，分析完后进行模态分析。 计算流程如图1所示。

图1 流固耦合分析流程

笔者所用模型为固定管板换热器 （图2），筒体尺寸规格为φ219mm×4mm，换热管尺寸规格为φ50mm×2mm，换热管长1 500mm，个数为7且排列角为60°，壳程流体流动方式为上进下出，管程流体流动方式为右进左出， 进出口尺寸规格为φ80mm×4mm，壳程流体介质为水。

图2 固定管板换热器模型

4 固定管板换热器流体对管束振动特性的影响

4.1 壳程流体

为了研究壳程流体对管束振动的影响，选取两种流速下换热管的固有频率进行对比，流场分析后，得到等效应力云图如图3所示。

图3 不同壳程流速下的换热管等效应力云图

由图3可知，当流速从0.3m/s上升到0.6m/s时，换热管的最大等效应力从2.014 3MPa 上升到6.522 1MPa。进行模态分析，得到换热管前六阶固有频率见表1。 分析表1中数据可知，在同一流速下，换热管的前六阶固有频率随着阶数的增大而增大；在同一阶数下，固有频率随着壳程流速的增大而减小，可见固定管板换热器壳程流速的增大对换热管固有频率具有削弱作用。

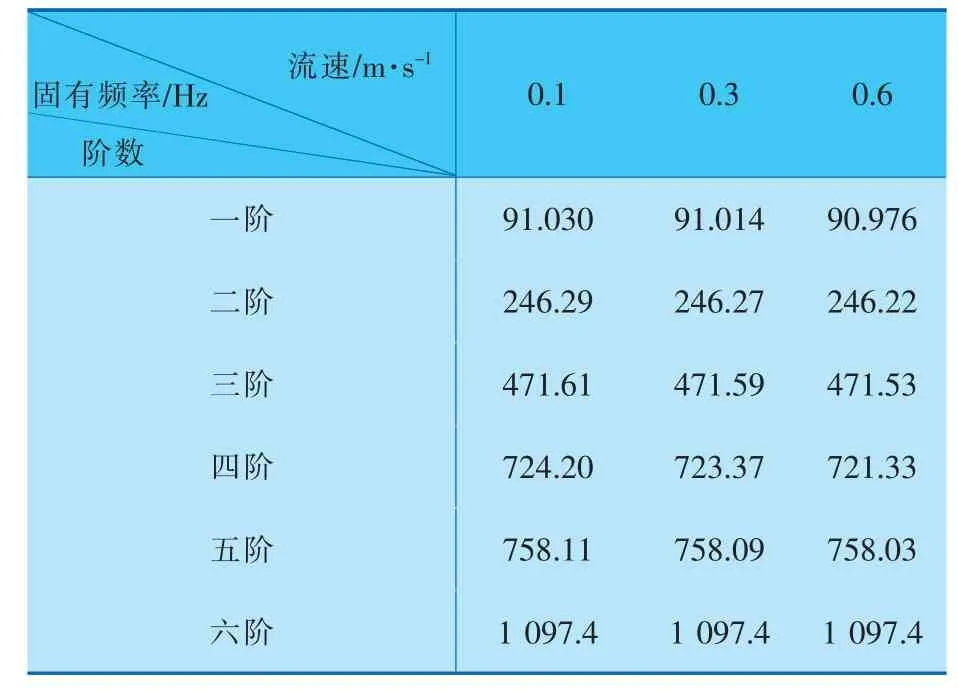
表1 不同壳程流速下换热管的前六阶固有频率

4.2 管程流体

设置流场分析的边界条件为：管程速度入口（Velocity inlet），流速分别设置为0.1、0.3、0.6m/s；其他条件与壳程流场设置一致。 流场分析结果是： 压力梯度从换热管入口处往出口处递减，出口速度低于入口速度，换热管中心速度最高并向四周递减。 通过耦合面添加流场分析结果，在静态应力场中得到等效应力云图如图4所示。 由图4可知，当流速分别为0.1、0.3、0.6m/s时，换热管的最 大 等 效 应 力 分 别 为65.712、438.860、1 077.300Pa；随着管程流速的增大，换热管所受到的等效应力越来越大，且出现位置均在流体入口处。

图4 不同管程流速下的换热管等效应力云图

对流固耦合分析后的换热管进行模态分析，得出不同管程流速下的换热管固有频率值 （表2）。 分析表2中的数据可知，在同一流速下，换热管的前六阶固有频率随着阶数的增大而增大；在同一阶数下，固有频率随着管程流速的增大而减小，可见固定管板换热器管程流速的增大对换热管固有频率具有削弱作用。

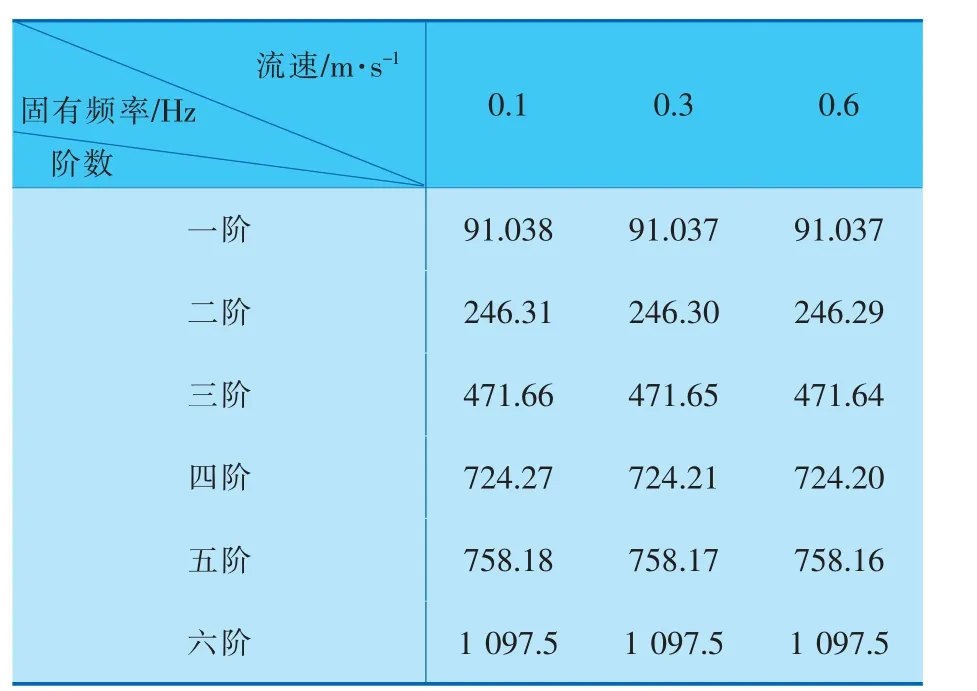
表2 不同管程流速下换热管的前六阶固有频率

5 结论

5.1 通过对比不同壳程流速下换热管的固有频率值，可以发现壳程流速对换热管固有频率起着削弱作用，依据GB/T 151—2014《热交换器》附录C中换热管固有频率的经验公式可知， 在壳程流体作用下，换热管单位长度的质量是空管质量加上被换热管排开的、虚拟的管外流体质量，因此在壳程流体的作用下换热管的固有频率会降低，并且随着壳程流速的增加，固有频率降低。

5.2 通过对比不同管程流速下换热管的固有频率值，可以发现管程流速对换热管固有频率起着削弱作用，依据相关标准，在管程流体作用下，换热管单位长度的质量为空管质量加上管内流体的质量，根据半经验公式，换热管单位长度的质量越高，换热管的固有频率越低，随着固定管板换热器管程流速的增加，固有频率降低。