基于动态矩阵控制的工业炉主蒸汽压力优化算法设计

毛丽霞

(西安铁路职业技术学院，陕西 西安 710000)

主蒸汽压力控制是工业炉自动化控制的一项主要工作，由于主蒸汽压力与工业锅炉内部温度相关，因此可以通过调节给煤量的方式来间接控制主蒸汽压力。然而在环境因素的影响下，主蒸汽压力与炉内温度之间并不存在简单的线性关系，因此需要通过计算机和特定算法的方式对工业锅炉的主蒸汽压力进行更加精确的优化，对工业炉的给煤量进行更加精确的计算[1-3]。因此，本次研究通过动态矩阵控制技术来实现针对工业炉的主蒸汽压力实施优化控制。

1 动态矩阵控制的工业炉主蒸汽压力的基本原理

动态矩阵控制的工业炉主蒸汽压力的基本原理为：依照技术单位所设置的采样时间，于各采样时刻采集工业炉主蒸汽压力实际输出值，获得该时刻下预测输出值与实际输出值之间的误差，在此基础上计算出下一时刻的最优控制量[4-5]。对所有采样时刻实施相同的操作，即将新的测量数据作为此刻的初始条件来对被控系统的未来输出加以预测，刷新优化问题并重复求解，具体步骤如下：①建立预测模型，预测主蒸汽压力控制系统的未来动态；②滚动优化，对主蒸汽压力的开环优化问题进行求解[6-7]。

动态矩阵控制算法本质上是一种反馈控制策略，即将工业炉主蒸汽压力的优化转换为“开环问题”，用下一时刻的测量值求解下一时刻的控制值[8-9]。动态矩阵控制算法的操作流程具体如图1所示。

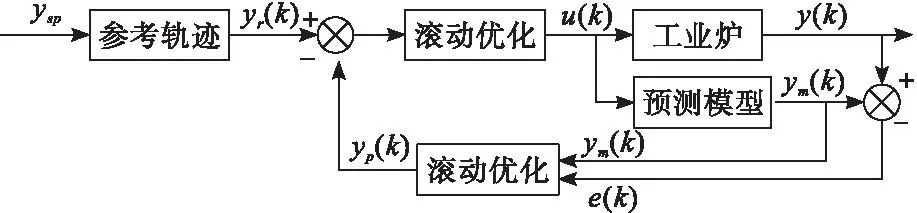
图1 动态矩阵控制算法操作流程

在图1中，ysp为设定值；yr(k)为k时刻的参考轨迹；u(k)为当前时刻的控制量；y(k)为当前时刻的实际输出；ym(k)为模型预测输出；e(k)为预测输出与实际输出值的误差；yp(k)为新的初始预测值。

2 主蒸汽压力的模型预测

动态矩阵控制需要测定锅炉燃烧系统主蒸汽压力的阶跃响应输出[10]，本次研究将给煤量u作为动态矩阵控制算法的控制量，对每一个采样时刻下的主蒸汽压力输出值进行检测，将检测结果记为a1,a2,…,aN。设N为模型截断时间，T为采样周期，由于工业炉燃烧系统是一个渐进稳定系统，在t=NT后的情况下，工业炉的阶跃响应会逐渐进入平衡状态，因此需要在该时刻下确定主蒸汽压力输出阶跃响应的稳态值[11]。本次研究通过有限集体a1,a2,…,aN来对主蒸汽压力控制回路的测量数据进行近似性的描述，即向量aN=[a1,a2,…,aN]，进而获取动态矩阵算法的首个离线参数[12]。

设k时刻下工业炉的给煤量为Δu(k)，则可通过如下公式来表示未来N个时刻的主蒸汽压力预测值：

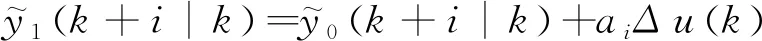
(1)

式(1)的矢量形式为

(2)

(3)

(4)

(5)

式(2)表示给煤量Δu(k)不变状态下工业炉的主蒸汽压力值。如果在未来M个采样时间点下给煤量Δu(k)发生变化，那么给煤增量则可以表示为Δu(k),Δu(k+1),…,Δu(k+M-1)，因此工业炉在未来M个时刻下的主蒸汽压力预测值可用下式加以表示：

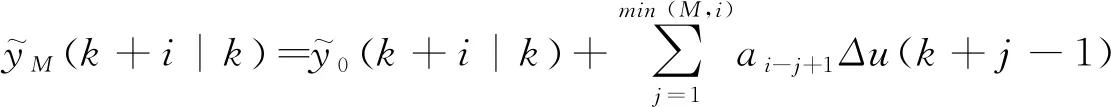
(6)

式(6)的矢量形式为

(7)

其中

ΔuM(k)=[Δu(k),Δu(k+1),…,Δu(k+M-1)]

A为动态矩阵：

3 控制量的滚动优化

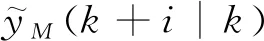
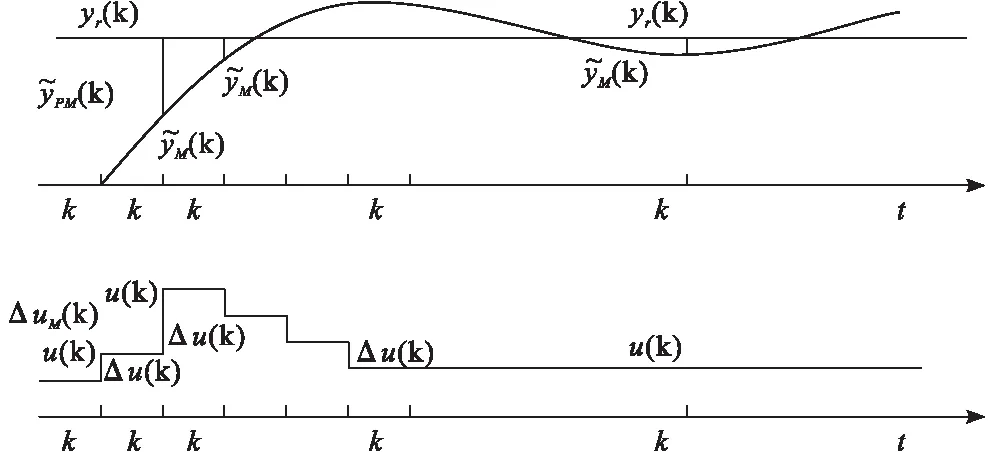
图2 动态矩阵控制在k时刻的优化策略

本次研究还借助特定的指标来对主蒸汽压力的控制效果进行判断，一方面要求系统输出与给定的期望值相吻合，另一方面确保在给煤过程中控制增量Δu(k)保持稳定。因此通过如下二次型指标函数来对k时刻的性能指标加以控制。

(8)

该性能指标的向量形式为

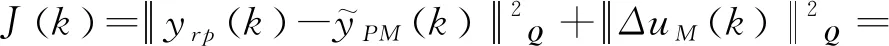
(9)

式中：Q=diag[q1,q2,…,qp]，是由误差权系数q构成的对角阵，也可称之为误差矩阵。R是由控制权系数r构成的对角阵，也可称之为控制权矩阵。

基于极值必要条件dJ(k)/dΔuM(k)=0来计算能够使优化性能指标J(k)取极小值的控制增量ΔuM(k)，处理方法如下：

ΔuM(k)=(ATQA+R)-1ATQ[yrp(k)-yP0(k)]

(10)

在此基础上，计算出k时刻优化控制所得到的Δu(k),Δu(k+1),…,Δu(k+M-1)的最优控制增量值，并在锅炉燃烧系统中引入由该时刻控制增量Δu(k)所构成的实际控制量。其中，Δu(k)为ΔuM(k)的首元素，具体表示方式如下：

(11)

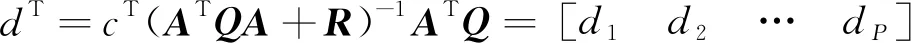
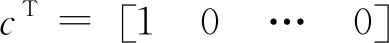
在计算出控制增量Δu(k)的情况下，则可以得出实际煤粉的控制量为

u(k)=u(k-1)+Δu(k)

(12)

4 结 语

本次研究提出了一套基于动态矩阵控制的工业炉主蒸汽压力优化算法，并给出了算法的算法模型与滚动优化方案。在未来的研究工作中，还需要进一步加强在系统的反馈校正方面的研究，进一步提升工业炉燃烧系统对于控制环境干扰的应对能力。