基于误差模型的权重二值神经网络近似加速

朱新忠，程利甫，，吴有余，林闽佳，胡汝豪

（1.上海航天电子技术研究所，上海 201109；2.清华大学 集成电路学院，北京 100047）

0 引言

当前，在航天系统中需要进行很多的图像或语音识别工作，在处理较为简单的语音任务，尤其是指令任务时，对系统实时性、高能效的要求越来越高。而深度学习已被多媒体广泛用于处理应用程序，包括图像、视频和语音的识别和分类等，其所在硬件平台也在不断发展和演进。对于航天系统而言，神经网络也逐渐被采用到简单的分类任务之中，如关键词语音命令的识别（Keyword Spotting and Recognition，KWSR）。对于网络结构逐渐复杂的深度神经网络来说，其加速所需要的硬件能耗随着网络规模的增加而迅速增加，因此，近年来近似计算和更简单的权重二值化神经网络（Binarized Weight Neural Network，BWNN）结构逐渐被引入到实时性要求高的识别加速过程中。KWSR 往往应用在物联网、手机或其他基于电池的边缘智能设备中，由于功耗和面积非常敏感，因此，简化的多层深度神经网络广泛地被应用于处理输入数据，而这些技术成熟度较高，逐渐也被航天系统所采用。

在最近几年的发展中，多类深度神经网络被应用于KWSR 或者相关的航天系统中，包括深度神经网络（Deep Neural Network，DNN）［1-2］、卷积神经网络（Convolutional Neural Network，CNN）［3-4］、基 于长期和短期记忆的递归神经网络（Long-Short Term Memory-Recurrent Neural Network，LSTMRNN）［5-6］、基于门控循环单元（Gate Recurrent Unit Network，GRUN）的神经网络［7］和卷积递归神经网络（Convolutional Recurrent Neural Network，CRNN）［8］。基于深度神经网络的KWSR 提高了语音的鲁棒性，但是其所包含的大量参数和引入的运算会产生大量在存储和计算方面的硬件开销。对于多层神经网络的压缩而言，量化是最为常用的方法之一。因此，通过探索和分析不同神经网络结构和压缩方法，BWNN 被发现可以用于实现超低功耗的KWSR［9-13］。其与传统神经网络的区别在于，传统的神经网络权重均为16 bit 或者更高的位宽，而这一网络仅需要1 bit 位宽的权重即可实现高精度的识别，即：BWNN 将权重和隐藏层二值化，激活值设为+1 或-1。这样的结构大大降低了存储压力和片上带宽压力，也因为1 bit 的位宽，几乎将网络中的乘法运算消除，仅需要优化加法运算的硬件实现。

本文提出了一个面向BWNN 的基于逐位量化的KWSR 网络，针对KWSR 中的近似加法器进行了优化设计。针对近似计算引入的误差，需要一个系统性的评估方法，本文提出了一种统计意义的误差分析模型，可用于预测近似系统对神经网络的加速效果。具体来说，使用本文的BWNN 量化方法，对不同种类的神经网络进行二值化并测试其精度，从中选取最适合的网络结构进行量化。随后，通过提出的误差统计模型，本文使用建模为软件仿真的近似加法器进行神经网络加速的精度评估。通过与功能仿真结果进行比较，本文的误差统计模型预测精度很高，最终的系统误差预测和真实系统误差对比，相对偏差约在3%以内。

1 原理分析

对BWNN 而言，一方面其权重占用的存储空间可以大大减少；另一方面可以使用位运算代替常规神经网络中的乘法操作，这样可以减少大多数乘法运算。总之，通过建立BWNN，只需要加法器就可执行几乎所有的操作，因此，我们后续对硬件的分析也集中在加法器模型上。

1.1 BWNN 系统的训练方案设计

传统对神经网络进行二值化的方法是在获得定点神经网络后进行截断并微调，这样的方式会不可避免地降低识别精度。基于权重位宽均为1 bit的XNOR-Net 的量化原理，本文提出了一种逐位量化的权重二值化方法。这一方法在网络的训练过程中介入，而非对最终的训练结果二值化，从而减少KWSR 的准确率。

量化的具体方法如下：

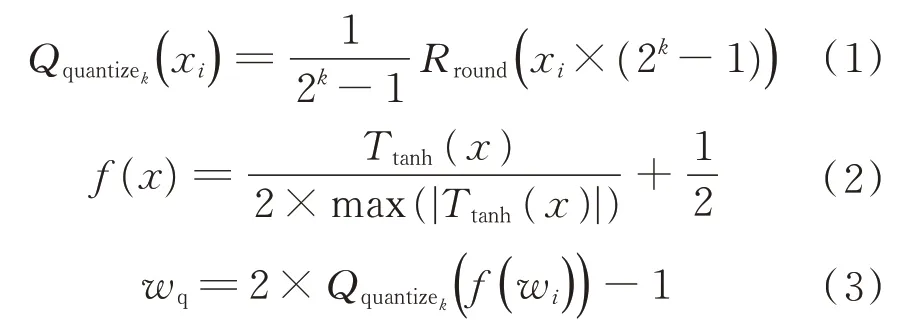
式中：wi为第i层神经网络的权重数值；k为目标的量化位宽数值；Qquantizek(·)、f(·)为量化函数和压缩函数；wq为对应的权重量化数值结果。

因此，对于任意一层的神经网络层，均有对应的量化结果。

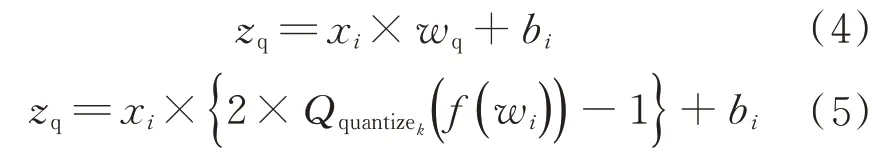
式中：xi为当前神经网络层的输入；bi为量化前的偏置量；zq为当前神经网络层的输出数值。

本文所述的逐位量化算法流程如图1 所示。

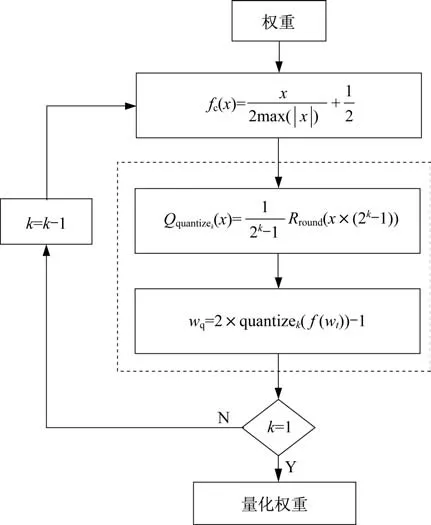
图1 神经网络的逐位量化算法流程图Fig.1 Flow chart of the bit-by-bit quantization method for neural networks

在第k比特位宽度（k＞1），输入层和批处理归一化（Batch Normalization，BN）层将同时量化。实际上，由于BN 层包含数据压缩处理，激活函数tanh的量化可以被舍弃，因此，压缩函数fc(·)可以按以下方式优化：

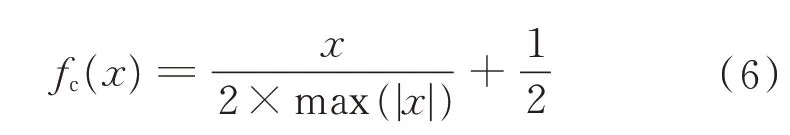
在整个量化过程中，权重是首先压缩为0～1 之间的数据。压缩数据由式（1）和式（3）得出。随后，权重量化为无损定点［-1，1］之间的数字。为了使量化权重在训练过程中更接近理想值，在处理过程中采用逐位量化的方法进行反复训练。第一次训练量化的比特位宽度和训练后的权重会保存下来以用于重新训练，并且量化的位宽在下次训练中逐渐降低。例如，量化位宽可以是从8 bit 宽度逐渐量化到4 bit 宽度，然后2 bit 宽度最终量化为1 bit 宽度。这样渐进式权重训练的最有利之处在于速度快，且可以提高权重的训练效率和可靠性。

1.2 近似加法器的概率误差分析

1.2.1 误差评估量纲

为了使描述清晰，我们首先定义准确值为Laccu，近似值作为Lappro。

最大误差量纲（Maximum Error Magnitude，MEM）即最大误差，为准确值与近似值差值的绝对值，公式如下：

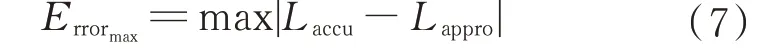
相对误差量纲（Relative Error Magnitude，REM）即相对误差，为准确值、近似值差值的绝对值和准确值绝对值的比，公式如下：

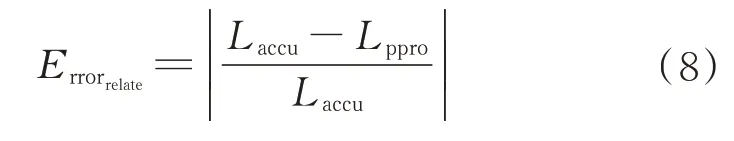
平均误差量纲（Average Error Magnitude，AEM）为绝对差大小介于精确值和近似值之间所有差值的平均数，平均误差满足如下公式：

均方误差量纲（Mean Squared Error Magnitude，MSEM）为在所有可能的精确值与近似值之间的大小距离值上取平均，平方误差度量公式如下：

1.2.2 低延迟近似加法器模型

基于文献［9］中的研究内容，代表基于块的通用模型加法器结构如图2 所示。输入位分为多个不相交或重叠的子加法器。每个子加法器产生相应输入的输出部分和，同时使用前面子加法器的输出进位来生成结果。

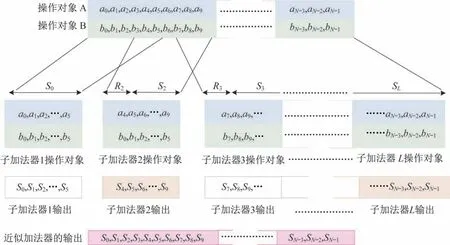
图2 基于块的通用模型加法器结构［6］Fig.2 Structure of generic block-based approximate adder［6］

文献［6］中提出的误差模型如下：

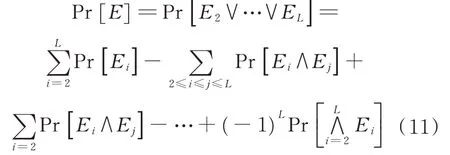
式中：Ei为二进制变量，当第i个子加法器错误时，Ei=1，否则Ei=0。考虑任何第i个加法器，当2≤i≤L，Ei=1，会有

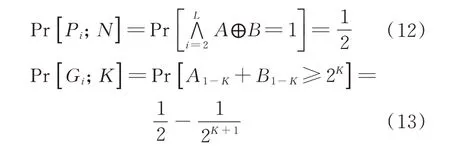
式中：A1-K+B1-K为没有输入到第i个子加法器的较低比特位置；Pr[Pi；N]为之前的子加法器生成的进位数值参与计算；Pr[Gi；K]为之前的较低有效位在第i个子加法器产生一个进位；N为加法器的位宽；K为产生进位的低比特数据位宽；⊕为异或运算符；Pi为第i个子加法器产生了进位这一事件；Gi为第i个子加法器的低比特位产生进位这一事件。

1.3 近似加法器阵列的误差统计模型

对于由近似加法器组成的近似计算阵列，可分为两种不同的情况：如果加法器用于不同的计算源，例如不同的神经元，其误差统计模型则为单独考虑，近似加法器阵列的误差模型是所有加法器的最大误差，即MEM 值；如果近似加法器形成一个累加结构，将阵列的误差模型视为所有加法器的平均误差，即AEM 值。

2 实现方案

在这一部分，进行了以下实验。首先，本文为KWSR 系统设计了各种网络，见表1，它们由不同的层组成；然后，将所有网络通过前述的方法进行二值化，对于模型验证，使用Matlab 模拟近似加法器的功能行为并获得BWNN 的准确性；最后，将误差模型引入BWNN 以获得模型输出精度，两者精度在本文末尾进行了比较。

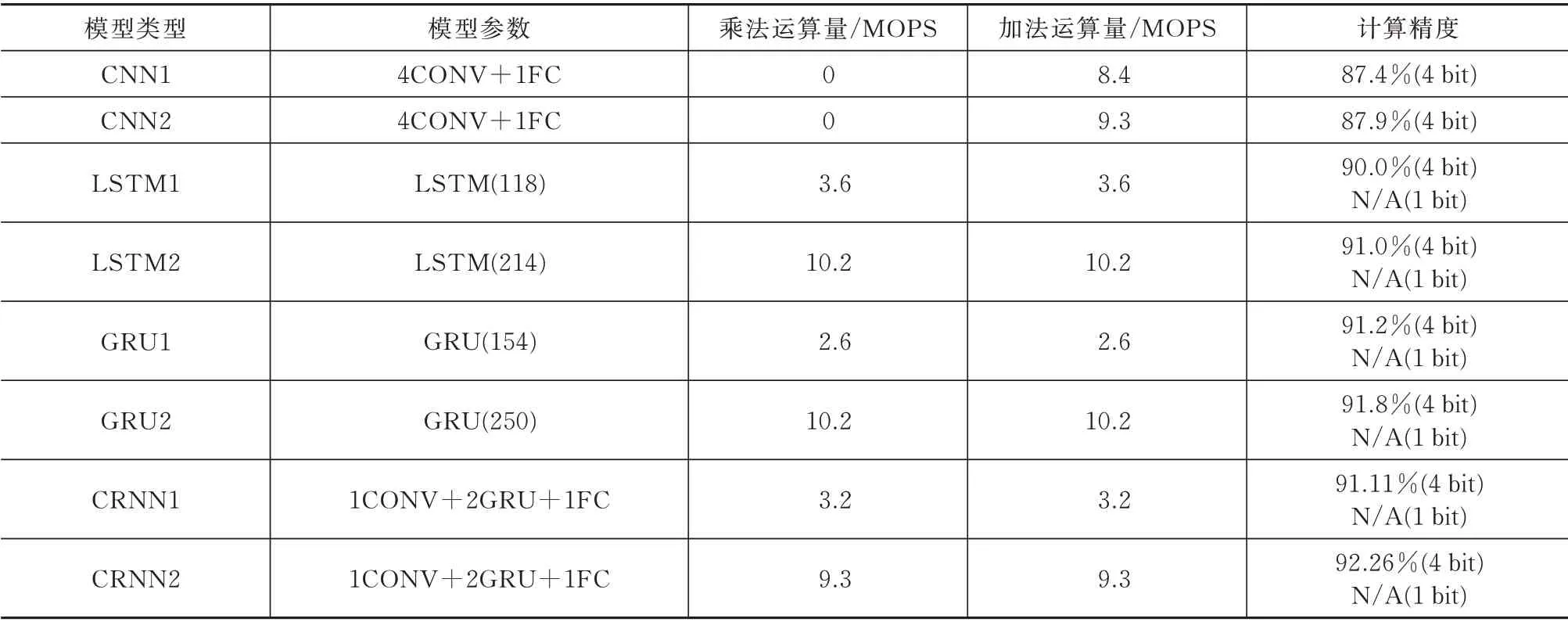
表1 深度神经网络的实现方案与对比Tab.1 Implementation schemes and specifications of DNN models

2.1 BWNN 的设计

使用Google 语音命令数据集（Google Speech Command Dataset，GSCD）作为训练集和验证集。GSCD 中有10.5 万组1 s 长的音频数据，集中包含35 个关键字的片段。当训练神经网络时，我们将卷积层的权重和完全连接的层量化至1 bit 位宽。BWNN 模型经过培训，可以将音频识别分类为10个关键字之一，“YES”“NO”“UP”“DOWN”“RIGHT”“LEFT”“ON”“OFF”“STOP”“GO”“沉默”（即不说任何话）和“未知”（即所说词语不在10 个关键词以内）。

表1 总结了所测试的神经网络的层次类型、计算要求和准确性，其中部分结构来源于文献［5-6，14-16］中采用GSCD 进行KWSR 命令的网络。这些网络架构的权重都进行了二值化测试。其中缩写的含义：CONV 为卷积层，FC 为全连接层，LSTM 为LSTM 单元的个 数，GRU 为门递归单元个数。

表中可见，LSTM、GRU 和CRNN 都比CNN 的精度更高，但是它们在二值化后无法得到收敛的结果，即无法进行二值化。而为了提高语音识别的鲁棒性并降低电路的功耗，可以适当牺牲网络的识别精度，同时还需要控制识别精度高于85%。因此，CNN 是适用于BWNN 的结构。

2.2 二值化权重神经网络的实现

由于权重在整个KWSR 系统中加载后，计算过程将不会更改，而数据将在整个操作过程中不断变化，需要减少权重占用的存储和数据刷新速度以进一步降低功耗。因此，需要根据网络规模来评估和优化网络卷积核、全连接层的权重第1 和第2 卷积层的输出。本文将3×3 卷积核用于卷积运算，同时减少数据位宽并防止数据溢出。而最后卷积层的输出结果直接影响第一全连接层的权重大小。因此，本文减少了卷积层的卷积核数量，并增加卷积核的步幅以减少输出结果的大小。

3 验证结果与分析

基于上述的方法，在实现了4 个BWNN 之后，评估了错误在软件仿真结果和模型输出结果之间，见表2。对于提出的4 个BWNN，仿真系统精度和预测系统精度之间的相对差异约为2%～3%。结果表明，采用的误差统计模型可以预测本文所叙述的计算系统的精度。其中4 个网络的拓扑结构阐述如下：BWNN 1～4 均由4 层卷积、1 层全连接（30 个神经元）组成，卷积层参数（通道数、卷积核的三维尺寸、步长）见表1。通过4 种不同的卷积网络设计，可以应对不同复杂度的分类场景，针对不同步长、不同通道数均进行了验证，体现了模型的精确性和普遍适用性。

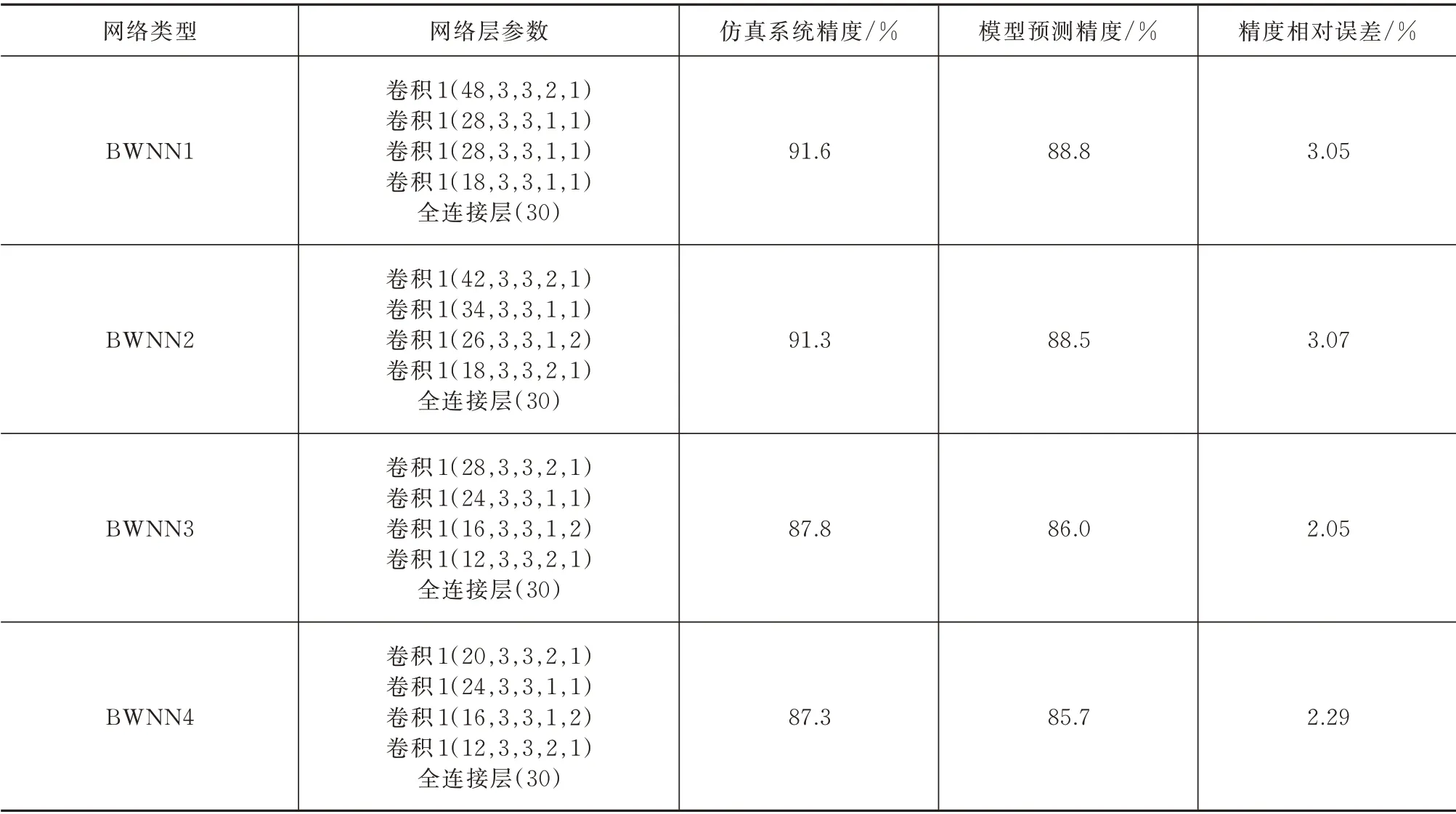
表2 系统误差的预测和实测对比Tab.2 Predicted and simulated accuracies

4 结束语

本文提出了系统的误差统计模型，可用于BWNN 在近似加法器的近似加速系统中。本文为KWSR 提出了二进制加权神经网络的量化方法，参考了近似加法器的基本误差模型并针对KWSR 系统进行了优化。此外，对面向10 个命令词识别的网络进行实验，并将其二值化为BWNN。通过使用误差统计模型，可以预测BWNN 的系统精度。通过比较仿真结果和模型预测的系统精度，本文提出的方法可以实现3%以内的精度预测相对损失。这一工作对后续航天系统中KWSR 的系统设计，提供了有力的工具。