基于帝国竞争优化的双目标综合决策选星算法

邱明 严勇杰 孙蕊 张文宇

(1. 南京航空航天大学 民航学院, 南京 211106; 2. 空中交通管理系统与技术国家重点实验室, 南京 210007)

随着全球卫星导航系统(GNSS)的快速发展,其被广泛运用在工程应用中(测量、导航等)为人类带来了巨大的社会和经济效益[1]。 然而,快速发展的同时对目前的全球卫星导航系统的导航性能提出了更高的要求,其中包括更好的实时性、更高的精度和更强的可靠性。 在此背景下,各国大力发展自己的全球卫星导航系统,其中包括中国的BDS、美国的GPS、俄罗斯的GLONASS 以及欧盟的Galileo。 全球卫星导航系统随着多星座建设的发展,未来四大全球卫星导航系统将提供超过百颗的卫星供用户接收机进行导航服务[2]。 虽然,这将极大提高用户的可用卫星数,然而过多的可见卫星提供的冗余信息也会增加接收机导航定位解算的耗时。 在满足实际应用过程中定位结果的精度要求下,为了提高接收机实时解算的性能,可以从接收机观测到的所有可见卫星中挑选出几何布局较好的星座进行定位解算[3],这种选取卫星的方法称之为选星。 目前的选星算法从单卫星导航系统选星发展而来,一般通过最小几何精度因子(Geometric Dilution Precision, GDOP)方法、遍历法或者最大体积法选取固定数目卫星中几何构型最好星座进行解算[4-5],但计算量巨大,无法保 证 实 时 性。 Mosavi 和 Divband[6]认 为 最 小GDOP 方法在实践中仍然是首选的卫星选择方法,剩下的问题是简化GDOP 的计算,为了提高计算效率,其提出了基于进化算法(EA)的自适应滤波技术来计算GDOP 的方法,结果显示,可用自适应滤波技术的算法近似计算GDOP,但还是存在着一定的误差[6]。 为了提高准确性,后续的研究人员提出了其他的改进算法。 王尔申等[7]基于粒子群优化(Particle Swarm Optimization, PSO)算法固定选星数目,依据最小GDOP 值进行选星,降低了选星耗时,提高了选星的有效性。 霍航宇和张晓林[8]将多系统选星算法视作单目标优化,根据用户所需精度固定不同的卫星数目进行定位解算。 Azami 和Sanei[9]运用神经网络算法对星座的GDOP 进行分类,更快地获取GDOP小的卫星星座。 宋丹等[10]也将遗传算法用到选星中,结果表明, 遗传算法比遍历法耗时短。Wu 等[11]基于支持向量机算法逼近星座的GDOP,避免计算时复杂的矩阵求逆转置等步骤。 刘季等[12]也从高度角出发以及考虑GDOP值进行组合选星。 但上述几种选星算法都是先固定选星数目,再在所有的固定卫星数目星座中选出最小GDOP 的卫星星座。 可是实际运用于接收机时,接收机观测卫星数会随着时间发生变换,同时随着四大全球卫星导航系统的发展,用户接收机观测到的可见卫星将多达几十颗,此时提前固定选星颗数值得商榷。 因此,当前的选星算法存在着不能灵活的固定选星数目的问题,具有很大的局限性。 有必要同时考虑卫星数目和定位结果的精度,从这2 个目标出发进行选星。

近年来有学者从多目标优化出发,如徐小钧等[13-14]基于NSGA-II 遗传算法将GDOP 值和选星数目视作2 个目标进行多目标快速选星,仿真表明其在静态和动态情况下有良好的表现。 虽然运用遗传算法进行多目标优化是一个可行的方法,然而过程比较繁琐,同时选星时未考虑引入卫星仰角和方向角等先验信息。 针对上述选星算法存在的问题,本文采取了基于帝国竞争优化算法(ICA)的双目标综合决策选星算法。 充分利用帝国竞争优化算法的复杂度低、计算量少的优点以及利用所选星座的GDOP(能够间接反映出定位结果的精度)和选星数目2 个目标进行综合决策;为了更好地获取几何构型好的卫星星座,本文通过引入可见卫星的卫星仰角和方向角先验信息,进行先验性约束,有效解决了呆板的固定选星数目的问题。 同时在双目标综合决策时,不采用复杂度高的多目标优化算法,而是依据2 个目标的相关性,将2 个目标结合成1 个联合目标进行综合决策,极大降低了算法的复杂性,从而缩短了计算时间。 因此,卫星接收机不仅不需要提前固定选星数目,还能提高接收机的计算效率,同时引入先验性约束后的选星结果的GDOP 值满足用户精度要求,较无约束下的选星后的GDOP 值有所减小,对定位有重要意义。

1 多星座GDOP

在全球卫星导航系统中,用户通过接收机获得的自身定位结果精度与接收机中观测到的可见卫星组成的卫星星座的几何构型以及测量的伪距值的误差有关,其中卫星星座的几何构型可以用GDOP 来反映[13]。

式中:下标GPS、GLO、GAL、BDS 分别代表GPS、GLONASS、Galileo 和BDS 系统[13];H为一个n×7维的观测矩阵,n为接收机观测到的全部卫星导航系统下的总可见卫星颗数;HGPS为GPS 系统下的观测矩阵的前3 列;HGLO、HGAL、HBDS分别为GLONASS、Galileo、BDS 卫 星 导 航 系 统 下 观 测 矩阵的前3 列;H的后4 列中,1x和0x分别为x卫星导航系统下对应可见卫星数目维全为1 和0的列向量[13]。 同时,为了进一步从接收机的角度讲述多星座选星的意义,本文从卫星可见数目出发,分析选星数目与GDOP 的关系,选取GPS +GLO + BDS 三系统下一个历元采集到的数据,其观测到的可见卫星总数为25,确定不同选星数目(在三系统下,有6 个未知数,因此选星数目从6 出发),采用最小GDOP 方法,将不同选星数目下选星后的最小GDOP 值与全部可见卫星下计算得到的最小GDOP 值记录,其结果如表1 所示。

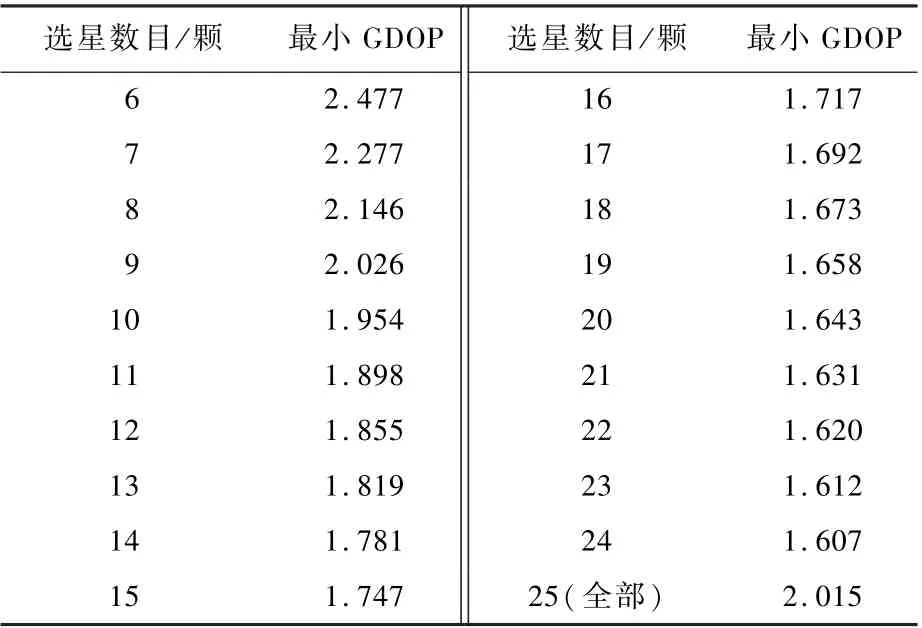
表1 GPS +GLONASS +BDS 下不同选星数目后的最小GDOPTable 1 Minimum GDOP with different numbers of selected satellites (GPS +GLONASS +BDS)

2 基于帝国竞争优化的选星算法

可知,随着选星数目的增加,GDOP 值非线性递减, 同时GDOP 下降越慢,选星数目超过9 后的GDOP 比全部可见卫星下的GDOP 还小,这说明全部可见卫星中存在某些卫星使全部可见卫星下的几何构型变差,导致GDOP 值变大。 从而选星可能不仅能够降低可见卫星数目,减少接收机的功耗,也可能在选星过程中,删除一些几何构型差的卫星。 因此,本文为了使选星后的卫星星座的几何构型尽可能较好,依据可见卫星的方向角和卫星仰角先验信息,引入先验性约束,将所有的可见卫星按照方向角0° ～90°,90° ～180°,180° ～270°,270° ～360° 4 个区间,划分到对应不同区间,再从每个区间中选取该区间下卫星高度角最大的卫星,从而使卫星分布较广,如图1所示,菱形点为引入先验性约束后选取的初始4 颗卫星。

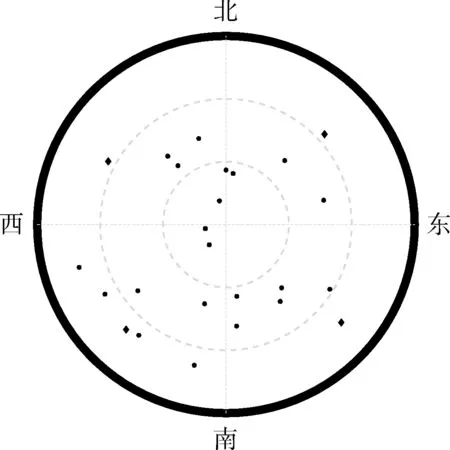
图1 先验性约束下选取的初始卫星Fig.1 Initial satellites selected with a priori constraint

针对从多个卫星导航系统的可见卫星中快速选出几何结构较好的星座,本文提出一种基于帝国竞争优化的双目标综合决策选星算法。 帝国竞争优化算法是一种通过模拟帝国主义殖民竞争机制进行随机优化搜索的算法[15]。 基于帝国竞争优化算法,本文首先根据卫星接收机接收到的卫星数据中观测到的卫星总数进行编码,引入可见卫星的卫星仰角和方向角先验信息,初始化原始国家时依据卫星仰角和方向角进行先验性约束;然后计算原始国家的GDOP 和选星数目双目标联合决策成本值来划分初始帝国,根据划分的对应帝国来同化帝国对应分配的殖民地,同化后进行国家改革,所有国家改革后,进行帝国更换,更换后的不同帝国相互竞争,强大帝国夺取弱小帝国殖民地,弱小帝国无殖民地后灭亡,沦为强大帝国殖民地;最后收敛出最优结果,进行译码,得出所选卫星号。 图2 为详细的算法流程。

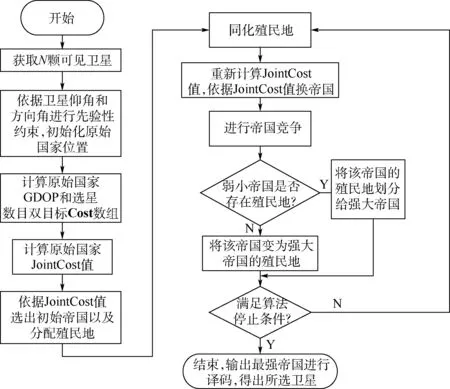
图2 基于帝国竞争优化的选星算法流程Fig.2 Process of ICA satellite selection algorithm

该算法的主要步骤如下:

步骤1 将所有符合条件的可见的卫星提取出,得到其总数N。

步骤2 初始化系统参数和帝国。 其中初始化帝国包括初始化殖民地以及原始帝国2 个部分。 首先根据可见卫星总数N,将所有卫星编号为1 ～N,将所有的可见卫星按照方向角0° ～90°,90° ～180°,180° ～270°,270° ～360° 4 个区间,划分到对应不同区间,从每个区间中选取该区间下卫星高度角最大的卫星,对应卫星编号位置编码为1,根据设定的国家数nPop,随机选取nPop 种组合为原始国家,即在其他卫星编号位置处将选取到的卫星在对应卫星号编码为1,没有选取到的卫星对应编码为0。 将该原始国家的连续N个编码作为原始国家的位置,建立一个N维变量的数组来表示原始国家的位置,即X。

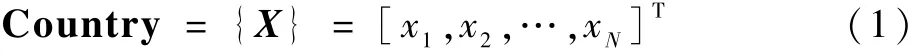
计算每个原始国家的成本(Cost)值:

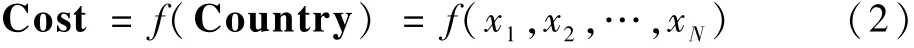
式中:f(·)为计算成本Cost 值的函数。 本文中Cost 值指的是每种组合的GDOP 值和选取的选星数目的二维数组。 得到所有原始国家的成本值后,计算一个双目标联合决策成本值JointCost,这是因为本文算法计算的成本值是二维数组,无法直接比较,但是通过表1 结果分析可知,当卫星数目增多时,其对应的GDOP 值下降,可知选星数目与GDOP 值存在相关关系。 因此,可以将二者联系起来,形成一个双目标联合决策成本值Joint-Cost。 为了计算出该联合成本值,设计了一个对应计算函数,具体公式如下:

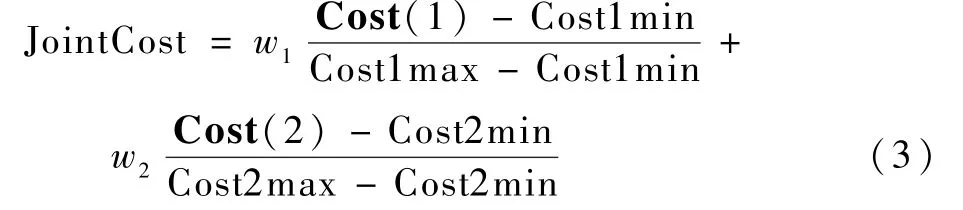
式中:w1和w2为对应的权重,取决于用户的偏好,也能更好反映出当考虑卫星数和GDOP 两个成本值时,算法可以人为地选择偏重哪一方,从而使接收机更有灵活性;Cost(1)和Cost(2)分别为原始国家成本值二维数组中的选星数目和GDOP值;Cost1max 和Cost1min 分别为所有原始国家成本中选星数目的最大值和最小值;Cost2max 和Cost2min 分别为所有原始国家成本中GDOP 最大值和最小值。 计算完所有原始国家的联合成本值后,将初始化帝国。 选取帝国的原则是依据每个国家的权力值选取权力值大的前几个国家为帝国。而国家的权力值与国家的联合成本值成反比,即联合成本值小的国家,权力则大。 因此,本文将联合成本值低的前几个国家选取为帝国,然后依据每个帝国的权力值将未成为帝国的国家视作殖民地,对其进行划分[16]。 分配殖民地时,首先标准化每个帝国的联合成本,确定每个帝国的权力值。

式中:cM为第M个帝国的联合成本值;CM为第M个帝国的标准化联合成本值; max{ci} 为全部帝国中最大联合成本值。 有了所有帝国的标准化联合成本值后,定义每个帝国的权力为

式中:MCM为第M个帝国的殖民地的数量;Mcol为殖民地总数,即未能成为帝国的原始国家总数;round 为取整函数,即将PM·Mcol的结果按照四舍五入取整。

步骤3 同化殖民地。 帝国为了巩固在殖民地中的主体地位,迫使殖民地学习自己的文化,这种控制殖民地的方式称为同化。 在帝国竞争优化算法中,将同化的方式模拟为让殖民地的位置向帝国的位置靠近。 其中每个殖民地向帝国靠近的距离为y～U(0,β×d),即y是一个在β×d内均匀分布的随机数[16],d为殖民地与帝国之间的距离,β一般取值大于1。 具体同化的公式如下:

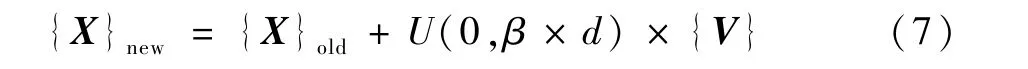
式中:{V} 为殖民地靠近帝国时的移动方向;{X}old为殖民地原先位置;{X}new为殖民地同化后的位置。 同化殖民地后,重新计算帝国和帝国下的殖民地对应的双目标联合决策成本值,如果殖民地中新计算的联合成本值小于帝国的联合成本值,则将该殖民地替换为新的帝国,也称为换帝。

步骤4 国家改革。 由于最开始的帝国竞争优化算法会陷入局部最优解,后续研究者加入了国家改革这一环节。 事先设定国家发生改革的概率,如果该国家发生了改革,则将改革后的成本值与改革前进行比较。 由于本文国家的成本值为GDOP和选星数目双目标二维数组,无法直接比较,按照双目标联合决策成本值计算公式,计算对应的值,取小者对应的位置为该国家新的位置。 这样就能使帝国和殖民地在一定概率下都能进行位置的自我更新,缓解了算法陷入局部最优解的难题。

步骤5 帝国竞争。 为了更好体现不同帝国竞争时帝国之间的权力值,帝国竞争时将考虑帝国的成本值以及所拥有的殖民地的成本值,即总成本值。 因此,首先计算帝国的总成本值。 然后根据帝国的总成本值确定其权力值,其总成本值计算公式为

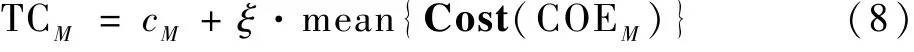
式中:TCM为第M个帝国的总成本值;0 <ξ<1;mean{Cost(COEM)}为该帝国所有殖民地的联合成本值JointCost 的平均值。 由于本文成本值为双目标二维数组,将总成本计算公式中的成本值cM替换为对应帝国及其殖民地的双目标联合决策成本值JointCost。

最后和初始化帝国时标准化帝国的联合成本值一样,标准化所有帝国的总联合决策成本值,得到每个帝国的标准化总联合决策成本值MTCM。

D中最大值对应权力最强大帝国, 然后权力最强大帝国掠夺D中最小值对应帝国的殖民地。

步骤6 帝国灭亡。 如果最弱帝国没有殖民地了,则划分为权力最大的帝国的殖民地。 判断是否迭代完毕,如果没有,则返回步骤3,迭代完毕则输出最后结果。

步骤7 输出最后结果。 即双目标联合决策成本值最小的帝国,然后将得到的结果进行译码,即该帝国位置中编码为1 的卫星号,为所需要选取的卫星。 同时提取出对应的成本值,即对应的卫星数目以及GDOP 值。 通过其GDOP 值以及选星数目,可以验证算法的有效性。

3 实验仿真与实测数据

3.1 GPS +GLONASS +BDS 仿真

为了验证本文算法的实时性以及有效性,仿真了3 个全球卫星导航系统下卫星数据,3 个全球导航系统分别为GPS、GLONASS、BDS。 在3 个全球卫星导航系统组合导航的情况下,进行了仿真,仿真时间为24 h,仿真地点为南京,地理坐标为北纬32°02′38″、东经118°46′43″。 通过本文算法的单次选星耗时来反映实时性,以及通过算法引入先验性约束和无先验性约束下最后选星结果中的GDOP 与实测数据中总可见卫星数目的GDOP 进行对比和选星数目是否降低2 个方面来反映算法的有效性,同时由于在实际接收机进行解算的时候,会筛选出高度角小的卫星,使定位结果更加准确。 因此,为了进一步验证本文算法,选取仿真中高度截止角5°和10°下的实验数据进行验证。

3.1.1 有效性分析

高度截止角5°和10°仿真条件下的选星前后对比如图3 和图4 所示,表2 为统计分析,表3 为缩减卫星时,本文算法无先验性约束和先验性约束下的平均选星数目比较。

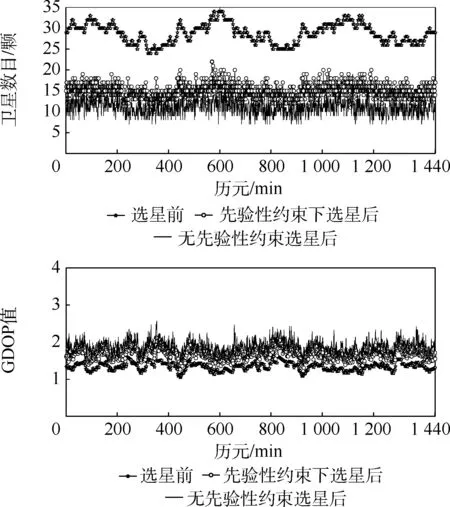
图3 截止高度角5°下的选星前后对比Fig.3 Comparisons before and after satellite selection with an elevation angle of 5°

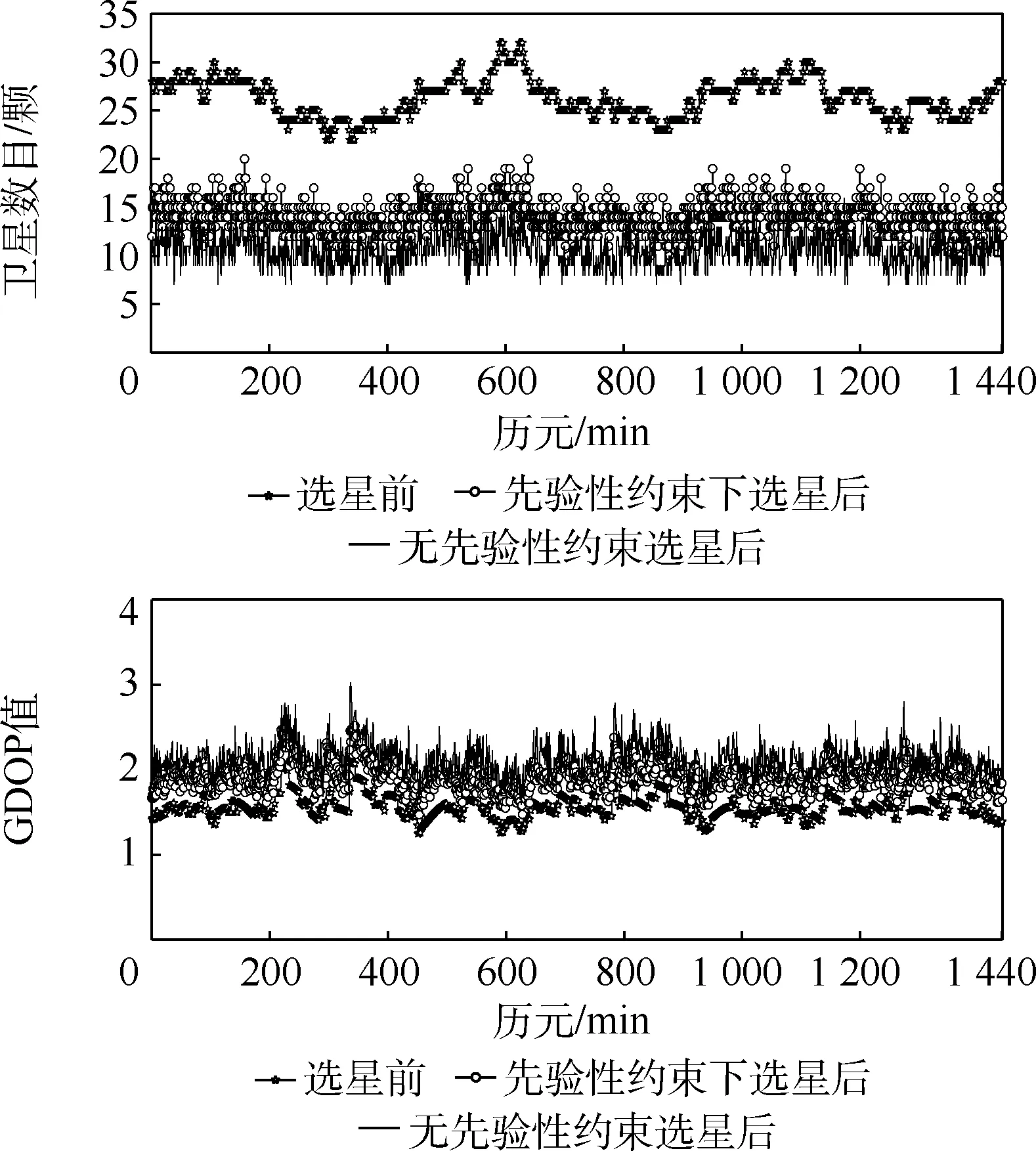
图4 截止高度角10°下的选星前后对比Fig.4 Comparisons before and after satellite selection with an elevation angle of 10°

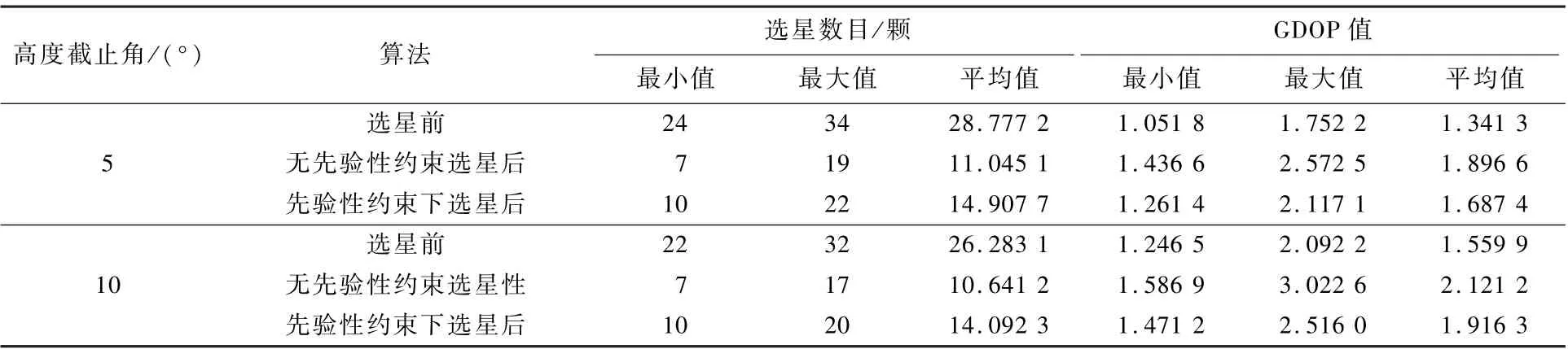
表2 GPS +GLONASS +BDS 下选星前后对比分析Table 2 Comparative analysis before and after satellite selection (GPS +GLONASS +BDS)

表3 有/无先验性约束下平均选星数目对比Table 3 Comparison of average satellite selection number with /without a priori constraint

从图3、图4 的关系曲线以及表2、表3 的统计分析中,可得出以下结论:

1) 当高度截止角选取为5°和10°时,本文算法无论有无先验性约束选星数目总体变化趋势都与仿真下的总可见卫星颗数相似,同时对应的GDOP 变化趋势同样与其总可见卫星颗数对应星座的GDOP 变化趋势相似,说明本文算法具有稳定性。

2) 高度截止角为5°时,无先验性约束下选星后的选星数目的平均值为选星前的38.4%,当高度角选取为10°,选星后的选星数目的平均值为选星前的39.9%,当引入先验性约束后,选星后的选星数目在高度截止角为5°和10°下,分别为51.8%和48.97%。 说明无论是否存在约束本文算法都能够充分降低选星数目。 同时如表3 所示,高度截止角为5°下引入先验性约束后缩减率51.8%较无先验性约束下的缩减率38. 4% 增加了13.4%,说明引入先验性约束后选星数目增加了,但是相对于选星前的总可见卫星数依旧减少了48.2%,有效降低了卫星数目。

3) 当引入先验性约束后,在高度截止角5°和10°下,选星后的GDOP 平均值1.687 4 和1.916 3相对于无先验性约束选星后的1.896 6 和2.121 2降低了0.209 2 和0.204 9,说明引入先验性约束后,本文算法更能有效地选取几何构型好的卫星星座。 同时,当GDOP 值小于6 时,满足全球卫星导航系统的有效性要求,但为了用户拥有更好的精度,通常需要将GDOP 值控制在4 以内的范围[17]。 本文算法无论是否引入先验性约束,选星后都将GDOP 控制在小于4 的范围内,说明本文算法能够满足用户精度要求。 同时,为了进一步描述引入先验性约束后选星前后的GDOP 变化,本文对整个仿真过程中引入先验性约束后的选星后的GDOP 与选星前(总可见卫星数的GDOP)的差值进行分析,其中高度截止角5°和10°下的选星前后GDOP 差值的统计分析如表4 所示。 前后GDOP 差值的方差用来表示差值的稳定程度,从而反映选星算法的稳定性。

表4 选星前和先验性约束下选星后GDOP 差值在各区间下的百分比Table 4 Percentage of GDOP difference before and after satellite selection with a priori constraint in each interval

如表4 所示,本文将每次引入先验性约束后的选星前后GDOP 差值划为[0,0.1),[0. 1,0. 2),[0.2,0.3),[0.3,0.4),[0.4,0.5]5 个区间,由表4 可知,选星前后GDOP 差值主要分布在[0.3,0.4)区间,与选星后的GDOP 平均值相对于选星前的GDOP 平均值增加量小于0.4 一致。同时选星前后GDOP 值的差值的方差较小,说明选星前后GDOP 差值比较稳定,保持了良好的有效性。

3.1.2 实时性分析

在高度截止角5°仿真条件下引入先验性约束和无约束下的单次选星耗时对比如图5 所示,表5 为统计分析,表6 为有无/先验性约束下单次选星平均耗时与遍历法对比。

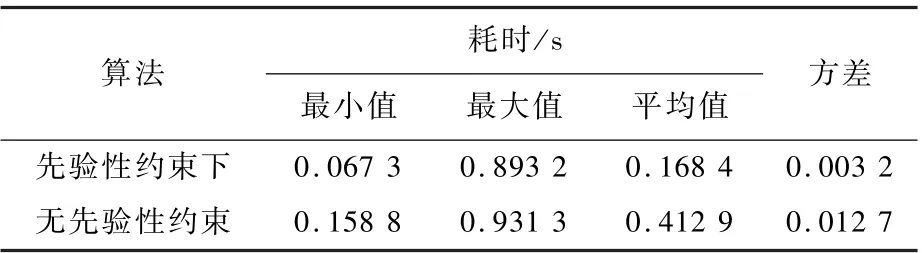
表5 截止高度角5°下有/无先验性约束单次选星耗时数据统计Table 5 Statistics of time consumption for one-time satellite selection with/without prior constraint at an elevation angle of 5°

表6 单次选星平均耗时算法性能比较Table 6 Comparison of time consumption of one-time satellite selection by candidate algorithms

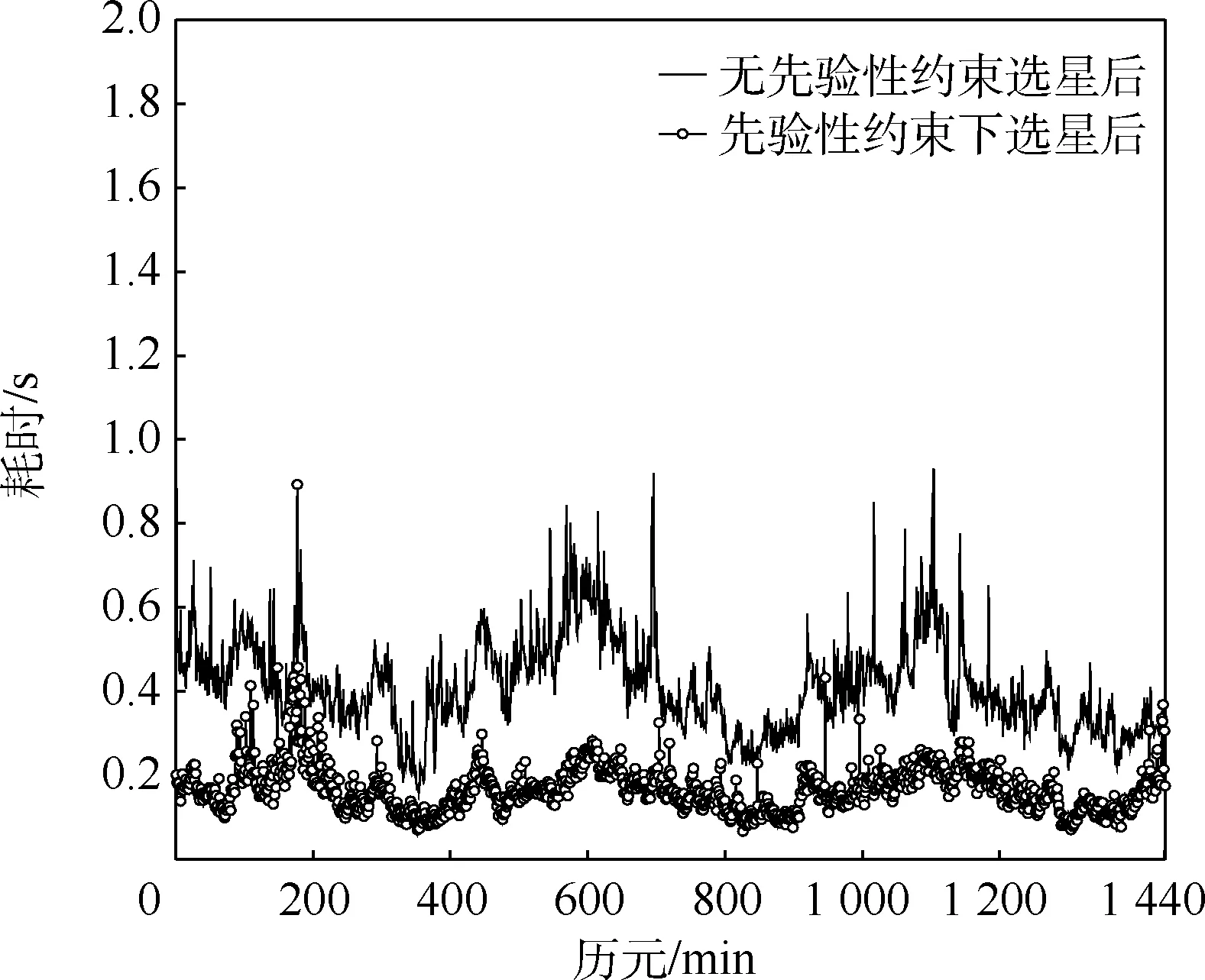
图5 截止高度角5°下有/无先验性约束单次选星耗时Fig.5 Time consumption of one-time satellite selection with/without prior constraint at an elevation angle of 5°

从图5 的关系曲线以及表5、表6 的统计分析中,可得出以下结论:

1) 在高度截止角选取为5°时,本文算法在无约束条件下单次选星所用最长时间为0.931 3 s,引入先验性约束后,单次选星所用最长时间为0.893 2 s,两者都比遍历法的4 s 所用时间少,分别提高76.72%和77.67%,实时性强。

2) 在高度截止角选取为5°下,本文算法在无约束条件下和约束下单次选星所用平均时间分别为0.412 9 s 和0.168 4 s,说明引入先验性约束后,算法耗时降低,两者相对于遍历法4 s,分别提高了89.68%和95.79%,进一步说明本文算法的实时性。

3) 无论是在无约束条件下还是引入先验性约束后,选星所用时间的方差都较小,说明本文算法选星耗时方面稳定性强,具有良好的实时性的同时依旧保持着有效性。

3.2 GPS +GLONASS +BDS 实测数据

为了验证本文算法在实际运用中的有效性以及实时性,本文在南京航空航天大学收集了GPS +GLONASS + BDS 系统的实测数据,对选星情况进行了实测数据验证,时长为2 h,实验地点为地理坐标(北纬31°56′20″、东经118°47′04″),高度截止角选取为5°,采集数据环境如图6所示。

图6 采集数据环境Fig.6 Environment of data collection

3.2.1 有效性分析

实测数据高度截止角5°下的选星前后对比如图7 所示,表7 为统计分析。

从图7 的关系曲线以及表7 的统计分析中,可得出以下结论:

表7 实测数据下选星前后对比分析Table 7 Comparative analysis before and after satellite selection based on field data

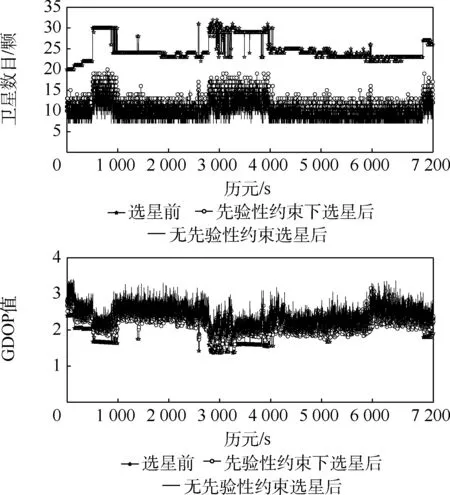
图7 实测数据下选星前后对比Fig.7 Comparison of satellite selection before and after based on field data

1) 在实测数据下以及高度截止角选取为5°时,本文算法在先验性约束下所选的平均卫星数目较平均总卫星颗数明显降低,缩减率达45.4%,较无约束下的35.7%有所增加,但依旧可以大大降低卫星数目。 同时由于采集的数据为2 h,卫星总数总体变化趋势较为平稳,但是本文算法选星后的卫星数没有固定,会发生变化,说明可以灵活地进行选星,比一般提前固定选星数目具有更强的机动性。

2) 在实测数据下以及高度截止角选取为5°时,在先验性约束下选星后的GDOP 平均值2.237 3相对于选星前的GDOP 平均值2.060 0 增加量小于0. 2,相对于无约束下平均GDOP 值2.485 7减少了0.248 4,说明在实际采集的数据中,引入先验性约束后,本文算法能够从全部可见卫星中选取更多几何构型较好的卫星,因此先验性约束下本文算法选星后的GDOP 值相对于选星前的GDOP 值依旧没有发生太大变化,同时无论是否存在约束,选星后依旧将GDOP 控制在小于4 的范围内,满足用户精度要求,说明本文算法具有有效性。

同时基于每一历元先验性约束选星后与选星前GDOP 的差值,对其进行统计分析,如表8所示。

表8 实测数据下,选星前和先验性约束下选星后GDOP 差值在各区间下百分比Table 8 Percentage of GDOP difference before and after satellite selection with a priori constraint in each interval based on field data

与仿真情况下一致,本文将实测数据下每次选星前后GDOP 差值划为[ -0.4, -0.2),[ -0.2,0),[0,0.2),[0.2,0.4),[0.4,0.5]5 个区间,由表8可知,在实测数据下选星前后GDOP 差值有17.78%落在[ -0.2,0)区间下,说明实测数据中全部可见卫星中存在着几何构型差的卫星,从而选星后的可见卫星的卫星星座较选星前的卫星星座几何构型好,进一步说明引入可见卫星的卫星仰角和方向角先验信息后,进行先验性约束,能够在一定程度上改善选星后的可见卫星星座的几何构型。 所有的差值中最大差值依旧都小于0.5,说明选星后的GDOP 值总体上与选星前的GDOP值相差不大,在精度要求范围内。 同时,选星前后的GDOP 差值方差依旧较小,表明在实测数据下运用本文算法时,本文算法依旧比较稳定。 因此,本文算法无论仿真还是实测数据下,都具有较强的有效性。

3.2.2 实时性分析

实测数据高度截止角5°下引入先验性约束和无约束下的单次选星耗时如图8 所示,表9 为统计分析。

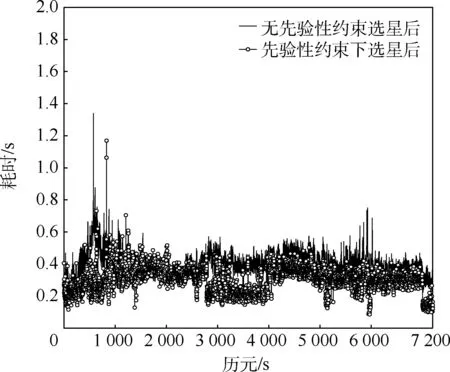
图8 实测数据下有/无先验性约束单次选星耗时Fig.8 Time consumption of one-time satellite selection with/without prior constraint based on field data

由表9 可知,本文算法单次选星实际运用时,引入先验性约束后平均耗时0.303 1 s 依旧小于无约束下的平均耗时0.400 8 s。 因此,引入先验性约束后的耗时少于无约束下的耗时,同时耗时方差较小,说明本文算法实际运用过程中,耗时稳定,在具有良好的实时性的同时仍然保持着较强的有效性。

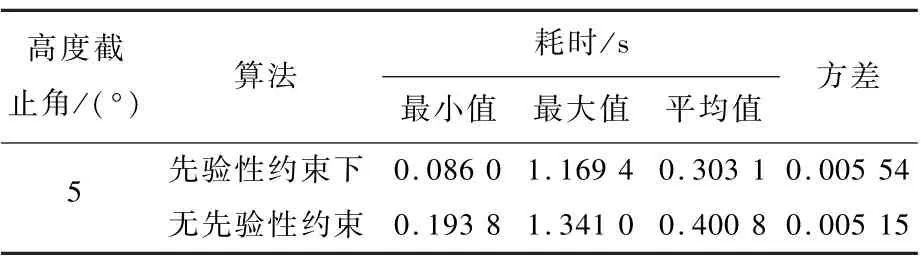
表9 实测数据下有/无先验性约束单次选星耗时数据统计Table 9 Statistics of time consumption for one-time satellite selection with/without prior constraint based on field data

4 结 论

本文设计了基于帝国竞争优化的双目标综合决策选星算法,为了选取几何构型较好的卫星星座,引入卫星仰角和卫星高度角先验信息后,进行先验性约束,同时通过构建GDOP 和选星数目这2 个目标进行综合决策实现了选星。 实验结果证明了在24 h 仿真数据和2 h 实测数据下进行先验性约束后,本文算法不仅充分降低了卫星数目,选星后依旧满足用户定位精度要求,同时选星后的GDOP 值较无约束下的GDOP 值有所减小,改善了所选卫星星座的几何构型。 24 h 仿真以及2 h实测数据验证表明如下:

1) 本文算法在24 h 仿真时间高度截止角5°下,引入先验性约束后的所选平均卫星数目近似于最大可见卫星平均数目的51.8%,同时在2 h实测数据下为总可见卫星数目平均数的52.4%,说明本文算法有效降低了卫星数目。

2) 本文算法在24 h 仿真数据以及2 h 实测数据下,引入先验性约束选星后的GDOP 值与总可见卫星数目的GDOP 值差值最大值都小于0.5,且差值方差小,说明选星前后的GDOP 差别不大,以及选星后的最大GDOP 依旧不超过4,能够满足用户定位精度要求。 因此,综合本文算法无论是仿真还是实测数据下,引入先验性约束后选星前后GDOP 变化较小以及卫星数目降低,可以说明在先验性约束下本文算法具有较强的有效性。

3) 本文算法在24 h 仿真时间下,先验性约束下单次选星平均所用时间约为0.168 4 s,相对于传统遍历法的4 s 所用时间优化了95.79%,说明本文算法具有较强的实时性。