双高箱双层集装箱运输体系弓网动力学性能研究
吕青松
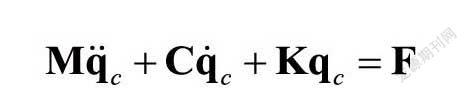



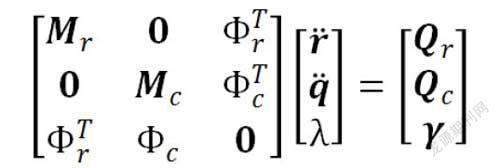




摘 要:鐵路机车车辆运行时,弓网系统的受流质量主要受到弓网系统动力学影响。双高箱双层集装箱运输体系下的接触网高度超过了现有国内接触网导线高度的最大值,以双高箱双层集装箱运输体系的试验线金甬铁路为例,接触网导线高度为6 685 mm。为了研究受电弓与在满足双高箱双层集装箱运输体系下的接触网的动力学相互作用关系,结合弓网耦合动力学分析了和谐电力机车和CRH2型车两种工况下弓网动力学性能。结果表明:机车受电弓和动车受电弓在接触导线高度为6 685 mm下,接触压力最小值和统计最小值均大于零,但随着速度的提高(从160 km/h提高至200 km/h)弓网受流质量开始恶化,标准差增大,统计最小值均小于20 N,但并未出现失压状况,弓网系统动力学和受流质量总体上满足条件要求。
关键词:受电弓;接触网;受流质量;弓网系统动力学
0 引言
近年来,我国经济发展进入新时代,全社会对铁路集装箱运输潜在需求很大,加之国家出台一系列政策鼓励促进包括集装箱和多式联运在内的快速发展,目前我国已将高速铁路、重载铁路、双高箱集装箱运输作为交通强国铁路先行的重要支撑点,从战略高度上将双高箱集装箱运输作为打造一带一路,陆港通道,江海联运的重要品牌。因此,开展双高箱集装箱运输体系研究,为我国铁路双高箱集装箱运输提供可借鉴的成果并积累可推广的经验具用重要意义。
列车运行过程中所需能量通过接触网与受电弓系统传输。通过列车上的受电弓滑板与铁路线路上的接触线的滑动接触实现接触网向列车的能量传输。从目前我国现有的技术标准和国内既有铁路接触网导线高度上来说,接触网最大高度均没有高于6 500 mm。以金甬铁路为例,接触网导线高度达到了6 685 mm。目前,国内外对于接触网导线为6 685 mm条件下的弓网动力学性能和弓网受流质量均无研究,因此,开展双高箱双层集装箱运输体系弓网动力学性能研究,为我国铁路双高箱集装箱运输提供必要的技术支持是十分必要的。
本文主要针对电力机车和动车组上的受电弓与满足双高箱双层集装箱运输体系的接触网取流时,研究影响弓网动力学性能的因素。分析电力机车和动车组两种模式下的受电弓与接触网的动力学性能,以及对弓网受流性能的影响,为铁路双高箱集装箱运输体系提供基础数据和参考依据。
1 弓网系统动力学模型
1.1 接触网模型
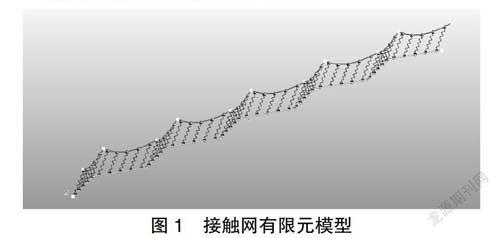
接触网模型采用有限单元法进行直接建模,接触网采用简单链型悬挂形式,通过定义接触网各部件在空间的几何位置及拓扑关系,得到其几何模型,接触线和承力索采用梁单元进行模拟,吊弦在实际工作环境中,传递的压缩力非常小,通常采用只受拉不受压的非线性弹簧单元来模拟。最后,通过对接触网的有限元划分,从而建立接触网的有限元模型,再通过有限元组装技术,得到系统的质量阵M,阻尼阵C,刚度阵K以及外载荷列阵F,从而建立接触网的运动微分方程:
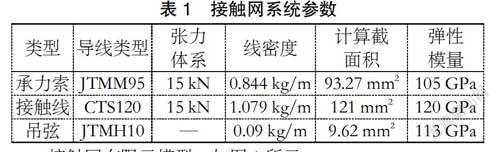
本文基于金甬铁路接触网系统的结构及参数,见表1,接触网导线高度为6 685 mm,接触网结构高度为:1 400 mm,通过在ANSYS-APDL中编制接触网有限元模型,进行单元划分,通过ANSYS的静态计算器,得到接触网的静态构型。
1.2 受电弓模型
进行弓网耦合动力学仿真时,受电弓模型通常可采用集中质量模型、多刚体模型以及刚柔混合模型等。本文采用多刚体模型进行研究,多体动力学计算软件Recurdyn基于相对坐标法开发,对于多刚体系统的计算具有计算效率和精度的优势,本文将采用Recurdyn进行受电弓多刚体建模。
1.3 弓网耦合模型
对于弓网接触问题,通常采用罚函数法进行模拟,采用线性弹簧模拟弓网间的接触刚度,受电弓与接触网之间通过接触压力耦合在一起,将受电弓与接触网的动力学方程组合在一起,构成弓网耦合系统动力学方程:
2 弓网系统动力学分析
文中主要针对CRH2型动车组及和谐电力机车上的受电弓与满足双高箱双层集装箱运输体系下的接触网(接触网导线高度6 685 mm)受流时的弓网耦合动力学进行分析,CRH2型动车组上的受电弓工作高度为2 985 mm,和谐电力机车上的受电弓工作高度为2 585 mm。
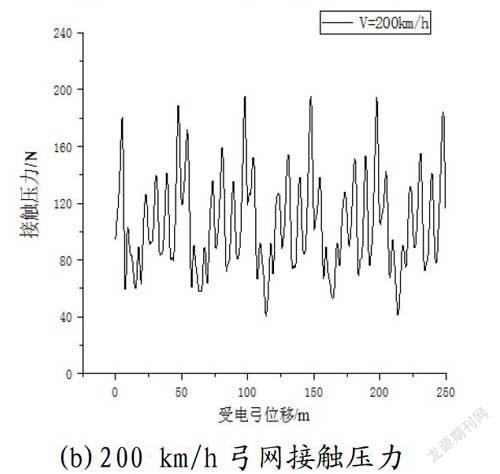
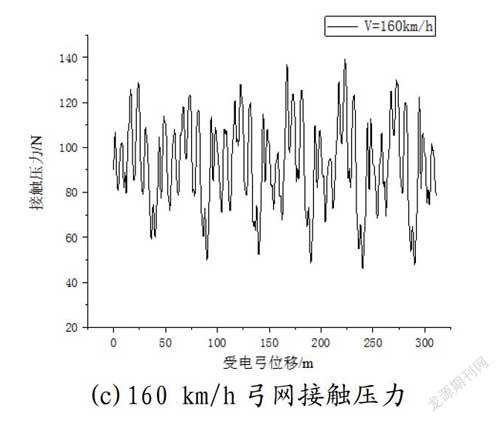
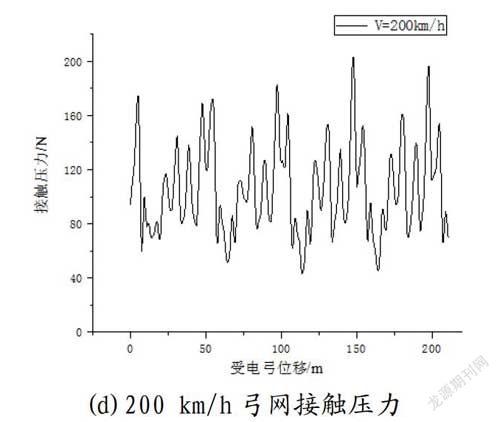
本文研究了CRH2型动车组分别在160 km/h、200 km/h
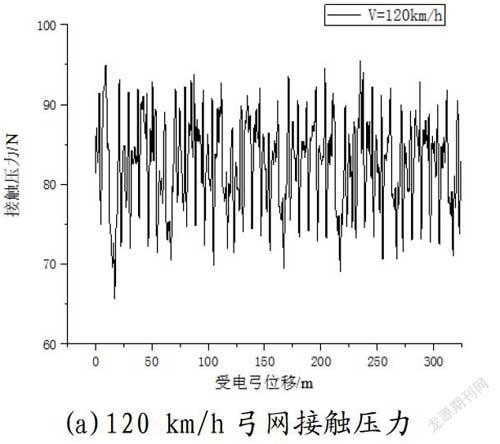
两个不同速度等级下、和谐电力机车分别在120 km/h、140 km/h、160 km/h、200 km/h四个不同速度等级下的动力学性能。
2.1 CRH2型动车组仿真研究结果
2.2 和谐电力机车仿真研究结果
2.3 接触压力统计值
对仿真工况下的接触压力进行统计,得到如表3弓网受流性能对比统计指标:
2.4 结语
从弓网耦合系统动力学计算机仿真技术研究角度分析,机车受电弓和动车受电弓在满足双高箱双层集装箱运输体系下的接触导线高度(6 685 mm),接触压力最小值和统计最小值均大于零,变异系数均大于1/3,并未出现失压状况,弓网系统动力学和受流质量总体上满足条件要求。但随着速度的提高(从160提高至200)弓网受流质量开始恶化,标准差增大。
参考文献:
[1]T.X.WU,M.J.BRENNAN.Basic Analytical Study of Pantograph-catenary System Dynamics[J].Vehicle System Dynamics:International Journal of Vehicle Mechanical and Mobility,1998(30):443-456.
[2]李丰良,李敏,唐建湘.受电弓的建模与参数测试[J]. 中南大学学报,2006,37(1):194-199.
[3]梅桂明,张卫华.受电弓/接触网系统动力学模型及特性[J].交通运输工程学报,2002,2(1):20-25.
[4]周宁,李瑞平,张卫华.基于负弛度法的接触网建模与仿真[J].交通运输工程学报,2009,9(4):28-32.
[5]张卫华,沈志云.受电弓动力学研究[J].铁道学报,1993,
15(1):23-30.
[6]ZHANG W H,MEI G M,WU X J and CHEN L Q.A study on dynamic behaviour of pantographs by using Hybrid simulation method[J].Rail and Rapid Transit,2005, 219(3):189-199.
[7]周宁,张卫华.基于受电弓弹性体模型的弓网动力学分析[J].铁道学报,2009,31(6):26-32.
[8]Ning ZHOU,Wei-hua ZHANG,Rui-ping LI.Dynamic performance of a pantograph-catenary system with the consideration of the appearance characteristics of contact surfaces[J].Journal of Zhejiang University-SCIENCE A (Applied Physics & Engineering),2011,12(12):913-920.

