基于双种群遗传粒子群算法的斜齿轮优化设计

马洪岗 刘欢 雷汶骏 马若轩 沈辉

摘要：对于多约束条件的斜齿轮传动的优化设计，提出了一种遗传粒子群算法。为尽可能的避免粒子群算法出现粒子高度聚集在最优粒子的周围的情况，采用了结合遗传算法的改进策略，并采用了双种群的进化机制。为验证所提算法有效性，实施了多种算法的仿真，仿真结果表明，相同情况下，本文所提算法能寻到更精确的解。

Abstract： A dual population genetic particle swarm optimization algorithm is proposed for the optimal design of helical gears with multiple constraints. As much as possible to avoid the particle swarm algorithm particle height gathered around the optimal particle， a combination of improved strategies of genetic algorithm is used， and dual population evolution mechanism is introduced. Secondly， in order to improve the disadvantage of the slow evolution of the ordinary genetic algorithm in the latter part of the iteration， the dual population genetic evolution mechanism was adopted. In order to verify the effectiveness of the proposed algorithm， several different algorithms are used to simulation. The simulation results show that the improved dual population genetic particle swarm algorithm can find more accurate solutions under the same conditions.

关键词：斜齿轮;粒子群;遗传;双种群

Key words： helical gear;particle swarm;genetic;dual population

中圖分类号：TP301.4                                    文献标识码：A                                  文章编号：1674-957X（2021）11-0022-03

0  引言

对于任意给定的载荷、工作环境条件、斜齿轮的几何尺寸关系和可靠性及其他制约因素，都能给出极佳的优化设计一直是齿轮传动科研人员不谢追求的目标。但由于斜齿轮设计优化问题的约束条件复杂且有大量非线性因素，因而传统的辨识算法和优化算法难以对其精确求解。现如今RV减速器作为一种常见的独立传动部件被广泛应用在工业机器人、数控装备、航天航空和医疗器械等机电一体化领域的精密减速装置中，其对斜齿轮设计也有较高要求。也正是如此，提高承载能力，延长使用寿命，减小体积和重量，一直作为设计者关注的课题。目前通用的RV减速器已有标准系列，然而其参数的配合并非最优。使用优化方法在计算机上对其进行优化设计，是在短时间内获得最佳设计结果的最有效的方法。为将智能优化算法研究的成果更好地应用于实际，本文采用遗传粒子群算法对斜齿轮优化设计问题进行求解。在Matlab平台下采用几种不同的优化算法进行对比试验，通过试验结果说明了本文给出的双种群遗传粒子群算法具有更佳的算法性能[1][2]。

1  斜齿轮优化设计的数学模型

1.1 目标函数

由于齿轮的传动比通常是根据需要预先给定的，所以由中心距和齿宽便可决定齿轮的径向尺寸和轴向尺寸。具体的目标函数如下述公式（1）所述：

式中：F（x）要尽可能的小。

1.2 约束条件

综合以满足强度要求为核心的斜齿轮传动设计方法，根据性能约束和几何约束确定以下约束条件。

1.2.1 齿面接触疲劳强度

其中：KA为工作情况系数，KV为动载系数，Kβ为载荷分布不均匀系数，Ft为圆周力，d1为分度园直径，ZH为节点系数，Zu为传动比系数，Ze为材料系数，Zε为重合度系数。由此可得下述齿面接触疲劳强度的转换约束：

1.2.2 齿根弯曲疲劳强度

其中，YF1为齿形系数，YS1为齿根应力集中系数，Yε为重合度系数。由此可得下述齿根弯曲强度的转换约束：

1.2.3 边界约束

其中，ZV为当量齿数，Ψd为宽径比。由此可得下述一系列的边界条件的转换约束：

其中，g3、g4为当量齿数约束，g5为法向模数约束，g6、g7为螺旋角约束，g8、g9为齿宽约束。

上述转换约束既要考虑了标准规范的要求，又考虑了设计、制造水平、材质好坏和使用条件等因素的影响[3]。

1.2.4 重合度

在设计中需要解决齿轮传动的平稳性问题。因此，设计中斜齿轮的重合度ε一般要求不小于2。由此可得下述重合度的转换约束：

2  改进的粒子群算法

粒子群优化算法是一种模拟鸟类捕食的高效寻优算法，由Kennedy和Eberhart于1995年提出。假定粒子群包含N个粒子，xi表示空间中的第i个粒子的位置，设Pi为第i个粒子搜寻到的最优位置，vi为第i个粒子的速度，Pg为整个粒子群的群体最优位置。可通过下式对粒子的速度和位置进行迭代：

式（9）中，i为粒子序号，;ω为惯性权重;d为粒子维度，;t为迭代次数;c1，c2为加速随机数，c1∈[0，2]，c1∈[0，2];rand为随机数，rand∈[0，1]。

采用粒子群算法容易陷入局部最优。为提升粒子群算法的全局收敛性能，本文考虑了一种将遗传进化机制引入粒子群优化算法的改进策略，以有效粒子群算法的优化性能[5]。迭代过程中，粒子群优化算法的粒子更新规则使得全部粒子总是将最优位置作为参考进行运动，从而使其具有一定的方向指引，有利于其加快寻优速度;同时，引入遗传进化机制又使得粒子群优化算法能够在陷入局部最优时不容易马上停滞寻优，会使其产生一定的扰动和变异，以增强全局收敛性能。为防止单一种群在进化后期被超级个体所统治，本文采用了双种群的进化机制。

3  仿真实验

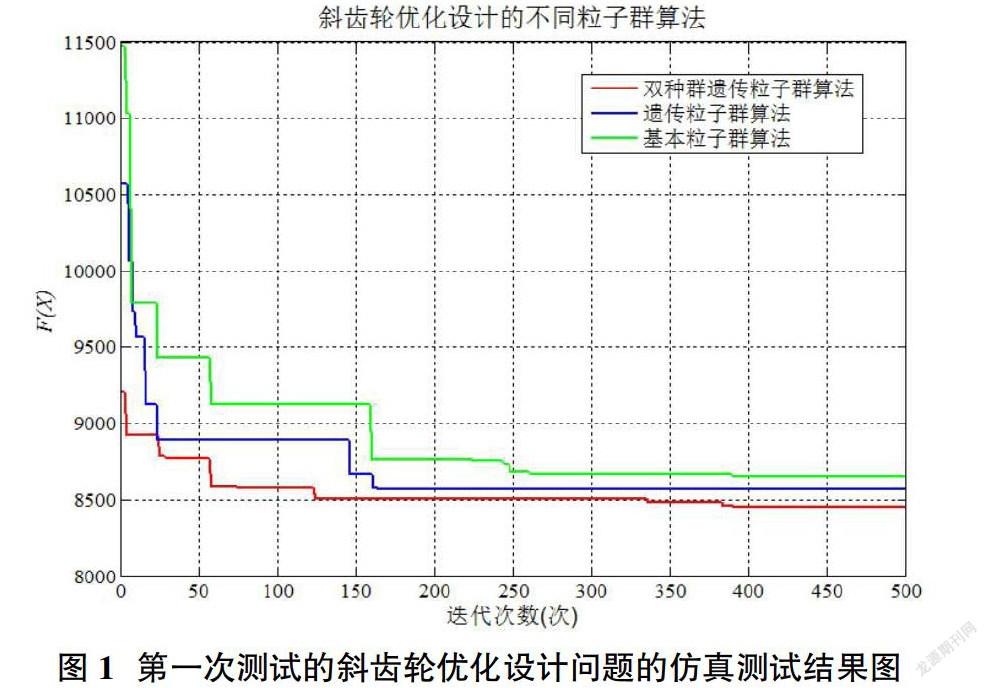
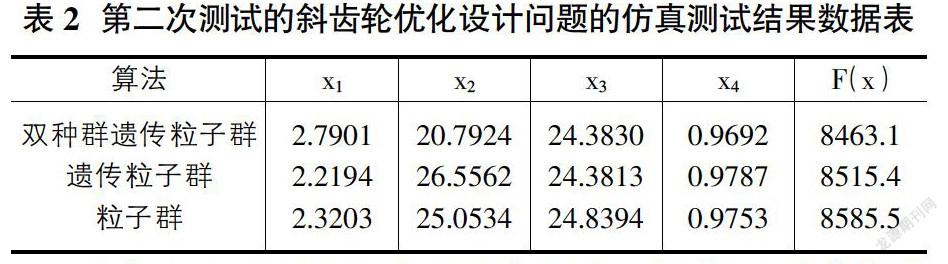
基于实际的斜齿轮设计优化问题，为验证本文提出的双种群遗传粒子群算法相较于其他粒子群算法更优。本文采用斜齿轮优化设计的实际算例对本文提出的双种群遗传粒子群算法、遗传粒子群算法和普通的粒子群算法进行两次测试。以下是具体的测试结果，如图1、表1、图2、表2所示。

由图1、图2、表1、表2给出的仿真图形和结论数据可知：本文提出的遗传粒子群算法的寻优性能更佳，寻到的目标函数值更低，因此更适合于解决实际的斜齿轮设计优化问题。

4  结论

在迭代末期，粒子群算法易于陷入局部收敛，因而不利于约束条件复杂的斜齿轮设计优化问题的求解。为此，本文提出了一种双种群遗传粒子群算法的改进策略。具体的优势如下所述：

遗传算法有助于改善粒子群算法在迭代后期多樣性损失严重的缺陷，使之在陷入局部最优时不至于立刻停滞寻优，会使其产生一定的扰动和变异，从而有助于其跳出局部最优的窘境。此外，相比于传统的单一种群进化，双种群进化机制能够更好的维护种群多样性，从而提升其全局寻优能力。

本文基于实际的斜齿轮设计优化问题进行对比实验，实验结果表明，通过遗传粒子群算法优化后的决策变量对应的目标函数值更小。因此，本文提出的遗传粒子群算法可以很好的用于斜齿轮设计优化问题的求解。

参考文献：

[1]华成丽.齿轮传动误差等价模型研究[D].重庆：重庆大学， 2013.

[2]李力行，何卫东，王秀琦，等.机器人用高精度RV传动的研究[J].大连铁道学院学报，1999，20（2）：1-3.

[3]GB/T3480-1997，渐开线圆柱直齿轮承载能力计算[S].北京：中国标准出版社，1998.

[4]曾建潮，介婧，崔志华.微粒群算法[M].北京：科学出版社，2004.

[5]杨维，李歧强.粒子群优化算法综述[J].中国工程科学，2004，6（5）：87-94.

[6]李小平，芮延年.基于灰色聚类理论斜齿圆柱齿轮传动多目标优化设计的研究[J].机械传动，2004（1）：25-27.