铝合金车轮有限元仿真分析研究
朱文婧 王永林 章孟军


摘要:车轮优化设计过程中,传统的实验分析方法周期长、费用成本高,本文采用有限元分析方法,跟据车轮实际运行状态,对车轮的弯曲试验过程构建物理模型,求解出载荷参数,通过有限元模块进行仿真分析,根据应力云图,对薄弱结构进行优化,并通过实际实验进行验证,试验结果表明有限元仿真分析在车轮优化设计过程中的有效性和可靠性。
Abstract: In the process of wheel design optimization, the traditional experimental analysis method is characteristic of cycle length and high cost. In this paper, according to the actual running state of the wheel, the physical model of the wheel bending fatigue test process is established by using the finite element analysis, and with the calculated load parameters be applied, then carries on the simulation analysis through the finite element module, optimizes the weak structure according to the stress nephogram. The analysis of the experimental results show that the finite element analysis is effective and reliable in the process of wheel design optimization.
关键词:有限元;弯曲疲劳;结构优化
Key words: finite element;bending fatigue;structure optimization
中图分类号:TP391.7 文献标识码:A 文章编号:1674-957X(2021)12-0055-02
0 引言
随着碳达峰时代的到来,节能减排对汽车工业的要求,越来越严格,整车轻量化设计已成为汽车工业设计中的重中之重。铝合金车轮作为整车的功能件和强度件,在满足机械性能的前提下,快速的质量优化已成为各大企业和众多学者研究的重要课题。
铝合金车轮的轻量化研究,就是对其结构进行优化。车轮在行驶过程中,承受来自不同方面的不规则变化作用力;同时,由于路况的多样性,增大了其复杂力学特征的研究难度。随着计算机辅助设计和有限元分析软件不断发展成熟,有限元分析成为铝合金车轮结构优化的重要手段。
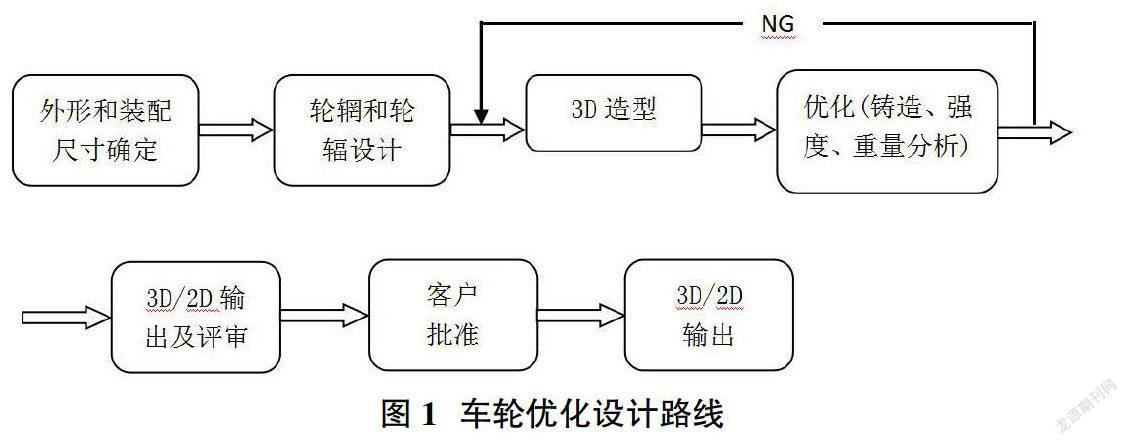
采用有限元分析方法对铝合金车轮的径向、弯曲疲劳强度进行仿真,不仅可以有效的降低实验成本,而且可以大大缩短车轮优化开发周期。通过合理数学模型建立,将参数导入有限元分析软件,靶向的模拟出车轮结构的薄弱环节,从而对不合理设计以及冗余设计进行修正,进而达到优化开发路线实现快速设计的目的,车轮优化设计路线如图1所示。本文以车轮的弯曲疲劳性能模拟为例进行分析研究。
1 模型建立
本文采用19X8.0J规格产品进行建模,19代表轮辋直径,8.0J为轮辋宽度,产品静负荷半径为342mm,偏距45mm,根据以上关键数据和造型概念,通过UG三维软件进行参数建模,最终构建三维模型。
2 建立力学模型
参照GBT 5334-2005 《乘用车车轮性能要求和试验方法》,构建固定车轮的力学模型,即对车轮其施加一个旋转的弯矩。
车辆行驶过程中,假设车轮相对于传动轴位置静止,车轮在路面和螺栓约束下,受到传动轴施加的弯曲扭矩;因此,我们可将其运动受力状态,简化为弯曲实验理论模型[1]。根据弯曲实验理论模型我们可得车轮的弯曲扭矩公式(1):
根据标准,轮胎与路面的摩擦系数?滋取0.7,静负荷半径R为342mm,强化系数取推荐值1.6,轮辋的偏距d取45mm,从而可得弯曲扭矩M为4103N.mm。
又因,弯矩与实验载荷间的关系:
故取加载轴L长度为660mm,可得实验载荷:
在实际行驶过程中,车轮是不断转动的,所以实验过程中,施加与轴上的载荷方向也是随着时间变化的;为了保证作用于轴上力的大小不变,我们可以将力F分解为x轴和y轴两个方向[2]。设时间变量为t,车轮转动角速度为?棕,则可以得到任意时刻x轴和y轴上的分作用力Fx=sin ?棕t和Fy=cos ?棕t,实验过程中,设定车轮的转速n=750r/min,则在轴端的加载力周期T=1/n=0.08s;如果将车轮一周360°等分为30个方向,将载荷离散的分别加载在这30个方向上,将时间t设为1-30的整数,可求得每次加载力的大小。
3 弯曲疲劳强度有限元分析
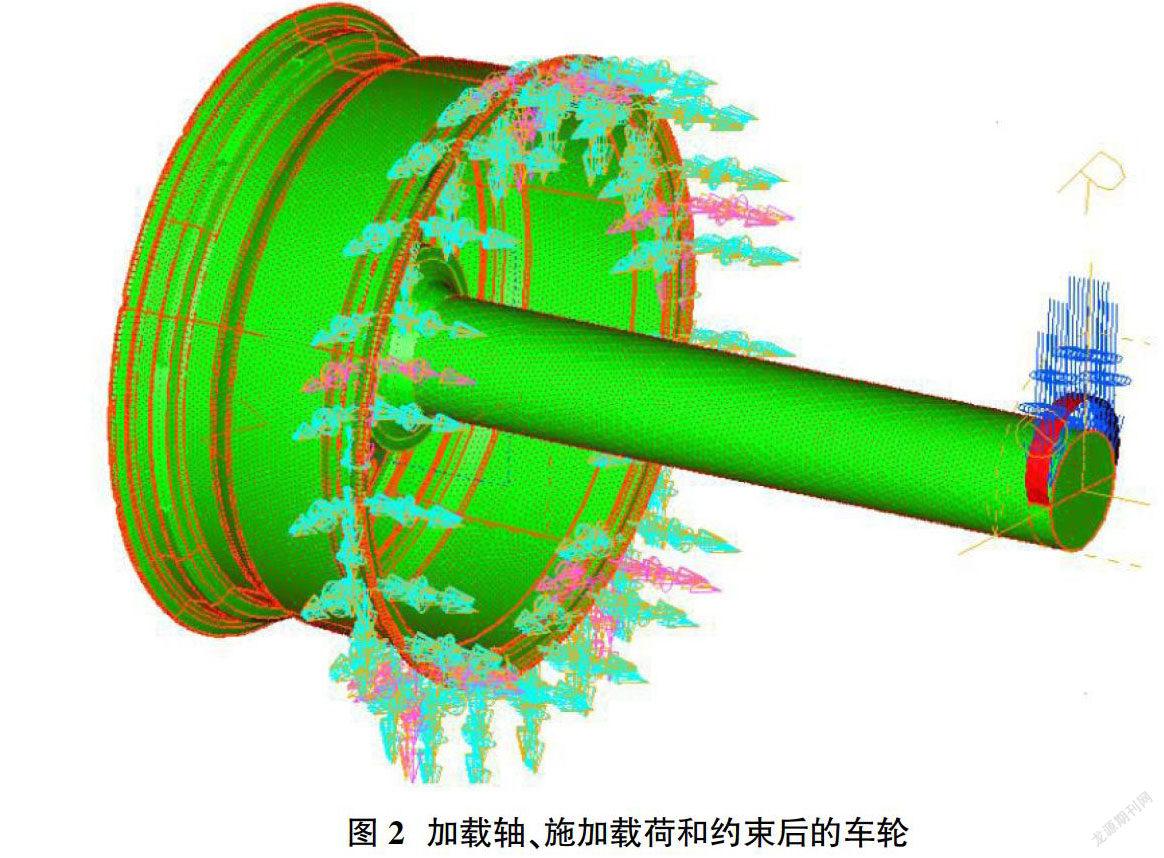
①本文采用IDEAS分析软件进行有限元分析,将UG中建好的车轮模型导入IDEAS,在软件中建立连接盘和加载轴,链接盘直径设为180mm,高度为60mm,加载轴的直徑和高度分别为100mm和600mm,如图2所示。
②网格划分。理论上网格越密,有限元单元越多越接近实际值,但不可避免的增大了运算量,延长了分析时间[5-6];在既能保障精度,又不至于花费太多的运算时间,本文采用四边面网格,网格密度为8;选择材料的弹性模量E为71000MPa,泊松比为0.33,材料密度为2.69g/cm3。
③施加载荷和约束。在加载轴的远端创建载荷施加面,将上文计算好的作用力施加于载荷面上;实际实验中,车轮通过螺栓固定在实验台上,夹具将轮缘固定,车轮的2个转动自由度和3个移动自由度完全被约束,只有车轮绕加载轴的转动自由度允许存在;本文参照实际情况,由于建模时车轮与加载轴已经紧固链接,所以只需对轮缘施加约束载荷,即可实现车轮只有一个转动自由度。施加后约束后的结果如图2所示。
④运算求解。将约束和载荷建立联系,导入求解器求解结果,最大应力集中处应力云图如图3所示。
根據弯曲应力云图,可以得出,正面造型面的应力集中主要出现在车亮面与铸造面阶梯平台的圆角处,此处圆角较小,车亮面凸起较窄,容易造成应力集中,与实际情况相符,在优化设计中,可以考虑优化该处的圆角;分析背面弯曲应力云图,应力集中在大窗口拐角处,应力值为114MPa,虽远没有达到铝合金的最大屈服许用应力,但是超过实验经验破坏值110MPa,此处的结构设计存在着风险,在实际设计中,应考虑对该处的结构进行调整。
4 实验验证
将试制样轮固定于弯曲疲劳试验机上,表面喷涂探伤粉,根据第二节数据设置实验参数,实验后载荷循环180万次,未见明显裂纹,继续进行做极限实验,最终得到疲劳裂纹,实验发现轮辋大窗口拐角处最先出现疲劳裂纹,这和上文的仿真结果,基本一致,从而证明了有限元仿真的有效性。
5 结论
①施加于加载轴的弯曲载荷在试验过程为余弦方式加载,其大小不变,方向随时间变化。②车轮与轮胎接触部分的应力采用余弦函数的方式进行加载,从车轮中线至大约逐渐减小。③通过实验验证,仿真应力集中位置和实验疲劳裂纹出现位置一致,仿真分析在应力模拟分析中具有可靠性。
参考文献:
[1]单萍.铝合金车轮动态有限元分析及优化设计[D].山东建筑大学,2020.
[2]赵铁石.锻造铝合金商用车车轮的设计仿真与开发[D].燕山大学,2017.
[3]杨云端.某轿车铝合金车轮疲劳分析[D].南京理工大学,2018.
[4]王一浏.车轮结构-材料一体化轻量化多目标优化研究[D].吉林大学,2016.

