公路平曲线加宽及其过渡方式浅析
江强兴






摘 要:本文从提高公路行车安全、减少路面病害的角度出发对公路平曲线加宽及其过渡方式提出了分车道加宽和四次抛物线过渡,虽然计算更麻烦一些但能使平曲线更加协调、顺适,驾驶人员更易遵循路线行驶,提高了车辆行驶的安全性和舒适性。
关键词:分车道加宽;四次抛物线;过渡方式
0 引言
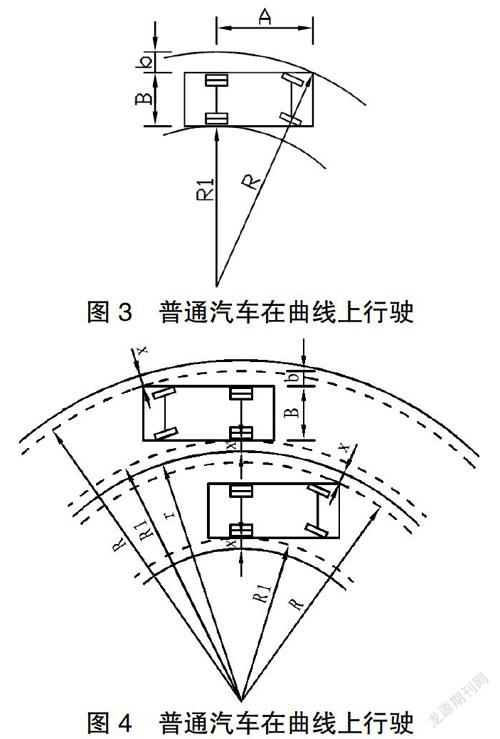
汽车行驶在曲线上,前后轮会划过不同的曲线轮迹,各轮迹半径不同,其中以后内轮轨迹半径最小,且偏向曲线内侧,同时车辆一定转速的前轴操纵使车身也存在一定的摆幅,故曲线内侧应增加路面宽度,给车辆转弯提供合理的空间,以确保曲线上行车的顺适与安全。
根据《公路路线设计规范》二级公路、三级公路 、四级公路的圆曲线半径小于或等于 250 m时,应设置加宽。圆曲线上的路面加宽应设置在圆曲线的内侧,各级公器的路面加宽后,路基也应加宽。双车道公路在采取强制性措施实行分向行驶的路段,其圆曲线半径较小时,内侧车道的加宽值应大于外侧车道的加宽值,设计时应通过计算分别确定。公路采用强制性措施实行分向行驶的比较少见,一般双车道路面的平曲线均采用内侧加宽的方式,如下图1、图2所示,存在着以下缺点:
(1)混凝土路面施工时按設计中线放样,交通标线施工一般按照纵缝施工。路面双车道的加宽值都加在曲线内侧车道,内侧车道就太宽造成了浪费,当采用一个板块时增加了混凝土板应力,使路面出现纵向裂缝病害。曲线外侧车道没有加宽,满足不了汽车行驶的宽度要求,车辆往往跨线行驶,违反了交通规则,增加了安全隐患。
(2)路面的几何中心偏离了路线设计中线,实际路中线偏向内侧,在缓圆和圆缓二点曲率不连续。
1 加宽值的方法和计算
为克服以上缺点,本文参照强制性措施实行分向行驶的路段加宽规定,提出双车道路面平曲线加宽均实行分车道加宽,内侧车道向内侧加宽,外侧车道向外侧加宽,具体分析如下:
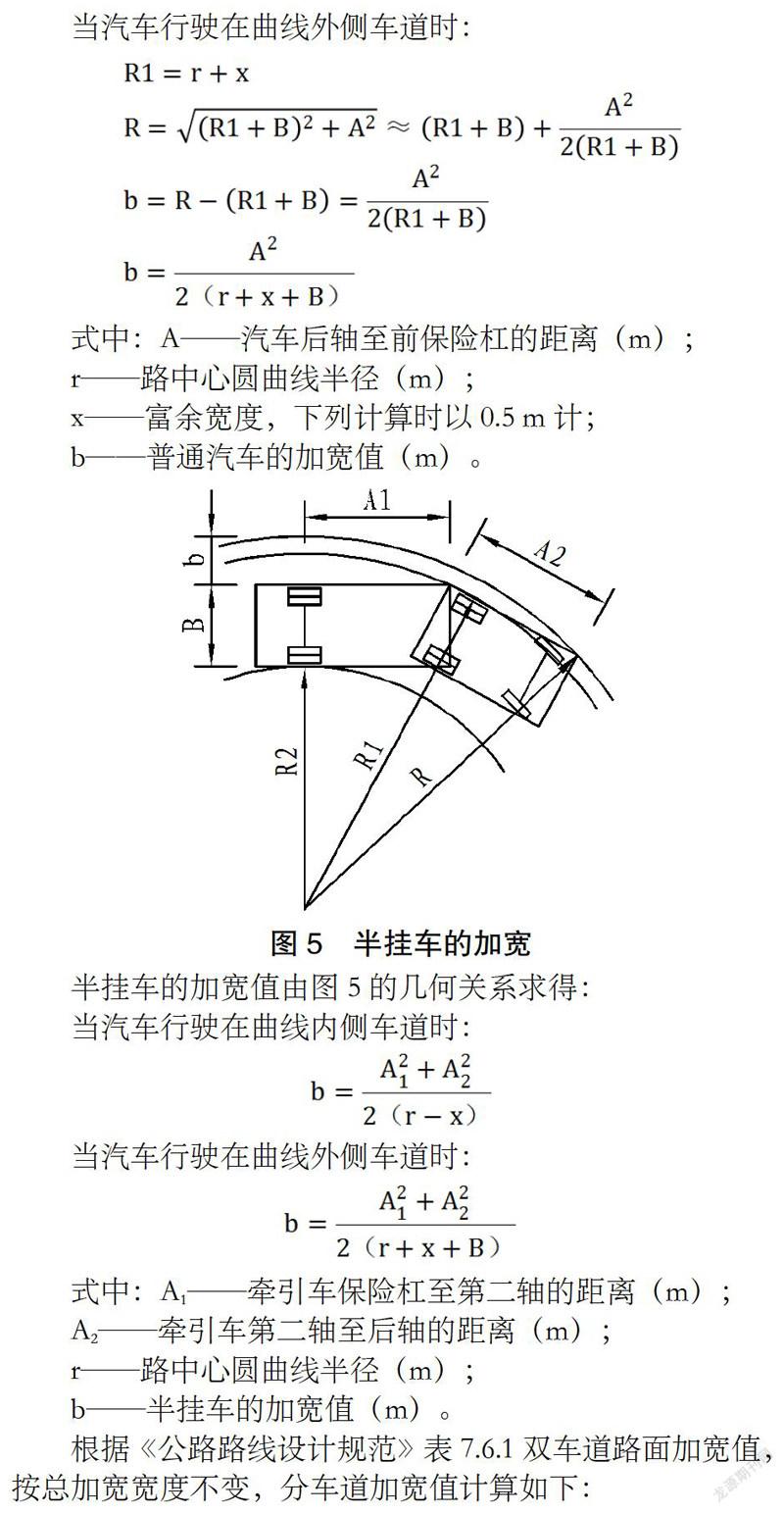
普通汽车行驶在曲线上如图3、图4所示:
当汽车行驶在曲线内侧车道时:
当汽车行驶在曲线外侧车道时:
式中:A——汽车后轴至前保险杠的距离(m);
r——路中心圆曲线半径(m);
x——富余宽度,下列计算时以0.5 m计;
b——普通汽车的加宽值(m)。
半挂车的加宽值由图5的几何关系求得:
当汽车行驶在曲线内侧车道时:
当汽车行驶在曲线外侧车道时:
式中:A1——牵引车保险杠至第二轴的距离(m);
A2——牵引车第二轴至后轴的距离(m);
r——路中心圆曲线半径(m);
b——半挂车的加宽值(m)。
根据《公路路线设计规范》表7.6.1双车道路面加宽值,按总加宽宽度不变,分车道加宽值计算如下:
2 加宽的过渡
根据《公路路线设计规范》规定:设置回旋线或超高过渡段时,加宽过渡段应采用与回旋线或超高过渡段长度相同的数值。
双车道路面加宽过渡段的过渡方式主要有两种,一种是采用长度成比例增加的比例渐变方式,一种是采用四次抛物线渐变方式,列出计算公式如下:
比例渐变方式:
四次抛物线渐变的方式:
式中:——任意桩号位置(任意点)距加宽过渡段起点的距离(m);
——加宽过渡段的长度(m);
b ——圆曲线上的全加宽值(m);
——任意桩号位置(任意点)的加宽值(m)。
内侧车道向内侧加宽,比例过渡简单易作,但经加宽以后的路面内侧与行车轨迹不符,缓和段的起终点出现破折,于路容也不美观;四次抛物线过渡的路面内侧边缘圆滑、美观。外侧车道加宽时是向外加宽,加宽后边线会不会向外侧凸出呢。根据回旋线切线支距法公式,曲线上该点的外侧加宽值大于支距y时外侧边线向外凸出。
比例过渡:
四次抛物线过渡:
式中:——任意桩号位置(任意点)加宽值与支距y的差值(m)。
由上式可得:比例过渡当时外侧车道边线向外侧凸出;四次抛物线过渡时由于公式比较复杂,较难判断外侧车道边线是否会向外凸出,采用穷举法进行试算,发现是否向外凸出与曲线半径、全加宽值和回旋线长度有关,一般情况下外侧车道边线不向外凸出或凸出数值较小,不影响驾驶员正确判断和行驶。推荐外侧车道加宽过渡采用四次抛物线,为使内外一致,建议内外侧均采用四次抛物线过渡。
汽车行驶在曲线上,前后轮会划过不同的曲线轮迹,各轮迹半径不同,其中以后内轮轨迹半径最小,且偏向曲线内侧。在双车道路面上汽车末超车行驶时应各行其道,内侧车道的汽车前保险杠外侧沿路中线行驶在曲线起点处开始转弯,其后内轮同步偏转进入曲线,即后内轮提前A米距离进入曲线,因此内侧加宽应提前A米开始加宽,A值为汽车后轴至前保险杠的距离,不通行或较少通行铰接客车和铰接列车可取整为10 m,通行铰接客车和铰接列车时可取为15 m。外侧车道则相反,后内轮曲线起点处开始转弯,汽车前保险杠已进入曲线,即汽车延迟A米才开始转弯,与外侧车道向外加宽相吻合,不需要延迟处理,考虑到外侧车道延迟转弯,建议小半径曲线时采用较大的缓和曲线长度。
当线型为S形或C形时内侧车道提前加宽后,前后二个曲线对提前加宽段都有一个加宽值;提前加宽段上任意点的加宽值如何计算,经不同线型组合试绘后,得出叠加的方法,如下式:
式中:——任意桩号位置(任意点)的总加宽值(m)。
——任意桩号位置(任意点)的前曲线加宽值(m)。
——任意桩号位置(任意点)的后曲线加宽值(m)。
3 加宽的面积
四次抛物线加宽过渡段的加宽值为四次抛物线变化,其加宽面积采用定积分计算:
求原函数:
当等于时,加宽过渡段加宽的面积:
式中:——任意桩号位置(任意点)距加宽过渡段起点的距离(m);
——加宽过渡段的长度(m);
b ——圆曲线上的全加宽值(m);
——任意桩号位置(任意点)的加宽值(m)。
4 结语
路线设计是公路建设中的“灵魂”部分,平曲线加宽是路线设计的一部分,分车道加宽和四次抛物线过渡虽然计算更麻烦一些但能使平曲线更加协调、顺适,驾驶人员更易遵循各自的车道而不跨越车道行驶,提高了车辆行驶的安全性和舒适性。
参考文献:
[1]彭飞,杨帆.平曲线加宽后内侧边线和中线方程的研究[J].工程图学学报,2007,28(6):107-113.
[2]彭绍勇,吴华金.高速公路平曲线加宽的方法[J].云南交通科技,1998(1):28-31.

