基于遗传算法管制员岗位排班
张旭






摘要:排班问题是一个重要的组合优化问题[2],每种特定情况下的排班都有各自不同的解决手段。本文在考虑到管制员排班过程中的各种限制条件的情况下提出一种基于排班时长公平性的遗传算法[4]管制员排班模型。经过实验改进算法程序能够在几分中之内得出一个周期内的具体排班。
一、管制员排班的特点
在民航系统中,管制员是守护安全的第一线人员,由于岗位的特殊性,他的岗位排班与人员的资质直接相关,在现场运行过程中由于人员的资质不相同,相应的个人排班代码也不尽相同(如领班代码只能由具有领班资质的人值守)。随着各种限制要求的增加,人工排班过程中不时会出现顾此失彼的情况,本文综合上述考虑,从人员搭配,人员资质,平均时长,特定日期代码需求,上下半夜教员排班五个方面着手建立遗传算法排班模型。
二、管制员排班模型
2.1 排班限制条件分析
日常排班过程中,首先要考虑的是管制员的资质问题,现有参与排班的管制员资质大致如下:领班,教员,管制员,新放单管制员,部分放单管制员。每种资质所对应的代码集合都不一样,在实际排班中用不同的代码字符表示。人员特定日期的代码需求可以预先在代码表中体现出来,此过程体现在预排班中。每类资质人员的排班代码和人员搭配有不同的要求。本文主要的排班目标为,整体管制员工作小时数最平均,尽量避免连续大夜,满足上下半夜均有教员,满足资质搭配要求,满足个人的轮空需求这五个方面进行排班,求解多目标条件下的极值[3]。
算法模型
其中表示相应的权重系数,fs表示小时数的方差,fn表示连续大夜的罚值函数,fp表示满足人员代码需求的罚值函数,fj表示满足上下半夜教员排班的罚值函数,fm表示人员资质搭配的罚值函数。
其中表示每个人的排班周期内的小时数总数,表示排班的周期内的平均小时数。
其中表示第i为管制员的相邻两个代码,为判断函数,若果为两个连续大夜则返回1,否则为0。
其中分别为排班表和特定需求表,为判断函数,如果ScheduleTable里面特定 位置的与Personneeds中相应位置的相同则返回0,否则返回1。
其中表示教员资格的人数,分别表示第i时段的教员代码集合,上半夜代码集合,下半夜代码集合。为判断函数,如果Gi中的代码既在patternS里面又在patternX里面则表示上下半夜都有教员,则返回1,否则返回0。
其中分别表示不能搭配的人员的代码对集合和排班代码中相互搭配的代码对集合。为判断函数,如果在中则返回1,否则为返回0。
对于遗传算法函数的松弛函数的确定,通过
综上所述:整体基于遗传算法的管制员排班模型为下:
2.2 算法复杂性分析
根据排列组合原理计算可以得到,N位排班人员在T周期之内排班的解空间大小为,从中可以看出随着排班周期和人数的增加解空间的大小呈指数增加,传统的算法很难在有限的时间内求得满意解,因此选择启发式算法。根据遗传算法的特点,本文针对管制员算法的特定,设计了相关的遗传算法。算法能够在5分中之内求得满足条件的满意解,大大减少了排班的人力成本 。通过跟现场的各个小组的排班人员的调查分析了解到。正常情况下制订一个有特定需求的排班,平均需要花费1~2小时,有时候甚至需要更长的时间。并且由于口算的局限性,很难保证同时满足多个限制条件。
2.3 遗传算法设计
考虑到排班过程中,每天的代码都是相同的,所以每个在产生初始种群的过程中,我们根据实际的排班要求随机产生每天的排班,也就是排班表中的一列的数据(遗传基因),然后通过循环来产生一个周期内的排班表(染色体)。在常规的遗传算法的运算过程中,交叉操作是为了产生新的优良的个体,变异操作是为了防止算法过早的陷入局部最优解。一旦在初始种群确定之后,整个种群的基因就基本上是确定的了,交叉操作并不能保证整个搜索的遍历性,因此本文中,变异也作为产生新个体的一个重要的手段,因此在本文中设置的变异概率要远远大于常规遗传算法的变异概率。
产生初始种群,本文将每一个可能的排班表作为一个遗传父本。
其中表示第i个人第j时段的代码。
关于遗传算法的设计的基础知识在[1]已经有较为详细的描述,本文采用类似的遗传算法编码方法。本文直接将每个排班表作为父本,进行算法操作。算法交叉操作
本文采用两点交叉法。为了能够使得遗传向着较好的方向进行,更快地逼近最优解。在算法运算过程中再加入一些特殊的点交叉具体过程如下图
变异过程示意图:
算法分析:
根据每个系数的设置我们可以看出适应度函数值的跨度比较大。从1000~10。这样在遗传算法的执行过程中,很可能会使得函数过早地陷入局部最优解。因此在算法在执行过程中有很大的可能性较早的陷入局部最优解。因此,本文在算法执行过程中设置了一个操纵算法——伪变异过程。在计算过程中将小时数最多的人的一个大夜代码与小时数最少的对应位置的代码互换。如图所示
为了能够较好地,较全面地搜索到最优解,设置变异地概率在50%以上。
算法检验
在本算法设计过程中,产生新的遗传个体的产生并不是主要通过交叉过程获得,而是通过随机的变异过程来获得。因此实验中变异的概率要设置在50%以上,才能很好的保证算法的遍历性。
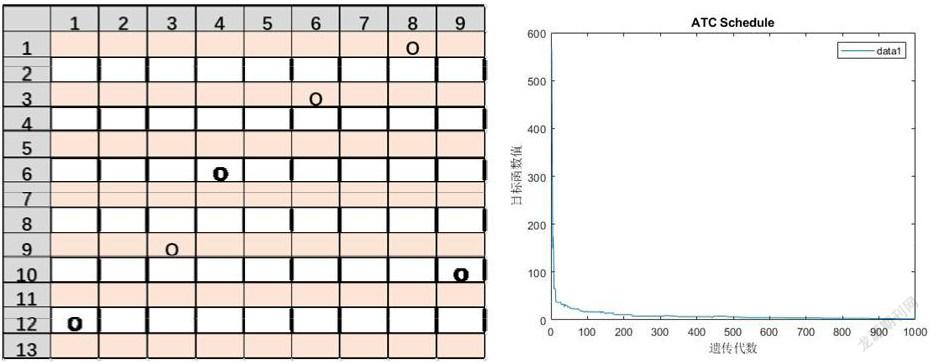
上图是一个预排班表,列表示排班周期为9,排班人数为13人。字符O表示人员的代码需求,实际排班中表示轮空代码,不能搭配人员序号组合为[9 13;7 13]。右侧为算法排班结果,本次实验用时178秒。
三、分析与展望
虽然本文针对具体的管制员排班进行分析,但是文中所提到的编码手段对于此类排班都是有效的,通过适当方式的编程方式能够实现在一分钟之内就能得到较满意的解。罚值函数的确定和罚值函数系数的确定是遗传算法能否有效搜索的重要条件。文中所给出的系数都是通过参考罚值函数的值,然后预估一个较合适的系数,再通过多次试验不断改进得出的,并没有确定罚值函数系数的计算公式,这是在未来研究的一个方向,如果能够确定准确的罚值函数系数组合,那么算法的收敛速度和搜索的精度就会大大的提高,排班结果也会更好。
参考文献:
[1] 武广号, 文毅, 乐美峰. 遗传算法及其应用[J]. 应用力学学报, 2000, 23(6):9-10.
[2] 孙宏. "航空公司飞机排班问题:模型及算法研究." 西南交通大学, 2003.
[3] 胡毓达. 实用多目标最优化[M]. 上海科学技术出版社, 1990.
[4] https://baike.baidu.com/item/%E9%81%97%E4%BC%A0%E7%AE%97%E6%B3
(民航局運行监控中心 北京 100010)

