巧用分类思想来解决面积重合问题

摘 要：初中数学教学中，要帮助学生学会利用八种分类方法计算面积重合问题.在“数学模型→绘出图形→文字描述→符号表达”抽象化的一系列过程中，提高学生顺向、逆向相互转化的思维能力，让学生立足于基础知识，加强知识间横向与纵向、内在与外在、具象与抽象之间的联系.

关键词：分类计算;图形运动

中图分类号：G632文献标识码：A文章编号：1008-0333（2021）11-0002-02

作者简介：侯坤明（1980.4-），男，江蘇省灌云人，本科，中学一级教师，从事中学数学教学研究.

几何图形的运动变化问题一直以来都是中考命题专家青睐的热点，这一类题目在编写时都不同程度上体现出基本图形、基本概念来源于现实生活，将现实生活中的一些问题抽象化得到.这类题型注重培养学生良好的观察、操作、想象、讨论、交流等学习习惯，学生在吸收知识的同时更能够领悟其中蕴含的基本数学思想，并通过适度的提炼和总结，使之能对认识能力、理解能力和应用能力起到指导作用，更好的理解数学实质，初步获得数学思维能力.

笔者在给学生讲解苏教版八年级下学期第95页的第22题时，受到了一些启发.原题如下：

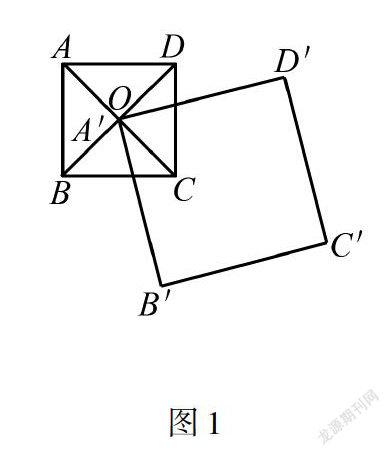
如图1，正方形ABCD的对角线AC、BD相交于点O，正方形A′B′C′D′的顶点A′与点O重合，将正方形A′B′C′D′绕点A′旋转，在这个过程中，这两个正方形重合部分的面积会发生变化吗？证明你的结论.

我们将上题中的两个正方形都变为：

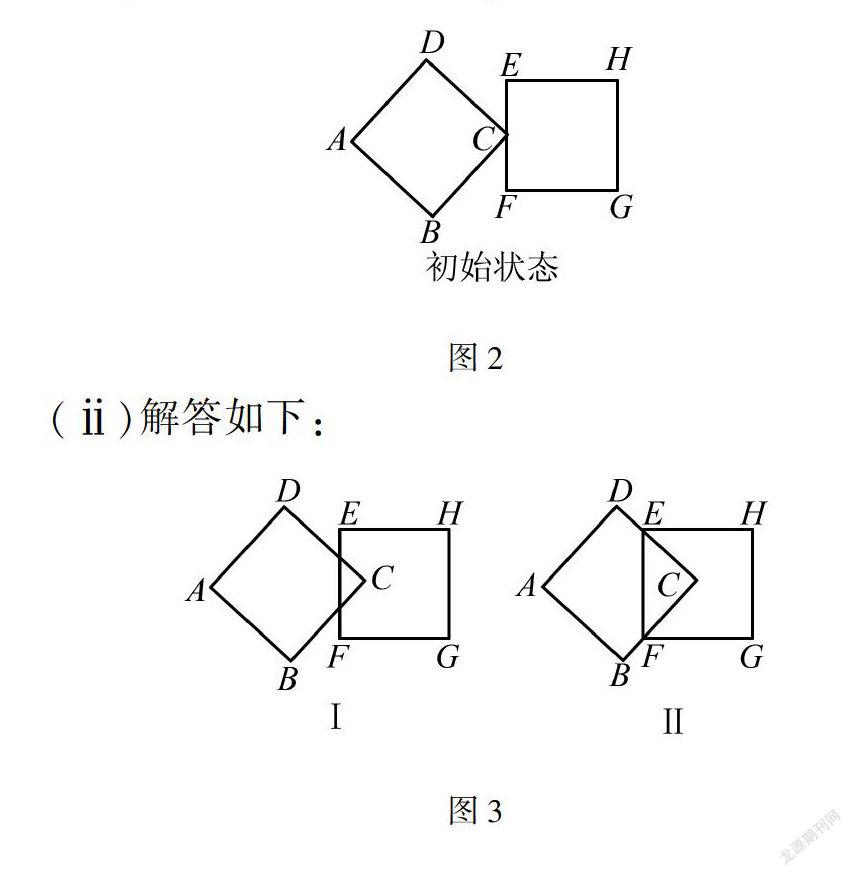
边长为6的相同正方形，按如图2所示方式放置，右边正方形EFGH是水平放置的，其中∠BCF=45°，C是EF的中点（左边正方形的右边顶点与右边正方形的边所在的中点重合），同时令左边正方形水平向右按每秒钟一个单位长度平移，右边正方形EFGH固定不动.请你尝试解决以下问题：

（1）在运动过程中BC与FG的夹角等于度;

（2）当t=2时，求正方形ABCD余下的面积;

（3）请你计算从左边正方形ABCD开始进入直至完全穿过并离开右边正方形EFGH时，两正方形重合部分的面积s与运动时间t（初始状态时t=0秒）之间的函数关系，并求出对应的t的取值范围.

（4）在（3）的情况下有无重合面积的最大值，若有请求出来;若没有，请说明理由.

解 （1）45°（135°）;（2）32;

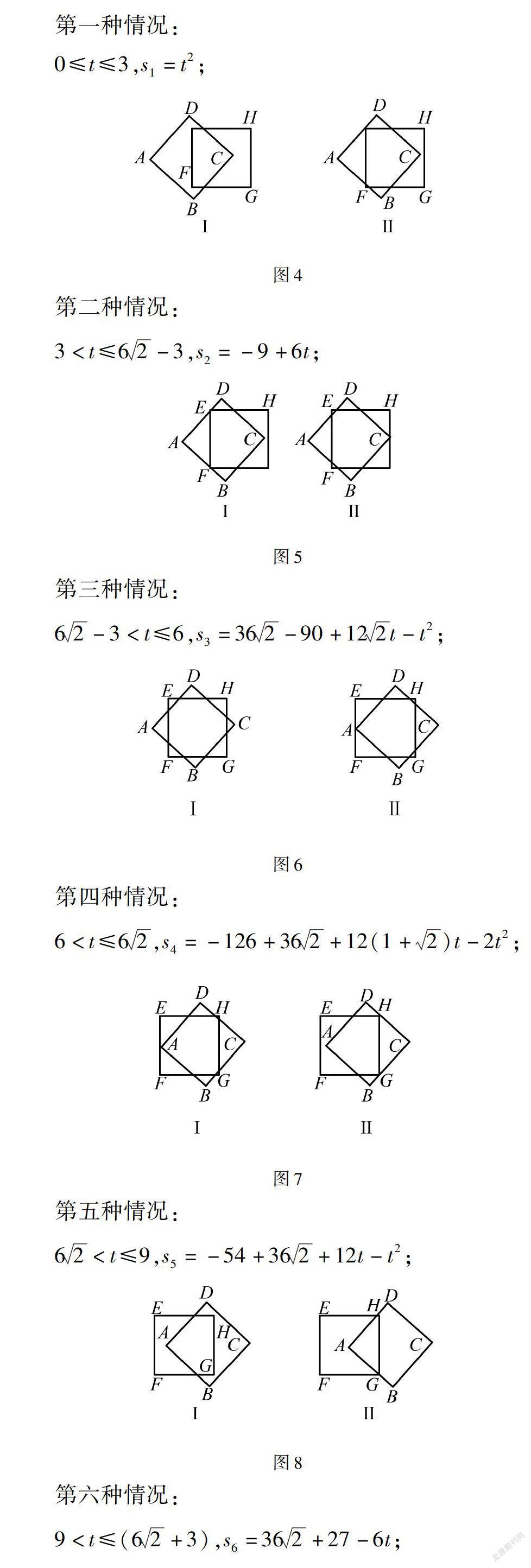
（3）（ⅰ）分析：首先呈现移动变化过程中的关键位置的系列图，然后根据重合部分形成的多边形的边数划分为八种不同的情况.每一种情况分别分为两个状态图，即进行状态和结束时的临界状态，并分别计算此种情况下它们重合部分的面积与运动时间t（初始状态时t=0秒）之间的函数关系.

从第一种情形到第八种情形的解答全部过程，明确的反映出了从正方形ABCD开始进入直至完全穿过并离开正方形EFGH时，两正方形重合部分的面积与运动时间t（初始状态时t=0秒）之间的函数关系.从上述图形的运动过程可以看出，重叠部分的图形经历了三角形→五边形→七边形→八边形→七边形→五边形→三角形这一循环往复过程，但重合部分的面积表达式却截然不同，其中原因是时间t的取值变化之后，重合部分的面积求法就大相径庭，不能用前面相同图形的面积随意代替后面的.在计算每一种情况下图形的面积时，需要把不规则的图形切割成规则的图形，计算虽然困难，但只要抓住正方形的边长a、对角线2a始终保持不变以及运动时间t，灵活应用直角三角形的性质、函数思想等知识，就能较快的计算出重合部分的面积.

参考文献：

[1]骆奥，李雪.浅谈体育教学中小组长的作用[J].群文天地，2010（006）：167-168.

[2]张国华.捧着一颗心来 不带半根草去——人民教育家陶行知[M].吉林：吉林人民出版社，2011：56-60.

[3]杨裕前，董林伟.数学 八年级下册[M].南京：江苏科学技术出版社，2013：6-10.

[责任编辑：李 璟]