初中数学中"最短路径问题"的探究
张凯
摘要:数学课是全部初中教育管理体系中十分关键的构成部分,因而提升对其科学研究针对学生来讲十分的关键。数学初中最短路径这个问题是数学课知识中的一个关键难点,其可以充足地反映数学课知识来自日常生活。最短路径难题可以分成平面图形展开图中的最短路径难题、点与点中间的最短路径难题及其点和线中间的最短路径难题。而文中关键便是对于数学初中最短路径难题的研究和拓宽开展了详尽的剖析,期待可以对同行业有一定的启示。
关键词:数学初中,最短路径;研究;拓宽
中图分类号:TU 文献标识码:A 文章编号:(2021)-07-233
前言:新课标中清晰地强调,数学初中课堂教学不仅必须让学生把握有关的数学课基础理论,而且还得从实践活动研究的视角来塑造学生的数学课知识运用的能力,从而合理地提高学生的创新精神、探索观念及其全局觀念。在传统式数学初中的教学环节中,老师一般全是有理有据地开展课堂教学,而针对知识和日常生活中间的训练就比较忽略了,那样可能促使学生在具体的学习过程中只可以简易的牢记某一类练习题的答法和有关的基础理论内容,而不能够深层次的掌握到数学课基础理论的实质,因此中学数学老师务必得积极主动地去调节。
1、初中数学中“最短路径难题”的研究现况
依据新课标的规定,数学初中课堂教学不但要让学生掌握基本上的数学课基础理论,还应当从实践活动研究的视角对学生的知识 运用能力开展塑造,进而慢慢提高学生的全局观念、探索意识和创新精神。在传统式数学教学中,老师习惯有理有据地解读知识,而忽略了知识与日常生活的训练,那样学生在学习中通常只有记牢基础理论内容或某一类练习题的答法,而无法透过练习题,研究数学课基础理论的实质,在新课改中,老师应当对于这样的课堂教学情况做出调节,从实践活动与探索的视角对学生的知识应用能力明确提出新规定,并设计新的教学方案。“途径最短难题” 是数学初中环节一个关键的种类题,另外也是一个与实际生活联络紧密的基础理论内容,在课堂教学中,老师能够根据“大将饮马难题”“堤岸修桥难题”引起学生的思索,从而深层次探究难题的基础理论原动力。
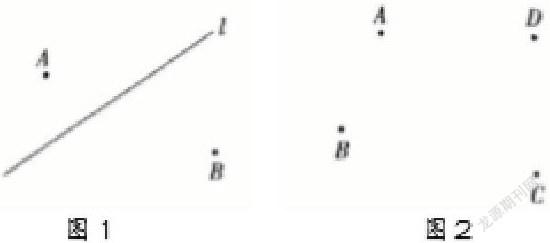
2、难题导进,激发现有知识难题的导进是教学课堂的第一步,在最短路径课堂教学中,老师为学生提供了下列2个疑难问题:难题 1:如图所示 1 所显示,某条道路 l 沿岸两边有两个货运物流转运站 A 和 B,某公司观念在铁路沿线创建一个物流配送站,我想问一下将地址挑选哪儿可以确保该地址到 A.B 两个地方的间距之和最短。
难题 2:某镇子有四个行政村 A.B.C.D,其遍布如图所示 2,
镇政府为减轻各乡的自来水焦虑不安难题,方案项目投资基本建设 一个贮水池,我想问一下贮水池应当怎样开店选址才可以确保其道各乡中间的间距之和最少?这两个难题既是日常生活普遍的,也是数学习题中普遍的,学生根据立意剖析,能够从这当中发觉“两点之间直线最短”这一基本理论的案件线索,从而激发已学的知识和现有的答题经验,一此为搞好课堂学习埋下伏笔。
3、互动交流研究,提升协作能力
针对中学生来讲,学生的综合性能力塑造不但可以确保其知识学习效果,还可以确保其知识探索的主动性。课堂教学互动交流是活跃课堂教学气氛,塑造学生互动交流观念和协作能力的重要,在最短路径课堂教学中,老师能够根据课堂教学难题,为学生设定课堂教学每日任务,并推动学生进行协作。
4、推进学习培训,加强知识了解
工作布局是回望课堂教学,推进新知识的关键方式,在课堂教学中,老师能够利用某一类的题目对学生明确提出规定,进而正确引导学生慢慢推进对知识地了解。如某老师在工作分配中为学生出了那样一道题型:A.B 两个地方在一条河的海峡两岸,现要在河岸建一座桥 ,怎样修桥才可以使得A到B的途径最短?在答题中学生能够自主绘图将具体难题抽象成数学题目,在这里的题型中,公路桥梁自身的长短也必须考虑进去,因而,学生在审题中,应当先连接A 点与 B 点同一平行线上的点 E,再一次衡量两点之间直线最少的难题,随后再利用平移变换,在江河上找出公路桥梁的平行面部位,并利用“三角形的两边之和超过第三边”的定律开展思考,进而明确公路桥梁部位。在工作布局中,老师既要联系课堂教学上的内容,还应当适度更改已经知道标准,提升题目难度系数,以推动学生发展。
5、难题课堂教学,逻辑思维的原动力驱动力
难题课堂教学是启迪学生逻辑思维的原动力驱动力。以难题为关键的课堂教学,是根据正确引导学生分析问题、解决困难,塑造学生逻辑思维能力的关键方法,根据设定有多样性、协调能力的难题,激发学生探索的主动性。数学题目的处理,一环扣一环,中间拥有紧密的联络。因而,学生学习培训要善于观察、发觉、小结知识中间的联络,把新知识与旧知识开展结合,转换难题和解决困难是深度神经网络最关键的特点,学生要依据现有经验,在类似的难题情景中举一反三,才可以能够更好地了解难题、转换难题、解决困难。在课堂教学中老师应当留意用好教材,了解、弄懂教材内容,全方位把握基本知识,理解和掌握真实的知识管理体系和能力构造。宽阔构思,一题多解。一题多解能够塑造学生答题的思索能力,更能够根据较少的题型备考较多的基本知识,并激起学生的好奇心。留意题型的变式和延伸,把握住练习题的独特点,多方面,多方位探索,塑造学生的逻辑思维能力。
结语
总而言之,数学课来自日常生活,另外数学课也服务项目于日常生活。在处理数学初中的最短路径难题时,大家必须用数学中的“转化思想”将日常生活的难题转换为“两点中间直线最短”的难题或应用中心对称的特性,根据等直线代用,将所愿线路长转换为两指定中间的距离。大家还应留意:利用中心对称处理最值问题应留意题型规定,依据中心对称的特性、利用三角形的三边关联,根据对比来表明最值问题是常见的一种方式。
参考文献
[1]王素娟 : 浅谈初中数学教学中的最短路径问题 [J], 教育实践与研究(B),2016,06:55-56.
[2]陶卫东 : 探究“最短路径”问题 [J],数学教学通讯, 2013,(25):62-64.
[3] 王晓忠 : 自制长方体魔具盒解决最短路径问题 [J], 中学生数理化(教与学),2012,(12):95.
宁阳县实验中学 山东 泰安 271400

