小学数学思想的“知”与“行”

摘要：贯穿于数学教学的整个过程始终有两根红线，一根红线是指数学知识与技能，另一根红线是指数学思想与活动经验，在数学课程标准中合称为“四基”。本文将数学思想置于数学“四基”的大背景下进行阐述。

关键词：小学;数学;“知”、“行”

小学数学中最基本的数学思想是抽象、推理、模型，还包括符号化思想、化归思想、类比思想等。数学思想的落实就像种果树一样，只有经过悉心耕耘，才能在学生心中生根、发芽、开花、结果，從而获得丰收。

一、用心深挖，让数学思想生根

要让数学思想方法真正得以落实，就得把教材中所蕴含的思想方法深入浅出地挖掘出来。教者得认真研读教材，读懂教材，全面领会编者的编写意图，找到两根红线得以发展的根——数学思想。数学思想是隐秘的，需要教师去探索和挖掘，从碎片素材中，抽丝剥茧找出数学思想的藏身之处，并当作重要目标去践行和实现。

北师大版六年级上“圆的周长”的教学，重心在于认识圆周率、学会求圆的周长。圆是一种曲线图形，学生在量圆的周长时，实际上是体会了“化曲为直”的思想。教学时，当学生想出了量圆的周长的方法后，要加以引导并小结：我们不管是“滚”、还是“绕”等，实际上都是把曲线变成线段来度量，这样的方法我们就它叫着“化曲为直”。

二、有效活动，让数学思想发芽

数学思想的落实，关键是要设计、组织、实施行之有效的教学活动。学生只有经历问题的解决过程，才能体会到数学思想的作用，理解数学思想的精髓。

北师大版四年级下册“方程的认识”，设计教学过程时，应从学生的年龄特点和认知基础出发，选取他们喜闻乐见的游戏、视频、图片、数学问题等。针对素材，设计具有引导性的问题，组织有意义的数学活动。学生在“读中理解”“疑中提问”“做中解惑”“说中交流”，逐步实现具象思维活动到抽象思维活动的转化。

学生理解到方程是为了解决生活中的实际问题而产生的，从而培养他们自觉运用方程的思想来解决生活中的实际问题。

教学中要旗帜鲜明地把数学思想作为教学的目标，通过创设问题情境，激发学生探索问题的需要。学生通过观察、实验、分析、综合、归纳、概括等过程，获得对数学思想方法的认识和感悟。

三、反复理解，让数学思想开花

数学思想的形成规律是循序渐进，螺旋上升的。学生只有经历了从教学内容中提炼、总结、理解、应用等循环往复的过程，才能从“双基”中逐步悟出数学“思想”。

1.同一数学思想，在不同学段，做到反复理解。如模型思想，在小学各阶段的数学教学中都有涉及，几乎涵盖了各册教材。模型思想不是简单的重复，而是不断发展，不断深入。各个阶段的教学，应不断挖掘与该学段相随的模型思想，让学生在教学活动中经过反复感悟，反复理解，模型思想才能逐步深刻。

2.同一数学思想，同一教学内容，做到反复理解。如乘法分配律，是运算律教学中的一个难点。我们应该给予学生更多的时间和素材，创造多种多样的学习活动，让学生反复地实践、不断地理解。只有学生对乘法分配律的“型”牢记于心时，才来小结乘法分配律。经过这样的反复理解，学生才能深刻地构建起乘法分配律的模型。

四、不断运用，让数学思想结果

数学思想的落实，最终目标是运用。经常运用数学思想，学生会在不断的运用中感受到数思想的意义，从而更乐意、更主动地去感悟数学思想，增强学习的兴趣，形成良性循环。

如“数形结合”的思想，在小学数学教学中运用十分广泛，在不同的学习阶段，运用“数形结合”的思想，可以帮助学生把数学问题具体化、形象化、简单化，提高解决问题的效率。

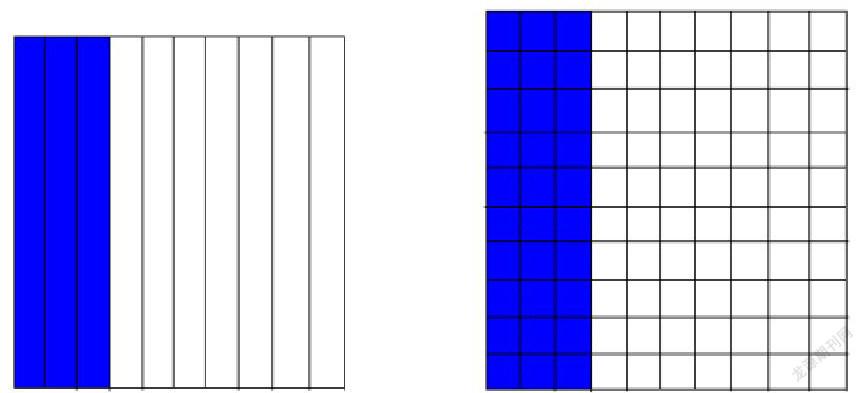
如：学生对于“小数0.3与0.30”容易产生歧义。通过图形就可以帮助学生认识“0.3与0.30”之间的差异，理解“小数0.3与0.30”的意义不同：0.3是把整数“1”平均分成10份，表 示其中的3份。0.30表示把整数“1”平均分成100份，表示其中的30份。 （如上图）。

从图中学生不仅能正确地区别清楚0.3与0.30之间意义的差异，0.3表示3个十分之一，0.30表示30个百分之一，而且能通过图形的比较，发现这两个数其实大小是一样的：0.3=0.30。

数学思想的“知”，就是要有行动的目标;数学思想的“行”，就是要有落实行动的方法。只有知行合一，不断实践，才能让数学思想之树常青。

参考文献：

1. 王永春. 《小学数学与数学思想方法》[J]. 小学教学：数学版， 2015（1）：6-6.

广东省佛山市顺德区容桂海尾小学 黄学全