从旋转的角度慧眼识图

徐奎奎

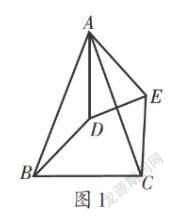
【典例重现】如图1，△ABC、△ADE均是顶角为42°的等腰三角形，BC，DE分别是底边，图1中的哪两个三角形可以通过怎样的旋转而互相得到？（八年级下册第89页第12题）

解析：若想通过旋转得到，这两个三角形必须全等，且对应点到某一定点的距离必须相等. 根据“SAS”可知△ABD ≌ △ACE，且点B和点C、点D和点E、点A和点A分别是对应点，且点A是旋转中心. 因此，将△ABD绕点A逆时针旋转42°就可以得到△ACE;同样将△ACE绕点A顺时针旋转42°就可以得到△ABD.

【启示】 用旋转的视角观察图形的结构特征，通常能够发现其中隐含着三角形全等的关系. 旋转只改变图形的位置，不改变图形的大小（全等三角形的对应角相等、对应边相等），因此可用旋转变换线段的位置，将几个分散的条件聚集在一起，为顺利求解奠定基础.

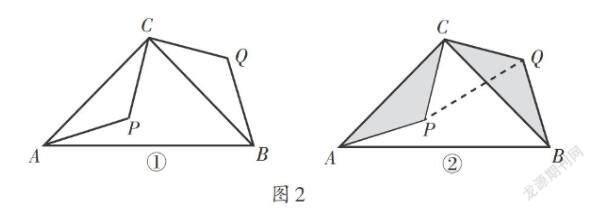
【慧眼识图1】 以等腰直角三角形为载体的基本图形，如图2.

【旋转策略】 如图2①，P为等腰直角三角形ABC内一点，∠ACB = 90°，将△ACP绕点C逆时针旋转90°，使CA与CB重合，经过这样旋转变化，把△ACP移动到△BCQ的位置（如图2②），从而解决问题.

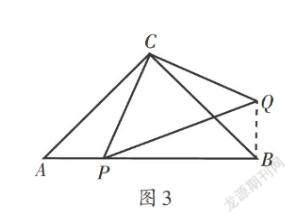
例1（2020·内蒙古·通辽）如图3，在△ABC中，∠ACB = 90°，AC = BC，点P在斜边AB上，以PC为直角边作等腰直角三角形PCQ，∠PCQ = 90°，探究PA2，PB2，PC2三者之间的数量关系.

解析：观察图3发现△BCQ是由△ACP绕点C逆时针旋转90°得到的，这样将AP转化到线段BQ的位置，把PA，PB聚集到Rt△PBQ中，于是连接BQ.

∵∠ACB = ∠PCQ = 90°，∴∠ACP = ∠BCQ，

∵AC = BC，PC = QC，∴△ACP ≌ △BCQ（SAS），

∴AP = BQ，∠CBQ = ∠A = 45°，

∵∠CBP = 45°，∴∠ABQ = ∠CBP + ∠CBQ = 90°，

∴在Rt△PBQ中，BQ2 + BP2 = PQ2，∴AP2 + BP2 = PQ2，

∵△PCQ是等腰直角三角形，

∴PQ2 = 2PC2，∴AP2 + BP2 = 2PC2.

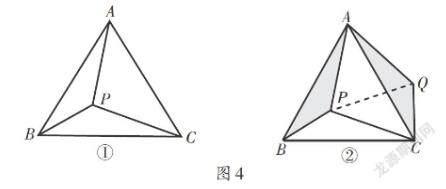
【慧眼识图2】 以等边三角形为背景的基本图形，如图4.

【旋转策略】 如图4①，P为等边三角形ABC内的一点，将△ABP绕点A逆时针旋转60°，使AB与AC重合，经过这样旋转变化，把分散的线段PA，PB，PC聚集到图4②的等边三角形APQ中.

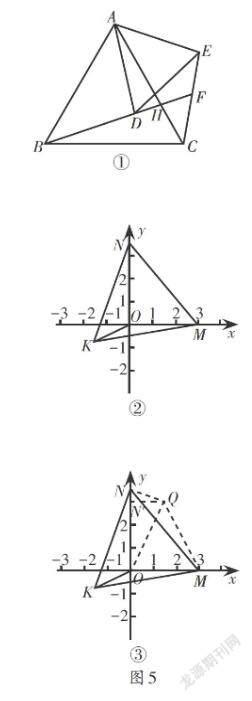
例2（2020·山东·威海）（1）如图5①，△ABC与△ADE都是等边三角形，直线BD，CE交于点F. 直线BD，AC交于点H. 求∠BFC的度数.

（2）如图5②，在平面直角坐标系中，点O的坐标为（0，0），点M的坐标为（3，0），N为y轴上一动点，连接MN. 将线段MN绕点M逆时针旋转60°得到线段MK，连接NK，OK. 求线段OK长度的最小值.

解析：（1）观察图5①发现△BAD与△CAE是一对绕点A旋转60°的全等三角形，旋转变换将∠ABD转化至∠ACE的位置，在△BFC中，利用三角形内角和定理获取问题答案.

∵△ABC与△ADE是等边三角形，

∴AB = AC，AD = AE，∠BAC = ∠DAE = 60° = ∠ABC = ∠ACB，

∴∠BAD = ∠CAE，∴△BAD ≌ △CAE（SAS），∴∠ABD = ∠ACE，

∵∠ABD + ∠FBC = ∠ABC = 60°，∴∠ACE + ∠FBC = 60°，

∴∠BFC = 180° - ∠FBC - ∠ACE - ∠ACB = 60°.

（2）將线段MN绕点M逆时针旋转60°得到线段MK，

∴MN = MK，∠NMK = 60°，∴△MNK是等边三角形，

∴MK = MN = NK，∠NMK = ∠NKM = ∠KNM = 60°，

由题意可知点K的位置随着点N的变化而变化，受旋转模型启发，可将△MOK绕点M顺时针旋转60°得到△MQN，连接OQ（如图5③），可得NQ = OK，只需求QN的最小值，显然当QN⊥y轴时，NQ有最小值.

由旋转可知△MOK ≌ △MQN，∠OMQ = 60°，

∴OK = NQ，MO = MQ，

∴△MOQ是等边三角形，∴∠QOM = 60°，∴∠NOQ = 30°，

∵OK = NQ，∴当NQ为最小值时，OK有最小值.

由垂线段最短可得：当QN'⊥y轴时，N'Q有最小值，

此时，QN'⊥y轴，垂足为N'，∠N'OQ = 30°，

∴N'Q [=12]OQ [=32]，∴线段OK的最小值为[32].