带肋预应力混凝土复合墙板的抗弯性能

梁远森 王宁 季可凡 侯和涛

摘 要：将传统复合墙板平板层改为带肋层，优化截面的混凝土配置，从而降低复合墙板自重，在墙板两侧对称施加预应力筋，增强复合墙板的抗裂性能。为研究带肋预应力混凝土复合墙板的抗弯性能，进行了3个试件在均布力作用下的抗弯试验，分析该混凝土复合墙板的力学性能和变形模态。通过理论分析推导该混凝土复合墙板的抗弯承载力计算公式，采用ABAQUS软件进行该混凝土复合墙板的对比模拟，并对肋板角度参数进行模拟分析。结果表明：带肋预应力混凝土复合墙板与平板混凝土复合墙板存在近似的弯曲响应;带肋预应力混凝土复合墙板的抗弯承载力与平板混凝土复合墙板相比有所下降，但降幅小于自重降幅;预应力的施加显著提高了混凝土复合墙板的承载力和抗裂性能;提出的混凝土复合墙板的承载力计算公式、有限元模型均与试验结果吻合较好。

关键词：复合墙板;混凝土墙板;带肋墙板;预应力;抗弯试验;抗弯性能

Abstract： The ribbed prestressed concrete composite wall panel changes the traditional composite wall panel layer into the ribbed layer， and optimizes the concrete configuration of the section to reduce the self-weight of the composite wall panel. Prestressed reinforcement is added to both sides of the wall panel， which can increase the crack resistance of composite wall panel. In order to study the bending performance of the concrete composite wall panels， the bending test of three specimens under uniform load was carried out， and the mechanical properties and deformation modes of the concrete composite wall panel were analyzed. The calculation formula of flexural bearing capacity was derived through theoretical analysis.The comparative simulation and ribbed plate angle parameter analysis of the composite wall panels were conducted by the finite element software ABAQUS. The results showed that the ribbed prestressed composite wall panel had similar bending behavior to the traditional composite wall panel. The flexural capacity of the ribbed prestressed composite wall panels decreased， but its reduction was less than the self-weight reduction. The application of prestressing could significantly improve the bearing capacity and crack resistance of the composite wall panel. The proposed calculation formula of the bearing capacity and the finite element simulation results of the ribbed prestressed composite wall panels were in good agreement with the experimental results.

Keywords： composite wall slabs; concrete wall slabs; ribbed wall slabs;prestress; flexural experiment;flexural performance

复合墙板作为外围护体系的一种，具有轻质节能、经济性好的显著优点，主要应用于装配式建筑中，与钢结构住宅主体相配合[1-3]。复合墙板的选用影响着装配式建筑整体力学性能的发挥以及连接节点的处理，轻质复合墙板是学者们研究的热点[2，4-5]，但目前研究内容主要集中在选用轻质材料作为复合墙板的面层来降低自重[4，6-10]，在截面形式优化方面研究很少。

传统复合墙板为三明治式平板复合结构，由中間的保温芯层和两侧的结构面层组成，其中，抗剪连接件将两侧的混凝土结构面层和保温芯层锚固为整体，共同参与工作，保证了混凝土复合墙板形成有效的组合作用[11]。然而，传统平板复合墙板的截面形式存在不合理性。分析发现，复合墙板中直接参与锚固作用的混凝土区域只占混凝土结构面层的一部分，其他位置的混凝土对锚固作用的贡献有限，如图1所示。

将传统的平板混凝土复合墙板进行截面优化，剔除部分截面的混凝土，将平板混凝土层改为带肋混凝土层，从而达到降低自重的目的。为了更好地提高带肋复合墙板的力学性能，在带肋复合墙板两侧的混凝土层内对称布置预应力筋，形成带肋预应力混凝土复合墙板，如图2所示。

为研究减重后带肋预应力混凝土复合墙板的抗弯性能，进行了均布荷载作用下不同参数的混凝土复合墙板试件的抗弯性能试验研究、理论分析和有限元模拟分析。

1 试验概况

1.1 试件设计

共设计制作了3个试件，试件尺寸如表1所示，其中，试件A为传统平板混凝土复合墙板，试件B为不加预应力的带肋混凝土复合墙板，试件C为带肋预应力混凝土复合墙板。所有复合墙板均为两侧钢筋混凝土层和中间的EPS保温层组成，采用直径4 mm的连续斜向钢丝作为抗剪连接件，沿复合墙板长度方向的两端设置长100 mm的实心混凝土区。两侧的混凝土层内均配置Ф3@50的双向钢丝网片，钢丝网片由4列连续斜向钢丝焊接连接，斜向钢丝的倾斜角度为45°，相邻两列斜钢丝间距为150 mm，试件构造如图3所示。

如图4所示，带肋混凝土复合墙板两侧对称布置等腰梯形混凝土肋板，试验后期，实测得出采用带肋混凝土板的试件B与采用平板混凝土板的试件A相比，重量减少20.8%。试件C与试件B均为带肋混凝土复合墙板，不同的是，试件C增设两侧对称的预应力筋。预应力的施加方式为先张法，控制应力为0.75倍的预应力筋抗拉强度标准值。

1.2 试验加载装置及测点布置

采用相同质量的沙袋均匀布置于复合墙板上，以实现对均布力的模拟，沙袋重量均为7.5 kg，实际加载装置如图5所示。试验的支承结构为三角形鋼架，混凝土复合墙板两端的搁置长度均为75 mm。

图6为各混凝土复合墙板的位移计布置图，3个试件的位移计位置均相同，依次编号为L1～L5。图7（a）为复合墙板的混凝土应变测点布置图，各复合墙板试件均设8处应变片，保证上、下表面位置对称，其中，复合墙板上表面设置应变片A1～A4，下表面对应设置应变片B1～B4，目的是方便后期分析复合墙板上、下结构层的协调工作程度。图7（b）为混凝土复合墙板的纵筋应变测点布置图，各复合墙板试件的纵筋处设12个应变片，保证受拉、受压处位置对称，其中，复合墙板受压处纵筋设置应变片E1～E6，受拉处纵筋对应设置应变片F1～F6。

1.3 材性试验结果

混凝土和钢丝的材性按照材性试验规程[12-13]进行测试，混凝土为C40自密实混凝土，28 d龄期混凝土立方体抗压强度均值为41.4 MPa，弹性模量为30.8 GPa。钢材材性见表2。

2 试验结果及分析

2.1 试验现象

3个混凝土复合墙板试件试验现象相似：初始加载阶段，复合墙板跨中处的挠度增加缓慢，直至加载到开裂荷载，开始出现肉眼可见的微小裂缝;持续加载，复合墙板挠度增速加快，裂缝数量明显增加，已有裂缝逐渐增大;当接近极限状态时，试件跨中位移激增，弯曲变形明显，裂缝区域明显变大;直至复合墙板底部的纵筋断裂，试验结束，破坏现象见图8（a）。对于试件C，其裂缝宽度达到1.5 mm时停止加载，定义此时为试件C的破坏状态，见图8（b）。

试验结束后，对带肋混凝土复合墙板进行剖面观察，如图8（c）所示，发现混凝土肋板形状清晰可见，混凝土均匀密实，表明试件制作质量达到预期。

所有复合墙板试件的裂缝分布均为较明显的正截面受弯垂直裂缝，均呈现多而密的特点，开展较为充分，如图9所示。这是因为墙板下层设有钢丝网。

各试件的荷载统计情况（包括自重）如表3所示。带肋混凝土层的试件B与平板混凝土层的试件A相比，自重减少20.8%，但承载力仅减少10%左右。与试件A、试件B相比，试件C的开裂荷载以及极限荷载均有大幅增加，表明预应力筋对混凝土复合墙板的抗弯承载力有积极影响。3种复合墙板中，带肋预应力混凝土复合墙板抗弯性能最为优越。

所有混凝土复合墙板试件的开裂荷载和极限荷载比值均在40%～51%范围内，说明复合墙板在开裂后仍有充分的承载力安全储备。

2.2 荷载位移试验结果分析

从图10可以看出，试件B与试件A的荷载位移曲线相近，试件B的抗弯极限承载力较试件A有所降低;试件C的曲线斜率明显大于其他两个试件，抗弯承载力大大提升，位移变形得到有效控制。以上结果表明：带肋混凝土复合墙板与传统平板混凝土复合墙板相比，承载力虽有一定程度降低，但整体抗弯性能相近;带肋预应力混凝土复合墙板的抗弯性能明显优于另两种复合墙板，预应力的施加能够显著提升混凝土复合墙板的抗弯刚度和承载力，有利于限制混凝土复合墙板的位移。

2.3 混凝土应变分析

由图11得出，在复合墙板试件未开裂过程中，各试件混凝土应变逐渐递增，趋势大致呈线性，各试件A1和B1处的代数值之和大致为0，说明复合墙板两侧混凝土层的应变能够较好地保持一致，试件整体具有良好的组合作用，在理论推导时可以将其作为一个整体进行研究。

2.4 纵筋应变分析

图12为各个试件跨中受拉、受压纵筋的应变图。比较各试件加载初期的纵筋应变可以看出，在荷载相同的情况下，同一侧的纵筋应变具有一定差异，表明无论在受拉区还是受压区，纵筋的应力值均呈不均匀分布，导致部分复合墙板区域出现提前开裂的情况，因此，在理论计算混凝土复合墙板的抗弯承载力时，需对其加以考虑。

3 承载力的理论计算

3.1 复合墙板组合程度的确定

根据两侧混凝土结构层的协同工作程度，复合墙板的组合程度主要分为完全组合、部分组合和完全不组合[6]。不同组合作用性质的混凝土复合墙板具有不同的受力性能，故理论计算时应先确定混凝土墙板的组合程度。

借鉴聂建国等[14]提出的组合梁判定方法，若混凝土复合墙板的斜钢筋传递的剪力值超过下侧混凝土板中纵向受拉钢丝的承载力总和，则定义该混凝土复合墙板属于完全组合。因此，定义μ为复合墙板组合程度系数，表达式为

若μ>1，则该试件属于完全组合。理论分析各复合墙板试件的组合程度系数见表4，由表4可知，所有试件的μ均大于1，说明各试件均达到完全组合。

3.2 复合墙板开裂弯矩的理论计算

带肋预应力混凝土复合墙板的预应力筋为墙板上、下两侧对称布置，同侧预应力筋会分别对两侧混凝土层施加预压力、预拉力。下侧预应力筋对复合墙板下混凝土层施加有效预压力σ单侧压，对复合墙板上混凝土层施加有效预拉力σ单侧拉。

式中：Np0为混凝土复合墙板的单侧预应力筋有效总应力;ep0为混凝土复合墙板的单侧预应力筋作用點偏心距;A0为换算截面面积;I0为换算截面惯性矩;y0为受拉边缘到中性轴距离。

复合墙板试件两侧混凝土层之间的剪力靠斜钢筋传递，所以，剪力传递主要存在于靠近于斜钢筋的混凝土部分，而不是复合墙板的整个混凝土层，这将引起应力不均匀分布。同样，带肋复合墙板试件的梯形肋板也能够引起应力的不均匀分布，因此，“剪力滞效应”是混凝土复合墙板受力分析时不可忽视的因素。

式中：ftk为混凝土的轴心抗拉强度标准值。将Mcr理论和Mcr试验代入式（6），求得各个误差eMcr，从图13可看出，λ最优值=0.52，此时开裂荷载误差处于最小值。

表5为复合墙板各试件的试验开裂弯矩Mcr试验和理论计算开裂弯矩Mcr理论的对比分析。当系数λ=0.52（考虑剪力滞效应）时，3个复合墙板Mcr试验与Mcr理论的最大误差为18.01%;当系数λ=1（未考虑剪力滞效应）时，3个复合墙板Mcr试验与Mcr理论二者的误差均大于50%，远超过系数λ=0.52时的误差，所以，在分析混凝土复合墙板开裂弯矩时应合理考虑剪力滞效应。

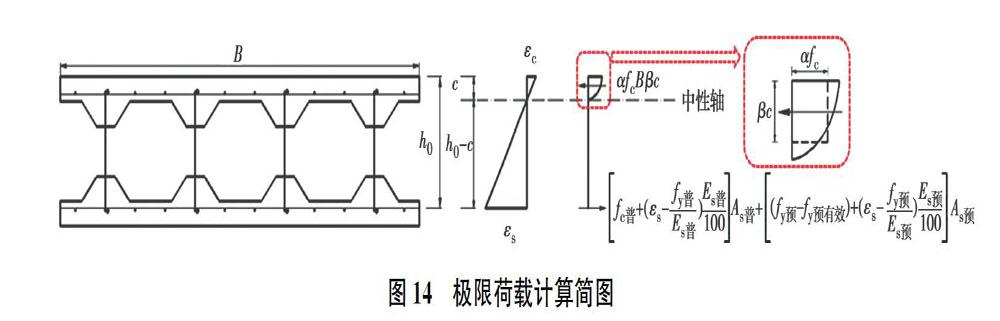
式中：fy、As分别为钢筋的抗拉强度、截面面积;fc为混凝土的轴心抗压强度;α为受压区混凝土等效矩形应力图的应力值与fc的比值;β为等效矩形应力图的换算受压区高度与截面实际受压区高度的比值;c为混凝土的受压区高度;B为受弯构件的截面宽度。

复合墙板上侧混凝土结构层应变根据材料性质得出，纵筋应变可根据式（11）转换为混凝土应变。考虑到预应力筋发挥有效预拉力的过程必然伴随着应变的产生，受拉纵筋（包含预应力筋）达到屈服强度后，弹性模量Es也会有一定程度降低。复合墙板的钢筋选用双线性模型，假定钢筋屈服后Es降低为原来的0.01，得出带肋预应力混凝土复合墙板的极限承载力为

式中：fy预有效为混凝土复合墙板的预应力筋有效预拉力;Es普为混凝土复合墙板的弹性阶段普通钢筋弹性模量;Es预为混凝土复合墙板的弹性阶段预应力筋弹性模量。

4 有限元分析

4.1 复合墙板模型概况

应用ABAQUS软件进行混凝土复合墙板抗弯性能的模拟，进一步与所做的试验、理论计算相对比分析。模拟复合墙板的混凝土本构关系为塑性损伤模型，建模应用实体单元C3D8R;模拟复合墙板的钢筋本构关系为理想弹塑性模型，建模应用梁单元B31。带肋复合墙板模型如图16所示。

为了模拟试验加载状态，复合墙板有限元模型的边界条件选取与试验保持一致，模拟建立两块钢垫板模型置于复合墙板试件的底部，位置与试验时的三角形钢架保持一致。试验中的加载方式采用沙袋均布方法，因此，在模拟过程中采用pressure命令对模型施加外荷载。

4.2 应力模拟分析

以试件B的应力模拟为例，从图17得出，复合墙板的混凝土应力分布呈明显的波浪形，处在波峰位置（靠近斜钢筋处）的混凝土部分应力约为3 MPa，而处在波谷位置（远离斜钢筋处）的混凝土应力约为1 MPa，二者差距明显，这也验证了理论分析采用混凝土应力不均匀分布假定的正确性。

图18显示出复合墙板中接触斜钢筋的纵向钢筋区域应力值约为550 MPa，但不与斜钢筋直接接触的纵向钢筋区域应力值约为220 MPa，二者差距明显，与理论分析采用钢筋应力不均匀分布的假定相同。

4.3 荷载位移曲线分析

图19为各试件跨中荷载位移曲线的有限元模拟与试验对比。各试件模型的跨中荷载位移曲线与试验走势基本相同，均为二折线模型状态。对比曲线在弹性阶段吻合较好，在弹塑性阶段存在一定的差距，这是由于复合墙板模型在有限元分析时并未考虑部件存在的初始缺陷和加载过程中试件材料的损耗破坏，使得各个复合墙板模型的刚度在一定程度上较试验值有所增大。各试件模拟得到的跨中荷载位移曲线与试验总体吻合度较高，故建立的混凝土复合墙板有限元模型较为可靠，可以实现对复合墙板试件的快速分析，为后续影响参数的研究提供了便利。

4.4 肋板形状参数分析

试验中混凝土肋板的形状均为底角为45°的等腰梯形肋板，并未对其他肋板形状进行研究，因此，采用有限元模拟的方法分析不同底角角度的等腰梯形肋板以及圆形肋板对带肋混凝土复合墙板抗弯承载力的影响。圆形肋板截面及不同底角的等腰梯形肋板截面如图20所示，底角θ分别为30°、45°、60°、75°以及90°。

图21为不同肋板形状的带肋混凝土复合墙板跨中荷载位移曲线。从图21可以发现，所有混凝土复合墙板中，采用圆形肋板的试件在受力过程中抗弯刚度呈较显著的降低趋势。经计算得出，圆形肋板混凝土复合墙板的减重比为36.9%，90°角肋板混凝土复合墙板的减重比为40%，但圆形肋板混凝土复合墙板模型的跨中位移显著增加，表明圆形肋板混凝土复合墙板的刚度退化较明显，在实际工程应用中该类型复合墙板性价比不高。

当角度θ在30°～90°之间变化时，各模型在弹性阶段的跨中挠度大小相近，表明肋板角度的变化不会明显影响带肋混凝土复合墙板的弯曲行为;各模型的开裂荷载具有一定的差异性，从30°角肋板到90°角肋板复合墙板的开裂荷载逐渐减小。

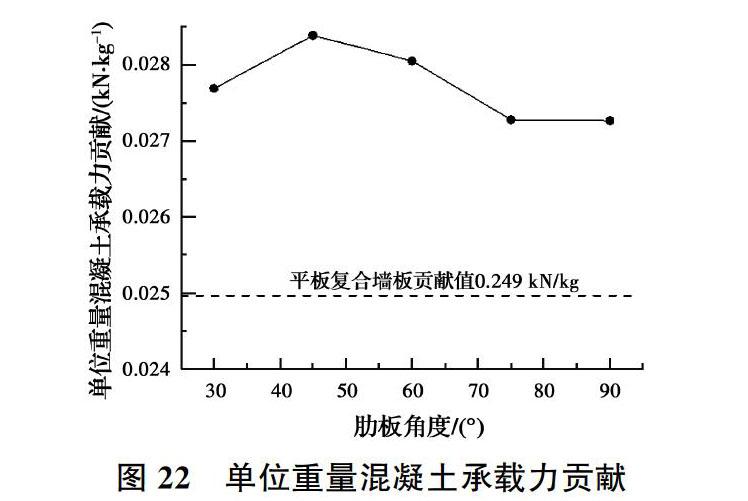
图22为不同肋板角度模型单位重量混凝土对墙板开裂承载力的贡献值。不同肋板角度的试件单位重量混凝土承载力贡献值明显超过传统平板复合墙板;45度角等腰梯形肋板的试件模型达到贡献值的峰值点，贡献值最大，故45°等腰梯形肋板为肋板角度的最佳选择。

5 结论

1）带肋预应力混凝土复合墙板与传统平板复合墙板的弯曲响应差异不明显，但预应力的施加能够显著提升混凝土复合墙板的力学性能。

2）与传统混凝土复合墙板相较，带肋混凝土复合墙板的抗弯性能虽有一定程度下降，但与其质量降幅相比，带肋混凝土复合墙板抗弯承载力降幅明显小于质量降幅。带肋预应力混凝土复合墙板有着极为优异的抗弯能力和抗裂能力，其开裂荷載较传统墙板提升1倍左右，达到9.18 kN/m2，可用于对承载能力有更高需求的高空环境。

3）建立的混凝土复合墙板承载力理论计算公式、有限元模型均与试验结果吻合较好，可以为后续相关研究提供一定参考。

4）肋板角度对带肋混凝土复合墙板的开裂荷载有一定的影响，45°等腰梯形肋板为肋板角度的最佳选择。

参考文献：

[1] 包芸芸. 钢框架外挂轻质复合墙板结构抗震性能研究[D]. 北京： 北京建筑大学， 2020.

BAO Y Y. Research on seismic performance of steel frame structure with light composite wall [D]. Beijing： Beijing University of Civil Engineering and Architecture， 2020. （in Chinese）

[2] 侯和涛， 王文豪， 曹运昌， 等. 与足尺钢框架柔性连接的外挂复合墙板振动台试验研究[J]. 建筑结构学报， 2019， 40（12）： 21-31.

HOU H T， WANG W H， CAO Y C， et al. Shake table tests of exterior sandwich composite walls flexibly connected to full-scale steel braced frames [J]. Journal of Building Structures， 2019， 40（12）： 21-31. （in Chinese）

[3] 吴香国， 陶晓坤， 于士彦， 等. 高性能复合夹芯外挂墙板应用研究进展[J]. 建筑结构， 2020， 50（Sup1）： 611-616.

WU X G， TAO X K， YU S Y， et al. Research progress of high-performance composite sandwich panel [J]. Building Structure， 2020， 50（Sup1）： 611-616. （in Chinese）

[4] AMRAN Y H M， RASHID R S M， HEJAZI F， et al. Response of precast foamed concrete sandwich panels to flexural loading [J]. Journal of Building Engineering， 2016， 7： 143-158.

[5] 卞文军， 范力， 李升旗. 不同连接方式预制复合墙板填充墙对框架抗震性能的影响[J]. 建筑结构学报， 2020， 41（Sup1）： 196-203.

BIAN W J， FAN L， LI S Q. Influence of prefabricated composite infilled wallboard with different connection modes on seismic behavior of frame structure [J]. Journal of Building Structures， 2020， 41（Sup1）： 196-203. （in Chinese）

[6] 陈璐. 竹筋陶粒混凝土粘结性能及复合墙板抗弯性能的试验研究与理论分析[D]. 济南： 山东大学， 2012.

CHEN L. Experimental investigation and theoretical analysis of bond properties and bending performance on composite panels of ceramic bamboo-reinforced concrete [D]. Jinan： Shandong University， 2012. （in Chinese）

[7] 张微敬， 孙雪莹， 李爱影. 轻质纤维增强复合木剪力墙拟静力试验研究[J]. 建筑结构， 2020， 50（16）： 94-99.

ZHANG W J， SUN X Y， LI A Y. Study on quasi-static test of lightweight composite wood shear walls with glass fiber-enhanced cladding [J]. Building Structure， 2020， 50（16）： 94-99. （in Chinese）

[8] 麻建锁， 李雪娜， 蔡焕琴. 预制芯柱式普通泡沫混凝土复合外墙板技术研究[J]. 混凝土， 2019（8）： 125-127.

MA J S， LI X N， CAI H Q. Research on the technology of the prefabricated core type ordinary-foam concrete composite outer wall panel [J]. Concrete， 2019（8）： 125-127. （in Chinese）

[9] 刘泰玉. FCP复合墙板抗弯性能研究[D]. 沈阳： 沈阳建筑大学， 2015.

LIU T Y. Study on the flexural performances of fiber cement composite panels [D]. Shenyang： Shenyang Jianzhu University， 2015. （in Chinese）

[10] RAJ S， RAMESH KUMAR V， BHARATH KUMAR B H， et al. Flexural studies on Basalt Fiber Reinforced Composite sandwich panel with profile sheet as core [J]. Construction and Building Materials， 2015， 82： 391-400.

[11] MOHAMAD N， HASSAN N. The structural performance of precast lightweight foam concrete sandwich panel with single and double shear truss connectors subjected to axial load [J]. Advanced Materials Research， 2013， 634-638： 2746-2751.

[12] 金属材料 室温拉伸试验方法： GB/T 228—2002 [S]. 北京： 中国标准出版社， 2002.

Metallic materials： Tensile testing at ambient temperature： GB/T 228-2002 [S]. Beijing： Standards Press of China， 2002. （in Chinese）

[13] 普通混凝土力学性能试验方法标准： GB/T 50081—2002 [S]. 北京： 中国建筑工业出版社， 2003.

Standard for test method of mechanical properties on ordinary concrete： GB/T 50081-2002 [S]. Beijing： China Architecture & Building Press， 2003. （in Chinese）

[14] 聂建国. 钢混凝土组合结构[M]. 北京： 中国建筑工业出版社， 2005.

NIE J G. Steel-concrete composite beam structure [M]. Beijing： China Architecture & Building Press， 2005. （in Chinese）

[15] 田春雨， 聂建国. 简支组合梁混凝土翼缘剪力滞后效应分析[J]. 清华大学学报（自然科学版）， 2005， 45（9）： 1166-1169.

TIAN C Y， NIE J G. Shear lag analysis of simply supported composite steel-concrete beams [J]. Journal of Tsinghua University （Science and Technology）， 2005， 45（9）： 1166-1169. （in Chinese）

[16] 混凝土結构设计规范： GB 50010—2010 [S]. 北京： 中国建筑工业出版社， 2011.

Code for design of concrete structures： GB 50010-2010 [S]. Beijing： China Architecture & Building Press， 2011. （in Chinese）

（编辑 王秀玲）