基于随机权重粒子群算法的SCARA机器人动力学参数辨识
王保民,齐湛江,闫瑞翔,刘洪芹
(兰州理工大学机电工程学院,730050,兰州)
SCARA机器人是一种有4个自由度的平面关节型机器人,它能模仿人类手臂的动作,可完成零件安装和物品搬运等工作,已广泛应用于塑料、汽车、电子、药品和食品等工业领域[1]。为适应机器人高速度、高精度与智能化发展的需要,建立精确的SCARA机器人动力学模型,对提高其控制精度与运动精度具有重要意义[2-3]。然而,机器人是一个多变量、强耦合的非线性系统,为了准确建立机器人动力学模型,通常需要对其动力学参数进行辨识[4-5]。
最小二乘法是传统的参数辨识方法,张铁等运用牛顿欧拉法建立SCARA机器人动力学模型,采用最小二乘法辨识出较高精度的机器人动力学参数[6]。最小二乘法辨识精度高,但在计算量较大时无法满足实时性要求[7]。丁力等基于加权最小二乘法与人工蜂群算法相结合的辨识算法对工业机器人动力学参数进行了辨识,并通过实验验证了该算法在力矩辨识中的精度[8]。孙玉阳等利用遗传算法对工业机器人动力学模型进行了参数辨识,该算法可以有效地避免局部最优解[9]。刘宇等采用小区间生成法和大变异策略对遗传算法进行了改进,有效提高了空间机器人动力学参数的辨识精度[10]。传统粒子群算法也常用于机械臂各关节动力学参数的辨识,但该算法存在搜索空间有限,易陷入局部最优解的问题[11-12]。王跃灵等利用改进粒子群遗传算法对柔性关节机器人动力学进行参数辨识,该算法采用动态自适应调整策略,有效提高了粒子群算法收敛速度[13]。王金磊为了得到上肢康复机器人前两关节的动力学参数,在小范围、局部空间内通过变参数粒子群算法得到精确的参数[14]。
上述研究通过不同的算法有效地提高了机器人动力学参数的辨识精度和效率,但在大计算量下,仍存在搜索空间有限、极易陷入局部最优解等问题。针对此问题,本文以台达公司的DRS40L3型SCARA机器人为研究对象,将机器人第3、4关节与未知小负载固联在第2关节上进行结构简化,基于Lagrange法建立带负载的机器人动力学数学模型,确定需要辨识的末端动力学参数。在传统粒子群算法(TPSO)的基础上,提出一种随机权重粒子群算法(RWPSO)对机器人动力学参数进行参数辨识,并通过仿真实验验证该方法的有效性。
1 SCARA机器人动力学数学模型
SCARA机器人结构如图1所示,它有3个轴线相互平行的旋转关节,在平面内进行定位和定向,另一关节是用于完成垂直平面工作的移动关节。
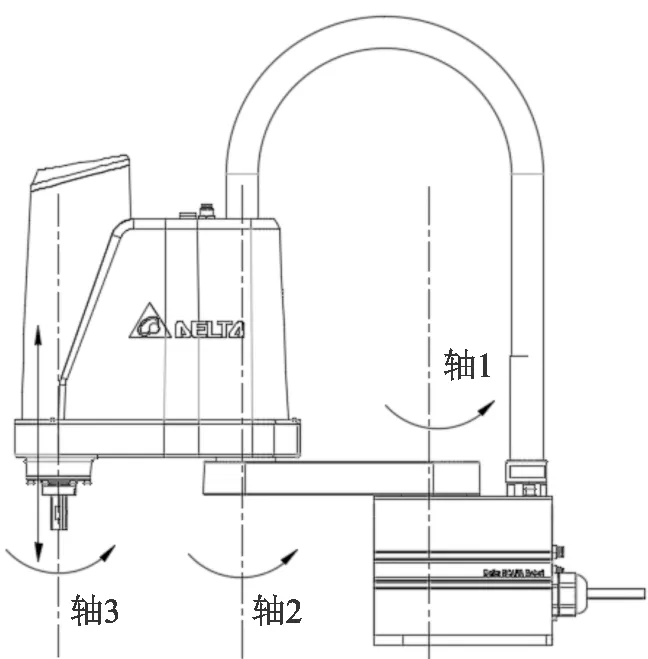
图1 SCARA机器人结构图Fig.1 SCARA robot structure diagram
SCARA机器人3、4关节质量加起来远远小于1、2关节的质量,为了简化动力学计算,提高参数辨识的精度和效率,将SCARA机器人的第3、4关节与未知小负载统一成整体负载体,变成小臂的一部分[15-16]。简化后SCARA机器人结构如图2所示。
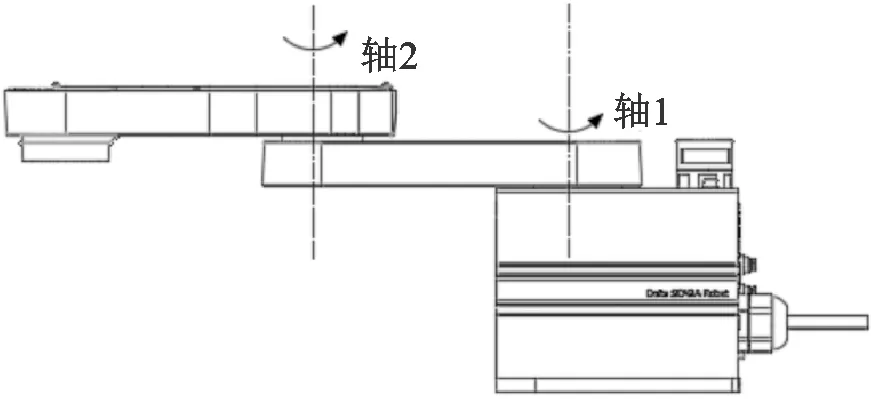
图2 SCARA机器人结构简化图Fig.2 Simplified diagram of SCARA robot structure
对于n自由度关节串联机器人,忽略摩擦的动力学模型为
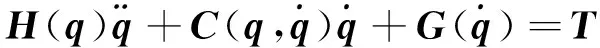
(1)
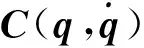
带有未知小负载两关节机械臂结构如图3所示。SCARA机器人运行中的摩擦力矩较小,并且摩擦力矩很难精确建模[17]。因此,为降低辨识成本和提高辨识精度,在不改变模型的前提下,把其他因素的影响通过辨识过程包含进机械臂的惯性参数中,得到一组满足计算精确性的综合参数。如图3所示,二连杆机器人由7个惯性参数组成,包括:
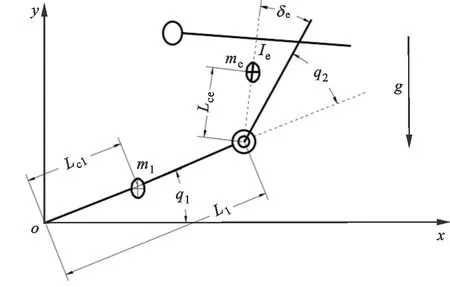
图3 带负载的两关节机械臂结构图Fig.3 Structure diagram of two-joint manipulator with load
(1)质量m1、me;
(2)质量中心到第1、2关节的距离Lc1、Lce;
(3)惯性参数I1和Ie分别为
(4)质量中心到第2机械臂的夹角δe。
由于第2个关节和负载被视为一个整体,导致参数发生了变化[18-19],因此有4个未知物理参数需要辨识,分别是me、Ie、Lce、δe。
基于Lagrange法的二关节机器人的动力学方程为
(2)
(3)
(4)
式中:m1为关节1的质量;I1为相对杆件质心的转动惯量;L1为机械臂连杆长度;q1、q2为关节角;g为重力加速度。
整合式(3)中的各种参数,将式(3)改写为ax=b的线性形式
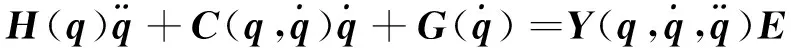
(5)
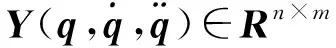
(6)
(7)
E矩阵的各个参数向量为
(8)
通过上述线性化与参数重组将复杂的非线性辨识问题转化为线性模型辨识问题,得到的惯性参数集有助于减少机器人动力学计算量与提高参数辨识的鲁棒性。
2 改进粒子群优化算法参数辨识
2.1 基本粒子群算法
粒子群算法(PSO)是一种参数计算的优化方法,其中每个优化问题的解都是搜索空间中的一只鸟,称为粒子,所有粒子都有一个由被优化函数决定的适应值。每个粒子拥有一个速度来决定它们飞行的距离与方向,且追随当前的最优粒子在解空间中搜索。
粒子速度及更新位置公式为
(9)
(10)
2.2 基于随机权重的粒子群算法
PSO中,参数粒子向自身历史最佳位置和群体历史最佳位置聚集,会形成粒子种群的快速趋同效应,容易陷入局部极值、早熟收敛或者停滞现象,导致参数辨识的不精确[20]。尤其是惯性权重影响参数微粒的局部与全局最优搜索能力,较大的权重有利于跳出局部最优,而较小的权重会增强局部搜索能力,有利于算法收敛[21-22]。针对PSO容易在搜索空间有限、极易陷入局部最优解、收敛速度慢的问题,本文提出采取随机选取权重值的方法,使得参数粒子的历史速度对当前速度的影响是随机的,可有效增大搜索范围,防止参数陷入局部最优解,加快参数辨识速度,提高参数辨识精度。
在随机权重法中,需要辨识的动力学参数在随机权重的影响下能快速跳出局部较小的搜索范围,在大搜索范围内加快辨识速度,得到精确的最优参数。随机权重w的计算公式如下
(11)
式中:μ是参数调整因子;N(0,1)表示标准正态分布的随机数;rand(0,1)表示0到1之间的随机数。随机权重PSO能在一定程度上避免陷入局部最优,增大参数粒子搜索的范围,有助于提高机械手末端参数辨识的精确性。SCARA机器人动力学参数辨识的流程如图4所示。
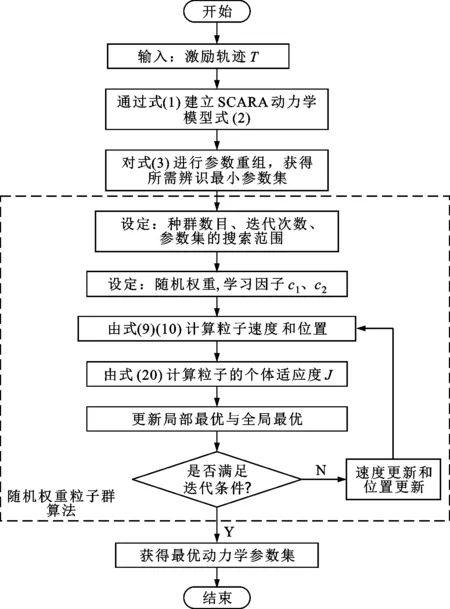
图4 随机权重粒子群算法参数辨识流程图 Fig.4 Flow chart of parameter identification of PSO algorithm with random weight
2.3 随机权重粒子群算法的稳定性和收敛性分析
假设群体粒子数为ψ,则群体粒子的全局最好位置为
(12)
令θ1=c1r1,θ2=c2r2,θ=θ1+θ2,则式(9)(10)可整理为
(13)
w、θ1、θ2在迭代过程中自适应变化,即θ=c1r1+c2r2随着迭代在(0,c1+c2)区间随机变化。此时,C(t)属于时变矩阵,根据系统理论,可得
(14)
其中Φ(t,k)为系统状态转移矩阵,即
Φ(t+1,k)=C(t)Φ(t,k)
(15)
而Φ(t,0)=C(t-1)C(t-1)…C(0)。
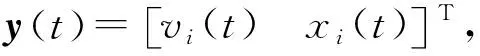
(1)V(y(t))≥0;
(2)ΔV(y(t))=V(y(t+1))-V(y(t))≤(‖C(t)‖-1)‖y(t)‖,而w、θ1、θ2的取值又使得‖C(t)‖<1,所以ΔV(y(t))负定;
(3)‖y(t)‖→∞时,有V(y(t))→∞。
根据李雅普诺夫稳定性定理,该系统是渐进稳定的,即算法具有稳定性。
由式(14)可得,在C(t)的特征值的模均小于1时,有
(16)
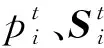
3 实验结果与分析
3.1 结构简化结果仿真验证
本实验选用台达4自由度DRS40L3型SCARA机器人,其基本参数见表1。

表1 SCARA机器人基本参数
为了验证机器人模型简化的可行性,用ADAMS软件建立机器人几何模型,并设定机器人关节激励轨迹,通过动力学仿真实验比较简化前后关节1、2力矩的大小,验证SCARA机器人模型简化成二自由度的可行性。机器人简化前为正常状态下机器人运动,输出第1、2关节的力矩;机器人简化后将第3、4关节看作负载添加在机器人小臂上,输出第1、2关节的力矩。具体仿真实验分为2部分。
(1)设定激励轨迹。考虑到DRS40L3型SCARA机器人技术性能指标以及4个关节的运动特性与约束,关节1、2输入相同的轨迹为
qd=1-cos(0.4πt)
(17)
则速度与加速度分别为
(18)
(2)施加负载。根据机器人的负载范围,在SCARA机器人末端施加0.4、0.8和1.2 kg的负载,则简化后机器人负载为施加负载加上第3和4关节总质量(0.244 kg)。通过机器人D-H参数可以将末端整体负载力矩转化到关节2上,通过观察关节1、2的输出力矩变化,确定SCARA机器人末端负载能力的大小。
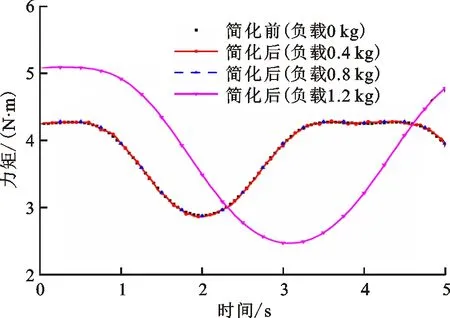
(a)关节1力矩
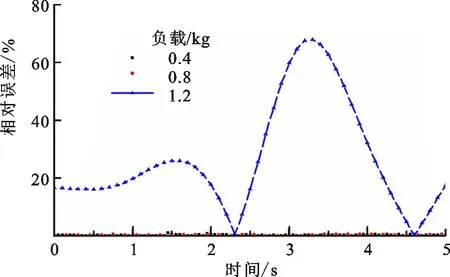
(b)关节1误差
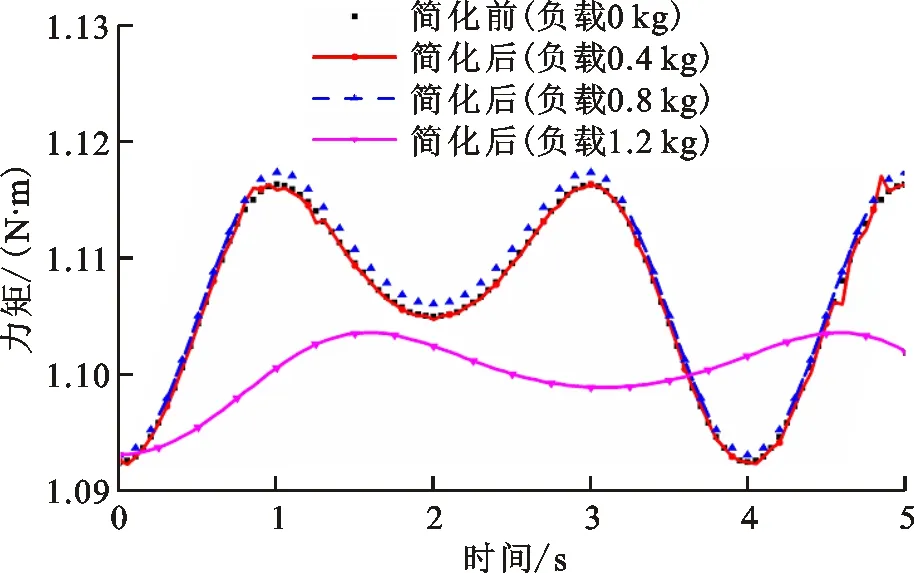
(c)关节2力矩

(d)关节2误差图5 机器人模型简化前后关节1、2的输出力矩Fig.5 Output torque of joints 1 and 2 before and after robot model simplification
仿真运行时间t=5 s,关节1和2的力矩输出如图5所示。从图中可以看出,施加负载分别为0.4、0.8和1.2 kg时,结构简化前后关节1的力矩最大相对误差分别为0.32%、0.46%和70%,关节2的力矩最大相对误差分别为0.16%、0.5%和1.5%。由此可以得出,机器人末端负载质量在0~0.8 kg时,结构简化前后关节1、2的输出力矩变化很小,相对误差在可控范围内。该仿真结果与文献[16,18]的研究结果基本一致,均表明一定的载荷范围内SCARA机器人简化为二自由度是可行的。
3.2 仿真辨识实验及结果分析
根据前面分析,选择在负载0.4 kg下进行辨识仿真实验。在辨识仿真实验中,利用MATLAB建立SCARA机器人动力学模型,给关节1、2输入激励信号,获取机器人不同姿态下的位置、速度以及相对应的各关节力矩。实验设计的输入激励曲线为
(19)
分别采用基本PSO与随机权重PSO对系统进行辨识。选取种群数为200,学习因子c1为1.3、c2为2,惯性权重为1.2,最大迭代次数为200。定义适应度函数为
(20)
辨识过程中适应度变化曲线如图6所示。由图可知,应用随机权重PSO得到的初始粒子搜索范围(0~730)明显大于基本PSO的搜索范围(0~371)。在更新位置与速度信息时,基本PSO经历大约50代达到收敛,而改进后PSO经历大约26代达到收敛,由此说明改进后的算法在收敛速度与参数粒子搜索范围上均得到明显提高。
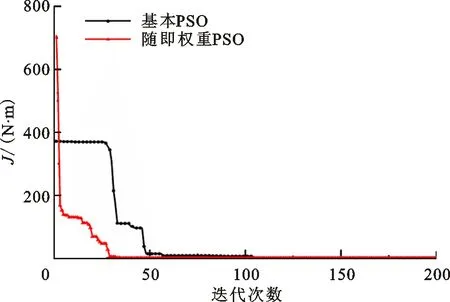
图6 基本PSO与随机权重PSO适应度曲线Fig.6 Fitness curves of basic PSO and random weighted PSO
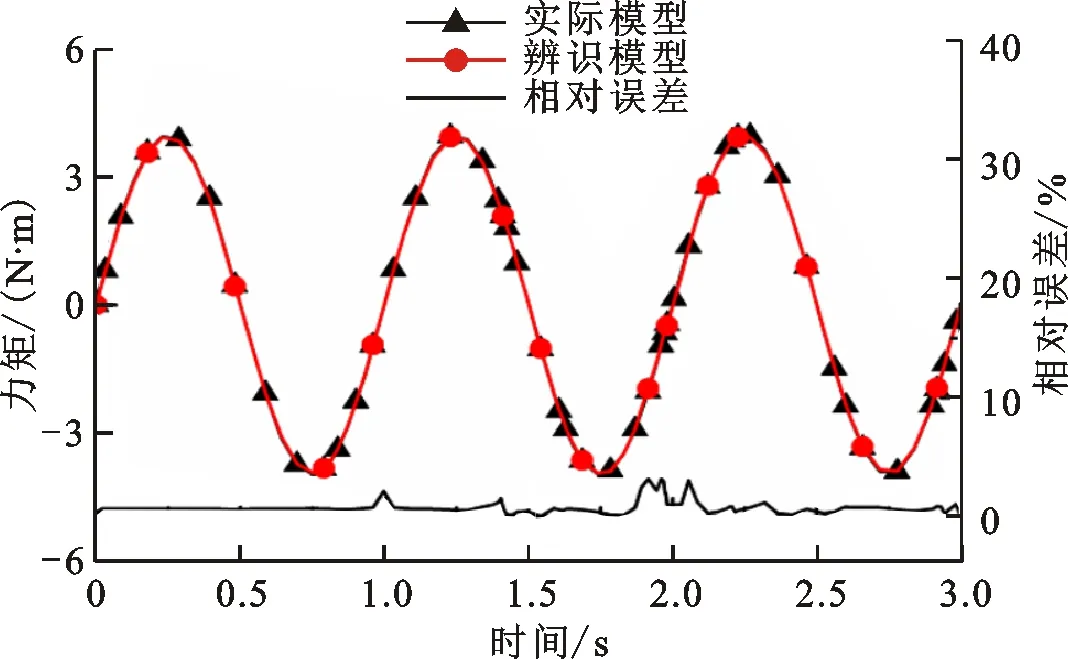
将随机权重PSO辨识出的参数代入式(2),从而得出辨识模型的输出力矩,将其与实际动力学模型输出力矩对比,如图7所示。从图中可以看出,关节1实际模型与辨识模型相对误差控制范围在0~3.5%,关节2实际模型与辨识模型相对误差控制范围在0~4%。因此,采用随机权重PSO辨识出的力矩曲线与实际输出力矩曲线基本吻合,说明该辨识算法有较高的精确性。
(a)关节1

(b)关节2图7 随机权重PSO辨识模型与实际模型输出力矩 Fig.7 Output torque of PSO identification model with random weight and actual model
(a)关节1
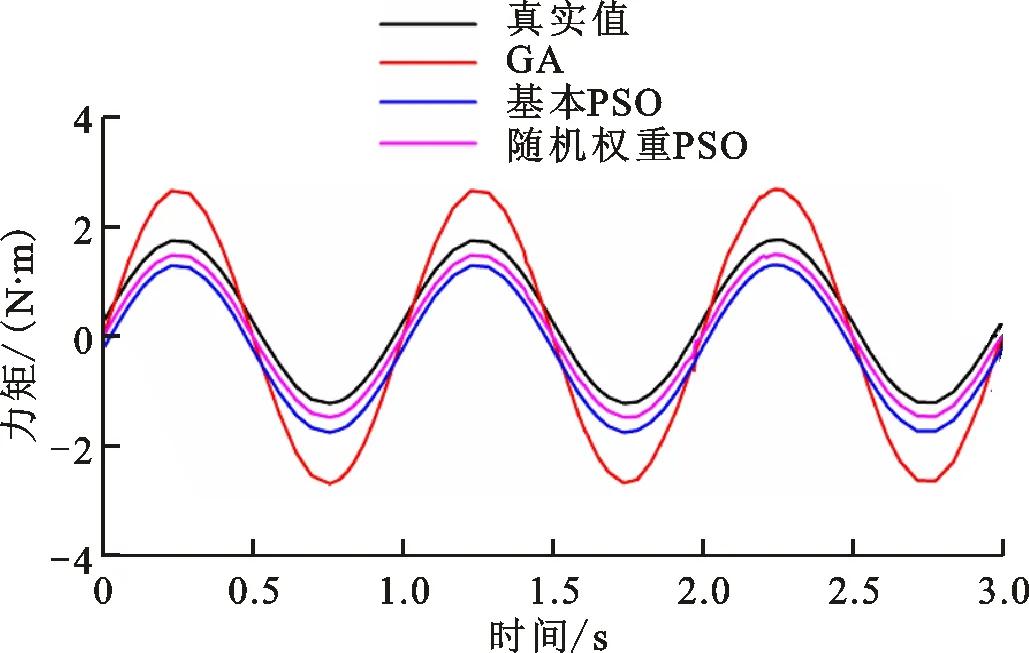
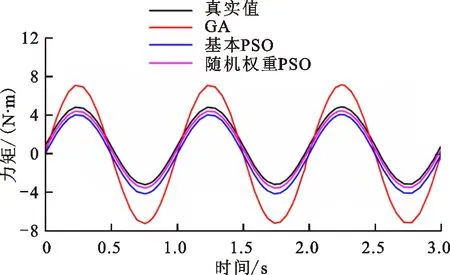
(b)关节2图8 不同算法机器人两个关节力矩辨识值比较Fig.8 Comparison of torque identification values of two robot joints based on different algorithms
为了对比随机权重PSO对参数辨识的精确度,分别将遗传算法、基本粒子群算法、随机权重粒子群算法辨识出的力矩与实际输出力矩进行对比,如图8所示。在遗传算法中,输入信号为式(19),适应度函数为式(20)。仿真实验通过多次调试遗传算法的交叉概率因子和变异概率因子,获取结果最优时的交叉和变异因子分别为0.9和0.2。由图8可以看出:遗传算法的辨识结果整体误差较大,基本PSO与随机权重PSO辨识的结果与实际力矩线误差小。通过仿真实验可得,随机权重粒子群算法辨识的模型与实际模型最接近,误差较小,相比较于其他两种算法更能体现其优越性。
为了进一步比较3种算法的辨识精度,文中引入均方根误差λ来评价所辨识模型的有效性
(21)
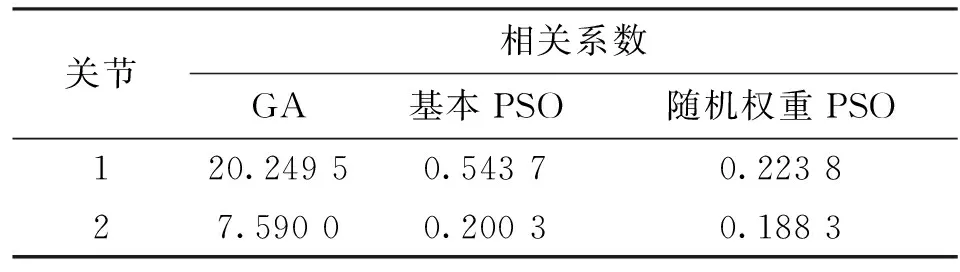
表2 3种算法辨识的关节力矩均方根误差
采用遗传算法、基本粒子群算法、随机权重粒子群算法得到的辨识参数如表3所示。由表3可知,遗传算法辨识的模型参数误差较大,基本PSO与随机权重PSO对模型的辨识精度较高,但采用随机权重PSO辨识得到的适应度函数最优值最小,说明该算法不易陷入局部最优,便于全局搜索,有益于提高参数辨识的精度。
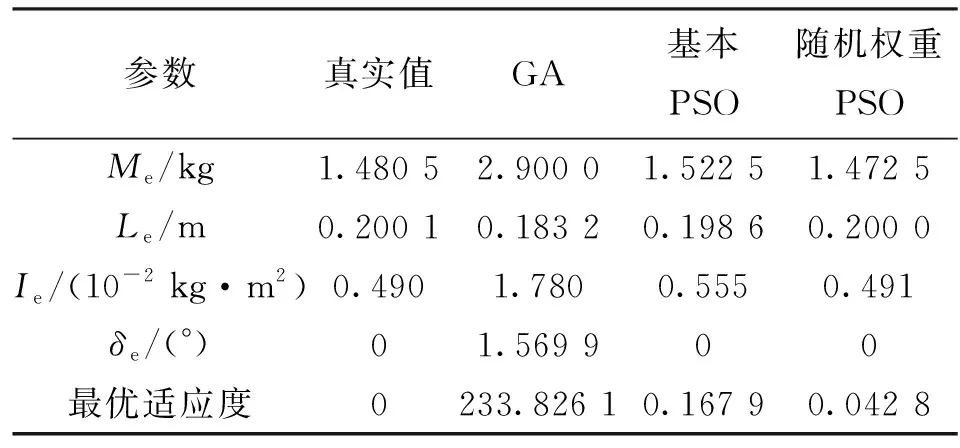
表3 3种算法参数辨识结果对比
4 结 论
本文在分析负载对各关节力矩影响的基础上,将SCARA机器人第3、4关节与未知负载相结合并固联在第2关节上进行动力学建模。在传统粒子群算法的基础上,提出一种随机权重PSO对机器人动力学参数进行参数辨识。仿真实验结果表明,该改进算法收敛速度快、寻优能力强、辨识精度高,与GA、基本PSO相比,辨识精度有明显提高,有助于提高机器人轨迹控制的精度和稳定性。

