三支概念格中的关联规则提取算法

刘美玉,祁建军,刘伟

(西安电子科技大学计算机科学与技术学院,710071,西安)

自Agrawal等首次从大型数据库中提取出关联规则[1]以来,关联规则的提取已成为数据挖掘领域中的重要内容。关联规则可以在大量的数据中揭示特征与特征之间的隐含关系,从而达到数据挖掘的目的。

关联规则表示属性集之间的相关性。在形式概念分析(FCA)[2]中,概念表示对象集和属性集之间的统一,概念格节点之间的关系表示概念的泛化和例化。因此,概念格是非常适合关联规则提取的工具之一。目前,已有一些利用概念格进行关联规则发现的方法。Zaki等提出CHARM算法,利用概念格闭项集的特性和对概念格的深度优先搜索提取了非冗余的关联规则[3];Stumme等提出TITANIC算法,通过对概念格进行改造,提高了关联规则挖掘的效率[4];Kim等设计了一个完整的关联规则挖掘系统FARM,该系统将关联规则与植物的生长模型联系起来,依据布尔表达式生成只与用户兴趣相关的关联规则,与CHARM算法和TITANIC算法相比,FARM有更优的效果[5]。在国内:谢志鹏等首先发现了概念格在关联规则提取上的优势,提出了概念格节点内涵缩减概念,给出了相应的渐进式生成算法和基于概念格的关联规则提取算法[6-8];Wang等利用领域知识来指导概念格上的关联规则挖掘[9];王志海等基于概念格的闭项集特性,提出了一种更有利于规则提取的格结构,并给出了闭标记格中的规则提取算法[10]。从前人的工作中可以总结出,利用FCA提取规则的优点是只提取最大规模的频繁项集,从而缩小了搜索空间,减少不必要的挖掘,从整体上提高了效率。另外,使用闭项集还可以减少规则的冗余。然而,这些方法主要研究了属性子集之间的“具有”关系,即正相关,忽略了属性子集之间的“不具有”关系,即负相关。

Brin等首次提出了负关联的概念,负关联规则描述了两个项集之间的反作用,即某个项集的发生会降低另外某个项集发生的概率[11]。此后,基于FCA进行负规则提取的研究也有了进一步发展。Rodriguez-Jimenez等在建格算法NextClosure的基础上提取了混合属性蕴含[12];Missaoui等根据原形式背景和补背景,提出了一种混合蕴含的提取方法[13]。这些研究仅关注了项集之间的蕴含,并未提取出完整的负规则。

为了更完整地表达形式背景中的信息,Qi等结合三支决策[14]和形式概念分析提出了三支概念分析(3WCA)[15]。三支概念分析是一种进行知识表示与知识发现的理论,可以同时表达“共同具有”和“共同不具有”两种语义,相较于形式概念分析,三支概念分析蕴含了更加丰富的信息。目前,基于三支概念分析理论的研究有了丰富的成果[16-24]。为了获取规则方面的知识,许多学者进行了深入的研究:文献[20]给出了决策形式背景上基于属性导出三支协调性和对象导出三支协调性的规则提取,并与强协调决策形式背景的规则进行了比较;文献[23-24]给出了决策形式背景在属性导出三支概念格下的规则提取方法,在三支概念框架下提出了负规则。这些研究都是基于决策形式背景进行的。

本文以形式背景作为原始数据信息,基于三支概念分析理论对关联规则的提取进行研究,提出基于三支概念分析的关联规则提取算法(3ARM)。该算法从对象导出概念格中概念之间的父子关系和兄弟关系出发,同时提取正关联规则与负关联规则,获得更丰富的知识。

1 三支概念分析

三支概念格是三支概念分析的主要内容,三支概念格包括对象导出(OE)概念格和属性导出(AE)概念格。本文主要在OE概念格上进行研究,因此只介绍OE概念格的相关理论。

定义1[2]形式背景是一个三元组(G,M,I),其中:G={x1,x2,…,xn},每一个xi(i≤n)被称为一个对象;M={a1,a2,…,am},每一个aj(j≤m)被称为一个属性。对于x∈G与a∈M,如果对象x拥有属性a,记为xIa,即(x,a)∈I。

定义2[2]设(G,M,I)为一个形式背景,对于任意的对象子集X⊆G和属性子集A⊆M,一对算子被定义为

*:P(G)→P(M),X*={a∈M|∀x∈X,
(x,a)∈I}

*:P(M)→P(G),A*={x∈G|∀a∈A,
(x,a)∈I}

式中P(·)表示幂集。该算子定义为正算子。

定义3[2]设(G,M,I)为一个形式背景,X⊆G,A⊆M。若二元组(X,A)满足X*=A且A*=X,则称(X,A)为(G,M,I)一个形式概念,简称概念。X称为(X,A)的外延,A称为(X,A)的内涵。

定义4[15]设(G,M,I)为一个形式背景,对于任意的对象子集X⊆G和属性子集A⊆M,一对负算子被定义为

式中Ic=(G×M)-I,×为笛卡尔积。

文献[15]中同时考虑正算子和负算子,从对象子集与属性子集之间“共同具有”和“共同不具有”两个角度出发,给出如下三支算子的定义。

定义5[15]设(G,M,I)为一个形式背景,对于任意的对象子集X,Y⊆G和属性子集A,B⊆M,一对对象导出三支算子定义为

式中DP(·)=P(·)×P(·)。该算子简称为OE算子。

定义6[15]设(G,M,I)为一个形式背景,如果X<·=(A,B)与(A,B)·>=X同时成立,则称(X,(A,B))为(G,M,I)的一个对象导出三支概念,简称OE概念,X称为(X,(A,B))的外延,(A,B)称为(X,(A,B))的内涵。

对于(X,(A,B))和(Y,(C,D)),定义偏序关系为(X,(A,B))≤(Y,(C,D))⟺X⊆Y⟺(A,B)⊇(C,D)。

用OEL(G,M,I)表示由形式背景(G,M,I)生成的所有OE概念的集合,则OEL(G,M,I)在定义6的偏序关系“≤”下是一个完备格,称为(G,M,I)的对象导出三支概念格,简记为OE概念格。其中,上确界和下确界分别为(X,(A,B))∨(Y,(C,D))=((X∪Y)·><·,(A,B)∩(C,D))和(X,(A,B))∧(Y,(C,D))=(X∩Y,((A,B)∪(C,D))·><·)。

用(X,(A,B))<(Y,(C,D))表示(X,(A,B))≤(Y(C,D))且(X,(A,B))≠(Y,(C,D))。如果(X,(A,B))<(Y,(C,D))成立,且不存在使得(X,(A,B))<(Z,(E,F))<(Y,(C,D))成立的(Z,(E,F)),则称(X,(A,B))是(Y,(C,D))的子概念,(Y,(C,D))是(X,(A,B))的父概念,记为(X,(A,B))(Y,(C,D))。

例1 表1表示形式背景(G,M,I),表中G={1,2,3,4},M={a,b,c,d,e},○表示对象具有属性,空表示对象不具有属性。图1为(G,M,I)对应的OE概念格OEL(G,M,I),图中概念外延和内涵都以罗列的元素序列来表示相应集合,如123表示{1,2,3}。

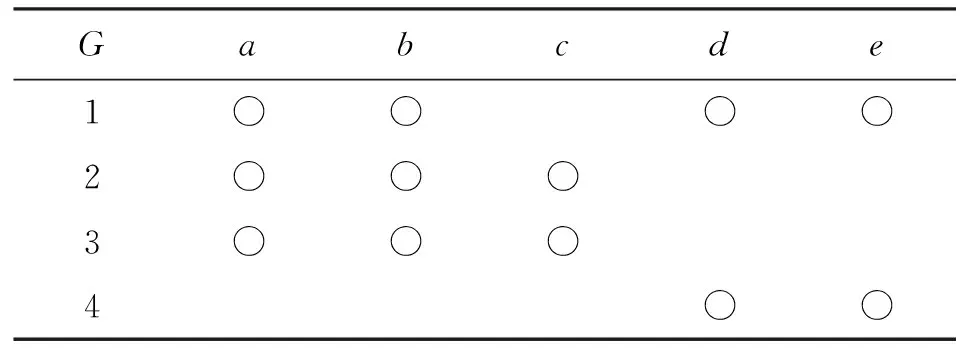
表1 形式背景(G,M,I)

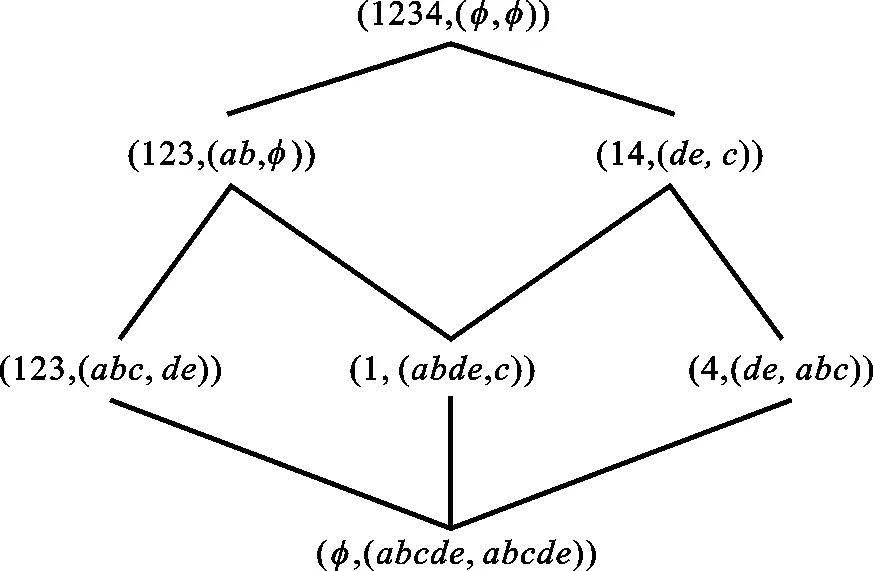
图1 OEL(G,M,I)Fig.1 OEL(G,M,I)

在OEL(G,M,I)中,凡是有边直接相连的两个概念就是一对父子概念。同一个父概念的两个子概念是一对兄弟概念。

2 三支概念格中的关联规则提取

关联规则是形如A⟹B的规则,其中A和B为项的集合。任意项集X的支持度是包含X的事务在事务集D中所占百分比,记为supp(X)=|X(t)|/|D|,其中X(t)={D中事务t|t包含X}。支持度大于给定的最小支持度的项集称为频繁项集。关联规则A⟹B的支持度supp(A⟹B)=supp(A∪B),即包含A∪B的事务在事务集中所占百分比。关联规则的置信度conf(A⟹B)=supp(A∪B)/supp(A),即事务集中包含A的事务同时包含B的百分比。

挖掘关联规则的目标是生成所有支持度大于给定的最小支持度s且置信度大于最小置信度c的关联规则。一般包括计算所有的频繁项集、从频繁项集中生成置信度大于最小置信度的关联规则两步。本文依据这一思想,对三支概念格进行剪枝,选出候选概念,再根据候选概念间的父子关系和兄弟关系提取出符合条件的关联规则。

在形式概念分析中,形式背景(G,M,I)可以理解成事务数据库,其中G为数据库中事务的集合,M为数据库中所有可能项的集合。对于x∈G与a∈M,xIa则表示a属于事务x的项集,那么项集之间的关系在概念格中就得到了充分的体现,每个概念就是一个最大频繁项集。概念(X,A)中,X是全体事务集的子集,A是这些事务共同具有的闭项集。一条关联规则A⟹B成立,对应于内涵包含A的概念同样包含B。

定义7设(G,M,I)为一个形式背景,A,B,C,D⊆M,正规则A⟹B的支持度定义为具有A∪B的对象在G中所占的比例,记为

定义8设(G,M,I)为一个形式背景,A,B,C,D⊆M,正规则A⟹B的置信度定义为具有A∪B的对象在具有A的对象中占的比例,记为

(2)如果有(X,(A,B))(Y,(C,D)),则可以得到正规则C⟹A-C和负规则D⟹(B-D);

(3)如果同时满足(X,(A,B))(Z,(E,F))且(Y,(C,D))(Z,(E,F)),则可以得到正规则A⟹C-A∩C和负规则B⟹(B-B∩D)。

根据这3步,给出基于三支概念分析的正负关联规则提取算法,即3ARM算法,具体如下。

3ARM算法:从OEL(G,M,I)中提取正负关联规则

输入:OEL(G,M,I),s,c

输出:正规则集合R+、正规则对应的支持度集合S+和置信度集合C+,负规则集合R-、负规则对应的支持度集合S-和置信度集合C-

1 for (X1,(A1,B1)) in OEL(G,M,I):

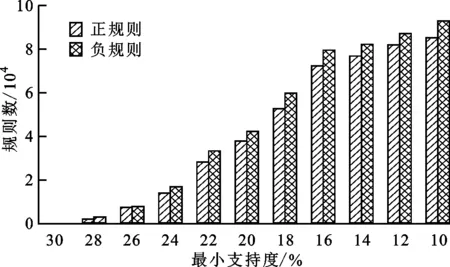
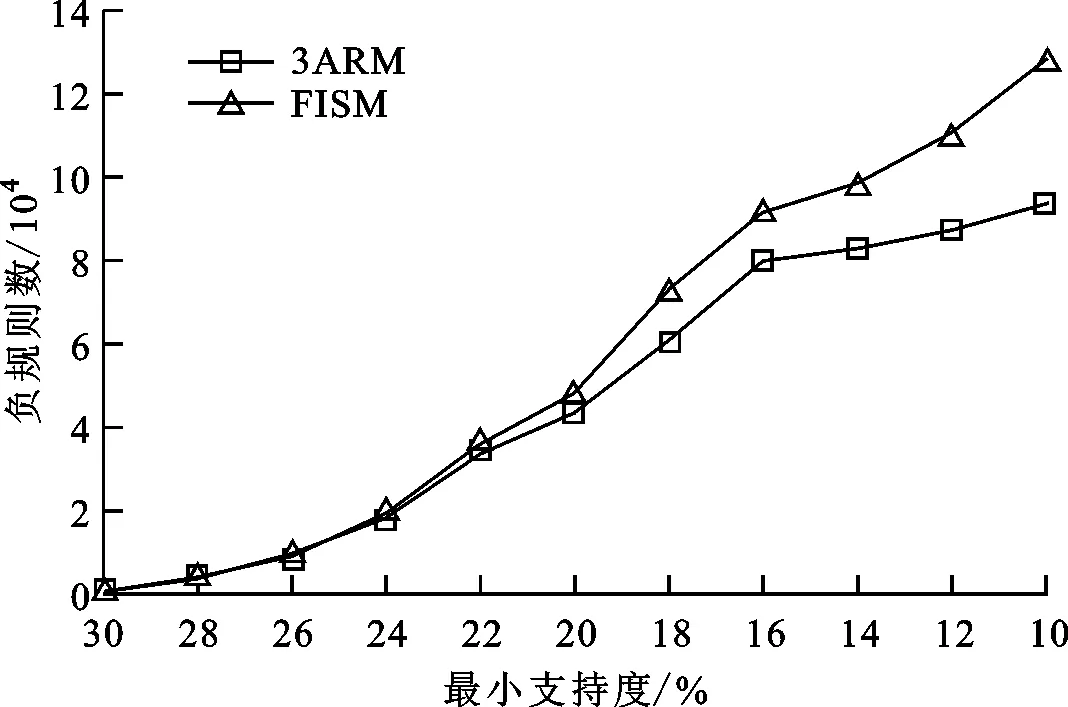
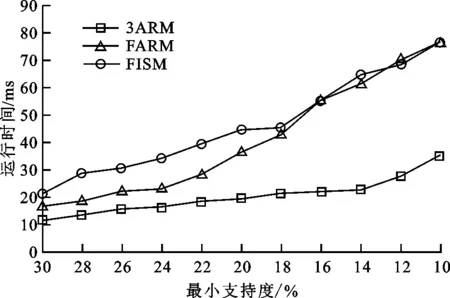
2 if |X1|

3 continue

9 for (X2,(A2,B2)) in (X1,(A1,B1)).Parent-concepts:

10 if supp(A2⟹A1-A2)>sand conf(A2⟹A1-A2)>cthen

11 putA2⟹A1-A2intoR+

12 put supp(A2⟹A1-A2) intoS+

13 put conf(A2⟹A1-A2) intoC+

18 for (X3,(A3,B3)) in (X2,(A2,B2)).Child-concepts:

19 if (X3,(A3,B3))≠(X1,(A1,B1)) then

20 if supp(A1⟹A3-A1∩A3)>sand

conf(A1⟹A3-A1∩A3)>cthen

21 putA1⟹A3-A1∩A3intoR+

22 put supp(A1⟹A3-A1∩A3) intoS+

23 put conf(A1⟹A3-A1∩A3) intoC+

intoS-

intoC-

28 returnR+,S+,C+,R-,S-,C-

步骤1～3:设置循环体,选择候选概念(X1,(A1,B1))。

步骤4～8:从概念(X1,(A1,B1))的内涵中提取负关联规则。

步骤9～13:提取(X1,(A1,B1))和父概念之间的正关联规则,并根据定义7和8计算正规则的置信度和支持度。

步骤14～17:提取(X1,(A1,B1))和父概念之间的负关联规则,并计算负规则的置信度和支持度。

步骤18～23:设置循环体,此时(X2,(A2,B2))是(X3,(A3,B3))和(X1,(A1,B1))的公共父概念,提取(X1,(A1,B1))和兄弟概念(X3,(A3,B3))之间的正关联规则,计算两个正规则的置信度和支持度。

步骤24～27:提取(X1,(A1,B1))和兄弟概念(X3,(A3,B3))之间的负关联规则,并计算两个负规则的置信度和支持度。

在第二层循环结束时,关于概念(X1,(A1,B1))生成的规则提取完毕。另外,从算法中可以分析得出,随着最小支持度和最小置信度的增大,候选概念的数量减少,规则的数量随之减少,程序运行的时间也随之减少,然而对非候选概念的判断相对增多,使得整体效率略微降低。

例2 根据3ARM算法,s=c=0.4时,例1中OEL(G,M,I)得到关联规则如表2所示。

表2 关联规则及其支持度和置信度

规则1～5由概念间的父子关系得到,负规则6～9由单个概念生成。特别的,前件为空集的规则,如规则1、2、4、5,可以根据实际应用选择保留或者删除。例如,在推荐系统中,这些规则可以用作为新用户提供推荐的依据,而后件为空集的规则一般被忽略。

3 实验及分析

实验数据采用推荐系统中广泛使用的MovieLens数据集。数据集组成为:User(userID,age,gender,occupation),Movie(movieID,title,genres,tag),Rating(userID,movieID,rating,timestamp)。其中,Rating含有610个用户对9 742部电影的100 836个评分。

3.1 正规则分析

首先,把评分信息转化成形式背景,建立OE概念格和经典概念格。OE概念格分析得到的概念数和父子概念对数分别为13 583、137 229,经典概念格的分别为10 787、87 984。可以看出,在相同的形式背景下,OE概念格中的概念数和父子概念对数均大于经典概念格中的。

然后,对3ARM算法提取到的关联规则与其他算法取得的规则进行数量上和分布上的分析。3ARM算法得到的关联规则中正负规则的分布情况如图2所示。可以看出,得到的正规则数量占全部规则数量的25%～42%,负规则数量占全部规则数量的58%～75%,是正规则的1.06倍～1.26倍。

图2 3ARM算法得到的正负规则分布情况Fig.2 Positive and negative rules distribution from 3ARM

3ARM算法与FARM算法提取出的正规则数对比如图3所示。可以看出,两种算法得到的正规则都主要分布在支持度小于30%的范围内,且在同一最小支持度阈值下,3ARM算法得出的正规则数量比FARM算法得出的规则数量多出0.9～1.5倍。综合分析可知,概念间父子关系数的增多是使得3ARM算法得到更多正规则的主要原因。

图3 3ARM算法与FARM算法得到的正规则数对比Fig.3 Comparision of positive rules between 3ARM and FARM

3.2 负规则分析

为评估提取到的负规则的可靠性,对3ARM算法与FISM算法进行对比。FISM算法是Balakrishna等提出的一种基于频繁项集的负关联规则提取算法,利用改进的FP-tree生成频繁项集,再从频繁项集中生成负规则[26]。3ARM算法与FISM算法得到的负规则数对比如图4所示。可以看出:支持度为22%～30%时,3ARM算法与FISM算法提取到的负规则数量相当;随支持度减小,3ARM算法提取到的负规则数量逐渐少于FISM算法的,且差距逐渐拉大。将两种算法提取到的规则进行对比,可以发现FISM算法提取到的规则中存在类似于的冗余规则,而3ARM算法利用三支概念的优势,从最大频繁闭项集的泛化与例化关系中提取负规则,大量减少了冗余规则的生成。

图4 3ARM算法与FISM算法得到的负规则数对比Fig.4 Comparision of negative rules between 3ARM and FISM

3.3 运行时间分析

对3ARM算法、FARM算法和FISM算法的运行时间进行对比,实验结果如图5所示。需要说明的是,这里的运行时间指的是在概念格上提取关联规则的时间,不包括构建经典格和OE概念格的时间,3ARM算法的运行时间是同时提取正规则和负规则所需时间。为保证公平性,FISM算法的运行时间也不包含生成FP-tree所需的时间,而实际上,3ARM算法对数据库进行一次扫描就可以建立OE概念格,构建FP-tree则需要两次扫描数据库。

图5 3ARM、FARM及FISM算法的运行时间对比Fig.5 Comparison of running time of 3ARM,FARM and FISM

从图5可以看出,3ARM算法的运行时间明显小于FARM算法和FISM算法的。在同一支持度阈值下,3ARM算法的运行时间比FISM算法减少了44%～63%,比FARM算法减少了27%～62%。与FARM算法相比,3ARM算法省去了布尔表达式的逻辑运算;与FISM算法相比,3ARM算法省去了将频繁项集两两结合生成负规则的时间。3ARM算法利用OE概念格的偏序关系及OE概念闭项集的特性,有规律地提取关联规则,提高了算法的效率。

从第3节实验可以得出,与FARM算法相比,3ARM算法不仅可以延续经典概念格提取非冗余正规则的优点,还可以提取出有价值的负规则。与FISM算法对比,3ARM算法可以减少负规则的冗余。从运行时间上看,3ARM算法减去了复杂的操作,缩短了算法的运行时间。

4 结 论

在关联规则的提取方面,现有许多基于概念格进行正规则提取的研究,取得了较好的效果,并在文本分类[18]、推荐系统[27-28]等领域有充分的应用。为更完整地提取关联规则,本文提出基于三支概念分析的关联规则提取算法3ARM,利用三支概念的闭项集特性,从父子关系和兄弟关系中提取了具有置信度和支持度的正关联规则和负关联规则。经过实验对比和分析,得出结论如下。

(1)在同一形式背景上,建立的三支概念格比经典概念格包含更多的概念和父子关系,因此3ARM算法能比FARM算法提取到更多的正规则。

(2)利用三支概念的闭项集特性,能快速得到最大规模的频繁项集,减少了冗余规则的产生;利用3WCA中“共同具有”和“共同不具有”的语义,3ARM算法可以同时提取到正规则和负规则。

(3)根据三支概念间的父子关系和兄弟关系,有规律地进行规则的提取,减少了不必要的操作,使得3ARM算法的运行时间少于FARM算法和FISM算法的。

未来将研究本文算法应用于推荐系统。