含多重累加函数的典型爆轰驱动模型不确定度分析方法

沈 飞，王 辉，张 皋

（西安近代化学研究所，陕西 西安 710065）

1 引言

炸药爆轰释能是一个复杂的物理化学过程，其量化研究大多基于试验观测数据进行唯像建模。由于不同炸药的爆轰过程差异较大，试验观测数据的规律性表征常采用特定的多重累加型函数（由多个形式相同的多项式叠加组成）进行回归拟合，如炸药水下爆炸近场的冲击波传播距离随时间变化的曲线［1，2］，稳态爆轰的波阵面形状曲线［3，4］，圆筒试验中的铜管径向膨胀位移随时间变化的曲线等［5，6］。为了进一步获得评价炸药爆轰性能的物理量，常需要对这些拟合曲线进行微分处理，因而建立拟合过程不确定度与其它物理量不确定度之间的关系，这对于整个爆轰模型测量或计算精度的分析十分重要。为了系统地建立该类模型的不确定度分析方法，本研究针对圆筒试验模型进行了相应的不确定度分析。

圆筒试验是研究炸药驱动能力的经典试验，通过狭缝高速扫描摄影法获取定常滑移爆轰驱动下铜管壁的径向膨胀位移随时间的变化曲线，并采用特定的多重累加函数进行拟合，然后进一步计算出铜管膨胀速度、比动能等物理量［6，7］。该试验及分析模型主要包括膨胀位移-时间曲线的数据获取、拟合、微分3个步骤，一些文献［5，7］分析了位移或时间数据点测量不确定度以及曲线拟合参数不确定度的基本计算方法。但现有文献中并未建立各物理量不确定度之间的关系，且所采用的拟合参数不确定度计算方法不能适用于该多重累加拟合函数，因此未能建立铜管膨胀速度、比动能等物理量不确定度的分析方法。

本研究通过在膨胀位移表达式中引入估计值为1的无量纲参量，获得了膨胀位移和膨胀速度两者测量不确定度的关系式，并修正了多重累加函数的拟合参数不确定度分析模型，建立了较为系统的圆筒试验不确定度评定及计算方法。

2 基本原理及原始数据的测量不确定度

2.1 圆筒试验基本原理

炸药圆筒试验的原理如图1所示，将炸药装填在标准尺寸的铜管内，并从铜管的一端起爆炸药，采用狭缝扫描相机观测铜管的某一截面。当相机的转镜高速旋转时，在胶片的不同位置可记录铜管在不同时刻的膨胀状态。

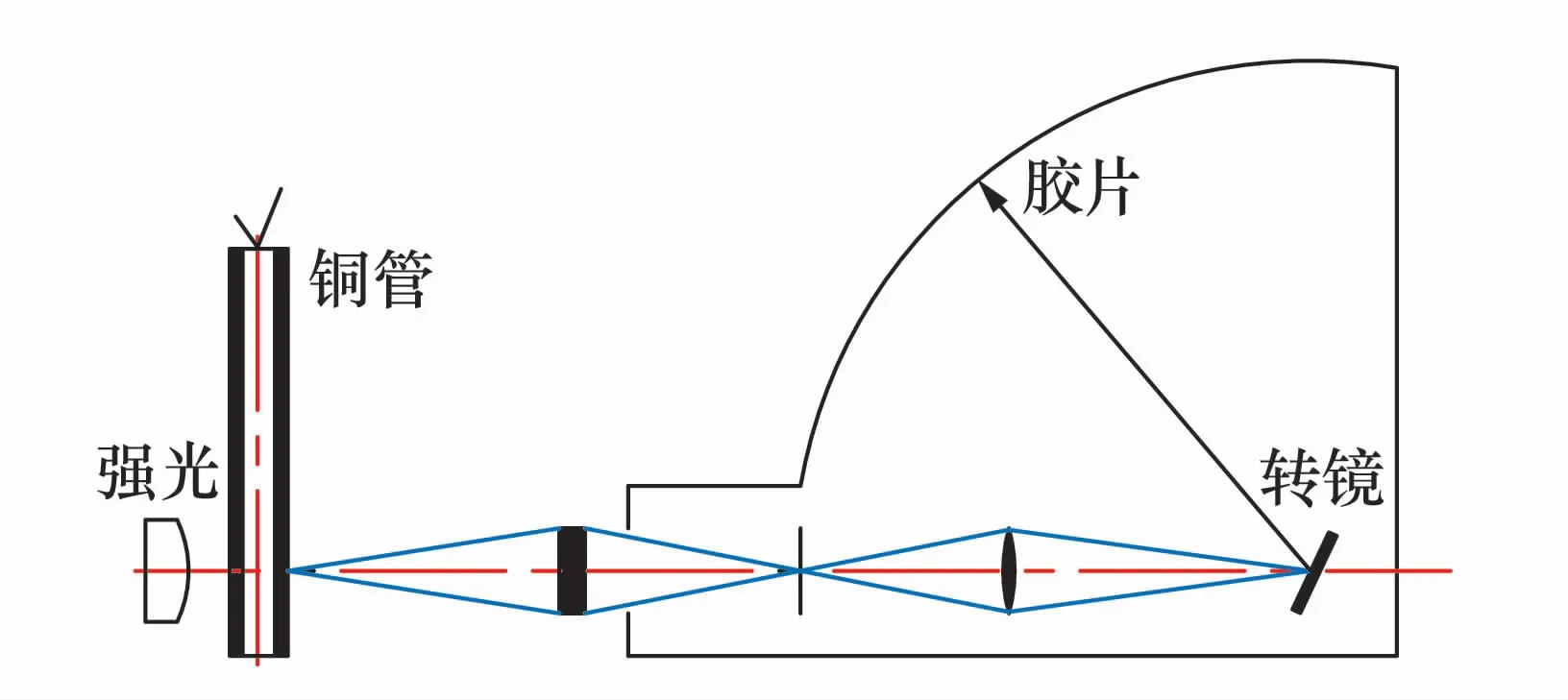
图1 圆筒试验原理示意图Fig.1 Schematic diagram of cylinder test

圆筒试验的原始数据为胶片中的图像边界，如图2所示。其中，横向为转镜扫描光路的线位移，其除以转镜的线速度即为时间值；纵向可反映铜管直径的变化。

图2 圆筒膨胀图像的边界参量示意图Fig.2 Schematic diagram of boundary parameters of cylinder expansion image

2.2 铜管径向位移的测量不确定度

采用高精度扫描仪将胶片图像转换为电子图像，然后由专用判读软件进行边界识别（铜管径向的像位移（yj－y0），对应的横向距离为（xj－x0），其识别的判据为图像灰度梯度是否达到极值。

根据相应的算法分析［8，9］及重复性验证获知，对于2 400 dpi分辨率的图像，采用一阶算法时，边界线的识别偏差为0～2个像素（pixel），即0～0.02 mm，则边界识别的不确定度即为0.02 mm。由于确定两点距离时需判定两个边界，则u（yj－y0）＝u（xj－x0）≈0.03 mm。

综上分析可以发现，铜管外表面的实际径向位移Δrej＝（yj－y0）／β的测量不确定度来源于图像边界识别和放大比测量的随机误差。然而将图像放大比作为一个固定值输入到每一个数据点时，将产生系统误差，并影响后续的拟合、求导等过程。为了便于对该问题进行分析，可将铜管实际径向位移的表达式修改为：

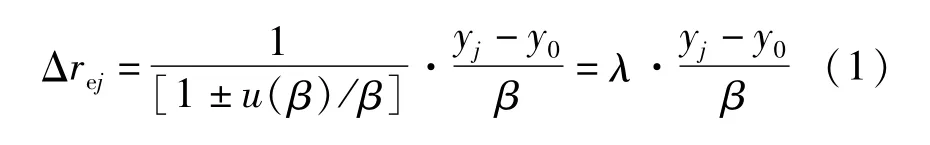
即引入参量λ，其估计值为1，u（λ）≈u（β）／β，对于ϕ25 mm的标准铜管，则u（λ）≈3.5×10－3。

2.3 时间的测量不确定度

由于铜管膨胀时间为tj＝（xj－x0）／v，其中，v为相机的扫描线速度，则

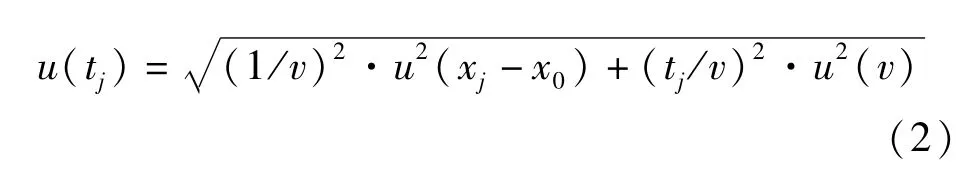
从式（2）可以看出，对于同一发试验，仅有（xj－x0）为变量，u（tj）随（xj－x0）单调递增。文献［7］研究认为，u（v）＝0.001v，则对于ϕ25 mm的标准圆筒试验，当v＝3 mm／μs时，式（2）可简化为：

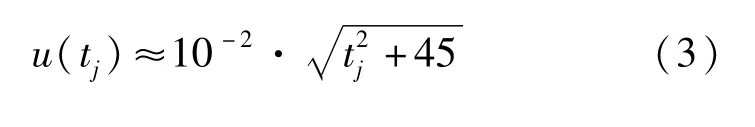
3 位移曲线拟合参数的不确定度

3.1 曲线拟合的基本步骤

目前GJB 8381—2015［5］及国外公开报道的资料［6］中，均首先将铜管外表面膨胀轨迹的判读点（tj，Δrej）按照公式（4）转换为铜管质量中心面处的数据点（tj，Δrmj），

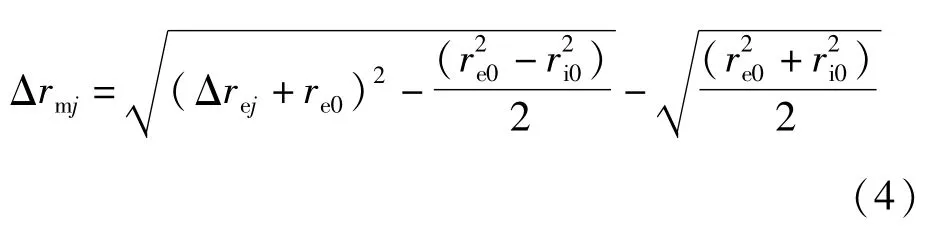
式中：re0和ri0分别为铜管内外表面的初始半径。

由公式（4）和不确定度传递规律可知，u（Δrej）≈u（Δrmj），然后按照公式（5）的形式，利用最小二乘法对数据点（tj，Δrmj）进行拟合，从而获得a1、b1、a2、b2、t0等5个拟合参数。此外，公式（5）为典型多重累加函数，为了便于表示，采用f1和f2分别表示两个多项式。

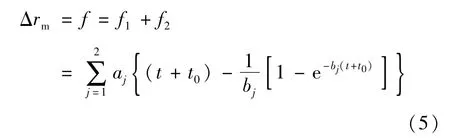
拟合曲线的实验标准偏差可作为拟合曲线的标准不确定度［10］，即

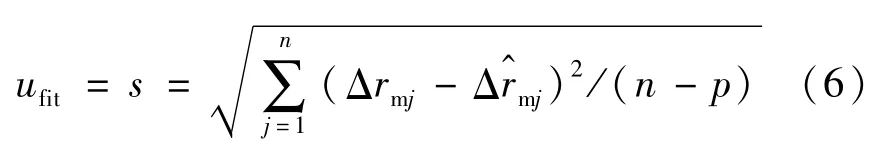
式中：Δrmj和j分别为时间tj所对应的径向位移实验值和拟合值；（n－p）为自由度，n为实验点的总数，p为拟合参数的数量。采用决定系数R2值可作为拟合符合程度的度量。

以TNT和JO-159炸药的某一发ϕ25 mm圆筒试验数据为例进行分析，其结果见表1，由决定系数R2值可看出拟合精度较高。

表1 铜管膨胀位移曲线拟合参数Tab.1 Curve-fitting parameters of the expansion displacement of the cylinder wall

3.2 多重累加函数拟合参数不确定度的模型修正

由于公式（5）为典型弱非线性函数，尤其是当t不断增大后，Δrm近似于线性增长，因此，计算拟合参数的不确定度时，可采用泰勒一阶展开式对其进行近似表示［10］：

式中：y和γ分别为数据点Δrmj及残差组成的向量；β为p个拟合参数所组成的向量；Aij＝

从而可进一步计算出拟合参数的方差—协方差矩阵C＝（ATA）－1，矩阵ATA的元素形式可表示为

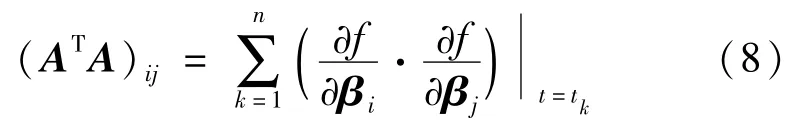
拟合参数βi的标准不确定度为

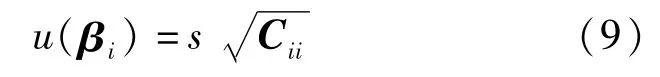
不同拟合参数之间协方差为

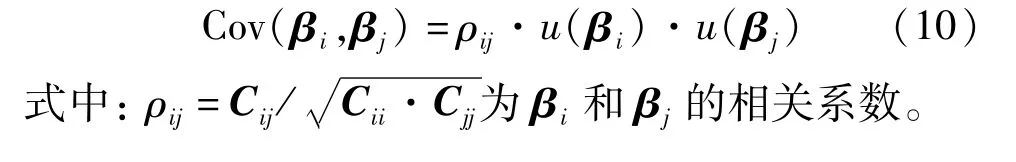
然而，若将公式（5）中的5个拟合参数作为估计量，即β＝［a1b1a2b2t0］T，则采用上述方法计算不确定度时，铜管膨胀轨迹和公式（5）的固有特征会导致两类现象出现，从而造成计算错误。第一类现象，若b1或b2的值较大（为便于描述，这里假定b1的值较大），f1≈a1（t＋t0），膨胀曲线的非线性特征主要由f2描述，则由公式（5）可推导出

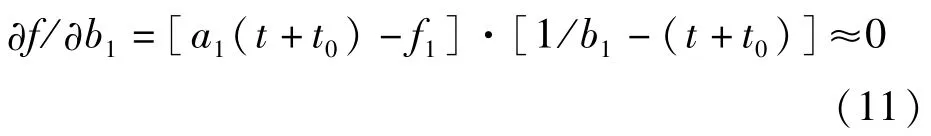
将其代入公式（8）可知，矩阵ATA的第2列及第2行的元素均近似为0，使得该矩阵为奇异矩阵，难以求解其逆矩阵。第二类现象，若b1或b2较为接近，近似于公式（5）中j＝1的情况，使得∂f／∂a1≈∂f／∂a2，从而造成ATA矩阵的两行或两列数据相近，即近似为奇异矩阵，仍难以求解其逆矩阵。

对于复杂非线性函数造成的不确定度计算困难，虽然从蒙特卡罗方法中可能会寻求出相应的解决途径［11～13］，但在后续的求导等计算过程中将会出现新的问题，因此，本研究中仍基于传统GUM不确定度评定方法进行分析。结合公式（5）所示的多重累加回归模型的特点可以发现，虽然f1和f2一般是同时进行拟合计算的，但本质上这两个多项式的拟合过程可以分步进行。第一步，采用Δrm＝f1（t）对实验数据点（tj，Δrmj）进行拟合，可获得a1、b1、t0这3个参数值，并计算出每个数据点的残差（tj，Δrmjf1（tj））；第二步，将（tj，Δrmj－f1（tj））数据点代入Δrm－f1（t）＝f2（t）进行拟合，获得a2、b2两个参数值。可以看出，最终残差值由第二步拟合的精度决定，因此，可认为a1、b1、t0的值为真值，而a2、b2的值为估计值，并分析这两个拟合参数的不确定度。设β＝［a2b2］T，则ATA矩阵的具体形式为

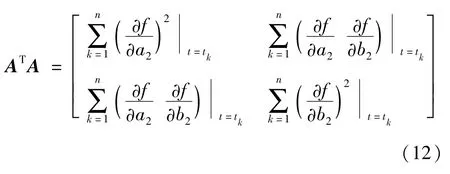
式中：

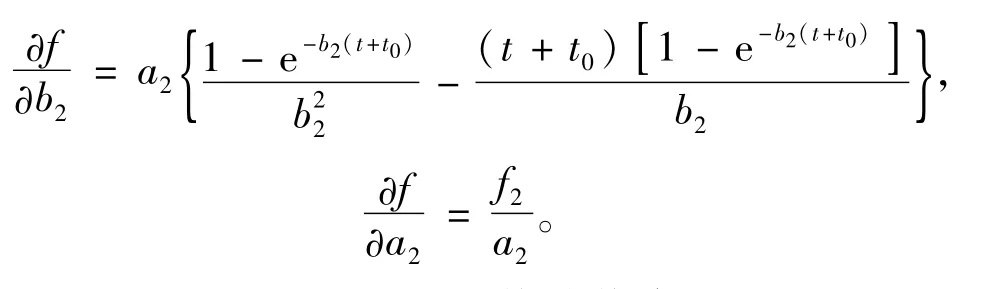
需要说明的是，选择估计值参量时，a1、b1和a2、b2可以互换。

根据式（9）、式（10）、式（12），并结合表1所列数据，可计算出两种炸药的拟合参数的不确定度，具体数值见表2。

表2 拟合参数的标准不确定度Tab.2 Uncertainty evaluation of curve-fitting parameters

4 铜管速度及比动能的不确定度

4.1 铜管径向膨胀速度的测量不确定度

将公式（5）对时间t求导，并结合公式（1），可得到铜管的径向膨胀速度vm：

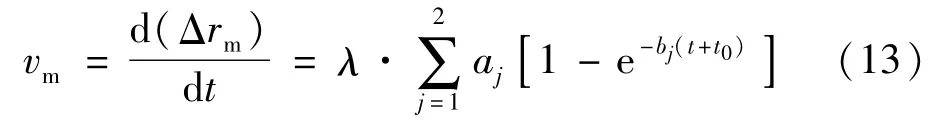
则vm的标准不确定度为

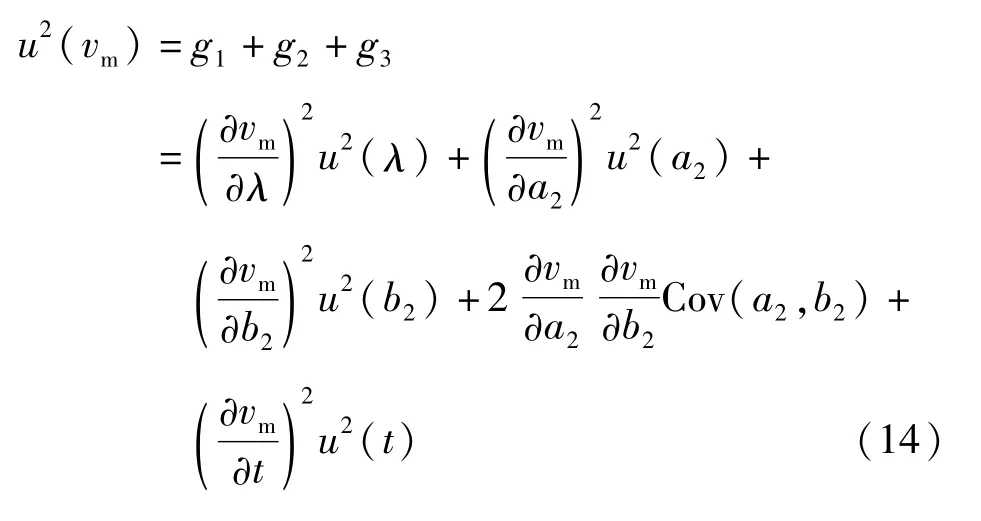
式中：g1、g2、g3分别表示图像放大比、拟合参数、膨胀时间的相关多项式。

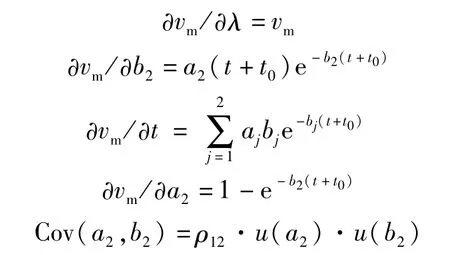
为了弄清这3类因素对u（vm）的影响程度，可基于表1中的数据对ω（λ）＝g1／u2（vm）、ω（a2，b2）＝g2／u2（vm）、ω（t）＝g3／u2（vm）的变化规律进行分析，结果如图3所示。

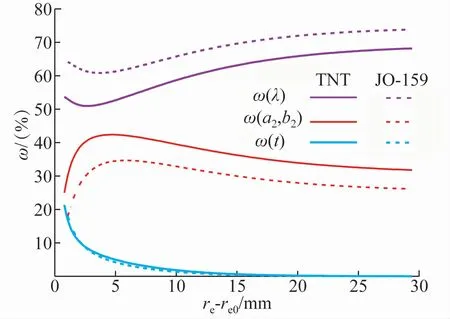
图3 不同因素对铜管径向速度不确定度的影响规律Fig.3 The influence of different factors on the uncertainty of the radial velocity of copper pipe

由图3可以看出：对于TNT和JO-159两种不同作功能力的炸药，u（λ）（即图像放大比的相对标准不确定度u（β）／β）对u（vm）的影响均最大，且随着铜管膨胀位移的增大，其影响程度逐渐增大，而拟合参数和膨胀时间的不确定度对其影响程度逐步减弱，尤其是在膨胀后期，膨胀时间不确定度的影响基本可以忽略；对于JO-159炸药，u（λ）对u（vm）的影响程度高于TNT，而拟合参数不确定度对u（vm）的影响程度低于TNT。因此，在圆筒试验测量过程中，对图像放大比的测量精度应更为重视。

4.2 圆筒比动能的测量不确定度

获得圆筒比动能时，首先需要计算出铜管质量中心面的质点速度vs，即

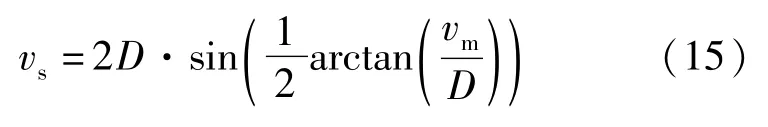
式中：D为炸药在铜管中的爆速，可通过铜管首、尾端设置的电探针同步测量，TNT和JO-159的爆速分别为6.830 mm／μs和8.760 mm／μs。

根据国军标GJB 772A-1997［14］可计算出TNT和JO-159爆速的测量不确定度u（D）分别为0.010 mm／μs和0.016 mm／μs。由公式（15）可获得vs的标准不确定度计算式为

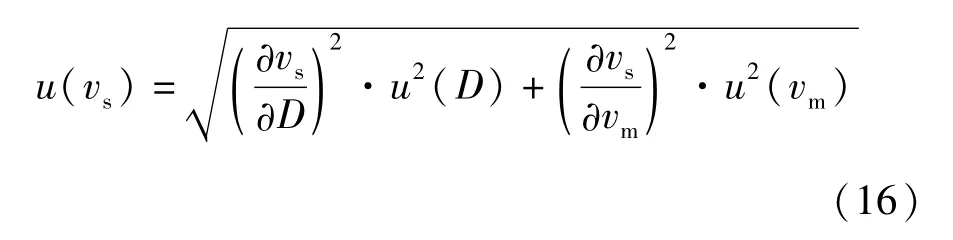
式中：

取包含因子k＝2，置信水平约0.95，则圆筒比动能E的相对扩展不确定度为：

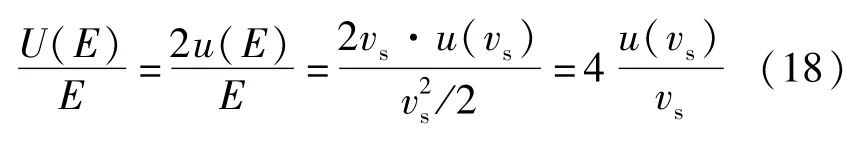
基于上述分析模型，可对TNT和JO-159炸药的ϕ25 mm圆筒径向膨胀速度vm和比动能E的测量不确定进行分析，结果如图4所示。

由图4（a）可以看出：对于这2种炸药，u（E）与E近似呈线性关系，在铜管膨胀后期，u（E）随E的增长速率逐渐变缓；在铜管膨胀过程中（忽略膨胀初期），JO-159炸药的E及u（E）均高于TNT。图4（b）显示了比动能E的相对扩展不确定度U（E）／E（k＝2）的变化曲线，由图可以看出：随着E的增大，U（E）／E均呈现先增大（主要在膨胀早期）后减小的趋势；JO-159的U（E）／E值变化范围为1.60%至1.75%，而TNT的U（E）／E值变化范围为1.67%至1.93%。因此，对于作功能力较强的炸药，其U（E）／E值低于作功能力低的炸药。此外，由于这两种炸药具有较强的代表性，可以预测，对于大多数高能炸药的ϕ25 mm圆筒试验，其圆筒比动能的相对扩展不确定度不超过2%。

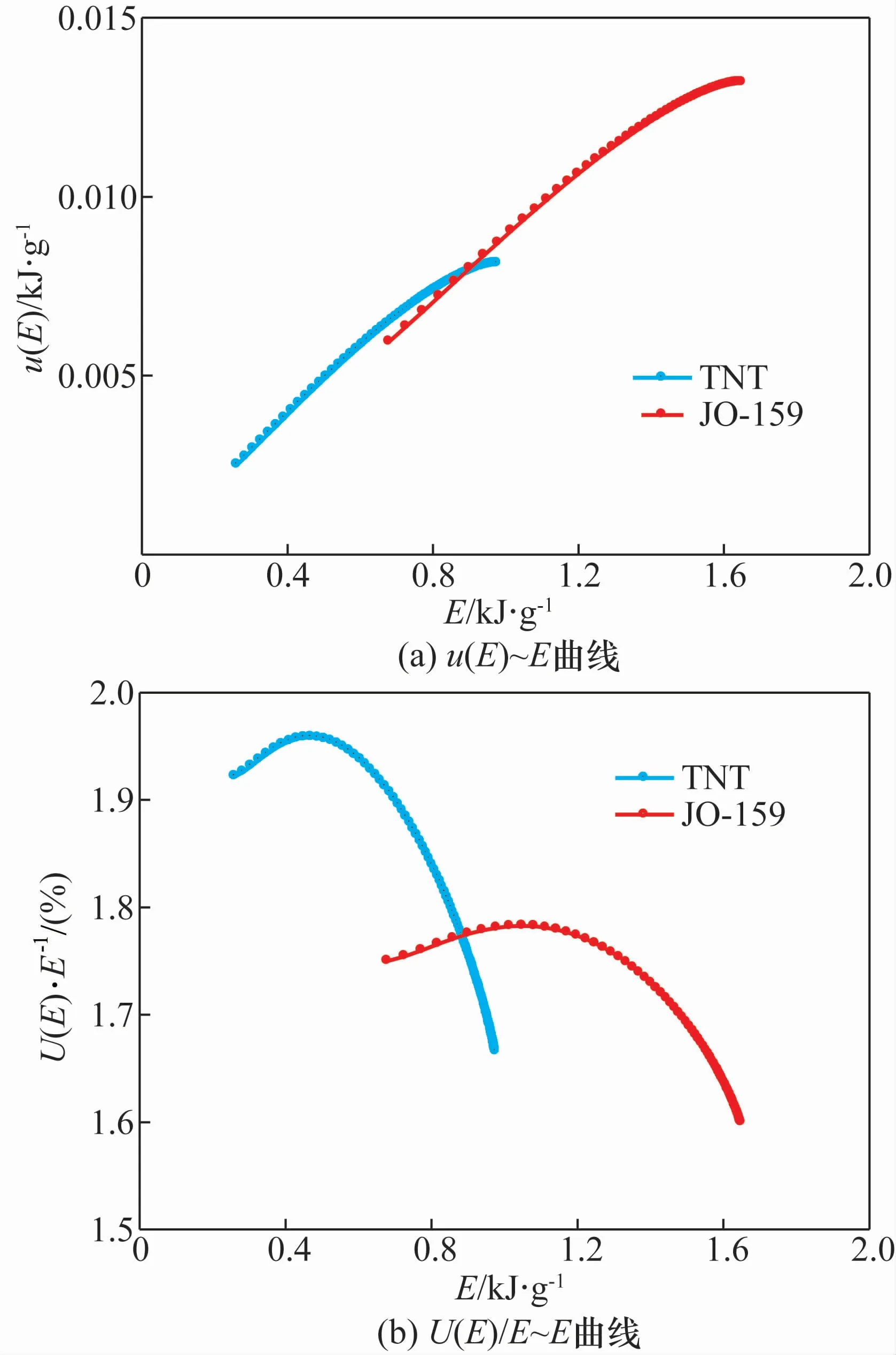
图4 圆筒比动能的不确定度变化曲线Fig.4 Uncertainty curve of specific kinetic energy of cylinder

5 结论

（1）对于含多重累加拟合函数的爆轰模型，分析其拟合参数的不确定度时，应选择影响最终拟合残差值的部分参数作为估计值，从而可避免因出现奇异矩阵而导致的计算错误。

（2）铜管膨胀速度及比动能测量不确定度的最大影响因素是图像放大比的相对不确定度，其次为膨胀曲线拟合参数的不确定度，而膨胀时间的不确定度对其影响最小。

（3）随着圆筒比动能的增大，其标准不确定度近似呈线性增长趋势，而相对不确定度则呈现先增大（主要在膨胀早期）后减小的趋势；且对于作功能量较强的JO-159炸药，其圆筒比动能的相对不确定度明显低于TNT。此外，根据这2种典型炸药的分析结果可以预测，对于大多数高能炸药的ϕ25 mm圆筒试验，其圆筒比动能的相对扩展不确定度（k＝2）不超过2%。