重载并联六维力传感器及静态标定

蔡大军，姚建涛，李颖康，易旺民，许允斗，赵永生

（1.燕山大学 河北省并联机器人与机电系统实验室，河北 秦皇岛 066004；2.燕山大学先进锻压成形技术与科学教育部重点实验室，河北秦皇岛 066004；3.燕山大学 工程训练中心，河北 秦皇岛 066004；4.北京卫星环境工程研究所，北京 100094）

1 引言

六维力传感器能够对六分量作用力进行精确测量，并联机构具有刚度大、结构稳定、承载能力高、无误差积累、精度高、逆解求解容易的优点，所以并联六维力传感器具有广泛的应用前景。近年来，在精密装配、航空机器人、宇宙空间站对接等领域发挥了巨大作用，但对于火箭发动机推力试验、风洞实验等重大任务或重型装备应用环境，需要传感器具备重载能力，限于安装空间影响，传感器小型化也是必然需求，为此，学者们进行了广泛研究［1～6］。对于六维力传感器，标定是工程测试中的一个重要环节，直接影响到其性能和精度。付立悦等［7］对六维力传感器静态标定系统进行了误差分析，分析了标定误差主要来源；赵浩等提出了一种标定振动转矩传感器的方法，并验证了标定方法的可行性［8］。重载传感器承载力大，普通标定方法及设备难以达到实验要求，而对于风洞天平校准及火箭发动机推力测试场合，需要对传感器进行标定研究，所以重载传感器及其标定研究具有重要意义及发展前景。

重载六维力传感器采用并联弹性体加工而成，创新加入承载分支，具有结构紧凑、对称性好、刚度高、力映射关系清晰等优点，但由于加工工艺、测量环境等因素的影响，在应用六维力传感器测量时，通常会出现维间耦合［9］现象，所以需采用适用于重载传感器的标定算法以提高传感器的精度。在解耦算法中静态解耦算法的应用范围较广，学者们对静态解耦算法进行了广泛研究。在基于求解矩阵广义逆的静态解耦算法的研究基础上，茅晨等提出了基于耦合误差建模的静态解耦算法［10］，证明了基于耦合误差建模静态解耦算法的有效性。张家敏等［11］在传统的BP神经网络的解耦算法的基础上添加了改进的粒子群算法，采用粒子群算法优化神经网络，并应用到了六维力传感器的解耦算法中。王有贵等［12］提出了一种基于神经网络的称重传感器蠕变误差自动补偿模型，给出了模型的训练算法，减小了称重误差。

结合六维力传感器及标定研究现状，面向重载应用场合，研制了一种重载并联六维力传感器，为改善维间耦合等影响，对其进行了静态标定实验及标定算法的分析研究。

2 重载并联六维力传感器结构特点及测量原理

基于轮辐式并联六维力传感器［13］，融合小型化重载要求，通过仿真分析，创新加入4个承载分支，优选出了重载并联六维力传感器基本构型，结构示意模型，如图1所示。

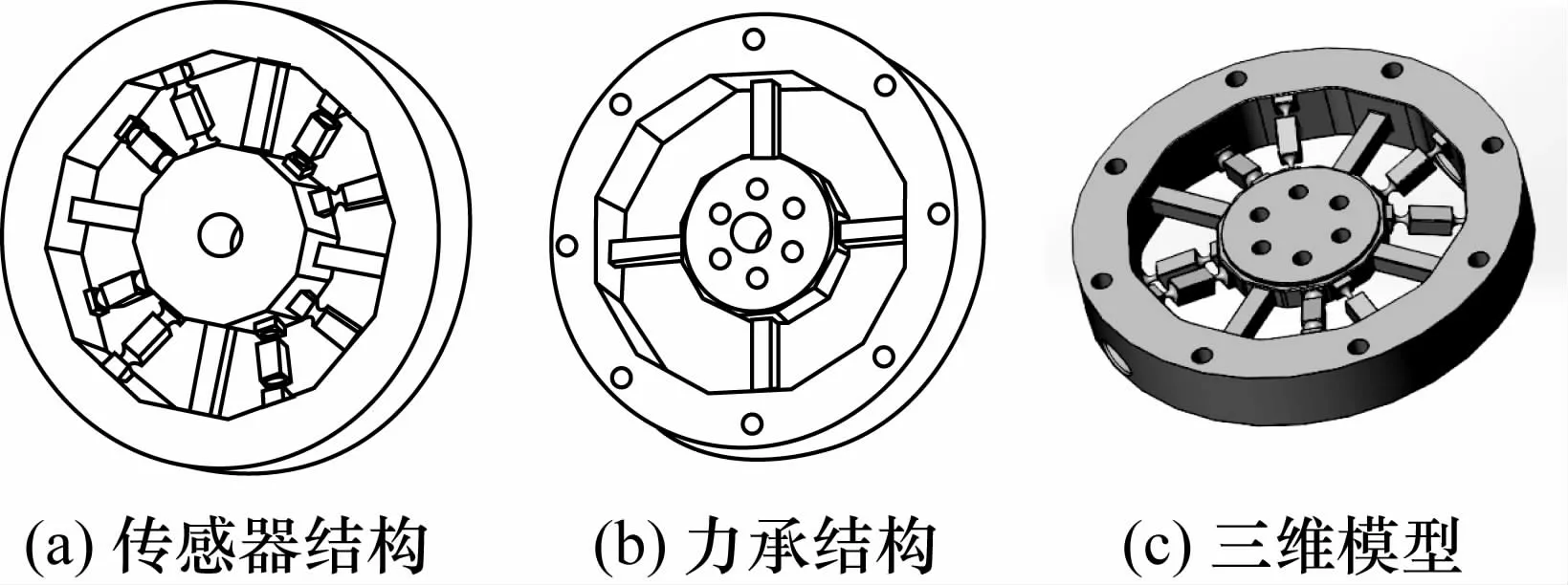
图1 传感器结构示意模型图Fig.1 The structural schematic model of the sensor

重载并联六维力传感器具有轮辐式冗余并联结构，实物如图2所示。传感器以内环为测量平台，外环为固定平台，8个测量分支通过内球铰和外球铰来联接内外两环。

图2 六维力传感器样机Fig.2 The prototype of parallel six-axis force sensor

重载六维力传感器构型与普通重载传感器构型相比：3个方向上受力更加均匀，结构紧凑，灵敏度更高，其中，8个测量分支用以监测分支受力变化，通过建立分支与测力平台的映射关系，进而能够准确测量出受力平台所受外力，承载分支则具有增大传感器刚度的优势，弥补了普通轮辐式传感器承载能力不足的缺点。

重载并联六维力传感器弹性体由钛合金粉末采用3D打印一体化成型技术加工而成，总体尺寸为ϕ180×H17，量程见表1。

表1 传感器样机量程Tab.1 The measuring range of the sensor prototype

传感器受力平台受到外力／力矩作用时，由空间力系静力平衡和映射关系可知，8个测量分支及4个承载梁会有相应力产生，测力分支通过应变片感知应变产生电压信号，经放大传输A／D转换至上位机，通过外力和分支电压信号的映射关系可求解传感器所受力／力矩，从而实现六维力的测量。

3 重载并联六维力传感器标定算法及误差评价

重载并联六维力传感器兼具冗余分支和承载分支，标定过程需考虑分支影响，综合考虑加工等误差影响，从传感器为线性系统和非线性系统2个方面来进行标定，采用最小二乘法和神经网络标定2种方法。

3.1 最小二乘法

传感器标定即求解六维外力与输出信号之间的映射关系，根据传感器设计原理及力平衡方程，可得六维外力与分支电压信号间的关系为

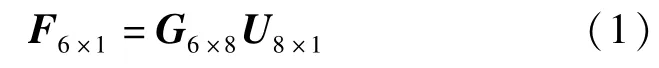
式中：F6×1为加载到传感器受力平台上的六维外力；G6×8为六维外力与电压信号间的映射矩阵，U8×1为分支在加载力作用下输出的电压信号。

因电压矩阵U为非方阵，其逆不唯一，根据矩阵理论，对式（1）中标定矩阵求解时，取最小范数的最小二乘解，求取U的最优逆矩阵解，则有：

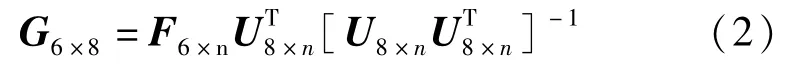
通过标定实验得到加载力与对应的电压信号，数据处理后即可得到传感器输入与输出间的映射关系。

3.2 BP神经网络标定法

考虑重载并联六维力传感器机械工艺及其它影响，传感器实则为非线性系统，采用非线性BP神经网络标定方法来对其进行标定，步骤如下：

1）生成网络。以六维力传感器8个分支的电压信号作为网络的输入向量，标定实验时加载外力作为网络的期望输出向量，则网络的输入层的节点数为8，输出层的节点数为6。输出层的传递函数为purelin（），隐层的传递函数选择tansig（），网络的训练函数为默认的trainlm。

2）权值、阈值初始化。对网络进行训练前，需初始化网络的权值和阈值，本次应用的是网络自动生成的权值和阈值。

3）训练网络。得到初始网络后，网络训练完毕，根据BP神经网络得到对应输入的电压信号即可计算得出加载力，进而得到对应不同隐层节点个数网络的非线性误差矩阵，通过比较各个非线性误差矩阵主对角线上的平均非线性误差确定隐层节点数。BP神经网络结构如图3所示。其中，h为隐层的节点数分别是隐层与输出层的权值，b1和b2分别是隐层和输出层的阈值。

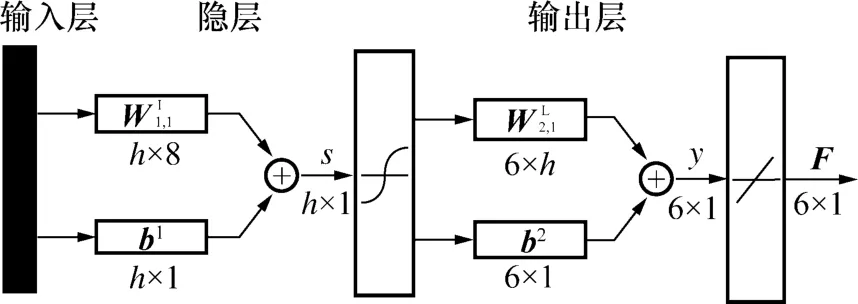
图3 BP神经网络结构图Fig.3 The structure diagram of the BP neural network

3.3 基于人工鱼群的BP神经网络标定

BP神经网络的算法具有计算过程简单、概念清晰的特点，但同时具有容易陷入局部极值的缺点，为了解决此问题，采用人工鱼群算法对BP神经网络进行优化。以下为人工鱼群算法对BP神经网络进行优化的过程：

1）选取合适的参数，包括鱼群中人工鱼的数量N、视步系数α、尝试次数以及迭代次数。

2）根据构建的BP神经网络结构，可得到网络中的连接权值与阈值的个数，将这些权值与阈值组成一个数组。在BP神经网络中输入层与隐层的连接权值矩阵为h×8的矩阵，其元素个数为8h个，隐层阈值矩阵为h×1的矩阵，其元素个数为h个，隐层与输出层的连接权值矩阵为6×h的矩阵，其元素个数为6h个，阈值矩阵为6×1的矩阵，其元素个数为6个，因此权值与阈值组成的数组中元素的个数为15h＋6。根据人工鱼的数量生成N组向量，其中每个向量表示每条人工鱼的位置状态，包含元素个数为15h＋6，且元素的赋值为0到1之间的随机数。

3）比较初始随机赋值的人工鱼群中各人工鱼所处位置状态的食物浓度，并选择最优值作为公告牌上的初始值。

4）设定初始迭代次数为0，进入人工鱼群算法的迭代过程，在鱼群中的每条人工鱼包含的元素个数相同，均为BP神经网络中权值与阈值的总数，且均被赋予随机数。设人工鱼的状态向量为A，那么2条人工鱼Ap与Aq之间的距离dpq为：

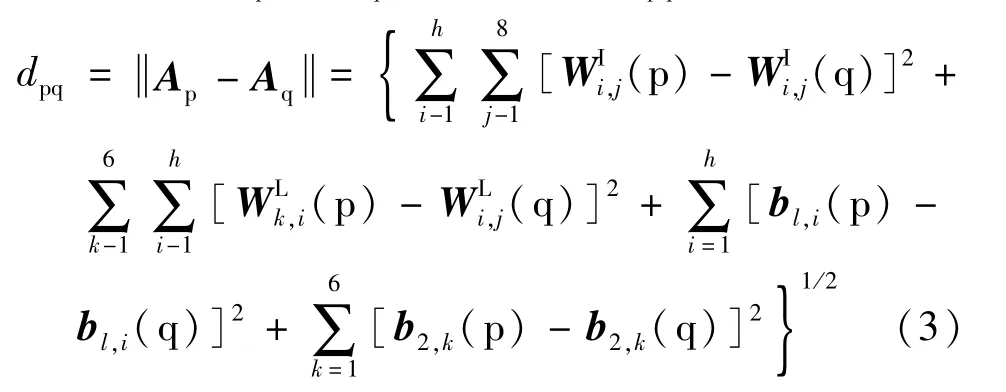
根据人工鱼执行聚群行为、追尾行为以及觅食行为时的视野范围和移动步长，每条人工鱼首先模拟聚群行为以及追尾行为，然后选择模拟后获取的食物浓度大的行为作为所要执行的行为，另外觅食行为作为缺省行为。

5）每条人工鱼在执行完行为后，对自身所处位置状态对应的食物浓度与公告牌上记录的值进行比较，若优于公告牌上记录食物浓度的值，就用自身所处位置状态对应食物浓度值替代公告牌上的值。

6）达到人工鱼群算法终止条件，得到最优的人工鱼的状态向量，提取该向量中元素作为BP神经网络训练时连接权值与阈值的初始值，进而再对BP神经网络进行训练。

3.4 误差评价

六维力传感器精度不同于单维力传感器，除了在作用力方向和该方向输出之间有输入／输出关系外，还存在维间耦合关系，传感器标定误差矩阵可作为传感器精度和耦合度的综合度量。

标定误差矩阵计算：将施加标准的6×6标定力矩阵和通过标定数据计算得到的施加力矩阵之差与传感器各维力／力矩满量程的比值定义为标定误差矩阵，标定误差矩阵ξ的表达方式如下：

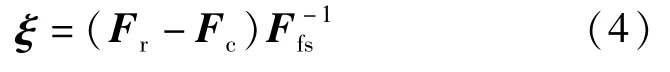
式中：Fr为实际施加的力矩阵；Fc为标定数据通过理论计算得到的力矩阵；Ffs＝diag［Fxfs，Fyfs，Fzfs，Mxfs，Myfs，Mzfs］为传感器各维满量程力／力矩值组成的6×6的对角阵。

传感器单维精度可通过Ⅰ类误差来表征，即标定误差矩阵对角线元素来反映测量值与实际施加值间的偏离程度，维间耦合程度则可通过Ⅱ类误差来表征，即其它非对角元素来反映不同维间的耦合程度。

4 标定实验结果

重载并联六维力传感器标定实验标定系统主要由硬件与软件2部分组成，如图4所示。硬件系统包括信号采集箱、上位机、砝码、千斤顶、六维力测量台，软件系统主要为LabVIEW 标定软件。

图4 六维力传感器标定系统Fig.4 The calibration system of six-axis force sensor

4.1 标定系统硬件

标定系统加载装置如图5所示，上方托盘用于放置加载砝码，与托盘连接的加载梁一端与传感器的受力平台固定连接，另一端与托盘中心连接，其中，加载梁两端的连接中心距离为10 cm，即加载力矩时的力臂为10 cm，传感器通过底座固定于六维力测量台中心位置，其底部分布有7个传感器，可得到平台中心所受到的六维力信息，六维力测量台的力值准确度为0.5%，扭矩准确度为1%，其量程如表2所示。标定信号采集箱如图6所示，其主要作用是对传感器输出信号进行放大、滤波和采集等工作。

图5 加载装置Fig.5 The loading device

图6 数据采集箱Fig.6 The data acquisition box

表2 六维力测量台量程Tab.2 The measuring range of force measuring table

重载并联六维力传感器的信号采集程序由LabVIEW 编制，经采集箱处理过的数据传输到计算机，通过此程序来记录数据。

4.2 标定过程

重载并联六维力传感器加载时将加载区间分成若干个加载点，具体标定过程如下：

1）确定传感器各维力正方向，采集系统预热；

2）加载Fx时采用千斤顶进行满量程加载，从Fx正方向开始标定，记录加载点电压信号和六维力测量台测得的加载力，卸载后进行Fx负方向加载，步骤同Fx正方向；Fy方向的标定加载过程与Fx相同；

3）加载Fz方向时，采用砝码加载机进行加载，从零点加载到满量程3 kN，并记录各加载点的电压信号与加载力；

4）加载Mx方向力矩，在托盘上放置砝码，Fz方向的力与加载梁力臂乘积所产生的力矩即为所求。加载砝码每个重50 N，从零点开始加载到满量程50 N·m，记录每个加载点信息，卸载后再进行反方向加载；My方向标定加载过程与Mx相同；

5）加载Mz方向力矩时，通过Fx方向的力与力臂的乘积产生Mz方向力矩，Fx方向的力由千斤顶加载，通过六维力测量台记录加载到传感器上力和力矩的大小。从零点开始加载到满量程90 N·m，记录每个加载点的信号与六维力测量台测得的力和力矩信息，卸载后反方向加载，步骤同正方向；

6）完成上述工作后，保存加载力与信号数据。

4.3 实验结果分析比较

4.3.1 最小二乘法结果

对标定后的数据进行最小二乘法处理，即将处理后的标定数据代入式（2）进行求解，得到标定矩阵为：

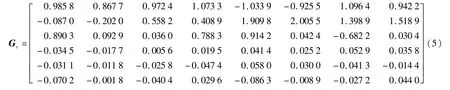
利用求得标定矩阵Gc，计算相对应的施加力，进而可得标定误差矩阵为：

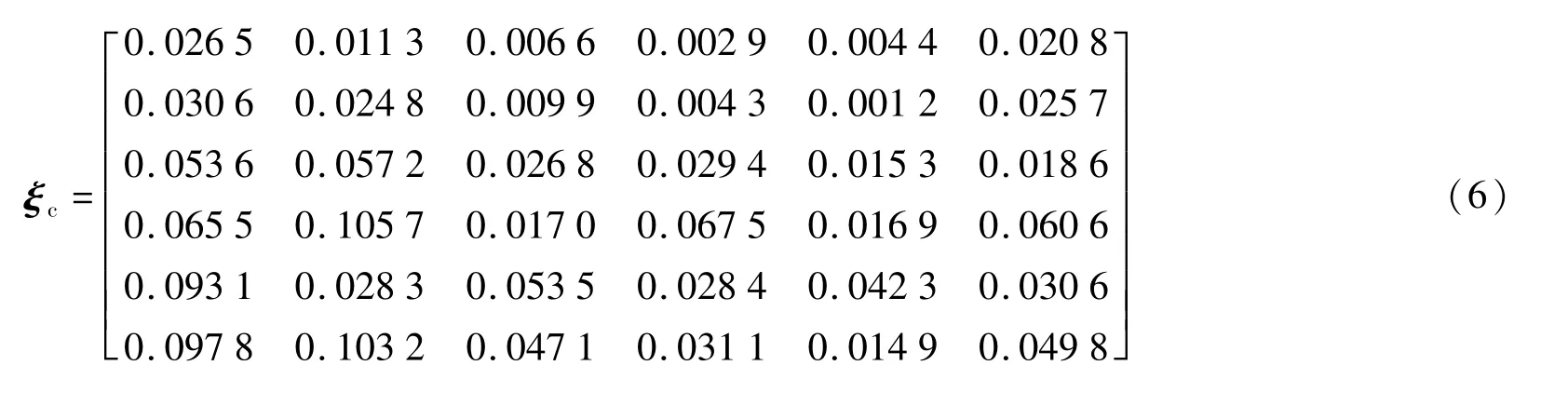
由式（6）可知，主方向上最大非线性误差为6.75%，最大耦合误差为10.57%。分析原因为加载力矩时非纯扭矩，导致计算结果中力与力矩会有一定的耦合，此外，在标定误差矩阵中，加载力矩时力矩方向上的非线性误差会有加载力的耦合作用；因此在力矩主方向上的非线性误差中也会含有耦合误差，同样加载力矩时对应加载力的误差也会有加载力矩的耦合作用。

4.3.2 BP神经网络

通过对比根据不同隐层节点数的BP神经网络所得到的非线性误差矩阵，可知隐层节点数为14个时的效果最好，对应的标定误差矩阵为：

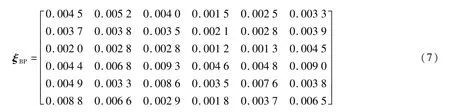
由式（7）可知，当隐层节点个数为14个时得到的非线性误差矩阵中主方向上最大的非线性误差为0.76%，最大耦合误差为0.93%。相比于最小二乘法标定算法得到的结果，采用BP神经网络的标定算法的效果具有明显的优势；但因在初始化神经网络时为随机的方式，由此造成每次对应的网络不同，每次训练结果不同，即隐层的节点的最优个数不一定是14，并且即使是相同隐层节点每次的训练结果也会有所不同。

4.3.3 算法分析验证

BP神经网络和最小二乘法2种标定算法在计算中，输入输出关系的求解与验证采用的是同一组数据，为了能准确体现计算得到传感器映射关系的准确性，将静态标定实验的得到的数据分成2部分，一部分用于标定计算求解输入输出之间的关系，另一部分用于求解非线性误差，以此来验证结果的准确性。

首先采用Matlab编写程序，对静态标定的数据进行分组，采用交叉间隔选取的分组形式进行分组，最后结果是得到82组用于标定计算的数据与41组用于测试的数据，然后再用这些数据进行分析计算。

将用于求解标定矩阵的82组标定数据代入式（2）求解标定矩阵，结果为：

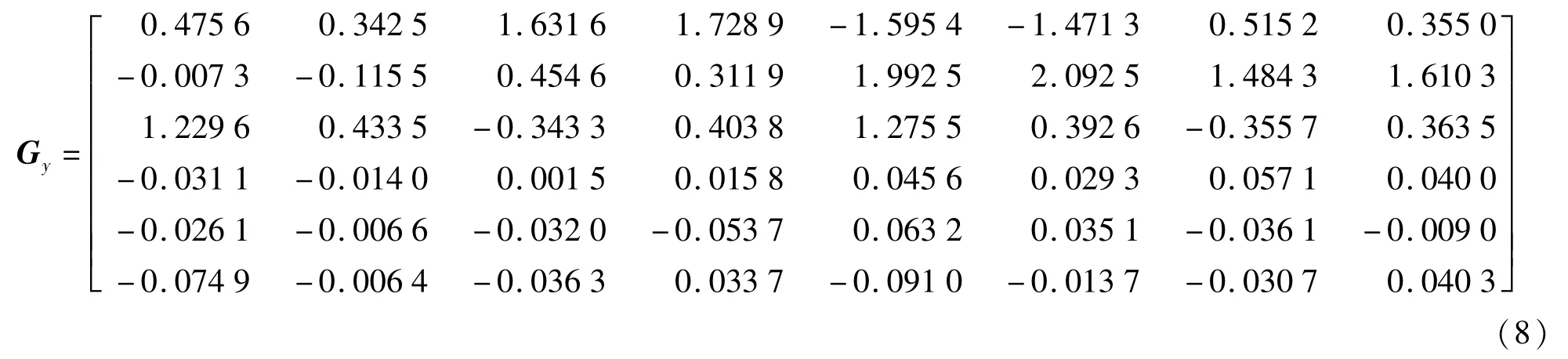
求得标定矩阵后，根据用于测试的41组电压信号的数据与标定矩阵求解加载力，进而得到对应的标定误差矩阵为：

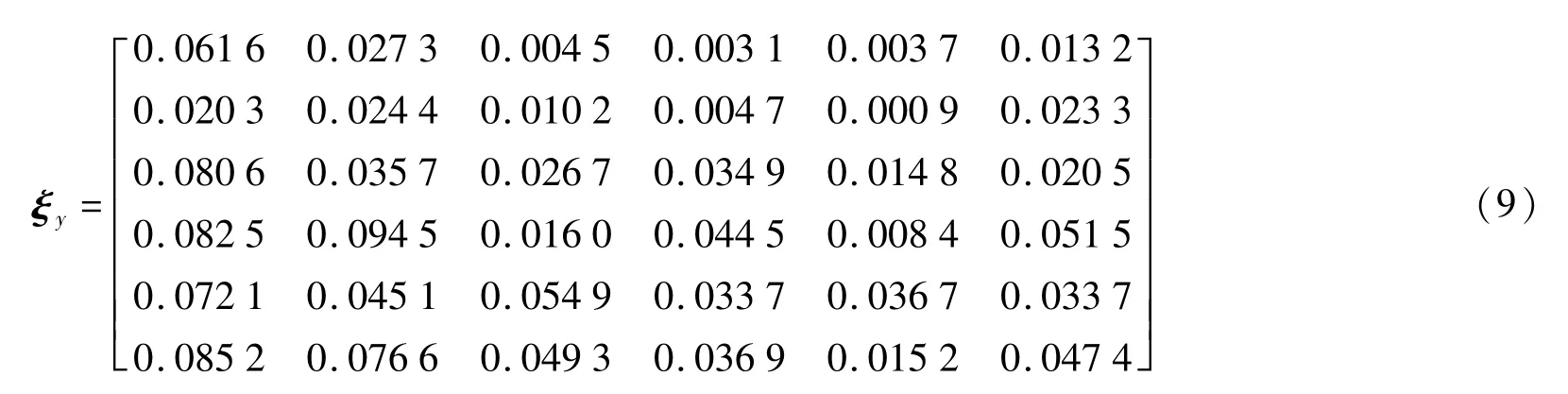
由非线性误差矩阵可以发现，当采用最小二乘法标定算法，应用由标定计算的数据得到的标定矩阵来计算测试用数据的非线性误差时，得到主方向的最大线性误差为6.16%，最大耦合误差为9.45%，与采用同一组数据的计算结果相近，即采用最小二乘法的标定算法与标定结果具有一致性。

将用于求解传感器输入输出之间对应关系的82组标定数据放入神经网络中进行训练，然后将41组用于测试的数据代入训练完成的网络，根据网络输出的加载力和41组测试中的加载力以计算非线性误差矩阵，通过对比不同隐层节点个数神经网络的结果得到当隐层节点个数为10时结果最好，其对应标定误差矩阵为：

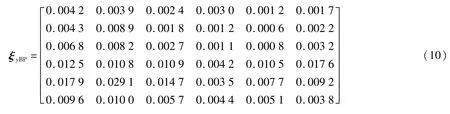
当BP神经网络的隐层节点个数为10个时，由测试数据得到的标定误差矩阵主方向上的最大线性误差为0.89%，最大耦合误差为2.91%。所以BP神经网络的标定算法同样也具备准确性，且针对本系统其效果明显优于最小二乘法。

4.3.4 BP神经网络算法优化

为了验证人工鱼群算法程序的可行性与有效性，以BP神经网络隐层神经元个数为14时为例，通过人工鱼群算法对其进行优化，选取人工鱼群算法的参数时，人工鱼的数量选为140个，视步系数为0.5，尝试次数选为2次，迭代次数选为100，通过运行程序得到最优人工鱼的状态，并将提取的权值和阈值代入BP神经网络中，经过优化的BP神经网络作为标定算法时得到的标定误差矩阵为：

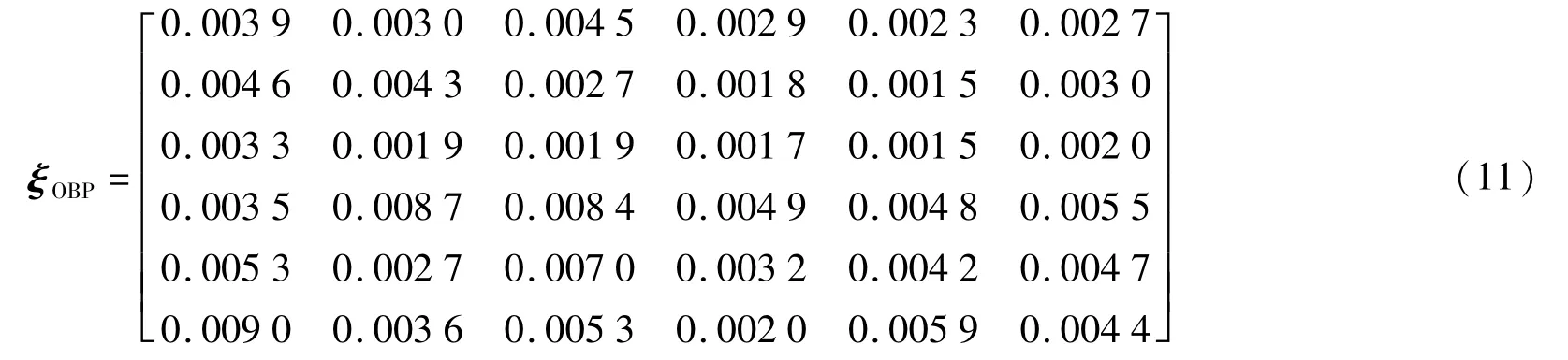
根据式（11）可知，其非线性误差为0.49%，最大耦合误差为0.9%。应用BP神经网络直接进行训练得到的标定误差矩阵为：

根据式（12）可知，其标定误差矩阵主方向上的非线性误差为0.61%，最大耦合误差为1.75%，不同标定方法得到传感器各维力精度如表3所示。

表3 不同方法传感器精度Tab.3 The sensor accuracy of different methods（%）

通过比较分析，经人工鱼群算法优化的BP神经网络计算结果要优于BP神经网络，且通过多次运行程序发现，经过人工鱼群算法优化的BP神经网络所得到的结果较稳定，且不易陷入局部极值；因此，经人工鱼群算法优化后BP神经网络标定算法的效果更好。

5 结论

（1）研制了一种具有混合分支的重载并联六维力传感器，分析说明了传感器的结构特点，其中，8个测量分支用以监测分支受力变化，增加的4个矩形梁结构承载分支具有增大传感器刚度优势，弥补了普通轮辐式传感器承载能力不足的缺点。

（2）进行了重载六维力传感器静态标定实验研究，将标定实验数据，根据不同情况在传感器为线性与非线性系统的情况下，采用不同标定算法分别对其进行了标定计算，实验结果表明传感器各维力／力矩分量测量精度良好，通过不同算法间的分析比较，得到了利于传感器标定的不同思路，并通过数据的随机分组测试分析验证了标定算法的准确性。

（3）基于BP神经网络标定分析结果，优化提出了基于人工鱼群算法的BP神经网络的标定算法，优化后每次训练较为稳定，不易陷入局部极值，结果较好并具有一定的优越性。

本文的研究为重载六维力传感器的研究及标定和应用提供了一定的参考。