双同步电机系统轴系柔性有限元建模及扭振特性分析

吴 刚 高 丰 梁 超

(①兖煤菏泽能化有限公司赵楼煤矿，山东 菏泽 274705；②天津德通电气股份有限公司，天津 300380)

同步电机是深井提升系统中关键的动力设备，随着矿井深度的不断加深，为保证对深井的正常开采，如今多数深井提升系统采用双同步电机对滚筒进行同时拖动，低频运行状态下会增加扭振发生的风险，从而导致发生主轴断裂事故[1-2]。双同步电机系统的轴系在运动过程更会存在形变与振动，精确建模不仅对轴系扭振特性的分析和对运行时轴系故障受损影响有着重要作用，而且轴系结构的设计等也具有重要现实意义[3-5]。

轴系扭振动力学分析理论发展较为成熟，多采用集中模型和连续质量模型法[6-8]，周生通[9]为有效地模拟传动轴系的扭转振动特性建立了集总参数模型，陈星等人[10]对同步电机转子系统建立双质量模型，证明了转子系统扭振的稳定性并确定了它的稳态解。付强等人[11]在考虑阻尼作用下用整体传递矩阵法计算转子的固有特性。Zhu Z Q等人[12]在对同步电机轴系的扭振特性分析时采用连续质量法和相应的传递矩阵法，得出的结果与实际测试值几乎相同。但集中质量和连续质量模型忽略了轴系关键部件的阻尼和刚性，不能准确反映对轴系的动态扭振特性。针对这种情况，HELSEN J和何玉林等人[13-14]对结构使用了建立柔体模型的方法来分析其特性，证明了柔性建模是对扭振特性分析具有重要相应作用的。同时有限元建模可以精确地反映同步电机系统轴系的复杂时变扭转振动特性，而不受参数设置的限制。黄晓刚等[15]使用有限元法对轴系的扭转振动固有频率进行了计算，为用有限元方法分析轴系的扭振提供了依据。王超，庞乐等人[16-17]采用了有限元法对扭振特性进行分析，证明了其方法可以进一步提升轴系的固有频率计算的精准度，但把轴系考虑为刚性体，且未考虑联轴器柔性。

双同步电机的结构单比电机更加复杂，不仅轴系更长而且连接点也更多，在运行中是一个多自由度多柔体的耦合系统，所以单自由度纯扭转动力学模型全刚体动力学模型不能真实表达双电机轴系的动态特性。因此本文提出对双同步电机系统轴系进行柔性的有限元建模的方法来分析其扭振特性。首先根据同步电机实际参数建立双电机系统轴系的柔性有限元模型，并通过有限元法对其进行扭振特性分析对比验证了对轴系进行柔性建模这种方法的高效性，最后分析柔性参数变化对系统轴系扭振特性的影响。

1 双同步电机系统轴系建模

1.1 柔性建模

与刚性体建模相比，柔性体建模对运动特性和动力学表达的更为清晰，也提升了结构仿真中特性分析的可靠性和精准度[18]。它的基本思想就是将模态向量和模态坐标表示结构体的弹性模量，具体就是将整体结构离散化为有限元柔性模型来表示结构的无限自由度。

如果在惯性坐标系下的笛卡尔坐标用η=(x,y,z)T表示；用γ=(φ,θ,ψ)T来反应刚体方位的欧拉角，模态坐标用q={q1,q2,...,qs}n(n为模态坐标数)来表示的话[19]，则可以表示柔性体的广义坐标ξ向量坐标为：

(1)

广义坐标下的柔性体运动微分方程如式(2)

(2)

式中：M表示结构的质量矩阵；K表示广义坐标系中的刚度矩阵；D表示模态阻尼矩阵；φ代表柔性体的约束方程；fg代表广义坐标中的重力；λ代表拉格朗日因子；Q代表广义坐标下的作用力[20]。

1.2 柔性有限元建模实现

双同步电机系统轴系主要由电机主轴、电机转子、联轴器、滚筒轴系等部件组成。本文以某矿井7 800 kW同步电机为例，其实际尺寸参数如表1所示。利用Auto Flex模块柔性化处理两个联轴器及两根传动轴，先通过Geometry来创建刚性体文件，然后把从Solid Tetra四面体单元中创建的模态中性文件替换刚性体，在SolidWorks平台将双同步电机系统轴系实体部件进行装配如图1所示，在装配时考虑到传动轴和联轴器直接的机械耦合因素，对连接部位的摩擦因数进行设置，通过调节各连接部位的摩擦因数设置为0.2，使其在减少机械阻尼的同时也能准确地模拟实际轴系运行情况。

最后将在SolidWorks中生成的文件导入ANSYS中建立双同步电机系统轴系柔性有限元模型并对其进行仿真。其中使用Solid45单元模拟主轴，并对轴系两端的电机尾端的轴承支点进行固定，划分网格模式选取非线性结构模式，网格划分采用六面体主导的网格划分，所建立的柔性有限元模型如图2所示。

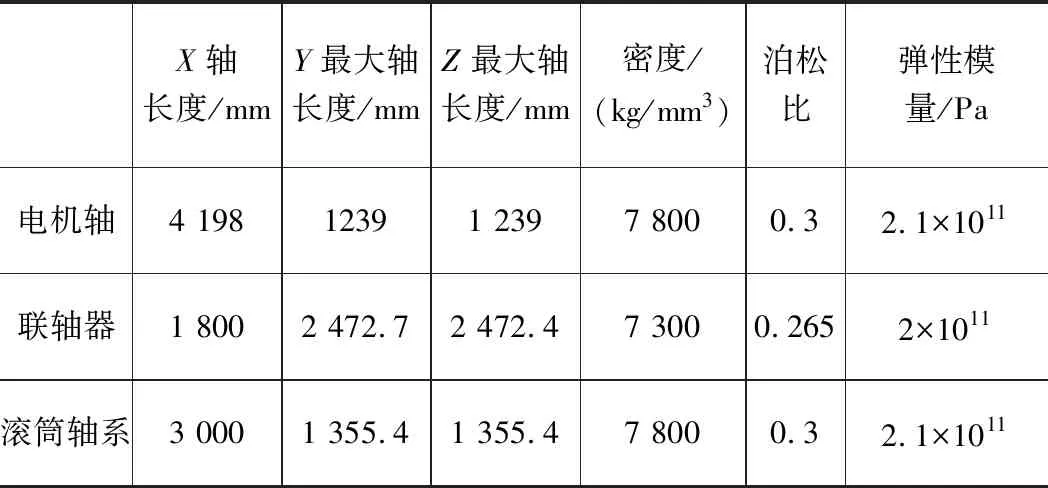
表1 同步电机实际参数

2 基于有限元法的扭振特性分析

2.1 双同步电机系统轴系模型模态分析

模态分析主要是对结构的固有频率及振动振型及振动位移等振动特性进行研究。实质上就是求解在没有阻尼和外界载荷情况中多个自由度运动方程的模态矢量，通过分析可以了解某个频率范围内轴系的主要振动特性，并对种种振动源影响下的实际振动响应进行预测。因此结构的无阻尼自由振动方程的矩阵表达式为[21]：

(3)

式中：[M]表示系统质量矩阵；[K]表示轴系的刚度矩阵；u表示位移向量。

通常设式(3)的解为：

x={φ}sin(ωt+θ)

(4)

式中：{φ}表示振幅列阵；ω表示角频率；θ表示初相位。

将式(4)代入式(3)得

(K-ω2M){φ}={0}

(5)

为求得式(5)的非零解条件是其系数行列式的值为0，即

|K-ω2|=0

(6)

将特征矩阵展开得到关于固有频率ω2的n次代数方程。求出这个方程的n个根，从而得到n个固有频率ωi=(i=1,2,...,n)。令{φ}与相应的ωi的主振型代入式(6)，

(7)

对该方程进行求解的主振型{φi}(1,2,3,...,n)。

由于整个轴系的固有频率分布数量多而且分布较近，因此本文对模态分析的结果采用了矢量位移云图的方法对固有频率筛选出150 Hz以内的8个固有频率如表2所示，扭振振型图如图3所示。

由图3给出的振型图可以看出系统轴系发生扭振的部位主要是联轴器和转子，由于双同步电机的结构扭振发生的部位有着对称特性。其中1～4阶次的扭振主要发生在轴系联轴器两侧，频率为15.791 Hz的时，联轴器发生的相对扭振幅度最大，而5～8阶扭振主要发生在电机转子及两侧，在第6阶振型时转子发生的相对振幅变化最大，由此可见低频谐波对柔性的联轴器及其周围部件产生影响最大，而电机则受中高频频率影响。由振型图可以看出发生在联轴器和主轴两侧的低阶次扭振振幅变化很大，又因双电机联轴器连接处的扭转振动对轴系结构有影响最大，因此联轴器最容易进一步引发轴的断裂或者其他危害。

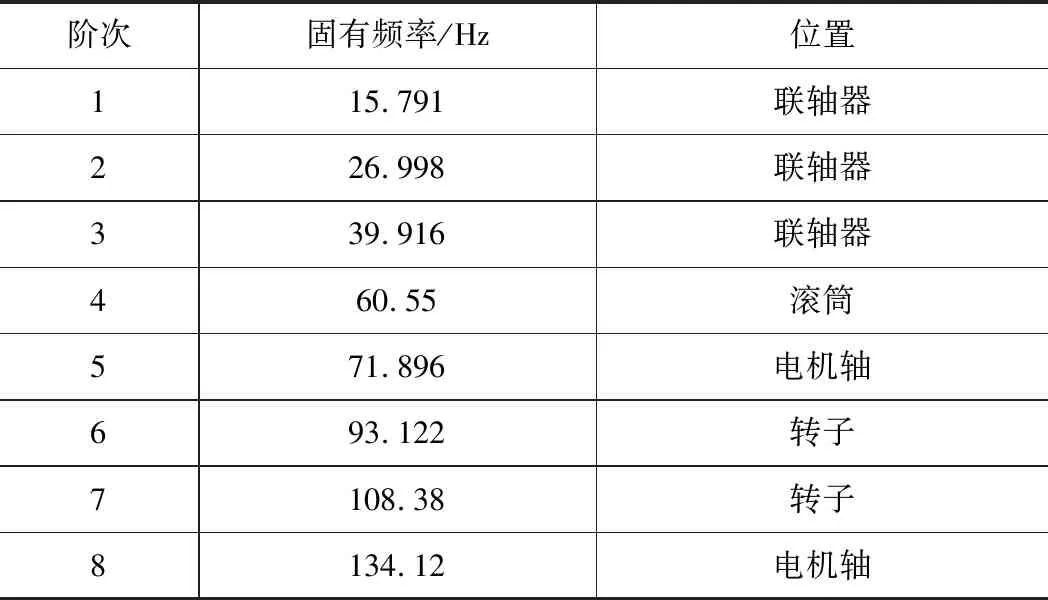
表2 双同步电机轴系固有频率

2.2 双同步电机轴系正弦响应分析

结合模态分析的分析结果可以看出在各阶模态振型中容易发生扭振的位置是两个联轴器和转子部位，对这两个位置施加不同频率的各种正弦载荷可以更清楚的看出联轴器和转子的响应状态。 因此对联轴器和转子部位施加200 N/mm的扭矩载荷，激振频率范围为0～150 Hz。得到联轴器和转子的幅频响应曲线分别如图4所示。

由图4a可知，联轴器部位在YZ方向上的振幅随着频率的变化在15 Hz、40 Hz和60 Hz会有峰值的出现，第一次的峰值振幅为0.67×10-5mm，然后迅速下降，后两个峰值振幅明显小于第一阶位移峰值。说明联轴器在低频时容易发生扭振。在图4b中，转子部位也是在YZ两个方向上随着频率的增长出现明显振幅波动，在频率为 95 Hz 左右时出现振幅峰值0.005 4×10-5mm，然后下降，随后在105 Hz处再次出现振幅但小于第一次，可以看出高频时容易发生扭振的部位是转子。

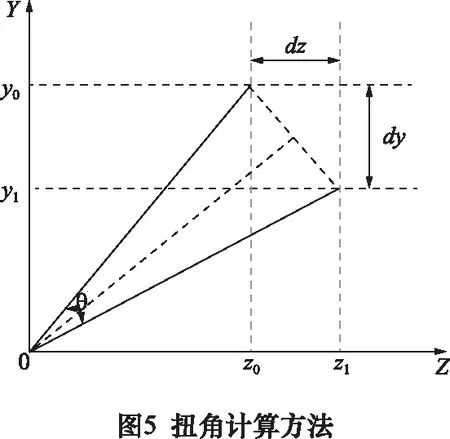
同时由图4可看出，联轴器和转子的X方向即轴向位移相对于YZ方向非常小，因此主要表现为扭转振动。为了更加直观表示联轴器和转子部位的扭转角度变化，对轴系任一点初始坐标为(x0,y0,z0)，施加载荷后坐标为(x1,y1,z1)，扭转角度为θ，则由图5扭角计算平面图可计算出θ。当扭角非常小时，可以近似认为该三角形为等腰三角形，则有：

(9)

由此可以得出扭角-频率变化曲线，如图6所示。结果与图4结论相似，联轴器在15 Hz出现最大扭角，约为0.78°，该一阶扭振对系统影响最大。而转子在95 Hz左右扭角最大，约为0.15°。此结论与表2的固有频率大体一致，有略微的偏差，原因可能为进行正弦响应分析的时候由于设置载荷子为30步，未涵盖固有频率点析，故分析的结果会存在偏差。当施加中低频载荷时，在表2所示固有频率点附近均激发其较大的扭转角度，说明了中低频振荡是引发联轴器部位发生扭振的重要原因，也更一步证明了本文分析方法的精准性。

2.3 不同建模方法比较

针对柔性体有限元建模方法的有效性分析，本文采用不同的建模方法与之对比，表3列出了3种方法的分析结果。其中，文献[22]的建模方法只提到了每个部件之间的扭转自由度，并且建立了由弹簧连接的纯扭转质量块的集中质量全刚性轴系模型；文献[23]的是建立的是只考虑了轴类部件柔性，忽略轴与负载连接处的柔性的建模；而本文模型则考虑各同步电机主轴和各个关键连接部位的整体柔性有限元模型。

>

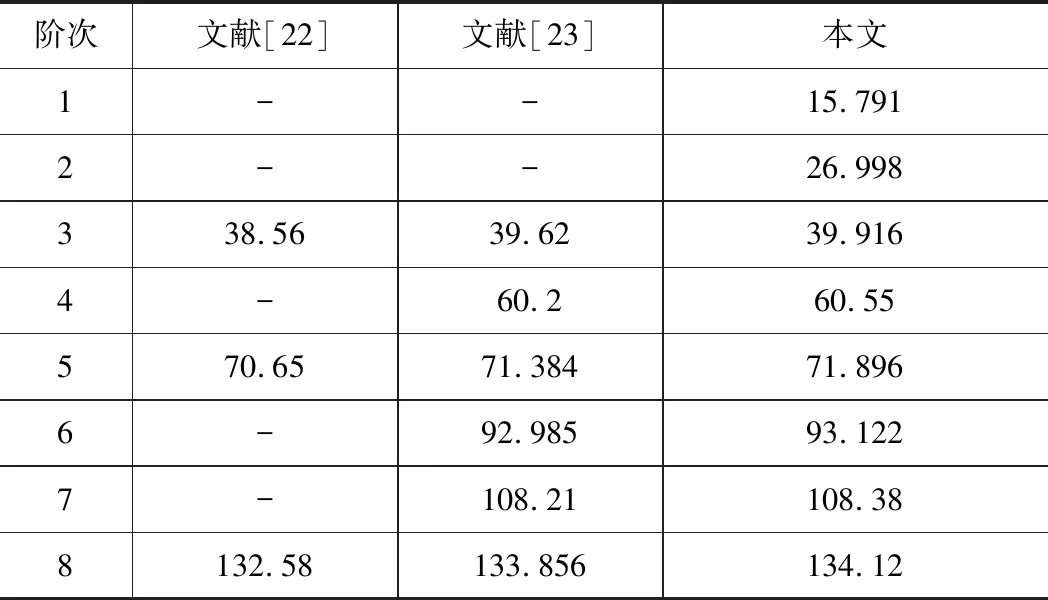
表3 3种模型扭转频率对比

从表3中可看出，文献[22]的集中质量模型不能完全表现出双同步电机轴系扭振特性的所有相关固有频率，尤其是在低频段的时候完全无法显示轴系的扭振特性。文献[23]的建模方法缺少了对关键连接部位联轴器的柔性化，使得低频时联轴器主要扭振频率和无法提取。

从结果可看出，双同步电机的关键连接部件柔性建模的重要性，如果建模时的柔化性不完全甚至全刚体性建模就会会导致在双同步电机轴系的扭振特性分析中的固有频率提取的不准确或无法计算出来，从而无法精准地对结构进行特性分析。

3 不同部位柔性对扭振特性分析的影响

3.1 联轴器柔性变化对轴系扭振特性的影响

为了加深进轴系关键连接部位联轴器柔性变化对轴系扭振特性的影响的研究，本文在所建立的柔性有限元模型的基础上将联轴器的弹性模量改变为正常值的50%和 200%，各阶模态和与其对应和扭振频率如图7所示。

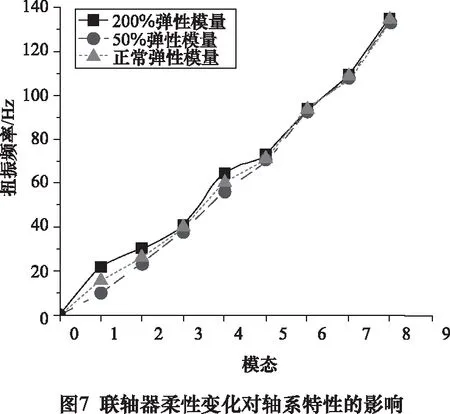
从图7可看出，联轴器柔性参数的改变对系统轴系的扭振特性表现有着一定的影响，尤其是低频率模态发生了较明显的变化。随着联轴器柔性的增加，扭振频率随之减小；当联轴器刚性增大时，也就是增大其弹性模量，扭振频率随之增加。与此同时，对高阶扭振模态的影响可以忽略不计，主要原因是由于在中低阶模态频率主要是由系统的连接设备联轴器及负载滚筒激发的，因此改变联轴器柔性对此部分扭振影响较大，对轴系的高频模态频率基本无影响。

3.2 同步电机主轴柔性对轴系扭振特性的影响

为了加深进同步电机主轴的柔性变化对轴系扭振特性的影响规律的研究，本文在所建立的柔性有限元模型的基础上将同步电机主轴之间的弹性模量改变为正常值的10%和1 000%，各阶模态和与其对应和扭振频率如图8所示。

从图8可看出，同步电机主轴的柔性的改变对系统整体的扭振特性的影响不是很大。由于电机主轴主要起的是一个进行机械传动的作用，因此改变电机主轴的柔性，主要对电机运行时的高频频率有着一定影响，随着柔性减小，扭振模态的固有频率频率随之上升；随着柔性增加，扭振模态的固有频率随之下降。同时，与联轴器柔性改变对整个轴系的影响相比较，同步电机主轴的柔性的改变对整个轴系的影响可以忽略。

4 结语

针对双同步电机在实时工况下运行会发生的扭振问题本文提出了一种轴系柔性有限元建模方法，并在有限元软件中进行模态分析主要结论如下：

(1)本文对双同步电机系统轴系进行柔性建模，不仅克服了集中质量模型的过度简化不能完全表示扭振特性的缺陷，也避免了连接部位刚性建模时导致的频率缺失。

(2)双同步电机系统轴系扭振频率15～140 Hz，主要扭振部位是联轴器和转子部位，振动位置以滚筒为中心呈对称特性。由响应分析可得出低频运行时联轴器部位扭振的风险增加，而高频运行时容易发生扭振的部位则是转子，同时也验证了本文方法的可行性、有效性。

(3)与电机主轴柔化相比联轴器柔性系数对双同步电机轴系特性影响较为明显，通过改变联轴器弹性模量可以看出联轴器刚性增加，扭振频率上升；联轴器柔性增加，扭振频率下降。