匕首刀超声切削Nomex蜂窝芯复合材料切削力预测模型构建

袁信满 曹文军 张 桂 王贵鑫 周 进 唐正明

(①成都飞机工业(集团)有限责任公司，四川 成都610092； ②西南石油大学机电工程学院，四川 成都610500)

相较于传统材料，Nomex蜂窝芯复合材料以其质轻、密度小以及刚性大等优秀的物理性能，成为船舶、航空和航天等领域不可或缺的高性价比材料[1-2]。传统切削加工中，蜂窝芯复合材料的多孔薄壁结构和特殊的各向异性力学性能使其在加工过程中出现诸多缺陷，存在蜂窝孔格变形、纤维拔出和刀具急剧磨损等问题，严重影响了产品构件的使用性能，可加工性差成为限制其应用的关键因素。

近年来，以“切割”为核心的超声切削加工技术被用于蜂窝芯复合材料的加工中，通过在刀具上施加超声振动，形成与传统切削不同的高频碰撞使刀具更有效的打开材料分子结构[3-4]，以实现切削力小、精度高及无污染的加工形式，克服了传统切削中存在的诸多问题。

切削力是评价产品二次加工过程的重要指标，国内外学者对Nomex蜂窝芯切削过程中的切削力进行了大量的研究。Levent Aktaya[5-6]等人从微观力学的角度出发，针对蜂窝芯复合材料横向刚度低的特点，建立了其横向挤压仿真模型，为后续的蜂窝芯复合材料的力学研究奠定了基础。徐龙[7]等通过分析蜂窝芯切削过程中的压溃过程及破坏机理，针对性地提出非常规的逆向加工薄壁蜂窝型面的方法，能有效地改善传统方法中蜂窝薄边易脱胶的问题。Karakos A[8]等人通过实验测得了蜂窝芯材料拉的应力应变关系，为蜂窝芯复合材料的切削模型建立奠定了理论基础。张生芳[9]通过建立圆盘刀超声切削蜂窝芯的有限元模型，分析刀具切削参数对切削温度的影响，当刀具后角增加时，刀具受到的摩擦阻力减小，切削温度降低，产品表面质量提高。方亮[10]针对圆盘刀的刀具结构，通过建立铣削蜂窝芯的应力场数学模型，研究刀具在切削力作用下的变形情况与应力分布规律，完成了圆盘刀的结构优化设计，在这种圆盘刀的蜂窝芯超声铣削中，加工后的蜂窝材料表面光滑无毛刺。

马付建[11]将蜂窝芯的传统切削与超声切削对比，超声加工有突出的加工优势，能极大的降低切削力。黄秀秀[12]针对直刃刀具分析蜂窝芯材料超声振动切削时的运动特性，结合遗传算法的优化设计，获得了极佳的切削加工参数，提出合理的刀具摆角、刀具前倾角能有效降低切割力的影响，极大地提高产品质量。王毅丹[13-14]在此基础上从脆性力学的角度出发，分析蜂窝芯与刀具的相对运动关系，得出材料在不同振幅情况下，破坏呈连续和断续2种形式，并以实验证明降低进给方向的刀具振幅能有效降低切削力。Ahmad S[15]等通过一系列单因素和四因素四水平正交试验，研究了超声波圆锯片(UCSB)和超声波圆刀(UCK)刀具的加工参数对旋转超声加工(RUM)切削力和表面质量的影响。袁信满[16]针对真空吸附夹持的蜂窝芯材料，建立匕首刀切削力理论模型，通过仿真与实验对比分析验证了模型的有效性，利用遗传算法对切削参数进行优化，改善了加工质量。Jiang J[17]等提出了一个切削力模型预测不同刀具入口角度下的铣削力，对蜂窝壁的加工进行有限元模拟，揭示撕裂缺陷的形成机理。

目前关于Nomex蜂窝芯切削的研究大多集中于加工参数对加工质量的影响和刀具结构的优化上，加工参数对切削力影响规律方面的研究甚少，缺少切削力预测模型。为进一步改善蜂窝芯复合材料加工质量，本文以不同切削深度、进给速度、刀具前倾角和刀具侧倾角设计匕首刀蜂窝芯超声切削加工实验，以考察不同切削参数对切削力的影响规律，从而建立切削力预测模型。

1 匕首刀超声切削蜂窝芯试验特征及分析

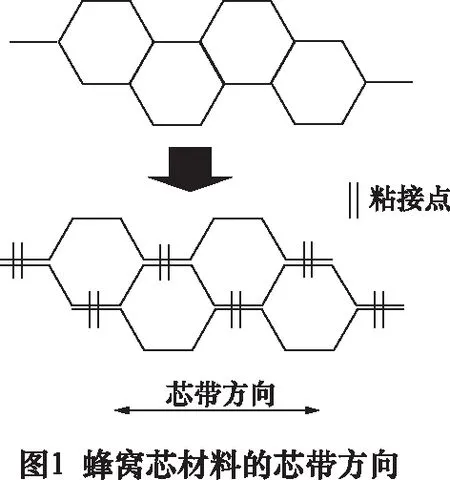
匕首刀超声振动切削蜂窝芯零件的过程中，匕首刀相对于零件的运动由两个分运动组成：一个是刀具沿其切削轨迹的进给运动，一个是刀具沿其轴向的超声振动[15]。切削力作为反映切削基本特征的重要参数，往往与切削深度ap、进给速度vf、刀具前倾角α及刀具侧倾角β存在一定非线性关系。并且在大量的实验基础上发现，切削方向与芯格方向的一致性也在一定程度上影响匕首刀切削力。蜂窝芯复合材料的成型过程中存在如图1所示的两种粘接方式，当切削方向与芯带方向不一致时，切削力也会不同，原因在于蜂窝芯复合材料制造过程中的粘接方式会在一定程度上影响切削力。

蜂窝芯为非均质(连续)材料，仅当刀具切削到芯格壁时才产生切削力，连续采集切削力时，以前倾方式切削的匕首刀会同时与多个蜂窝芯芯格产生接触，某一时刻采集到的切削力为各芯格所受切削力的合力。

因此，刀具切削时同时接触的芯格壁个数会影响平均切削力的大小。如图3所示，在不同的切削位置下，单位距离内的芯格壁数量不同，导致切削过程中匕首刀与芯格壁接触数量不同。因此在实验过程中，需考虑切削位置对切削力的影响。

2 实验方案

2.1 实验设计

实验采用中心复合响应曲面法，以切削深度ap、进给速度vf、刀具前倾角α，刀具侧倾角β为自变量，x向、y向、z向的切削力为响应值。中心复合设计及响应曲面参数如表1～2所示。

表1 响应曲面水平设计

2.2 实验装置与条件

匕首刀超声切削蜂窝芯实验在RMT-50机床上进行，超声振动频率为20 kHz，无冷却液切削，实验材料为某无人机所用蜂窝芯复合材料，相关信息见表3。

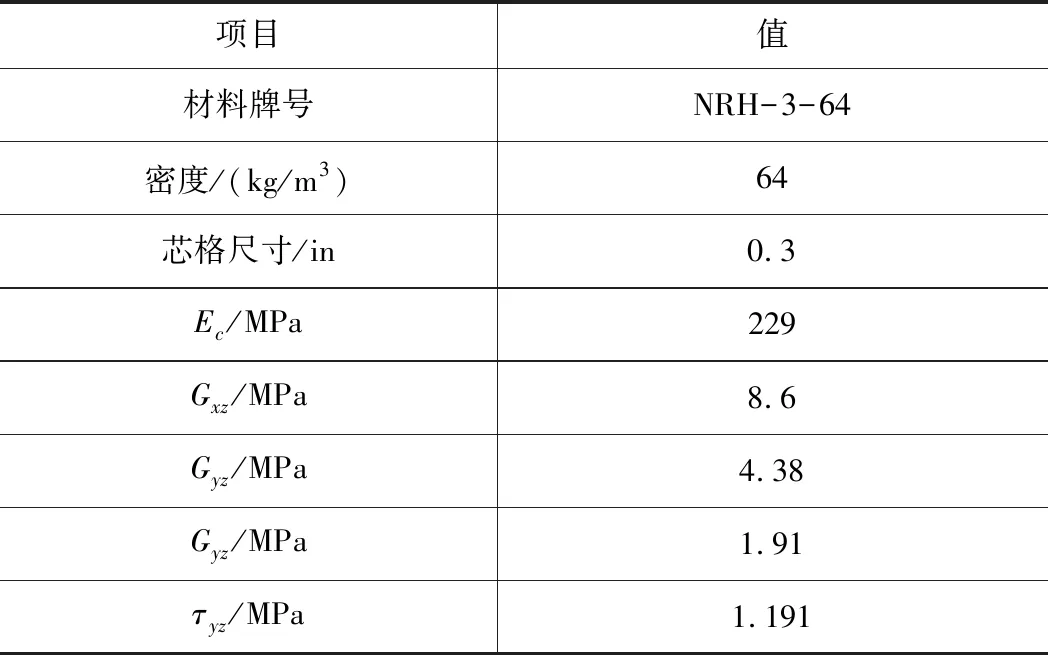
表3 蜂窝芯试验件材料信息

实验所用刀具为双刃匕首刀具，刀具结构信息见图4。

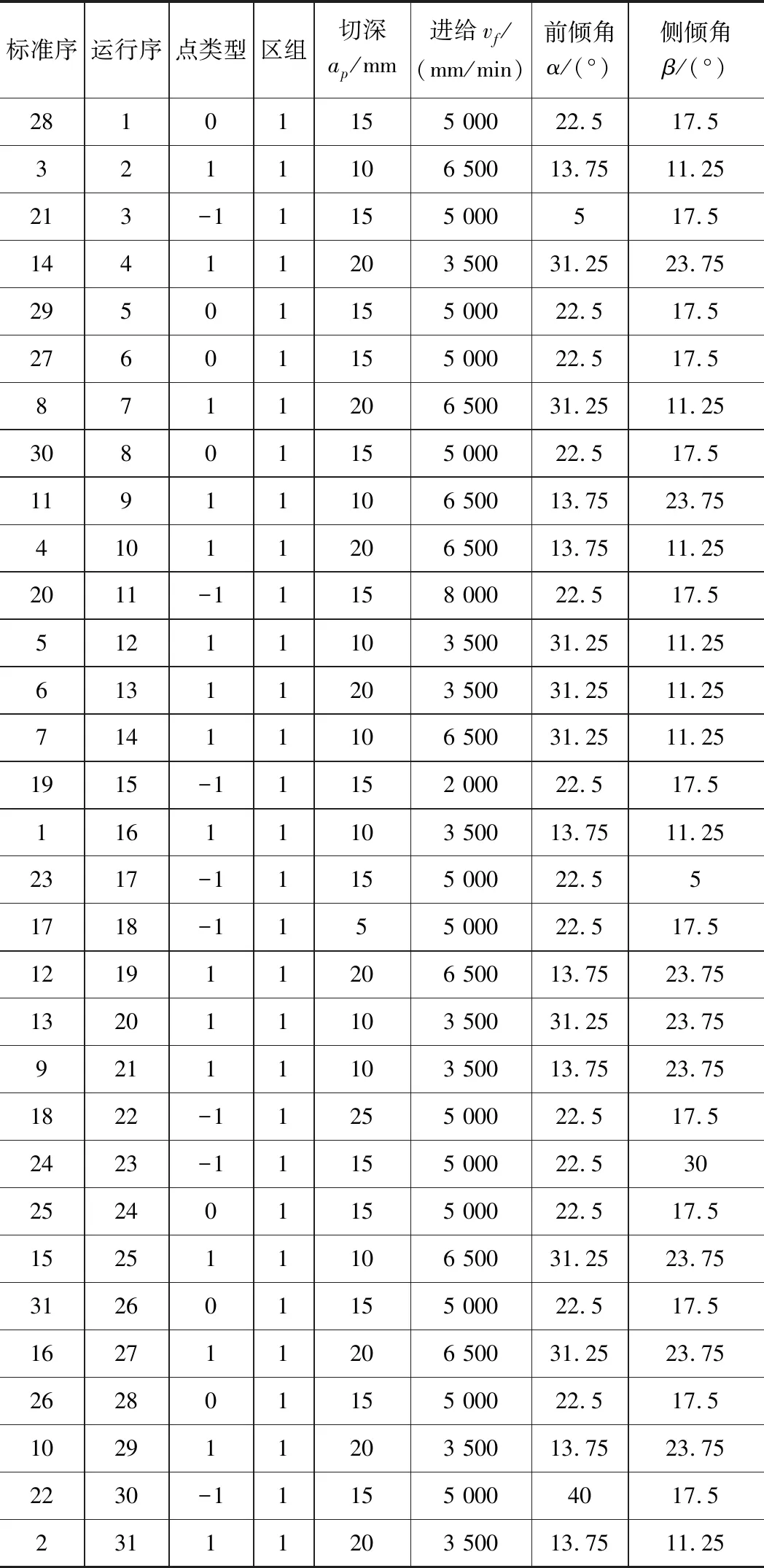
表2 响应曲面实验参数设计表

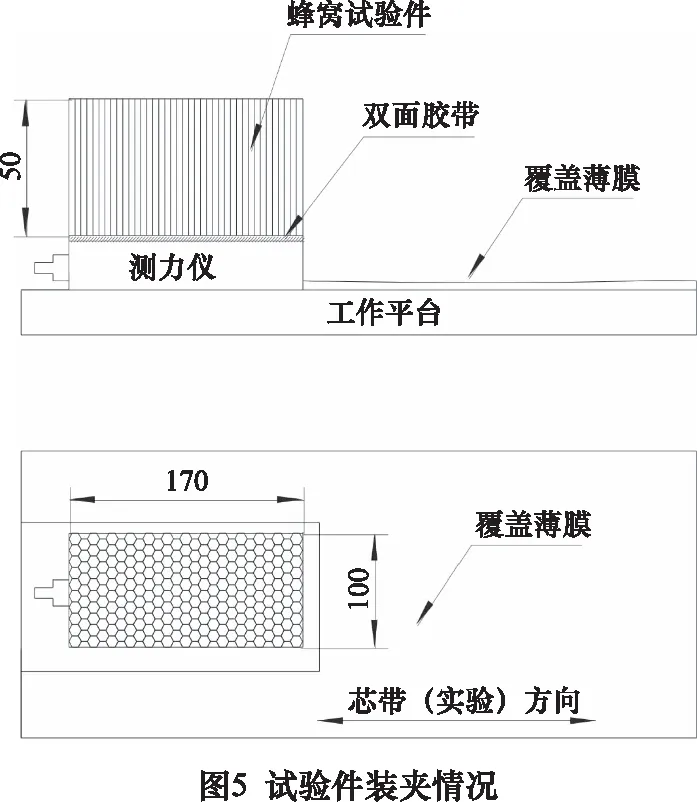
将KISLTER测力仪吸附于机床真空平台上，用双面胶带将蜂窝芯试验件粘贴于测力仪平台上。实验前，为保证切削力准确性，将实验件修面至50 mm的理论高度，再进行实验，试验件装夹如图5所示。

2.3 实验方法

每组实验从左至右(图6所示)进行一次切削，且均沿芯带方向进行，以此规避不同切削位置对切削力的影响。每块试验件进行7组实验，实验主要考察切削深度ap、进给速度vf、刀具前倾角α，刀具侧倾角β四因子对匕首刀切削力Fx、Fy和Fz的影响。切削力的方向定义如图7所示。每个试验件采集一份切削力数据。

3 切削参数对三向切削力影响规律分析

3.1 切削力的滤波处理

匕首刀在加工过程中，附加了20 kHz的高频振动，为了消除此影响并排除实验过程中的其余噪声干扰，需对采集的切削力数据进行滤波。考虑到单组实验中，切割芯格壁时，将引起冲击，此时将引起切削力振动，为保留此冲击振动信息，滤波频率由下式确定：

(1)

式中:l为单组实验的切削长度,mm；score为芯格尺寸,mm;Fmax为最大进给速度,mm/min。

经综合考虑，最后设定滤波频率为50 Hz(低通滤波)，滤波后，单组实验经滤波后的切削力波形如图8所示。

3.2 切削力的漂移修正

在测力仪的使用过程中，发现测量数据有明显的线性漂移(如图9)，随着漂移的累积，将对测量结果产生不可忽略的影响。由于切削力采集设备的配套软件不具有漂移修正功能，因此，需从测量结果中手动滤除漂移值。

(2)

(3)

分别以式(2)、式(3)式来手动进行漂移修正。式中：FmT为切削力修正值,N；FmM为切削力测量值，N；t1、t2为FmM采集的开始时间与结束时间，s；T1、T2为漂移值的采集时间点，s；F1、F2为T1、T2对应的切削力，N；k为漂移的斜率。

修正后，各实验组的切削力统计见表5。

表5 漂移修正后的切削力统计

续表

续表

3.3 三向切削力回归分析

对表5中的数据分别进行Fx、Fy、Fz的回归分析，

Fx=0.01469β2+0.00011apvf+0.02935apβ-

0.01548αβ-1.01871ap-0.00959vf+

0.157α-0.46944β+10.7032

Fy=-0.00453α2-0.01534apα-0.01966apβ+

0.02068ap-0.0003vf+0.29039α+

0.00777β+0.39666

Fz=0.00426α2+0.01287β2+0.01729apα+

0.03064apβ-0.49368ap+0.00037vf-

0.28025α-0.60841β+7.32957

其中，ap为切深，mm；vf为进给速度，mm/min；α为刀具前倾角，(°)；β为刀具侧倾角，(°)。

同时，对所建立的模型进行方差分析，由于Fx的绝对值较小(均值约1 N)，测力仪的测量误差导致采集到的数据相对于真实值有较大的相对误差，因此，Fx的回归结果不理想，Fx回归模型P=0.192>0.05、Fx的回归模型决定系数调整R2=0.21，因此Fx切削力模型对实际加工参数选取的指导意义较弱。

Fy和Fz的回归模型P<0.001，表明Fy和Fz建立的回归模型极其显著；Fy的回归模型决定系数调整R2=0.930 6Fz的回归模型决定系数调整R2=0.912 7,表明Fy和Fz的预测值与试验值拟合程度良好，可以用此模型对匕首刀超声切削Nomex蜂窝材料的切削力的分析和预测。

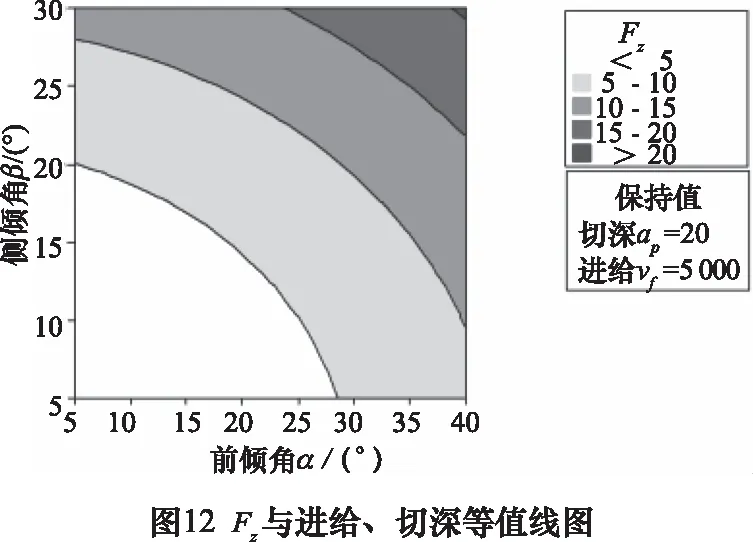
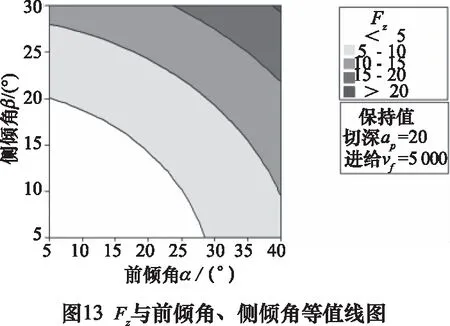
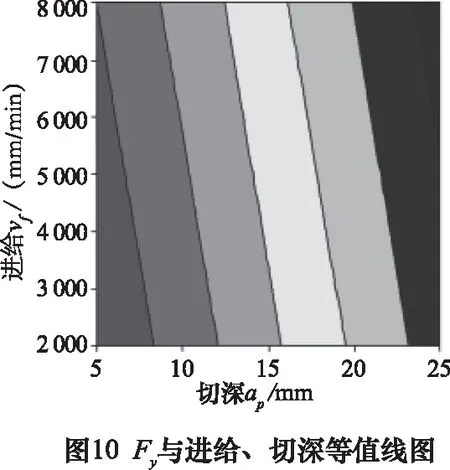
进一步对实验数据作等值线图以更加直接的观测进给、切深、前倾角、侧倾角与切削力的相互作用关系。

由图10～11，随着进给、切深、前倾角、侧倾角的增大，Fy切削力均呈增大趋势，且曲面的梯度较大，说明切削参数对Fy向切削力影响显著，其中切深的影响大于进给速度，侧倾角的影响略大于前倾角。

从图13～14可以看出，随着4个切削参数的增大，Fz切削力同样呈增大趋势，且切深的影响明显大于进给速度，侧倾角与前倾角的影响相当。

4 结语

(1)本文通过匕首刀超声切削Nomex蜂窝芯实验，分析在不同切削深度、进给速度、刀具前倾角，刀具侧倾角下Fx、Fy、Fz的变化情况，以滤波及漂移修正后的数据建立了三向切削力的多元回归方程。Fy、Fz拟合模型可信度高，可用于预测不同切削参数下的切削力。

(2)匕首刀超声切削Nomex蜂窝芯时y向切削力Fy与z向切削力Fz均随着切削深度、进给速度、刀具前倾角，刀具侧倾角的增大而增大。

(3)实际加工时，可尽量减小刀具倾角，特别是侧倾角的大小以降低切削力；减小切深和降低进给速度同样可以降低切削力，若要兼顾加工效率，则应优先提高进给速度。