基于机器学习与群智能算法的精车大螺距螺杆切削优化研究*

李 哲 丛玮琦 付祥夫 田 盛 罗明明

(哈尔滨理工大学高效切削及刀具国家地方联合工程实验室,黑龙江 哈尔滨 150080)

大螺距螺杆类零件广泛应用于重型立式车床以及大型压力机中，起着紧固、连接、传递动力的作用，它的表面质量和精度将影响着机器的加工精度，是影响机床可靠性的重要部件[1]。大螺距螺杆的加工过程中的振动和刀具磨损问题，使得工件表面质量难以保证[2]。

已有研究表明，切削力和切削温度是导致刀具振动与磨损的主要影响因素[3]。本文通过以切削力和切削温度为目标，结合加工效率，进行多目标优化，利用优化的切削参数和刀具参数来抑制刀具的振动与磨损，以期改善工件的表面质量。

庄可佳等[4]建立了切削力和材料去除率的预测模型，以最大材料去除率和最小切削力为优化目标，得到最优切削参数组合，实现了钛合金插铣高效稳定加工的目的。鲁娟等[5]应用支持向量机和BP神经网络结合的方法构建了铣削蠕墨铸铁表面粗糙度的预测模型，并对模型的预测精度进行验证，可以很好地对表面粗糙度进行预测。刘洋等[6]利用神经网络建立钻削过程中切削力与切削参数之间的关系模型，与多元线性回归建立的模型相比，神经网络建立的模型预测精度更高。卢明明等[7]为了抑制三维椭圆振动切削过程中刀具的振动，改善工件的表面质量，建立表面质量与切削参数之间的数学模型，应用改进后的人工蜂群算法进行切削参数优化，得到更优的工件表面质量。马廉洁等[8]采用粒子群算法改进BP神经网络，建立了切削力、刀具利用率的优化目标函数，经过求解后进行实验验证，证明参数优化结果有效。Wang Z G等[9]采用遗传算法对切削过程中材料去除率和表面粗糙度进行多目标优化，得到了最佳工艺参数，降低了工件的表面粗糙度。

以上学者在预测模型建立以及切削优化方面的研究给予本文启示，对于建立精车大螺距螺杆切削力、切削温度的回归预测模型以及后续的参数优化具有参考意义。本文采用基于机器学习方法，以切削参数与刀具参数为变量，建立切削力和切削温度模型。用群智能算法对建立的模型进行优化求解，最后对优化结果进行实验验证。

1 切削实验及数据提取

1.1 大螺距螺杆精加工车削工艺分析

通常将螺距大于4 mm称为大螺距螺纹，本文进行研究用到螺杆的螺距为18 mm，为了使切削力在切削刃上均匀分布，降低切削过程中振动的影响，大螺距螺杆在精加工阶段采用轴向分层切削工艺，轴向分层切削时左刃或右刃全部参与切削。精车大螺距螺杆工艺如图1所示。

图1中，n为主轴转速，vf为轴向进给速度；ap为切削深度，P为螺距，D1、D2和D分别为工件螺纹的小径、公称直径和大径，Zli、Zri为左、右刃单次加工余量，hDl、hDr为左、右刃单次加工时的切削厚度，bDl、bDr为左、右刃单次加工时的切削宽度，krl、krr分别为左、右刃切削时的主偏角。

1.2 实验材料及设备

大螺距螺杆采用CAX6140车床进行加工，工件的材料为45#钢，相关参数如表1所示，所用的刀具材料为W18Cr4V成型车刀，刀具参数如表2所示，刃口形状为钝圆刃，其中刀具后角以及刃口半径在表3中给出。通过相关研究可知，刀具前角和刃倾角的变化对于切削力、刀具变形以及牙型精度存在影响，同时考虑到刀具的耐磨性和强度这两个因素，最终确定刀具前角和刃倾角为0°时最能满足生产加工的实际要求，不需要对其角度进行优化[10]。

表1 大螺距螺杆尺寸

表2 刀具参数

实验所采用的设备如图2所示，使用DHDAS5922动态信号测试系统对切削力信号进行采集，用到的传

感器为PCB三向传感器，通过THERMO VISION A40

热像仪对切削区的切削温度进行测量。

1.3 实验方案及结果

通过切削实验获取不同参数条件下的切削力、切削温度数值，考虑到切削参数和刀具参数的切削方案如表3所示。

表3 正交试验因素水平表

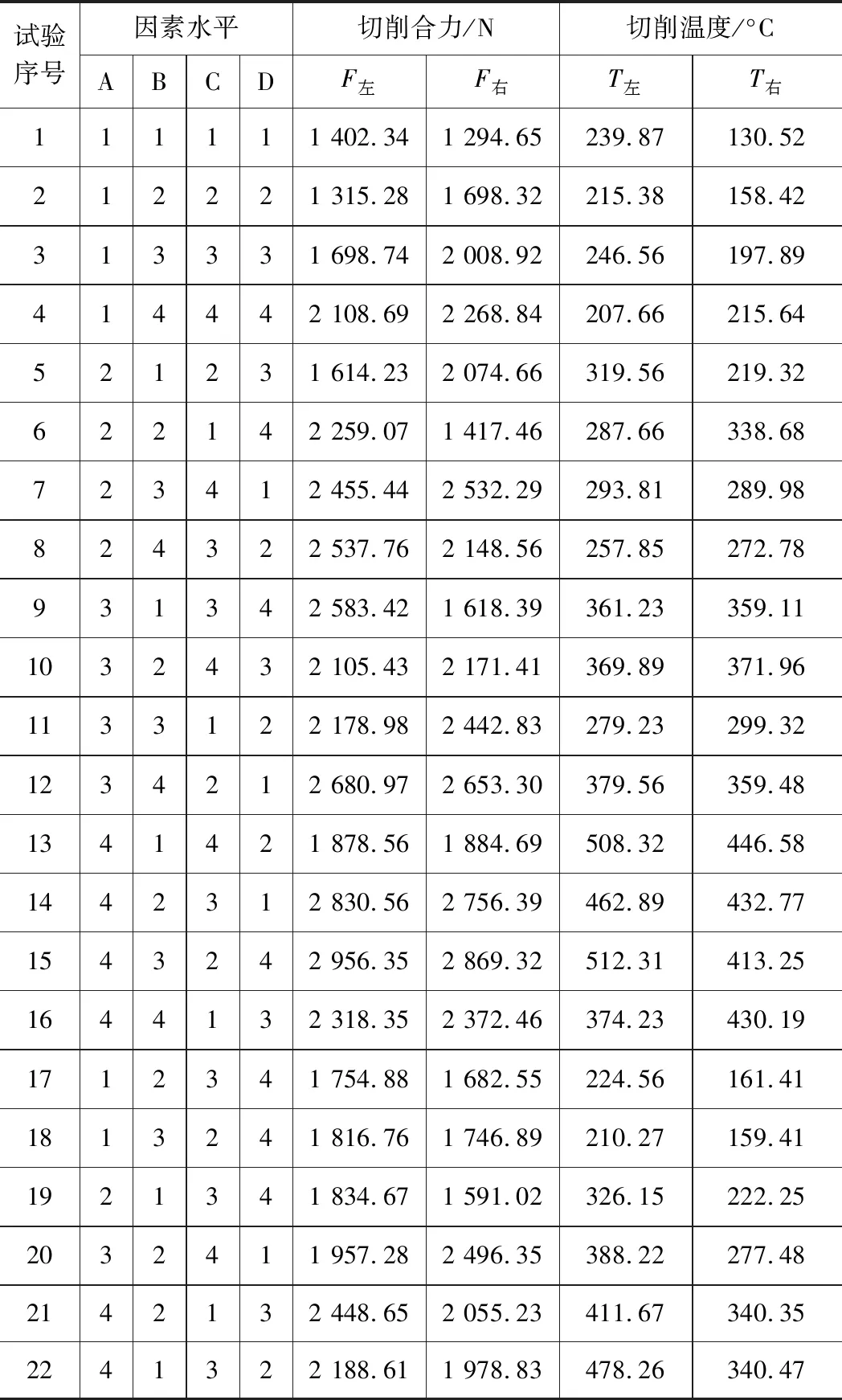
表4 实验数据表

建立对应的切削参数与切削力、切削温度的正交表，如表4所示，其中编号1～16为正交试验组，用于回归模型的建立；编号17～22为不同于正交试验组的切削方案，作为预测组，用于对模型的预测效果进行检验。F左为左刃受到的切削合力，简写F左。

2 切削力与切削温度建模

2.1 支持向量机回归建模

支持向量机(SVM)可以用来解决分类以及回归建模的问题，通过不同的核函数类型而完成对数据的回归分析，建立输入量与输出量之间的关联模型。经过对各项参数不同时的回归效果进行比较，选用支持向量机的类型为ε-SVR，核函数类型为多项式核函数，设置ε-SVR的损失函数C的值为默认值1，损失函数w的值为0.1，核函数中的gamma函数的值为1。

2.2 回归结果比较

为了证明机器学习在回归分析中的精准性，同时采用传统的回归方法对数据进行拟合，获得经过不同方法得到的切削力、切削温度的拟合及预测情况如图3和图4所示。

得到切削力、切削温度的拟合误差分析如表5，表6所示，其中包括拟合与预测的平均误差与最大误差。

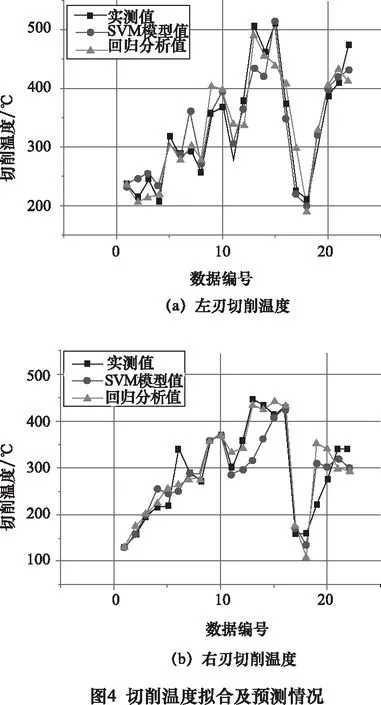
表5 切削力拟合误差分析表

表6 切削温度拟合误差分析表

经过上述分析最终确定，支持向量机拟合后得到的模型更优，拟合与预测精度高，可以更好地反映切削参数与切削力、切削温度之间的关系。

3 基于群智能算法的参数优化

3.1 多目标优化方程的求解

多目标优化中的难点是目标间的权重分配问题，本文基于MATLAB软件，编写出含有Pareto最优解的人工蜂群算法与粒子群算法的程序。多个目标同时处于最优解时即为Pareto最优解，也就是指资源分配的一种理想状态。处于这种状态下的解集为资源的最优分配，如果在这时想获得某个目标的更优值，则会破坏资源分配的理想状态，进而导致其他目标不再是最优解[11]。本文就是基于Pareto最优解理论进行的参数优化，解决了在多目标优化存在的目标间冲突的问题。

结合切削实验以及以往切削加工中常用的参数范围，最终确定参数优化的约束条件如下：

(1)主轴转速约束条件：10 r/min≤n≤25 r/min。

(2)轴向进刀量约束条件：0.05 mm≤f≤0.125 mm。

(3)刀具后角约束条件：5°≤α≤9°。

(4)钝圆刃口半径约束条件：0.04 mm≤R≤0.10 mm。

将切削力与切削温度作为优化目标，与此同时还需要考虑到材料去除率这一指标[12]。材料去除率如式(1)所示，最终确定优化目标方程如式(2)和(3)。

Q=v×ap×f

(1)

式中:v为切削速度，ap为切深，D为工件直径，n为主轴转速，v=π×D×n/1 000。

(2)

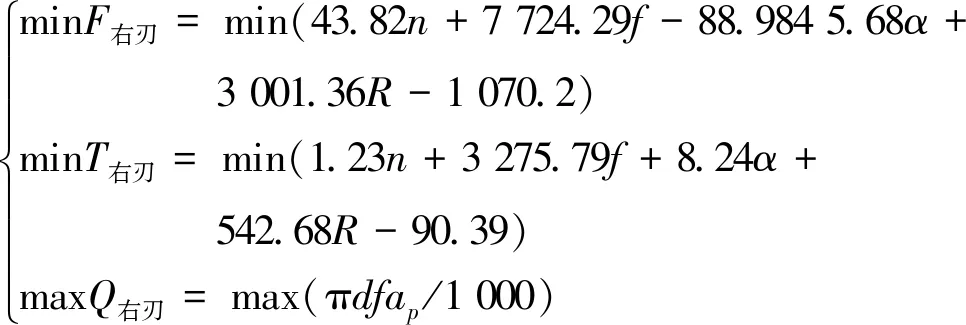
(3)

采用人工蜂群算法和粒子群算法进行多目标优化求解，算法相关参数的设置如表7所示。

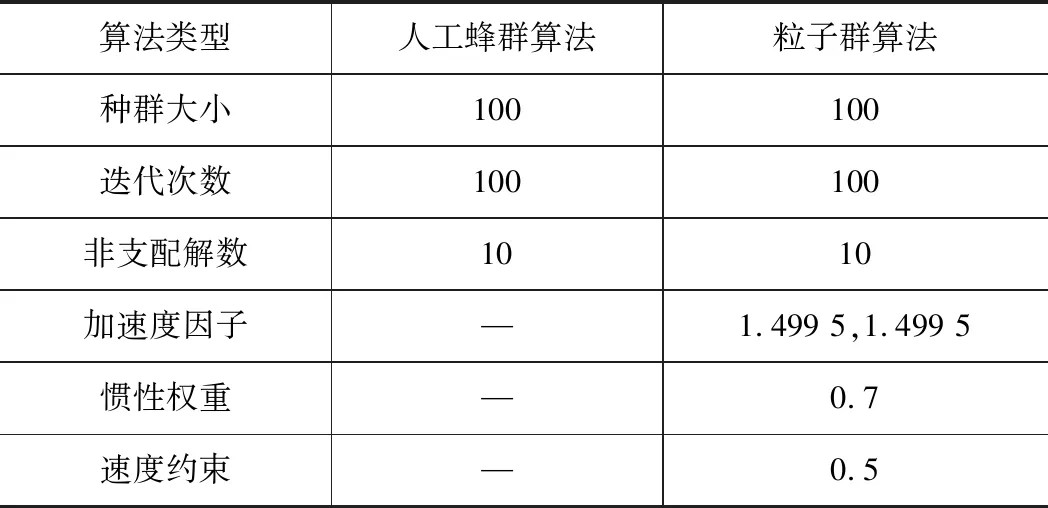
表7 算法相关参数

3.2 优化结果比较

经过参数优化求解后，得到人工蜂群算法和粒子群算法求解出的Pareto前沿分布如图5和图6所示。

从二者的Pareto前沿分布图中，提取出对应的前沿值，对不同算法的求解性能进行比较，采用求解时间、MID和SNS值3个指标进行评价，其中MID[13]代表Pareto前沿值与最小理想适应度值(0,0,0)的距离，SNS代表非支配解的分散水平，计算公式如(4)和(5)所示。

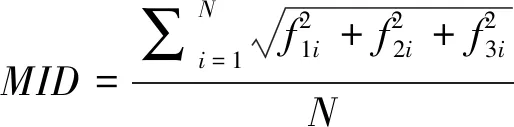
(4)

(5)

式中：N代表非支配解的个数，f1i、f2i、f3i代表Pareto前沿值中，第i个非支配解的3个适应度值。MID的值越小越好，该值越小，表明Pareto前沿值更靠近最理想适应度值。SNS表示Pareto非支配解的分散程度，数值越大，说明Pareto前沿值越分散。

经过计算后，得到两种算法的各项性能指标如表8所示。

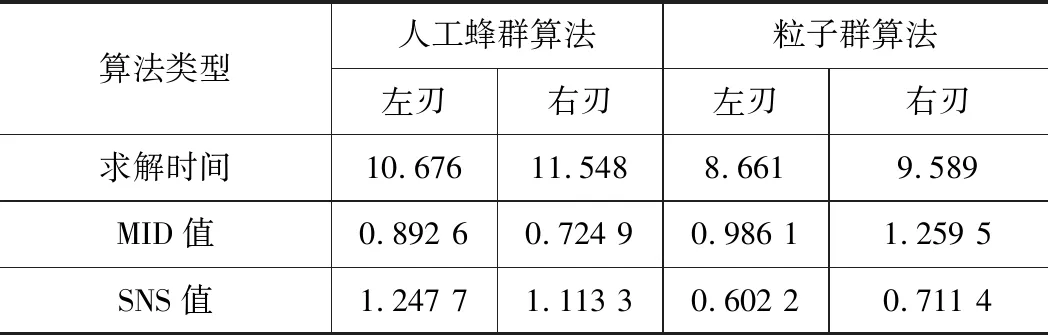
表8 算法的性能指标

最终选择性能相对较好的人工蜂群算法求解出的参数作为精车大螺距螺杆的最优切削参数。确定左刃切削最佳参数为：转速n=20 r/min，进给量f=0.05 mm，刀具后角α=6°，刀具刃口半径R=0.06 mm；右刃切削最佳参数为：转速n=16 r/min，进给量f=0.05 mm，刀具后角α=6°，刀具刃口半径R=0.04 mm。

3.3 验证实验

为了验证优化得到刀具参数和切削参数的有效性，需进行验证实验。工件参数和刀具参数如表1和表2所示，实验仪器如表3所示，经过优化后的刀具参数(后角、刃口半径)以及切削参数得到了更有效的值，相关参数在表9中列出。具体的切削方案如表9所示，其中方案一的刀具参数经过优化，方案二的切削参数经过优化，方案三为刀具结构和切削参数优化后的最优值，方案四为上文正交实验方案中的参数，以此作为对照，对优化效果进行验证。

对加工完的工件进行取样处理，沿着轴线方向，从切入端向切出端依次标记，利用线切割机床将标记样块取下，利用超景深显微镜测量其左右螺纹面的表面粗糙度值，通过采集多次测量数据，对每个取样的粗糙度值求取平均值，最终获取螺纹面粗糙度参数测量结果。如图7所示为螺杆表面粗糙度的测量方法。

表9 切削方案

提取出测量得到的表面粗糙度数值，得到不同切削方案下的样块左、右螺纹面粗糙度值，如图8所示。

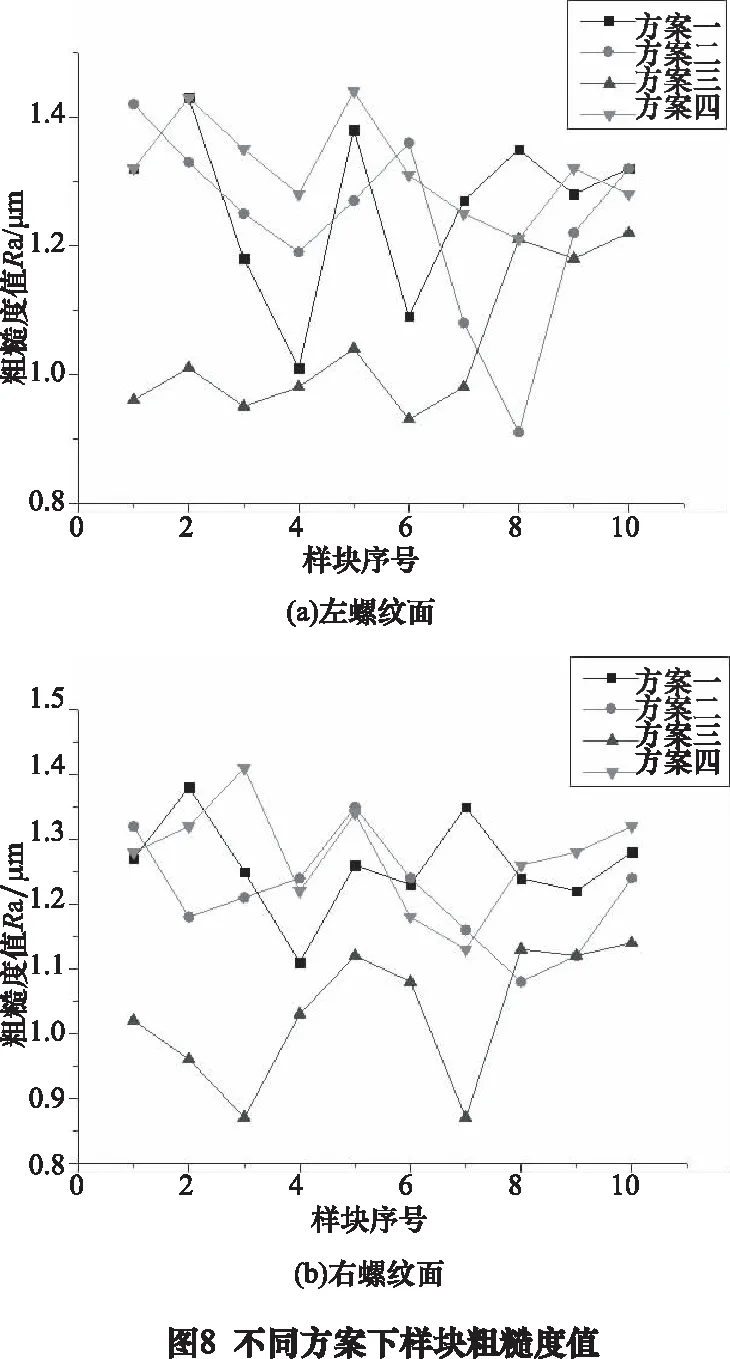
不同切削方案下左右螺纹面粗糙度平均值如图9所示。

对通过不同切削方案得到的工件样块表面粗糙度平均值分析可知，经过切削参数优化后的方案三，获得的工件样块表面粗糙度值更小，证明切削优化有效，经过切削优化后得到的工件表面质量得到改善。

4 结语

(1)运用支持向量机算法，对不同切削参数对应的切削力、切削温度数值进行训练，建立了拟合精度更高的回归预测模型。

(2)采用人工蜂群算法与粒子群算法对切削力、切削温度、材料去除率的多目标优化方程进行求解，得到切削参数和刀具参数的最优值；通过对不同算法的求解时间、MID值、SNS值这3项性能指标进行比较，确定人工蜂群算法的优化结果为最优解。

(3)进行精车大螺距螺杆验证实验，对获得的工件表面粗糙度的测量结果进行对比，发现选用优化后的参数进行加工，工件表面粗糙度降低了20%，可以获得更好的工件表面质量。