基于两阶段启发式算法的公路网布局研究

常馨玉

（交通运输部科学研究院，北京 100029）

0 引言

公路运输作为综合运输体系的重要组成部分，对社会发展和客货流通具有非常重要的作用。随着公路网规模的不断扩大、等级结构的不断提升，部分区域路网布局不够合理等问题日益凸显。例如，某些路段交通量过饱和，造成通而不畅；有些节点间缺乏多路联通，路网的韧性和安全性有待提升，这些问题都影响了公路网整体效益的发挥。为此，需对公路网布局方法进行研究，通过完善已有的公路网布局方法为规划实践提供理论指导。

在公路网布局方法方面，国外主要使用专家论证法、数理解析法、系统分析法和四阶段法[1]。随着计算机技术的广泛应用和交通规划的不断发展，一些研究逐渐将公路网布局问题看成网络优化问题来分析[2-3]，即在一定的约束条件下以目标函数最优为目的，通过求解决策变量来获得最优解。国内对交通规划的研究起步相对较晚，最初采用专家论证法和数理解析法，后又采用四阶段法等交通规划理论和模型。随着我国交通规划的发展，国内学者结合我国国情对公路网布局做了进一步探索。目前，我国公路网布局方法主要有以下4 种：总量控制法、节点重要度法、四阶段法、交通区位线法，这几种方法在实践中得到了广泛应用。在此基础上，一系列研究工作也相继开展，主要分为4 类：①通过定性分析与定量分析相结合来改进现有布局方法，如节点重要度结合交通区位线法的联合布局法[4-6]、改进的线路重要度模型[7-8]、改进的节点重要度法[9]等；②分析路网布局的影响因素，对各相关因素进行量化并引入模型，构建多因素布局优化模型[10-12]；③基于图论，考虑运输需求、节点重要度、区域经济联系度等建立多目标混合整数规划模型[13-15]优化公路网布局，通过对抽象网络的布局来指导实践规划；④基于GIS 技术，实现规划过程的可视化，构建基于ArcGIS 软件平台的路网规划模型[16-18]。

在算法求解方面，已有研究通过构建启发式算法对复杂的网络布局问题进行求解。Du 等[19]运用衰退可靠性模型和求解算法，对交通需求和路段流量变化进行分析预测；Solomon[20]应用节约算法、扫描法等启发式算法求解路径优化问题；余健[21]基于遗传算法，针对具有两个约束条件的情况，提出线路的最优或次优解决方案；赵会艳等[22]构建了高速公路物流网络规划模型，并运用改进遗传算法求解，提高了计算效率；吴群琪等[23]提出添加虚拟节点的方法对公路网布局进行优化，并引入粒子群算法对模型求解；蔡锦德等[24]综合考虑建设费用、路网可靠性和对环境的影响3 个因素构建了多目标路网规划模型，并设计混合粒子群优化算法求解模型；杨明等[25]构建了随机OD 需求下的双层交通网络规划模型，设计了基于Frank-Wolfe算法等的遗传算法求解。

可以看出，既有研究针对公路网的布局方法较为单一，多集中于对既有方法（如节点重要度法、四阶段法）和模型的优化改进，且求解算法多采用单一阶段的路径优化算法，缺少对初始解二次优化的过程。本文将基于既有研究，结合节点重要度法，综合考虑节点的运输需求、路段重要度等因素构建混合整数规划模型，并采用随机游走算法和模拟退火算法相结合的两阶段启发式算法对模型进行求解，以期使公路网布局方案更合理。

1 路网布局模型构建

1.1 问题描述

在进行公路网布局研究时，会将实际的公路网抽象为节点间的连线，节点间的需求是有向的，但本文重点解决在满足需求的基础上实现抽象网络中节点间的连通问题，而非确定交通流向。因此本研究将问题定义在无向图中，求解在多种约束条件下满足节点连通节点间客货流双向联系的公路网布局方案。既有的公路网布局多从旅行时间、建设费用、运输成本等角度来建立模型并对网络进行优化，本文以公路网总旅行时间最小作为目标，以带权邻接矩阵作为目标函数路网总旅行时间的决策变量，通过目标函数和约束条件之间相互影响、相互反馈对带权邻接矩阵（0-1变量）不断进行优化，最终获得最优目标函数下的带权邻接矩阵，以此得到相应的公路网布局方案。

1.2 模型构建

将问题定义在无向图G=(V,S)上，V表示n个节点的集合，V={1,…,n} ；S表示路径集合，s表示路径，s∈S。

目标函数为求公路网总旅行时间最小：

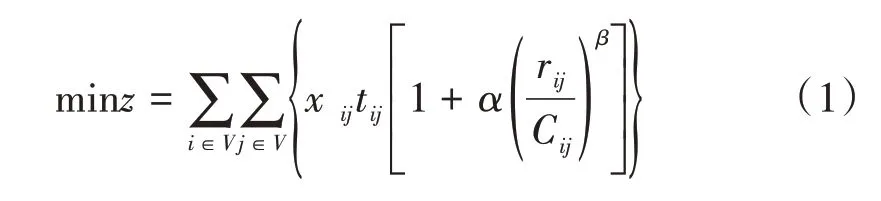
式（1）中：z为公路网总旅行时间；xij为0-1 变量，当节点i,j（i,j∈V）间有直线连通时取1，否则取0；tij为节点i,j间的旅行时间；rij为由i点到j点的公路客货运输需求量；Cij为路段运输承载能力；α,β为模型参数，在美国联邦公路局的交通分配程序中，取α=0.15,β=4。

目标函数的约束条件如下：

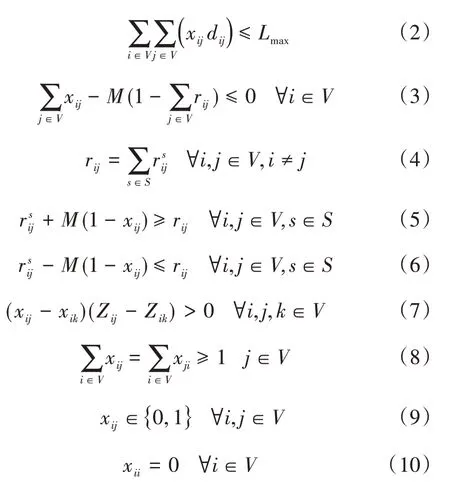
约束（2）表示公路网的里程规模不超过里程规模上限，实际规划过程中可结合当地建设需求以及数理模型预测来确定，其中Lmax表示交通网络的里程规模限制，dij表示从节点i到节点j的直线距离；约束（3）表示所有节点的客货运输需求均被满足，其中M表示一个能使不等式恒成立的较大的数；约束（4）表示由i点到j点的多条路径客货运输需求之和为i点到j点的客货运输需求，其中表示由i点到j点的通过路径s的公路客货流量；约束（5）和（6）表示若i点到j点是直线连通，则i点到j点的公路客货运输需求总量等于由i点到j点通过路径S的公路客货流量；约束（7）表示当节点i与节点j间的路段重要度大于节点i与节点k间的路段重要度，那么xij=1,xik=0，反之，xij=0,xik=1，其中Zij表示节点i,j间的路段重要度；约束（8）表示每个节点都被连接且每个节点多路连通；约束（9）表示xij是0-1变量；约束（10）表示当节点i=j时，xij=0。

2 随机算例设计

为验证模型和算法的有效性，本文利用MATLAB 生成随机算例，算例的编号为RANDn，表示节点个数为n的随机算例。

（1）生成公路网中节点的位置坐标和运输时间矩阵

首先，建立笛卡尔坐标系，将抽象网络中的节点位置表示在坐标系中。将本次公路网的覆盖范围设定为100km×100km，以（50,50）为圆心，50 为半径生成圆，在该圆内随机生成n个客户点坐标，利用各节点的坐标计算两节点间的欧氏距离dij，除以牵引车的旅行速度v即可得到两节点间的旅行时间tij，计算公式为：

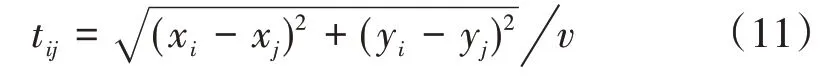
式（11）中：(xi,yi),(xj,yj)分别为两节点的空间位置坐标。

（3）生成节点i,j间的路段重要度Zij矩阵以及路段运输承载能力Cij矩阵

在MATLAB 中生成一个n阶的零矩阵，生成(n2-4)/2 个随机数，并将随机数赋值于[Z12,…,Z1n],[Z23,…,Z2n],…,，生成矩阵，将矩阵转置后得到矩阵，将矩阵和矩阵相加后得到路段重要度矩阵Zij。在MATLAB 中生成n×n的随机数矩阵作为路段运输承载能力矩阵Cij。

3 两阶段启发式算法设计

网络布局问题属于NP-hard 问题，通常采用启发式算法求解，启发式算法是一种仿自然体算法，针对很多难以求解的复杂问题可给出相对满意的可行解。常见的启发式算法主要有节约算法、邻域搜索、蚁群搜索、遗传算法、随机游走算法等，既有针对网络布局问题的研究多采用邻域搜索、蚁群算法、遗传算法等，采用随机游走算法求解网络布局问题的较少。随机游走算法是一种局部搜索算法，其基本策略是每次从当前候选解的邻域中选择一个更优的进行转移，相较于邻域搜索、遗传算法等能在全局优化的过程中避免陷入局部极小值。本研究构建的初始路网具有无规则性，若采用随机游走算法求解，随着迭代次数的增加，可能会陷入局部最优点，因此本文在用随机游走算法求得初始解的基础上结合模拟退火算法，对初始解进行再次优化，允许在迭代过程中以一定的概率接受较差的解，摆脱局部最优情况。采取随机游走算法和模拟退火算法相结合的两阶段启发式算法能增强算法的全局搜索能力，提高获得最优解的概率。

3.1 随机游走算法

由于模型中要计算节点间的旅行时间，因此在优化过程中，实际改变的决策变量是各节点间的带权邻接矩阵，而计算两节点间的最短距离可采用Dijkstra 算法。该算法使用贪心算法策略，用于计算一个节点到达另一个节点的最短路径，在本文两阶段启发式算法中属于内层嵌套算法。Dijkstra 算法流程如图1 所示，其中w(k,j) 表示从k到j的路径长度。

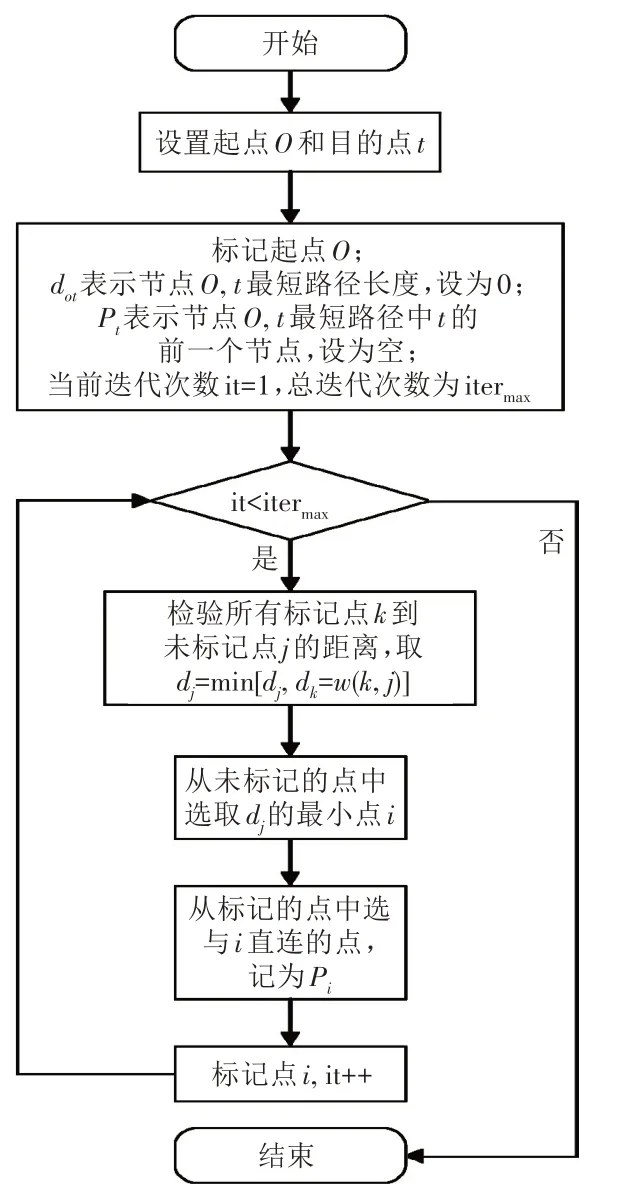
图1 Dijkstra算法流程图

外层的随机游走算法用来优化带权邻接矩阵xij。首先，根据公路运输需求矩阵生成邻接矩阵xij_b来表示节点间的连通情况，该邻接矩阵不唯一，节点间有多种连接情况来满足运输需求，相应得到多个邻接矩阵xij_b下的目标函数值object_b。在邻接矩阵xij_b的基础上做随机扰动，如随机改变节点i,j的连接（若i和j连通，那么断开，反之建立连接），通过随机操作后能得到一个新的邻接矩阵xij_n，计算当前邻接矩阵xij_n下的目标函数值object_n，若object_n＜object_b，则接受新的邻接矩阵xij_n，若object_n≥object_b，则不接受该次扰动，重新进行下一次寻优。由于邻接矩阵xij_b的生成具有一定的随机性，因此，在此基础上的随机扰动大概率会使得当前解优于初始解，当达到初始设定的迭代次数后，输出当前的目标函数值T即为最大迭代次数下的最优解。随机游走算法流程如图2所示。

图2 随机游走算法流程图

3.2 模拟退火算法

模拟退火（Simulated Annealing,SA）算法利用组合优化问题与物理退火过程间的相似性，使优化过程从某一较高初温（即初始解）开始，迭代过程伴随温度（即目标值）的不断下降，并结合温度在短期内小幅度上升（即随机接受较差解）的特点，能跳出局部最优解，在解空间中随机寻求全局最优解。本研究采用模拟退火算法对随机游走算法生成的初始解进行优化，使其在迭代过程中能以一定的概率接受较差解，从而使算法能跳出局部最优，改进计算效果。接受较差解的概率P可以随着迭代次数的增多而降低，P=(1-i/Iter) × Rand2，其中，i表示当前迭代次数，Iter表示最大迭代次数，Rand2为生成的随机数。

模拟退火算法流程如下。

步骤1：设置最大迭代次数Iter，以随机游走算法获得的解为初始解，开始迭代。

步骤2：若i＜Iter，则返回随机游走算法重新求解初始解，并得到目标函数值T，进行步骤3。否则，转到步骤4。

步骤3：设当前解的目标值为CUR，若T＞CUR，则将初始解T设为当前解；若T≤CUR，生成随机数Rand1，Rand1为[ ]0,1 的随机数。当Rand1＜P时，T为当前解；否则当前解不变，迭代次数加1，返回步骤2。

步骤4：将当前解设为最优解，计算终止。

历史最优解不受模拟退火的影响，只有寻优到新的最优解时才会覆盖原有解，当出现新的最优解时更新节点连接网络。在达到最大迭代次数后算法停止并输出最优解。

模拟退火算法流程如图3所示。

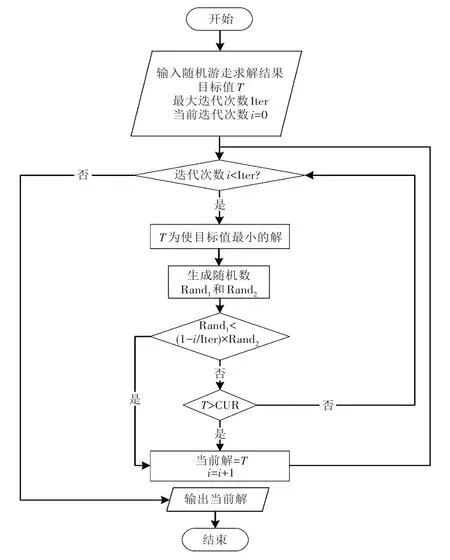
图3 模拟退火算法流程图

4 算例求解与分析

本文运用两阶段启发式算法对生成的随机算例进行求解，以区域内10个节点的算例为例进行连线布局，节点间的时间矩阵、路段重要度矩阵、客货运输OD 流量矩阵和路段运输承载能力矩阵分别如表1～表4所示。

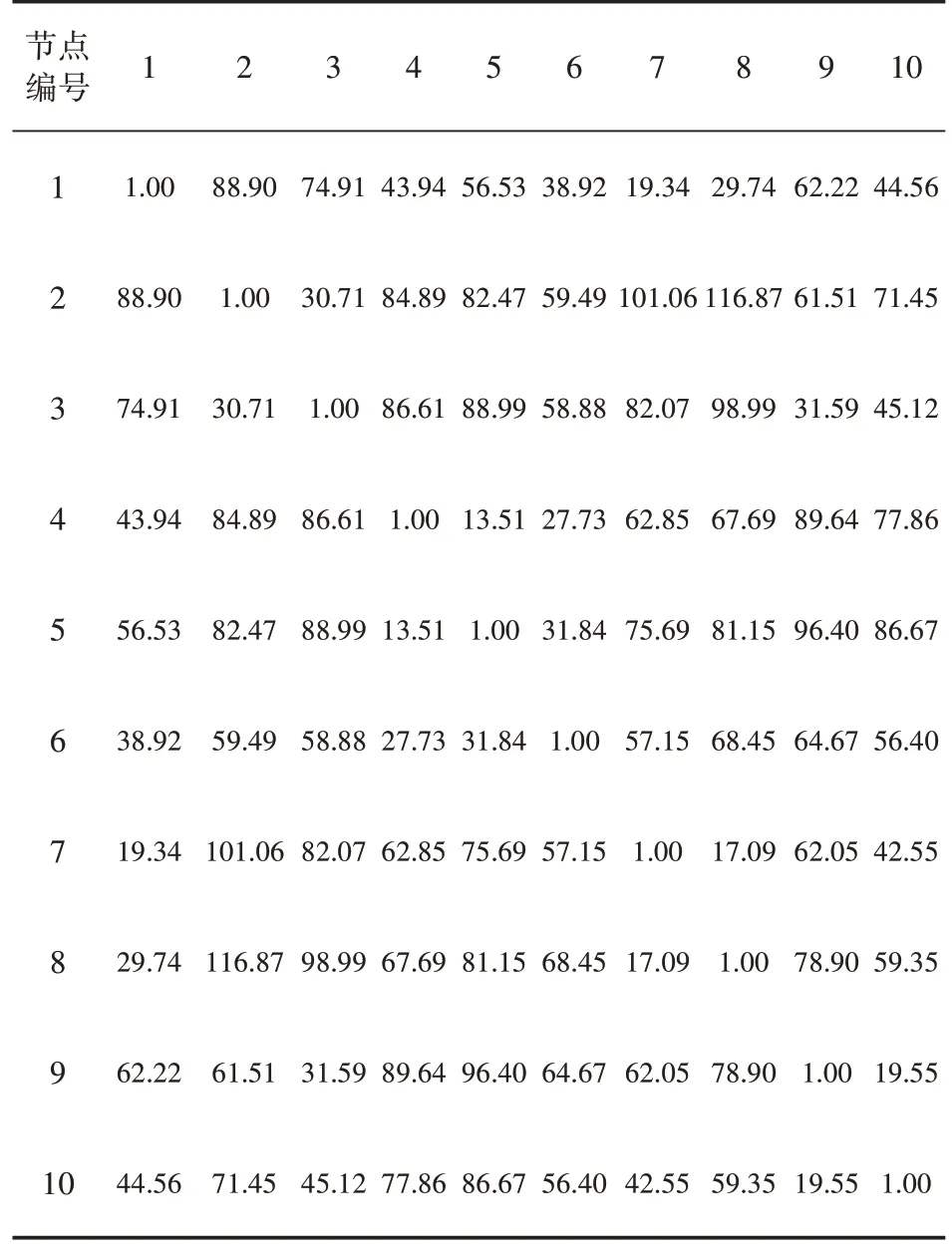
表1 节点间时间矩阵tij 单位：h

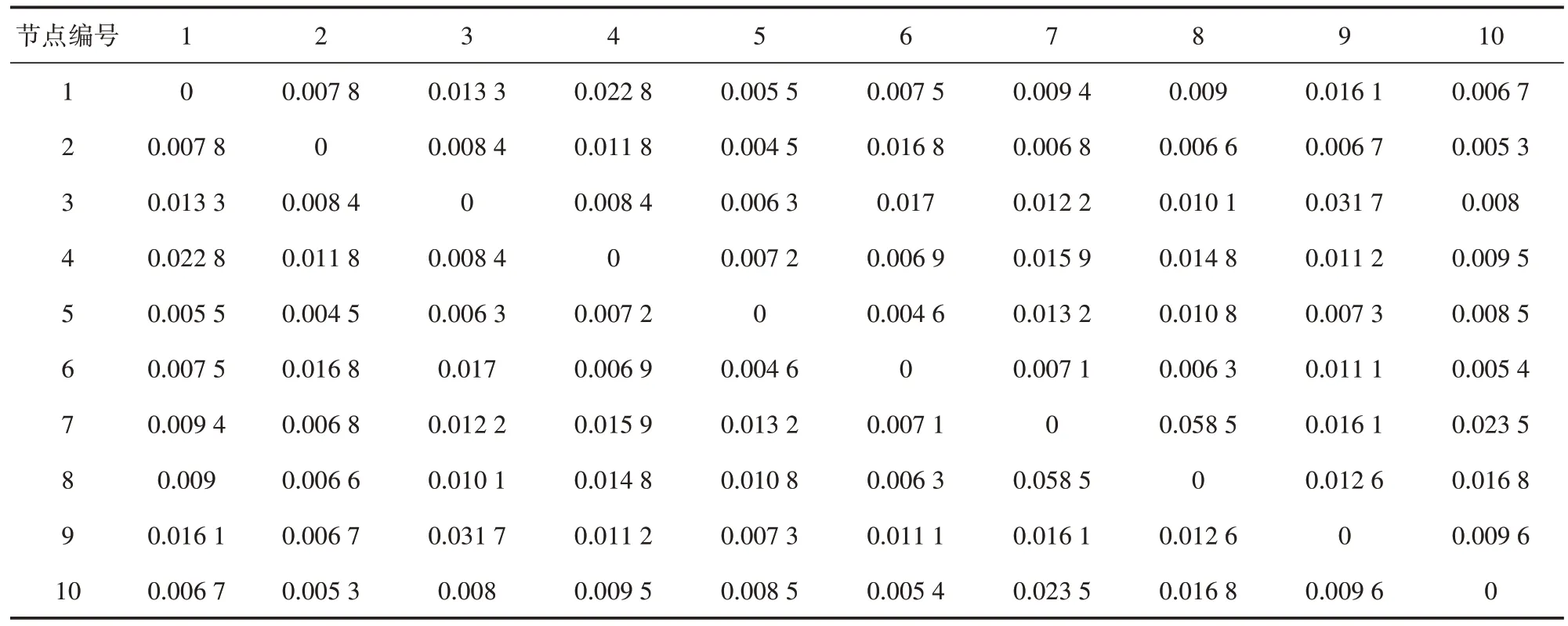
表2 路段重要度矩阵Zij

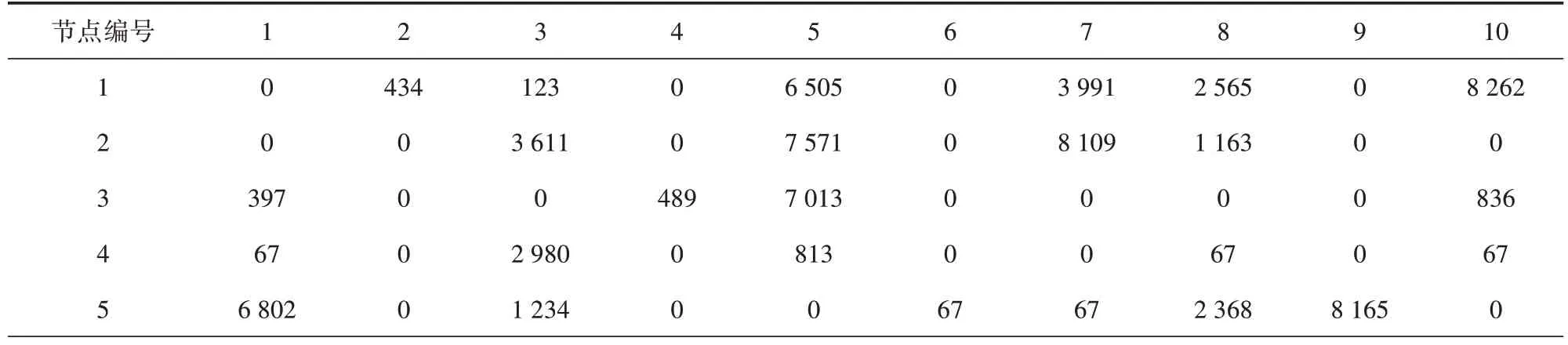
表3 客货运输OD流量矩阵rij 单位：kg

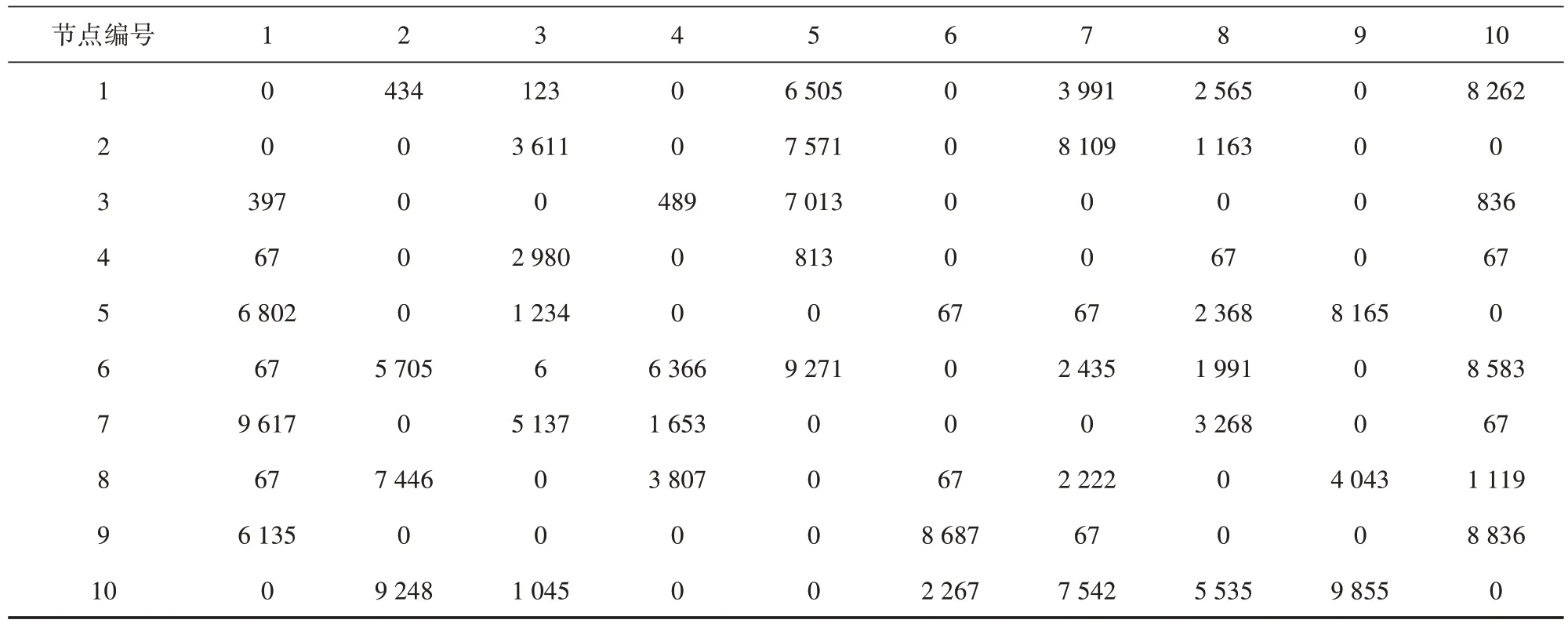
表3 （续）

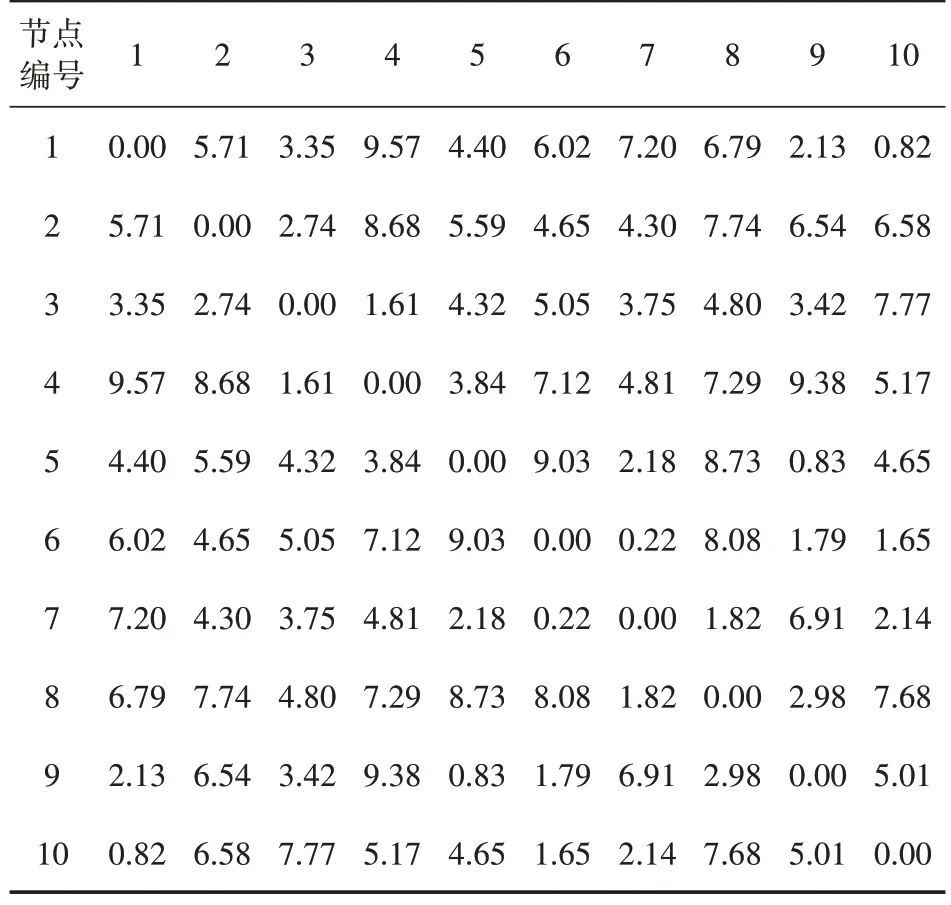
表4 路段运输承载能力矩阵Cij 单位：kg

通过MATLAB 编程计算，循环次数设置为5 000，每次循环中在生成初始解的基础上按照一定的概率接受较差的解，直至所有节点均被连通，由此得到目标函数值z=54.45h，计算时间为15s。各节点的布局连接情况如表5所示。

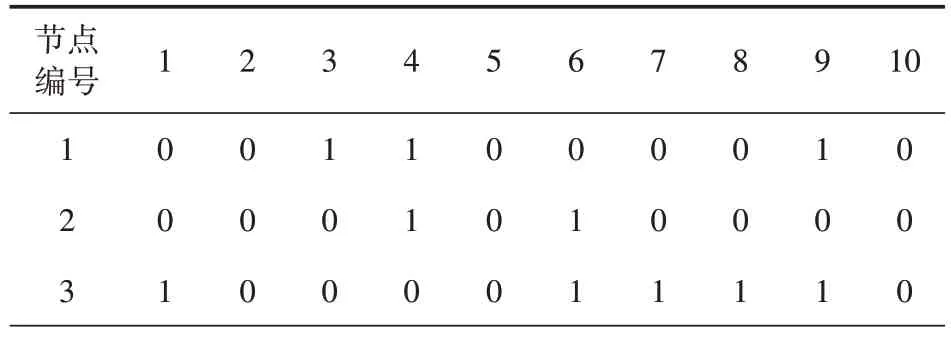
表5 节点间布局连接情况

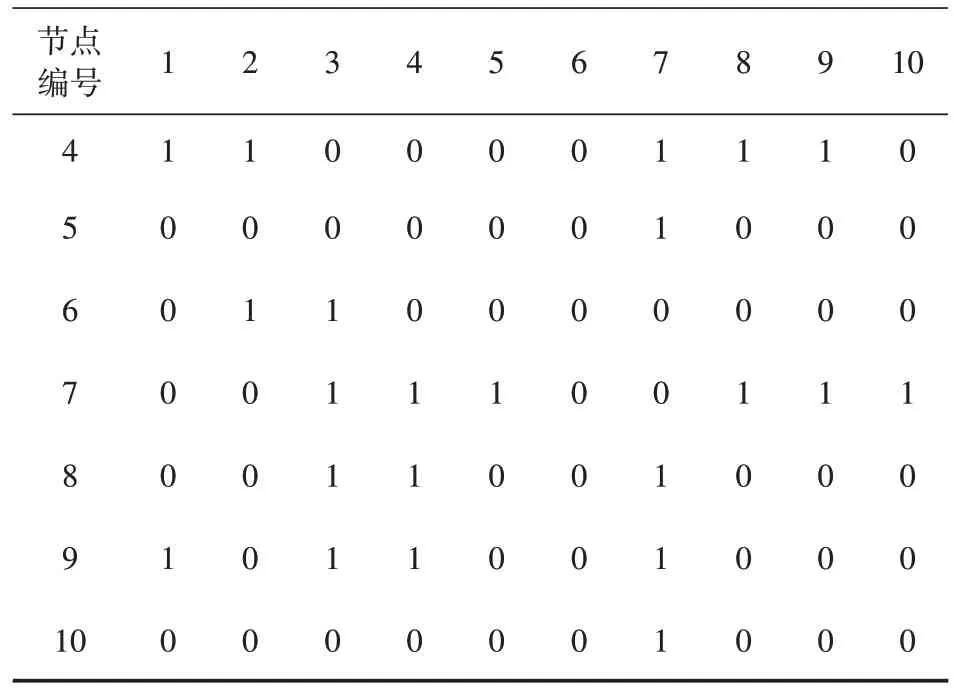
表5 （续）

通过对随机算例的求解得到图4节点连通图，节点的空间位置由横纵坐标确定，图4 反映了两个节点间的连通情况，可代表一条线路，也可代表多条线路之和。由图4 可以看出，当迭代次数较少时，优先连通重要度较大的节点，部分重要度较低的节点尚未被连通（如图4（a）所示），随着迭代次数的增加，网络中的所有节点均被连通（如图4（b）所示）。当给一定的随机扰动后，节点间的连接情况发生改变，重要度较低的节点可能被多路连通，若目标函数值未被优化，那么重新改变连通方式（如图4（c）～4（f）所示），直至在最大迭代次数下获得目标函数值最优的公路网布局方案（如图4（g）所示）。图中存在节点4 到节点7、节点5 到节点7 的连线接近重合的情况，原因为该图是抽象网络图，图中两条连线仅反映节点间的连通情况，连线接近并不代表实际路线接近。

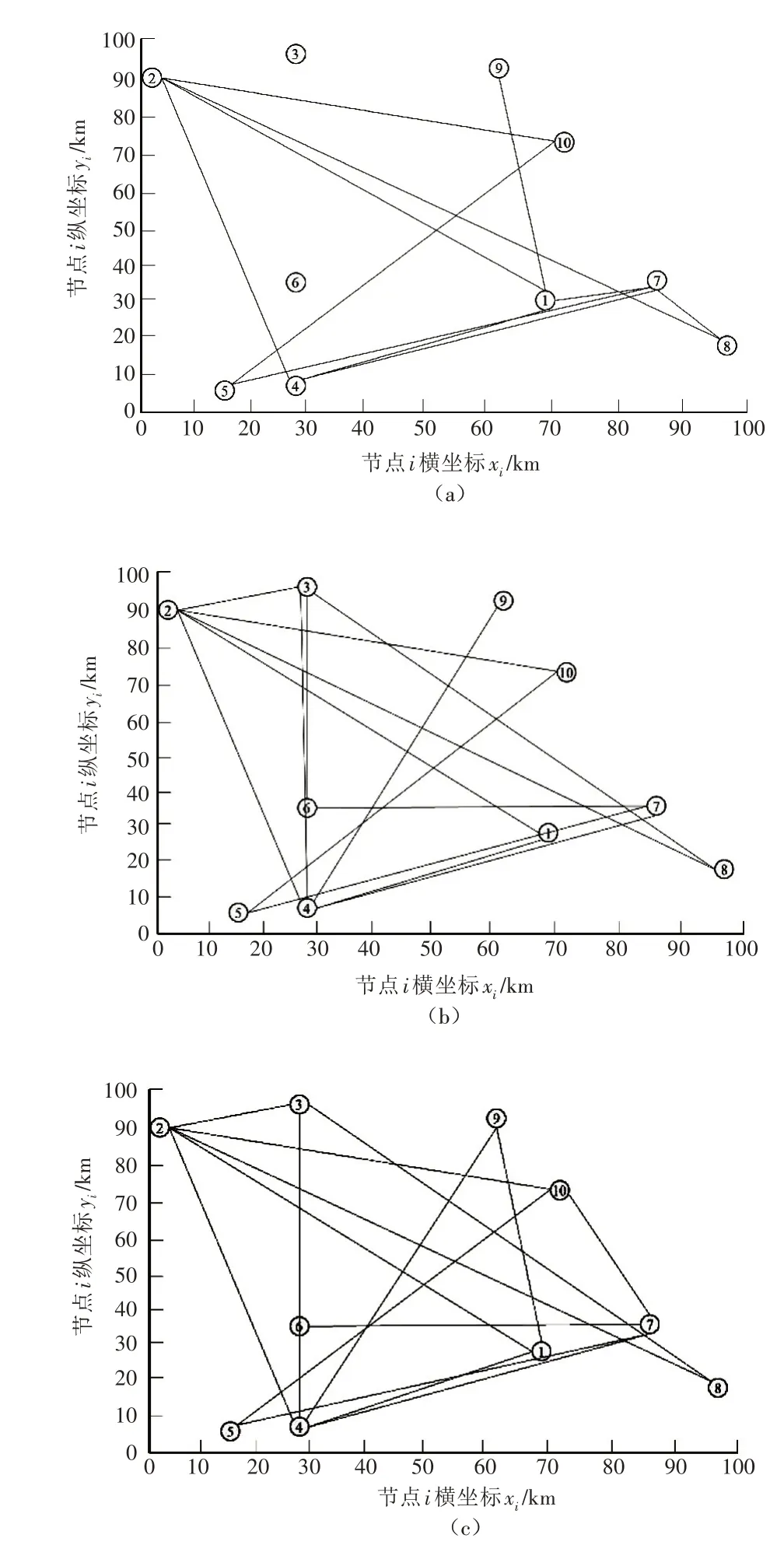
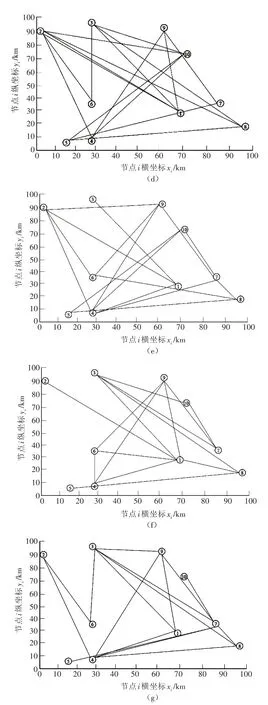
图4 节点连通动态演示图

计算结果表明，两阶段启发式算法能在较短时间内给出较为满意的解，可为规划实践中大规模网络优化问题的求解提供一定的方法借鉴。在公路网布局规划实践中，也可通过该方法获得初始路网，在此基础上，综合考虑自然地形、建设资金、区域发展规划等因素，再结合单因素法、交通区位线法等进行优化调整。

5 结语

交通网络布局是需求到网络形态的映射，而网络的布局形态由节点的连接决定，本文将公路网布局抽象为一定约束条件下节点的连通问题，以路网总旅行时间最小为目标，综合考虑路段重要度和运输需求，构建了公路网布局的混合整数规划模型，以路段重要度和运输需求为启发式条件设计了随机游走算法与模拟退火算法相结合的两阶段启发式算法，通过该两阶段启发式算法可有效求解路网布局问题，获得公路网布局方案。由于在规划实践中影响路网布局的因素较多，本文构建的模型虽能在一定程度上反映路网布局的目标和要求，但未能全面考虑所有相关因素对节点连通的影响，下一阶段可将区域、国家政策等因素量化并纳入模型中，使模型更贴合规划实际；同时，可从保证节点间的多路连通等方面进一步优化设计两阶段启发式算法，增强路网韧性。