基于主成分分析与多分类支持向量机的单沟泥石流危险性预测

刘超 ，乔圣扬

河北地质大学a.城市地质与工程学院b.河北省高校生态环境地质应用技术研发中心，河北石家庄050031

0 引言

泥石流是山区常见的一种地质灾害，严重威胁到了人类的生命与财产安全[1-3]，因此对泥石流开展危险性预测尤为重要。泥石流危险性的预测方法很多，如专家经验法[4]、经验公式计算法[5]、软件模拟法[6]、GIS法[7]等。

近年来，随着机器学习算法热度的逐渐升高，许多学者将机器学习的方法引入到泥石流危险性等级预测中，常见的机器学习方法有随机森林[8]、神经网络[9-11]、支持向量机[12-13]等。刘永垚[14]等（2018）建立基于交叉验证的随机森林模型对泥石流易发性进行评价。张永宏[15]等（2018）使用平均影响值算法筛选主要影响指标，结合神经网络算法预测泥石流易发程度。Qian X[16]等（2016）使用粒子群算法的支持向量机模型对泥石流危险性有较高的辨识精度。Shiuan W[17]等（2009）建立决策树与支持向量机的混合模型对样区发生泥石流的危险性类别进行预测，模型预测准确率为73%。宁志杰与周爱红[18]（2020）提出空间变异性会影响支持向量机模型的适用性，需要合理地选择评价指标。

本文基于白龙江流域泥石流，通过主成分分析（Principle Component Analysis，PCA）提取3个互为独立的主成分，进一步使用5折交叉验证的方式抽取训练样本与预测样本。联合使用多分类支持向量机（Multi-classification Support Vector Machine，MSVM）对泥石流危险性类别进行分类，建立主成分分析与多分类支持向量机预测模型（PCAMSVM），可为预测白龙江流域泥石流危险性提供科学依据。

1 基本理论

1.1 主成分分析

泥石流危险性通常被众多指标所影响，而指标与指标中的信息会存在部分程度的相关性，使各指标间出现信息重叠问题，因此利用主成分分析把存在相关性的指标线性组合后，形成互为独立的新综合指标，从而达到降维目的。具体步骤如下：

（1）标准化原始数据

采集到的数据构成矩阵X，即：

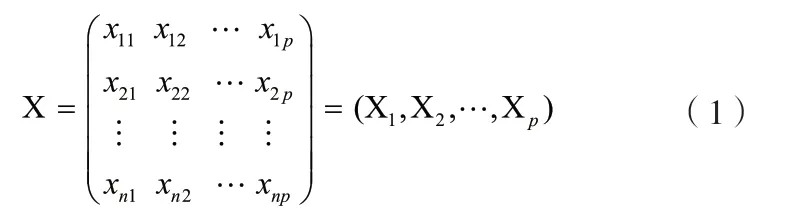
式中，n为样本个数，X1，X2，…，XP为涉及的P个指标。其中：

（2）计算相关系数矩阵

计算X*的相关系数矩阵：

（3）计算特征值与特征向量

计算相关系数矩阵R的p个特征值分别为λ1，λ2，…，λp，以及每个特征值λk（k=1,2,…,p）对应的特征向量为：

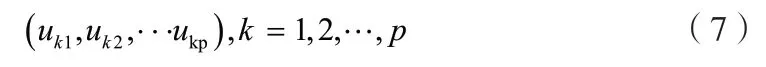
（4）选取主成分

主成分是原始指标的线性组合。通过主成分分析得到p个主成分，前m个主成分的累计方差贡献率为：

在解决实际问题时，累计方差贡献率通常选取大于85%时所确定的前m个主成分。

（5）计算主成分

主成分是通过选择前m个特征值所对应的特征向量来计算的。计算的主成分为：

式中，把Yk称为第k主成分。主成分的线性表达式写为：

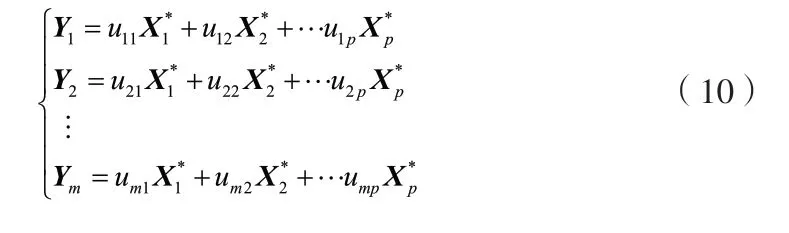
1.2 多分类支持向量机

支持向量机是一种分类方法，常用的解决多分类问题（分类数大于2）的总体思路是把多分类转化为若干个二分类。这样可将具有N个分类的数据模型转化为个二分类模型，即每两个类别之间用二分类方法进行一次分类[19]。

在MSVM中将样本分为训练样本与测试样本。设训练样本为：

其中，xt为p维向量，p为指标数，yt为分类标签，l为样本个数。二分类的具体步骤如下：

（1）构造最优超平面

设二分类模型的两个分类为i和j，构造最优超平面如图1所示：

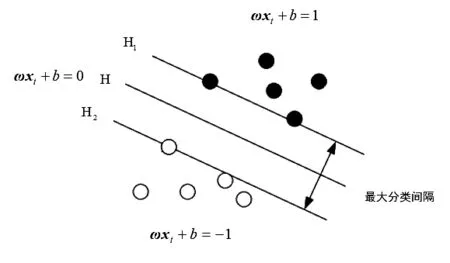
图1 最优超平面示意图Fig.1 Hyperplane diagram of optimal classification

图1中，黑色小球表示分类i的样本（分类标签用1来表示），白色小球表示分类j的样本（分类标签为用-1来表示）。设H为最优超平面，H1、H2分别平行于H，是经过两类样本并且离H最近的面，H1与H2的平分面为H。最大分类间隔是指H1与H2之间的距离。因此H的方程不妨设为：

式中，ω和b为待求解的参数。图1中，H1与H2的方程可以相应的设为：

有时两类样本中个别数据点不能精确地被最优超平面正确划分，则引入松弛项tξ≥0，放宽约束条件，即：

式中，C为惩罚因子，是对错误分类样本增加惩罚因素的参数。

为了求解上述凸二次规划问题，构建拉格朗日函数，并对此函数进行求偏导，再转化为对偶问题进行求解，可求得最优解w*、b*，确定分类函数[20]。对于非线性问题引入核函数，最终得到的分类函数为：

式中，sgn（·）为符号函数，x为预测样本，yt为分类标签，at*为对偶变量最优解，K（xt ,x）为核函数。

（3）判别分类

经过对相邻玻璃折弯角度多次进行计算机三维实体建模及实体渲染。总结出玻璃折弯角度应控制在不小于170°，使玻璃之间光线折射效果可以得到有效的缓解，且观感效果极佳（见图2）。

通过分类函数判断类别，f（x）=1时，判断类别为分类i，f（x）=-1时，判断类别为分类j。对于多分类问题，应用MSVM进行分类，对于每一个样本数据进行CN2次二分类，采用投票法判别最终分类。即在i、j分类时，分类函数判断为i类，就在i类上加一票，判断为j类，在j类加一票，然后进行其他二分类，直到所有分类函数都完成判别后，再判别样本所属分类，样本所属分类是根据最后统计类别票数最多而确定的。

2 预测模型的建立

以白龙江流域泥石流为例[20]，联合使用主成分分析和多分类支持向量机的方法，利用Matlab软件编译程序，进行泥石流危险性预测。

白龙江流域位于青藏高原与四川盆地的过渡区，该地区高差大，纵坡陡峭，山坡坡度较大，降雨具有强度大、历时短、突发性等特点[21]。此流域极易发生泥石流，给当地造成了严重的危害，特别是2010年舟曲发生了特大泥石流灾害，县城几乎被泥石流摧毁殆尽，死亡和失踪人数超过两千余人[3]。

2.1 评价指标确定

以文献[20]中白龙江流域泥石流30组数据为例，选取7个指标作为评价因子,如表1所示。泥石流危险性等级分为四类，低度危险用标签“1”表示、中度危险用标签“2”表示、高度危险用标签“3”表示、极高危险用标签“4”表示[22]。

表1 白龙江流域泥石流原始数据[20]Table 1 Primary data of debris flow in Bailong River basin

2.2 主成分分析提取

对原始数据进行标准化，进一步根据式（6）可得到相关系数矩阵。

式中，相关系数越接近1表明指标与指标之间越相关，表明各指标间存在大量重叠信息。因此通过PCA提取主要信息。

然后计算相关系数矩阵的特征值及相应的贡献率，如表2所示。从表2中可以看出，前3个主成分累计贡献率达到85.512%，因此提取前3个主成分。

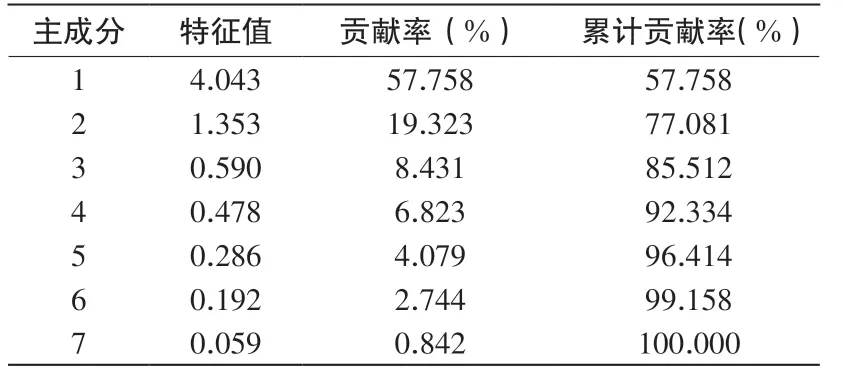
表2 特征值、贡献率及累计贡献率Table 2 Eigenvalue, contribution rate and cumulative contribution rate

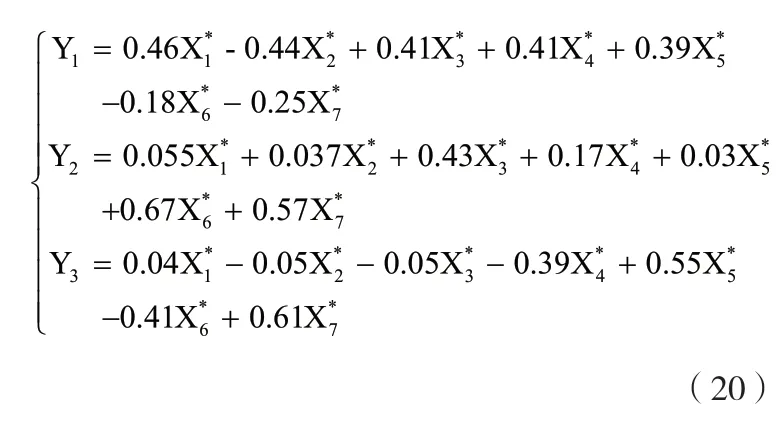
其中，X1*、X2*、X3*、X4*、X5*、X6*、X7*分别表示流域面积、松散固体物质总量、爆发规模、工程治理拦砂量、沟床平均比降、流域切割密度及不稳定沟床比这7个指标标准化之后的数值。主成分的计算结果如表3所示。

表3 主成分的计算结果Table 3 Principal component calculation results

2.3 MSVM模型的建立

MSVM模型选取5折交叉验证方法抽取训练样本与测试样本，再进行MSVM预测。将30个样本按序号等分为5个子集，每个子集6个样本。在每次实验中，按照顺序选择其中1个子集作为预测样本，另外4个子集作为训练样本，进行模型的训练与预测，得到预测的准确率。同样的实验再进行4次，模型准确率取5次预测的准确率平均值。

其具体过程如图2所示。

图2 5折交叉验证示意图Fig.2 5-fold cross validation schematic diagram

MSVM模型中选取高斯核函数，参数寻优算法选取粒子群算法。

2.4 模型预测结果

按照5折交叉验证方法进行PCA-MSVM预测，预测结果如图3和表4所示。由图3可知，在第2次实验、第3次实验以及第5次实验各有1次误判。由表4可知，PCA-MSVM模型准确率达到了90%，能够满足实际工程的需求。

表4 基于交叉验证的PCA-MSVM模型预测结果统计Table 4 Prediction result statistics of PCA-MSVM model based on cross validation

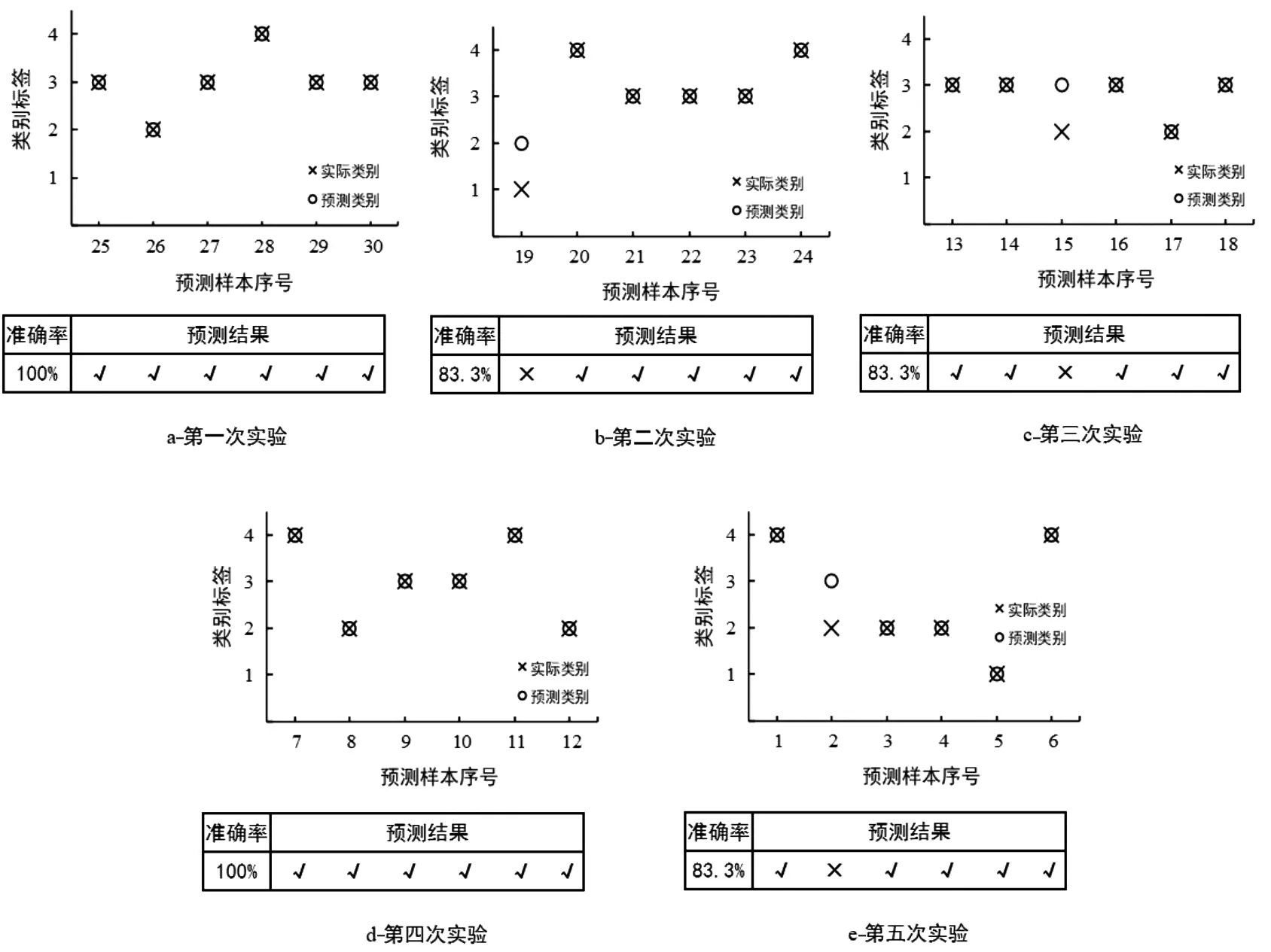
图3 基于5折交叉验证的PCA-MSVM模型预测结果Fig.3 Prediction results of PCA-MSVM model based on 5-fold cross validation

3 讨论

3.1 PCA对MSVM模型准确率的影响

基于白龙江流域泥石流30组数据，对比单独MSVM和PCA-MSVM模型预测的准确率，预测结果如图4所示。

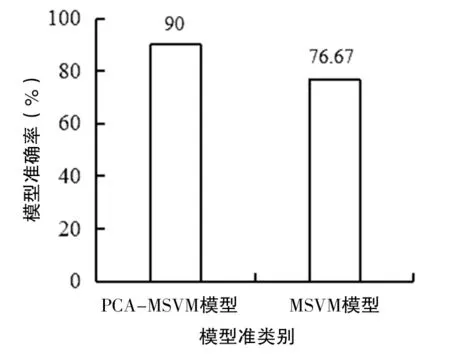
图4 PCA-MSVM模型与MSVM模型预测结果对比Fig.4 Comparison of prediction results between PCAMSVM model and MSVM model

由图4可知，PCA-MSVM模型准确率可达90%，MSVM模型准确率仅为76.67%，PCA-MSVM模型明显优于MSVM模型。在建立MSVM模型之前，对原始数据进行主成分分析，可以去除原始变量之间的相关性，达到一定的降维效果，建立互不相关且保留原有信息的综合指标，可有效提高预测性能。

3.2 交叉验证折数K对模型准确率的影响

在基于PCA-MSVM模型下分析模型预测准确率随K值的变化，如图5所示。

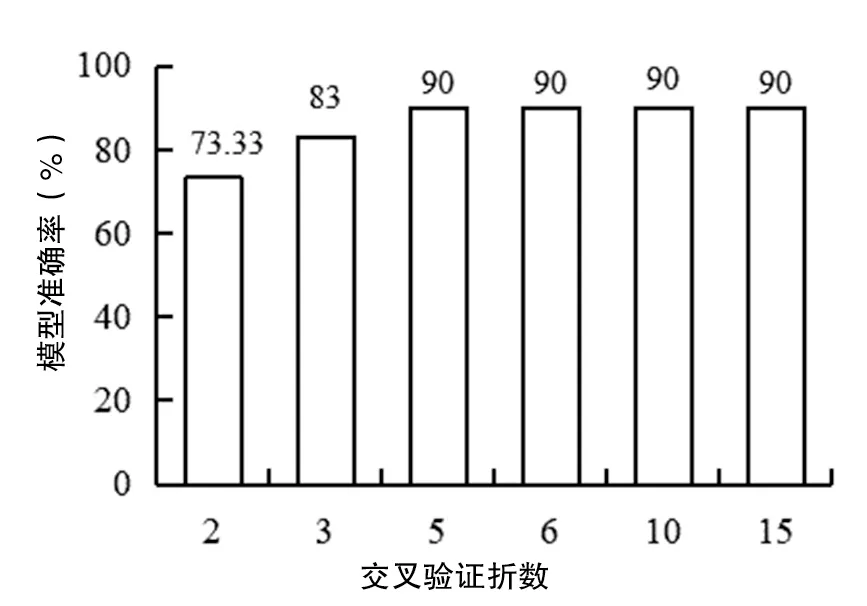
图5 模型准确率随K值的变化Fig.5 Model accuracy varies with K value

由图5可知，模型准确率随着K值增大而增加，当K≥5时，模型准确率可以达到最大值90%。K值较小时，训练样本数量较少，训练出的模型泛化能力较差，导致模型准确率较低。随着K值的增大，模型泛化能力增强，模型准确率也随之提高。K值大于5时，模型准确率随K值增大变化并不明显。K值增大会加大程序运行时间与运算复杂程度，因此上文预测模型中选取了K为5，即5折交叉验证。

4 结论

本文选取白龙江流域泥石流为例，通过主成分分析对原始数据进行处理，提取主成分，基于交叉验证提取训练样本与预测样本，联合多分类支持向量机算法对泥石流危险性进行预测，可以得到以下结论：

（1）PCA-MSVM模型能够很好的预测泥石流危险性，以白龙江流域泥石流30组数据为例，使用5折交叉验证的PCA-MSVM模型进行预测，模型准确率可达90%。

（2）通过MSVM模型与PCA-MSVM模型的对比分析，PCA-MSVM模型准确率较高。引入PCA可以起到降维作用，减少相关性，提高MSVM模型准确率。

（3）模型准确率随交叉验证折数K增大而增加，当K达到某一值后，模型准确率趋于平缓。本文中，K<5时，模型准确率较低，并随着K增大而增加，K≥5时，K值达到最大为90%，趋于稳定。在程序计算过程中，随着K的增大运算时间增加。