热-力耦合作用下花岗岩蠕变损伤模型

刘 凯， 余宏波， 王 焱， 谭维佳

(1.青岛地质工程勘察院(青岛地质勘查开发局)， 青岛 266000; 2.青岛地矿岩土工程有限公司， 青岛 266000； 3.天津大学地球系统科学学院， 天津 300072； 4.长安大学地质工程与测绘学院, 西安 710054)

岩石是一种非性质非均质的复杂地质材料，在外界应力、温度、风化、水等因素的作用下，材料内部损伤不断累积，从而导致宏观力学性能的劣化，对岩体工程施工及运营造成潜在威胁[1-2]。随着地下资源的不断开发利用，地下岩体开挖和地热开发等人类活动愈发频繁，深部岩体处于热-力耦合作用下，蠕变变形效应十分显著，因此研究热-力耦合作用下岩石蠕变力学特性、建立全面可行的本构模型具有十分重要的意义[3-4]。

中外对于温度效应下岩石蠕变本构关系的研究已有部分成果，Miura等[5]提出一种模拟水、温度和应力对岩石蠕变影响的微观力学模型；Günther等[6]探究盐岩稳态蠕变速率与温度及应力之间的联系，构建了不同温度、应力条件下的盐岩蠕变模型；茅献彪等[7]开展高温状态下泥岩单轴蠕变试验，建立了考虑温度影响的泥岩蠕变经验模型；王艳春等[8]提出温度-应力-化学耦合作用的页岩蠕变模型；王春萍等[9]考虑花岗岩流变参数在温度作用下的非定常性，建立考虑温度影响的改进西原模型；李畅等[10]进行红层泥岩高温后蠕变试验，得到温度对蠕变参数的影响规律，从而改进Burgers模型；沈朝辉等[11]建立了花岗岩蠕变参数与温度之间的数学关联，在分数阶蠕变模型的基础上进行改进；王永岩等[12]在传统西原模型的基础上，引入了某个考虑温度、围压影响的损伤变量，得到考虑温度-围压共同作用的西原损伤模型。

花岗岩作为一种高强度、低渗透性的脆性岩石，被认为是高放射性废料处置库的理想围岩，但深部花岗岩在热-力耦合作用下，蠕变变形较明显[13]，因此研究花岗岩在温度效应和荷载时间下的蠕变本构关系具有重要意义。现基于三峡细粒花岗岩20～300 ℃蠕变试验，分析瞬时应变、蠕变应变率与温度之间的关系，定义瞬时、蠕变热损伤变量。采用Heard指数型模型描述花岗岩稳态蠕变行为，构建广义Kelvin热损伤模型和黏塑性热损伤元件，串联后得到一个新的热-力耦合作用下的花岗岩蠕变损伤模型。给出模型参数求解方法，分析瞬时、蠕变热损伤变量变化规律，辨识三种花岗岩的蠕变试验数据验证所建模型的合理性和适用性。以期为热-力耦合作用下花岗岩蠕变行为模拟及深部地下工程、高放射性废料处置工程长期稳定性研究提供一定参考。

1 花岗岩蠕变试验

1.1 试验概况

刘泉声等[14]开展不同温度下花岗岩单轴压缩蠕变试验。花岗岩试样采自长江三峡坝区，呈灰黑色，细粒结构，主要成分有石英、长石、角闪石、黑云母及少量胶结物。将新鲜岩样运回试验室加工成直径为50 mm，高度为100 mm的圆柱体，应力加载前，首先以2 ℃/min的速率提至目标温度，再保持目标温度4 h后施加恒定轴向荷载。温度条件分为20、60、80、100、200和300 ℃，轴向应力均为120 MPa，蠕变试验曲线如图1所示，其中20 ℃和100 ℃试验时间分别为8 300 h和4 200 h，其余温度条件下的试验时间约为700 h，为便于对比观察，图1时间轴最大值设为2 000 h。

图1 不同温度下花岗岩蠕变曲线

从图1可看出，花岗岩在加载瞬间表现出瞬时弹性变形，接着进入衰减蠕变阶段，该阶段岩石应变率递减，当应变率递减到一定程度时，岩石进入稳定蠕变阶段，此时应变率保持基本稳定。当温度T=300 ℃ 时，花岗岩还表现出一定的加速蠕变行为。

1.2 结果分析

图2为不同温度下花岗岩的瞬时应变曲线，图3为不同温度下花岗岩蠕变应变率曲线，为使得应变率数据点对比更加直观，时间横轴最大值设为650 h。

图3 不同温度下蠕变应变率随时间变化曲线

由图2可看出，花岗岩在处于同一应力条件时，随着温度的提升，瞬时应变值近线性递增。由于瞬时弹性模量与瞬时应变呈反比，可发现花岗岩瞬时弹性模量随着温度提升而呈递减趋势，温度的升高导致花岗岩瞬时弹性模量发生瞬时损伤。

图2 不同温度下花岗岩的瞬时应变曲线

由图3可看出，在同一温度条件下，花岗岩蠕变应变率先递减，接着在某一恒定水平附近波动，这反映出衰减蠕变到稳定蠕变的流变过程。花岗岩稳态蠕变速率大致随着温度提升而呈递增趋势，这体现出了温度升高对蠕变损伤发展的促进作用。

综合图2、图3可发现，温度对花岗岩瞬时弹性模量造成瞬时损伤并促进花岗岩后续蠕变损伤过程。

2 热-力耦合作用下花岗岩蠕变损伤模型

2.1 模型结构建立

岩石是一种同时包含弹性、黏弹性、黏性和黏塑性变形行为的复杂材料[1]，蠕变本构模型需同时考虑弹性、黏弹性、黏性和黏塑性应变。Cvisc模型(图4)是一种元件模型，包含弹性体、Kelvin体、牛顿体和黏塑性元件，分别对应图4模型中的第1、2、3、4部分，鉴于Cvisc模型结构简练且可同时描述岩石黏弹塑性变形，故在Cvisc模型的基础上进行改进，以期得到能反映温度效应的花岗岩蠕变本构模型。

E1为第1部分的瞬时弹性模量；E2和η2分别为第2部分的弹性模量和黏性系数；η3为第3部分的黏性系数；η4为第4部分的黏性系数；σ为应力；σS为长期强度

根据岩石黏弹塑性应变特点，结合图4中模型结构，得到岩石应变方程：

ε=ε1+ε2+ε3+ε4

(1)

式(1)中：ε1、ε2、ε3和ε4分别对应图4模型中的第1、2、3、4部分的应变；ε为模型总应变。

单轴条件下，Cvisc模型本构方程[2]为

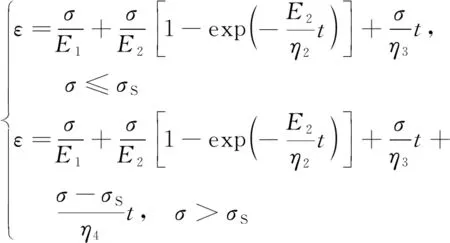
(2)

式(2)中：t为时间。

2.2 Heard稳态蠕变模型

为研究花岗岩稳态蠕变速率随温度的变化规律，选择图3中T=300 ℃下51 h51 h的蠕变速率点，取平均值后得到花岗岩稳态蠕变速率随温度的变化曲线，如图5所示。

图5 稳态蠕变速率随温度的变化曲线

由图5可看出，稳态蠕变速率与温度呈指数函数递增规律。Heard模型[15]是一种反映岩石稳态蠕变速率随温度变化规律的指数型本构模型，鉴于该模型能从某种意义上表征稳态蠕变速率随温度的指数函数变化规律，本文引入Heard模型，其应变率本构方程为

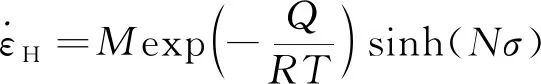
(3)

式(3)中：εH为稳态蠕变速率；Q为激活能；R为摩尔气体常量；R=8.314 J/(mol·K)；σ为应力；T为热力学温度；M和N为流变常数。

由于岩石稳定蠕变阶段以黏性变形为主[3]，故利用Heard模型替换Cvisc模型第3部分牛顿体，对式(3)进行积分得到ε3为

(4)

式(4)即为Heard稳态蠕变模型本构方程。

2.3 损伤变量的定义

由于温度同时影响花岗岩的瞬时损伤和蠕变损伤，分别建立瞬时、蠕变热损伤变量来描述花岗岩损伤发展过程。

(1)瞬时热损伤变量D1。依据损伤力学理论，参考文献[16]，定义瞬时热损伤变量D1为

(5)

式(5)中：E(T)为不同温度下的瞬时弹性模量；E0为常温下的瞬时弹性模量。

(2)蠕变热损伤变量D2。定义蠕变热损伤变量时，本研究以某一恒定应力或恒定温度条件为前提，考虑温度对蠕变热损伤相关参数的影响。卡恰诺夫[17]认为在一维应力状态下，蠕变条件下的损伤发展方程为

(6)

式(6)中：D2为蠕变热损伤变量；A和ν为与温度、应力有关材料参数。

积分式(6)得到蠕变损伤破坏时间te为

te=[A(ν+1)σν]-1

(7)

联立式(6)和式(7)可得蠕变热损伤变量D2的演化规律：

(8)

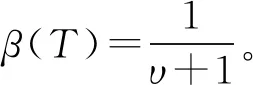
图6 不同β值下D2与的关系曲线

由图6可看出，β值越小，D2接近1时的损伤曲线斜率越高，对应岩石加速蠕变阶段速率越高，此时岩石趋于表现出脆性破坏特征；相反地，β值越大，D2接近1时的损伤曲线斜率越小，对应岩石加速蠕变阶段速率越低，此时岩石趋于表现出延性破坏特征，由此认为β可从一定程度上反映岩石蠕变破坏特征。

2.4 热损伤演化

传统Cvisc模型中第1、2部分分别为弹性体和Kelvin体，分别可描述岩石瞬时弹性和衰减蠕变行为，两者串联后即为广义Kelvin模型。依据Lemaitre[18]效应变原理，分别通过瞬时热损伤变量D1和蠕变热损伤变量D2对Cvisc模型中第1、2部分进行损伤演化，得到广义Kelvin热损伤模型本构关系为

(9)

式(9)即为广义Kelvin热损伤模型本构方程。

当岩石应力超过长期强度后，Cvisc模型第4部分发挥作用，对其损伤演化后得到黏塑性热损伤元件本构关系为

(10)

式(10)即为黏塑性热损伤元件本构方程。

由于Heard稳态蠕变模型本构方程中无弹性模量和黏性系数，且模型已包含了稳态蠕变速率随温度的变化规律，故无需对Heard稳态蠕变模型进行损伤演化。

2.5 热-力耦合作用下的花岗岩蠕变损伤模型

将Heard稳态蠕变模型、广义Kelvin热损伤模型和黏塑性热损伤元件串联，参考Cvisc模型组合方式，得到新的考虑温度影响的花岗岩蠕变本构模型，其本构方程为

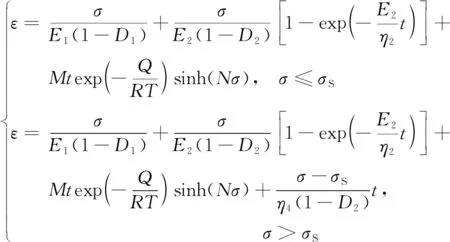
(11)

式(11)即为本文热-力耦合作用下的花岗岩蠕变损伤模型。

3 模型分析验证及参数求解

3.1 参数求取

3.1.1E1和D1

首先确定瞬时热损伤变量D1，假设常温20 ℃下的D1为0，岩石处于无损状态，根据图2中不同温度下的瞬时应变，基于Hooke定律得到不同温度下的瞬时弹性模量E1，从而确定D1，不同温度下的E1和D1如表1和图7所示。

表1 不同温度下的E1和D1

图7 D1随温度变化曲线

根据表1和图7可看出，瞬时热损伤变量D1随温度升高而呈线性递增趋势，D1的数学表达式为

D1(T)=0.000 9T+0.002 9

(12)

在式(12)中，当D1=1时，T=1 108 ℃。说明花岗岩在1 108 ℃下，达到瞬时完全损伤。徐小丽等[19]研究发现花岗岩在超过1 200 ℃的环境下，基本失去承载能力，此时花岗岩在外界瞬时荷载下便会瞬时破坏，由此可认为此时花岗岩在受力瞬间的瞬时热损伤变量D1为1，这与本文结论基本吻合，体现了式(12)的可行性。

3.1.2 Heard稳态蠕变模型参数

图5反映了花岗岩稳态蠕变速率随温度的指数型变化规律，利用式(3)拟合图5中的稳态蠕变速率点，可得Heard稳态蠕变模型参数如表2所示。

表2 Heard稳态蠕变模型参数

3.1.3 其余模型参数

参数E1、D1、M、Q、N通过试验结果已确定，剩余参数为E2、η2、η4、te与β。将不同温度下已求取的参数E1、D1、M、Q、N代入式(11)，通过Origin软件基于Levenberg-Marquardt算法求解E2、η2、η4、te与β，计算结果如表3所示。

表3 模型参数

3.2 模型拟合及蠕变热损伤分析

为了验证本研究所建模型的辨识效果，根据已求解参数代入式(11)得到理论值，与图1中三峡细粒花岗岩单轴压缩蠕变试验数据进行比较，得到理论值与试验值对比曲线，如图8所示。

由图8可看出，本文所建模型拟合精度较高，平均R2为0.990 3，能较为精准识别不同温度下花岗岩蠕变曲线。

图8 拟合值与试验值对比曲线

参数te关系到岩石蠕变损伤破坏时长，β可从一定程度上反映岩石蠕变破坏特征，为研究te、β随温度变化的规律，根据表3得到te、β与温度的关系曲线，如图9所示。

图9 参数te、β与温度的关系曲线

由图9可看出，随着温度的提升，花岗岩的蠕变损伤破坏时间te递减，β值递增。结合2.3节中的分析，可认为花岗岩在温度逐渐提升的过程中，加速蠕变阶段的损伤破坏特性逐渐从脆性向延性过渡转变。te、β与温度之间的经验表达式为

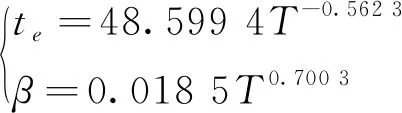
(13)

将式(13)代入式(8)即可得D2的经验表达式，由此得到可同时反映随温度、荷载时间变化规律的蠕变热损伤演化方程，基于此方程取不同温度、时间点进行计算，得到蠕变热损伤变量D2与温度、时间的三维关系，如图10所示。

图10 蠕变热损伤变量与温度、时间的三维关系图

由图10可看出，当岩石保持在同一温度下，蠕变热损伤变量D2随着荷载时间增长而不断累积。当岩石处于同一时刻，D2随着温度提升而逐渐增大。当T=1 200 ℃，t=900 h时，D2=1；当T=1 000 ℃，t=1 000 h时，D2=1，这说明了岩石蠕变热损伤的累积同时受温度和荷载时间的影响，温度和荷载时间均促进蠕变损伤发展，温度越高，岩石蠕变热损伤累积越快。

3.3 模型适用性验证

本文中的模型基于不同温度的花岗岩蠕变试验而建，然而某一实际工程中花岗岩多处于温差不大的应力环境中，故还需通过同一温度下不同加载应力的花岗岩蠕变试验数据拟合来验证模型适用性。引用文献[20-21]中辽宁高德地区细粒花岗岩和新疆塔什库尔地区中粒花岗岩相关蠕变试验数据，依据本文所建模型及参数解析方法进行拟合解析，得到拟合值与试验值对比曲线，如图11所示。

图11 拟合值与试验值对比曲线

由图11可看出，本文中所建模型识别效果较好，拟合精度较高，平均R2分别为0.990 7和0.986 5，能较为准确地描述花岗岩在不同温度环境下的蠕变特性，这说明本研究所建蠕变模型对于热-力耦合作用下的花岗岩具有一定适用性。

4 结论

(1)温度效应下，花岗岩的热损伤主要体现在两个方面，一是温度提升导致岩石发生瞬时热损伤，二是温度提升使后续蠕变热损伤不断累积。

(2)花岗岩稳态蠕变速率与温度呈指数递增规律，采用Heard指数型模型描述花岗岩稳态蠕变行为。定义瞬时、蠕变热损伤变量，构建广义Kelvin热损伤模型和黏塑性热损伤元件。参考Cvisc模型结构，得到一个新的热-力耦合作用下的花岗岩蠕变损伤模型。给出参数解析方法，利用三峡细粒、高德细粒和塔什库尔中粒花岗岩蠕变试验数据验证模型合理性和适用性。

(3)β越小，岩石加速蠕变阶段趋于表现出脆性破坏特征；β越大，岩石加速蠕变阶段趋于表现出延性破坏特征。随着温度的提升，花岗岩的蠕变损伤破坏时间te递减，β递增，加速蠕变阶段的损伤破坏特性逐渐从脆性向延性过渡转变。