考虑转动阻抗对砂力学特性影响的离散元分析

王 壮， 段志波， 廖新超， 刘一鸣

(湖北工业大学土木建筑与环境学院， 武汉 430068)

离散单元法由Cundall等[1]于1979年提出，是一种从细观出发研究物质宏观力学特性的方法，被广泛应用于砂土方面的研究。基于离散元法，程升等[2]通过双轴压缩模拟试验，对南海软黏土的细观参数进行了标定；史乃伟等[3]研究了临界状态下砂颗粒的运动状态；蒋明镜等[4]通过单粒组密砂的直剪模拟，分析了剪切带形成的微观机制。

传统的离散单元模拟在生成大量颗粒来确保数值模型具有代表性的同时，为提高其模拟效率，将砂颗粒简化为球形颗粒。颗粒之间的接触作用常被认为仅发生在一个点上，主要由颗粒重叠产生的正向力和由颗粒之间相对滑动产生的切向力组成，忽略了颗粒转动的影响[5]。这导致了颗粒尺度细节的损失，使颗粒集合体材料的剪切强度低于实际值。1982年Oda等[6]通过对椭圆颗粒进行双轴压缩试验发现决定颗粒材料力学机制及微观变形机制的主要因素为颗粒之间相对转动作用。众多学者为考虑颗粒间转动的影响对离散元法进行了改良，并引入转动阻抗的概念[6-9]。Iwashita等[7]进一步拓展了离散元接触模型，在其基础上计入转动分量。Jiang等[8]提出了能完整反映无黏性材料力学行为的抗转动线性接触模型，设定颗粒间的接触为面接触，并考虑了转动阻抗的影响。Jiang等[9]研究表明，将接触力矩纳入离散单元接触模型可以有效地获得更真实的体积强度，并识别颗粒材料的变形行为。Zhao等[10]综合比较了滚动阻力和颗粒形状对颗粒材料内部剪切诱发的织构变化和各向异性的影响，发现滚动阻力模型可有效再现砂土中剪切诱导各向异性的主要特征。转动阻抗的作用不可忽视且与砂土的强度以及变形有着密切联系。

基于上述分析，针对转动阻抗对砂土强度影响的研究已取得了一定的成果，然而在转动阻抗微观影响机理方面研究较少，同时二维研究导致颗粒细节缺失。鉴于此，基于离散元法，通过颗粒流程序PFC3D5.0，采用不同抗转动系数和不同围压进行三轴模拟试验，分析转动阻抗对砂土强度和变形的影响，分别从平均配位数、概率密度函数、颗粒间法向接触力和各向异性的角度分析转动阻抗的细观影响机制。以期为考虑转动阻抗因素的岩土类材料离散单元建模提供理论参考。

1 离散单元模型

1.1 本构模型

本构模型的选取对于数值模拟的准确性至关重要。本文研究采用了两种本构模型，砂颗粒与墙之间的接触为线性接触模型，砂颗粒与砂颗粒间的接触为抗转动线性接触模型，其原理如图1所示。

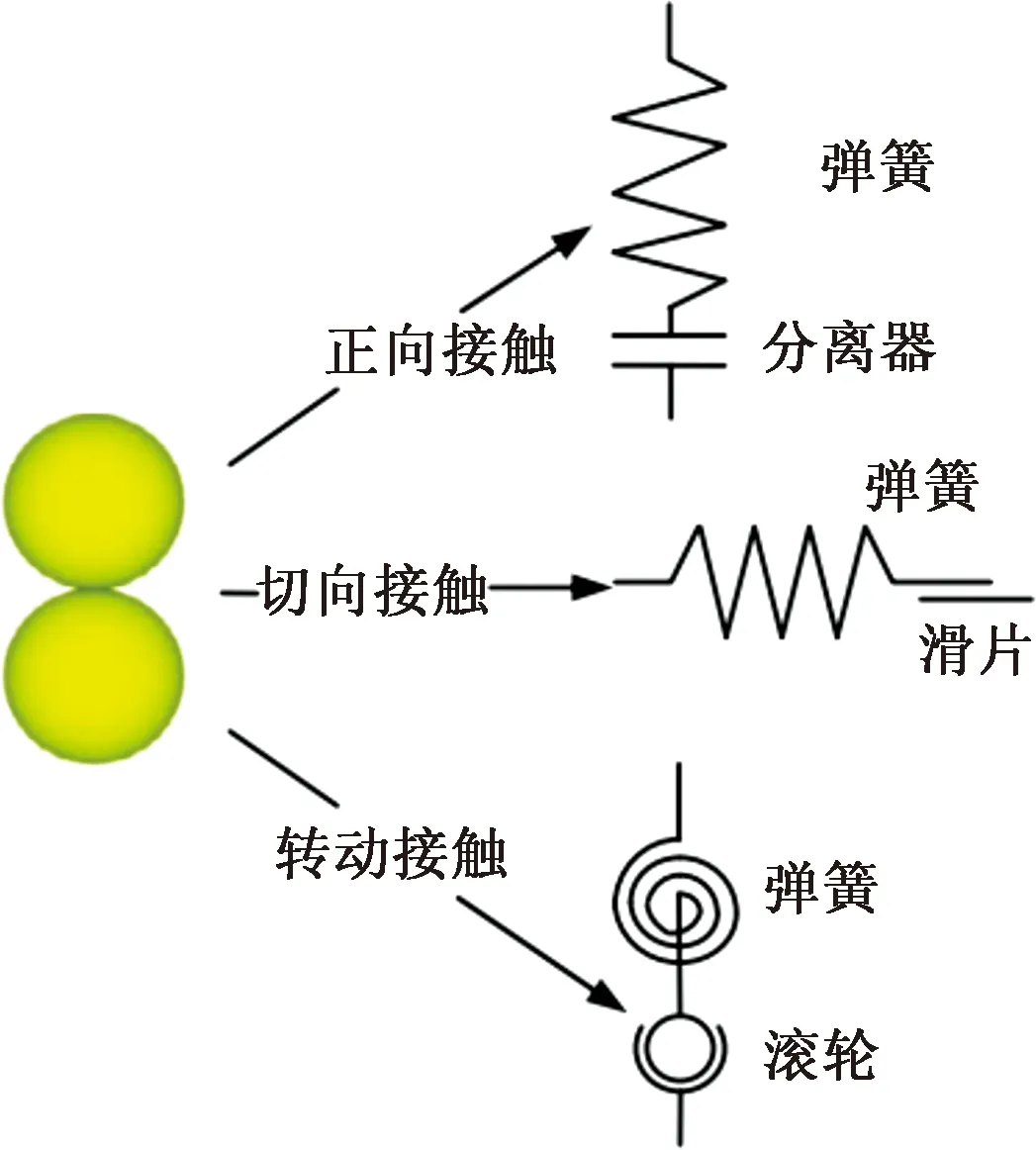
图1 接触模型[3]

线性模型的接触点可以想象为一对弹性弹簧，线性力由具有恒定法向刚度和切向刚度的线性弹簧产生，其力学原理为

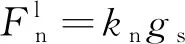
(1)

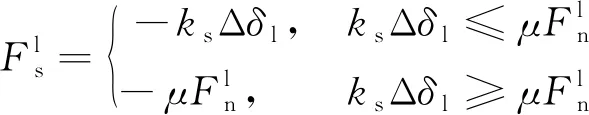
(2)

在线性模型的基础上，抗转动线性接触模型增加了转动阻抗力矩[7]，其定义为

Mr=krθ

(3)

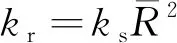
(4)

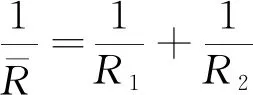
(5)

颗粒转动控制方程为

(6)

内部力矩随着接触点处接触件的累积相对旋转而线性增加。这种累积的最大极限值等于当前法向力与抗转动系数和有效接触半径的乘积。

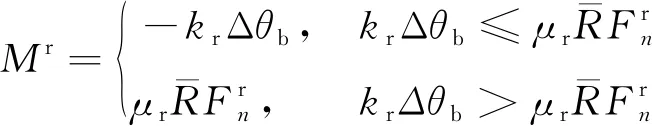
(7)

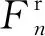
1.2 数值模型

砂真三轴数值模拟试验主要包括以下3个阶段：①制样阶段，首先生成六面无摩擦刚性墙体，形成40 mm×40 mm×80 mm的长方体，然后在长方体内按孔隙率0.35生成颗粒，不平衡力比达到10-5时停止，以平衡制样产生的初始内力；②固结阶段，通过伺服程序控制六面无摩擦刚性墙体的相对移动，施加固结所需的目标围压；③剪切阶段，在伺服机制保持一定围压的同时，通过控制上下两面墙体的相对移动实现对试样的剪切。

模拟试验方案：砂试样建模完成后控制变量，分别取围压为100、200、300 kPa，抗转动系数取0、0.1、0.2、0.3和0.4，共计15组试样，进行固结排水三轴剪切模拟试验。数值模型如图2所示，细观参数的选取如表1所示。

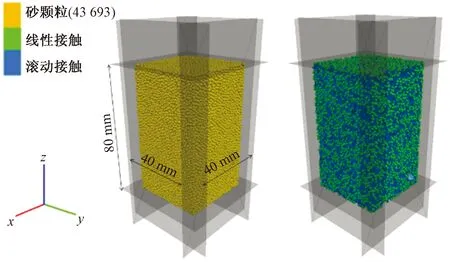
图2 砂真三轴数值模型

表1 数值模拟试验参数

2 宏观结果分析

图3为围压σc=100 kPa条件下，不同抗转动系数时偏应力-轴向应变曲线，各曲线初始阶段基本呈直线且斜率一致，表明转动阻抗对试样初始弹性模量影响不大；随着剪切进一步进行，偏应力相继达到峰值，这是由于转动阻抗抑制了砂颗粒间相对转动，从而破坏面延后出现；达到峰值后，各曲线均表现出软化现象，且抗转动系数越大，软化越明显。

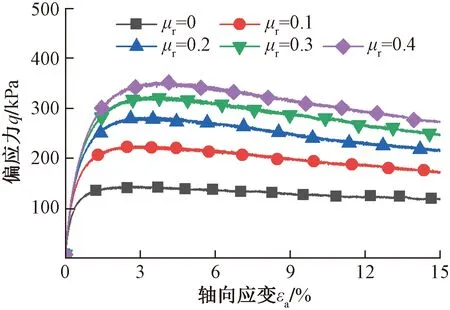
图3 偏应力随轴向应变变化曲线

图4为偏应力峰值随抗转动系数变化曲线，可以看出：抗转动系数和围压的增大，都会引起偏应力峰值增大；其中偏应力峰值增幅随着抗转动系数的增大而逐渐减小，表明转动阻抗的影响逐渐趋于饱和。

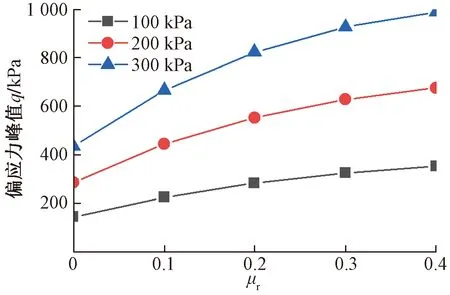
图4 偏应力峰值随抗转动系数变化曲线

图5为100 kPa围压时体应变变化曲线，表现为先剪缩后剪涨，且转动阻抗对剪胀现象有明显增强作用。

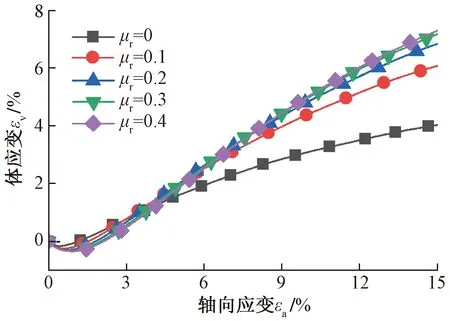
图5 体应变随轴向应变变化曲线

内摩擦角是衡量颗粒材料抗剪强度的重要指标[11]，采用峰值内摩擦角φs来衡量砂的强度，其定义为

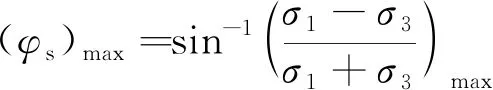
(8)

式(8)中：σ1为大主应力；σ3为小主应力。

由图6可知，试样峰值内摩擦角均随着抗转动系数的增大而增大，且增长幅度逐渐减小，与蒋明镜等[12]研究结果一致。

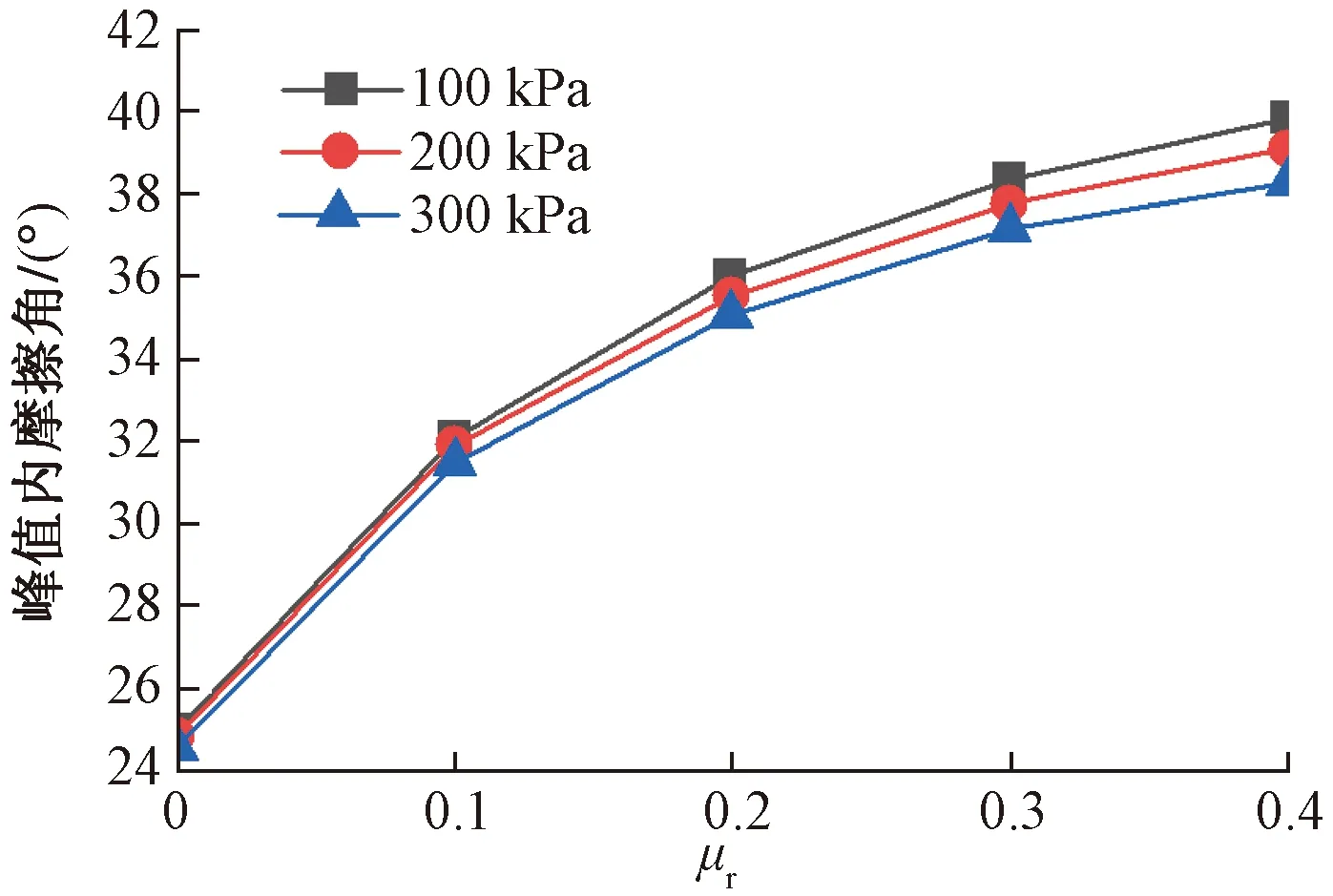
图6 峰值内摩擦角随抗转动系数变化曲线

综上所述，转动阻抗可以有效地提高试样的剪切强度，弥补传统模拟试验中将砂颗粒模拟为球体而导致抗剪强度低于实际值的缺陷。

3 细观力学特性

3.1 力学配位数

配位数是试样中某个颗粒与周围颗粒的激活接触数目，即法向接触力大于零的接触，是判断颗粒材料内部稳定性的重要指标。一般采用平均配位数表征颗粒集合体材料内部颗粒的接触状态。本研究选用平均力学配位数[13]，其定义为

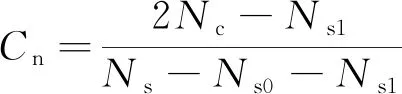
其次，合同文本的语句具有如下特征：第一，多用复杂长句以使语义表达更完整。第二，多用陈述句，因为陈述句可以更好地规定和说明商务合同双方的责任和权利，避免歧义。第三，多使用被动语态，因为合同内容避免掺杂个人感情，被动语态能更客观公正的表达。

(9)

式(9)中：Nc为试样内部总接触数：Ns为试样内部总颗粒数；Ns0为某颗粒周围无接触的颗粒数；Ns1为某颗粒周围接触数目为1的颗粒数。

图7为不同抗转动系数下平均力学配位数随轴向应变的变化曲线，曲线均呈现先微弱增加后下降至某一稳定值趋势。图7中配位数增加是由于试样内部孔隙的压缩，有效接触变多；随着剪切进一步进行，试样发生剪胀，因此配位数降低；最终趋于稳定表明砂粒间形成了稳定的力链结构，有效接触不再改变。抗转动系数越大，曲线出现拐点时的轴向应变越大，且配位数的稳定值越小，这是由于转动阻抗抑制了颗粒间的相对转动，进而延后了稳定力链结构的形成，且减小了平均配位数。围压对于配位数的影响符合一般规律，围压越大，配位数越大。

图7 配位数随轴向应变变化曲线

3.2 概率密度

法向接触力可以用概率密度函数(probability density function，PDF)进行统计量化。Azéma等[14]根据平均法向接触力〈fn〉，将法向接触力fn分为强、弱接触力。对应的接触力分别随归一法向接触力fn/〈fn〉呈指数分布和近乎幂函数分布状态，其表达形式为

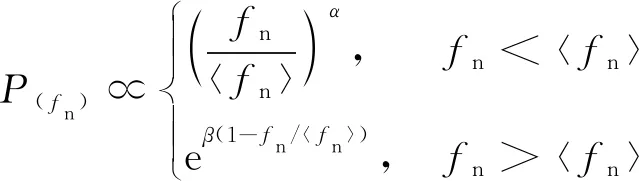
(10)

式(10)中：α、β为拟合参数。

图8反映了σc=100 kPa时峰值状态下，转动阻抗对法向接触力概率密度分布的影响规律，从图8(a)可知，不同抗转动系数条件下概率密度均随着法向接触力的增大而减小，当法向接触力较小时，转动阻抗对其概率密度影响不明显；而较大的法向接触力的概率密度随着抗转动系数的增大而增大。

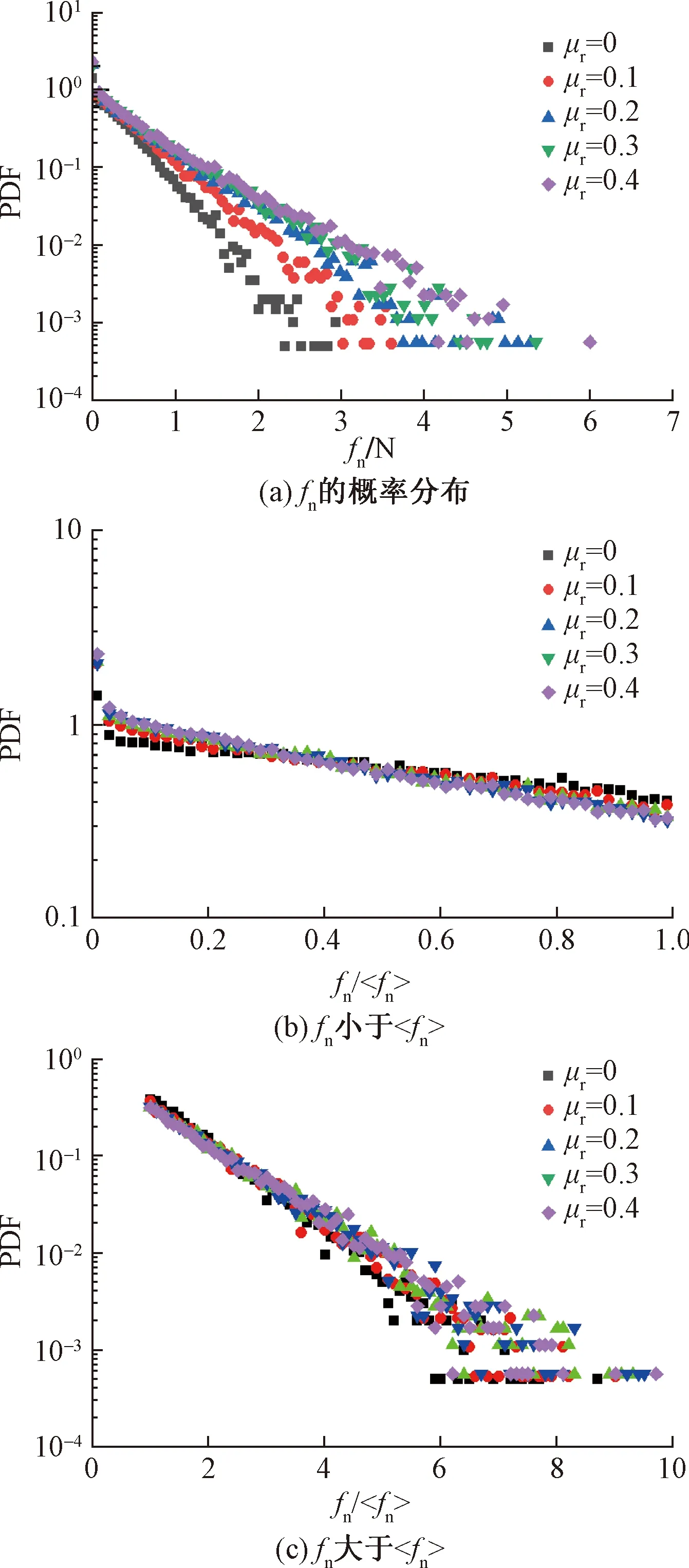
图8 法向接触力概率密度分布

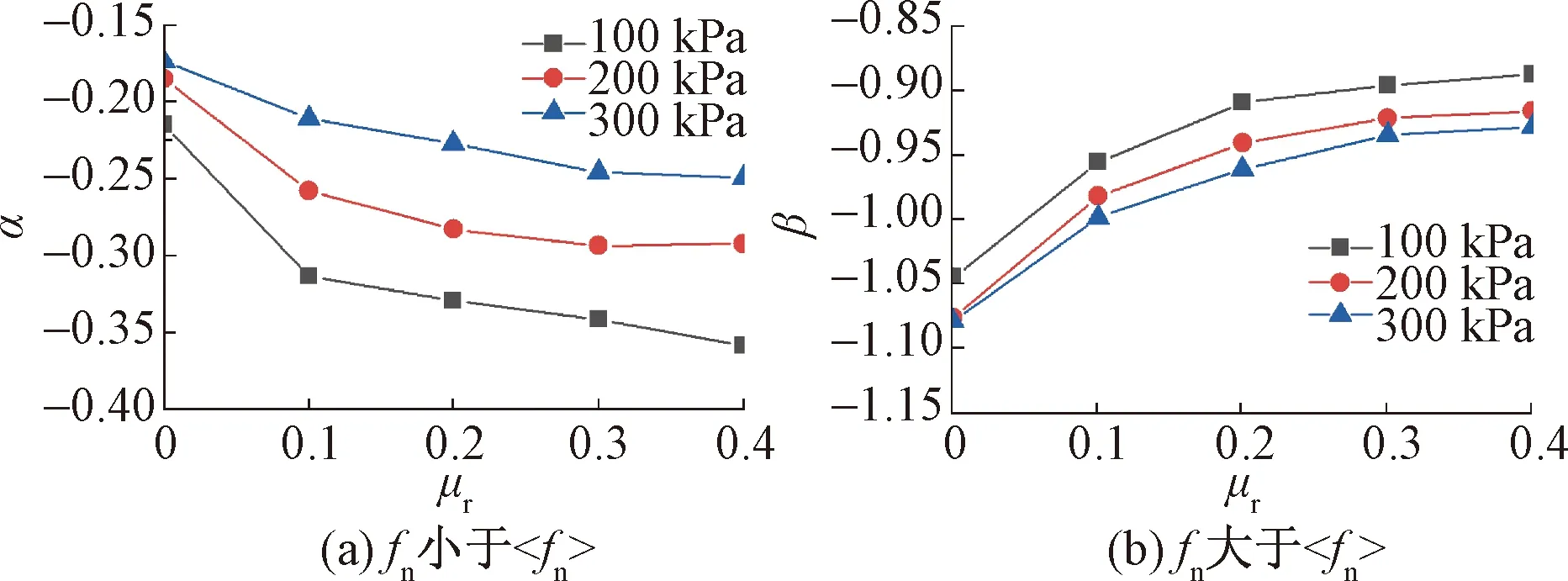
图9 不同抗转动系数对应的拟合参数

3.3 法向接触力

图10为峰值状态下平均法向接触力随抗转动系数的演化曲线，由图10可知，平均法向接触力随抗转动系数增加呈增长趋势，且围压越大，增长趋势越明显。

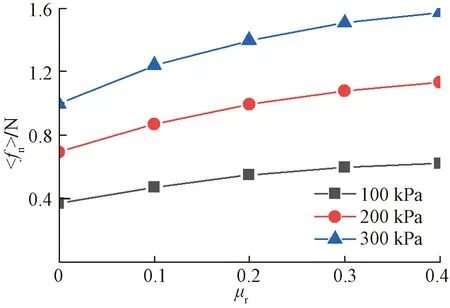
图10 平均法向接触力随抗转动系数变化曲线

法向接触力的空间分布可以采用三维球面直方图[15]直观描绘。图11中每一根棱条表示在其方向上的归一化局部平均法向接触力

图11为100 kPa围压时各特征状态下的三维直方图，直观反映了局部平均接触力分别在初始状态、峰值状态和最终状态的空间分布情况。初始状态时，三维直方图均近似球体，即法向接触力基本表现为各向同性；峰值状态时，球面直方图沿竖向拉长，表示加载方向形成强接触力，而随着抗转动系数的增大，球面直方图更加细长，其尺度范围随之增大，表明抗转动阻抗增大会增强其各向异性程度，使强接触力抵抗轴向加载的能力更强；相比于峰值状态，最终状态较为粗短，即其各向异性在峰后呈现近似软化趋势。

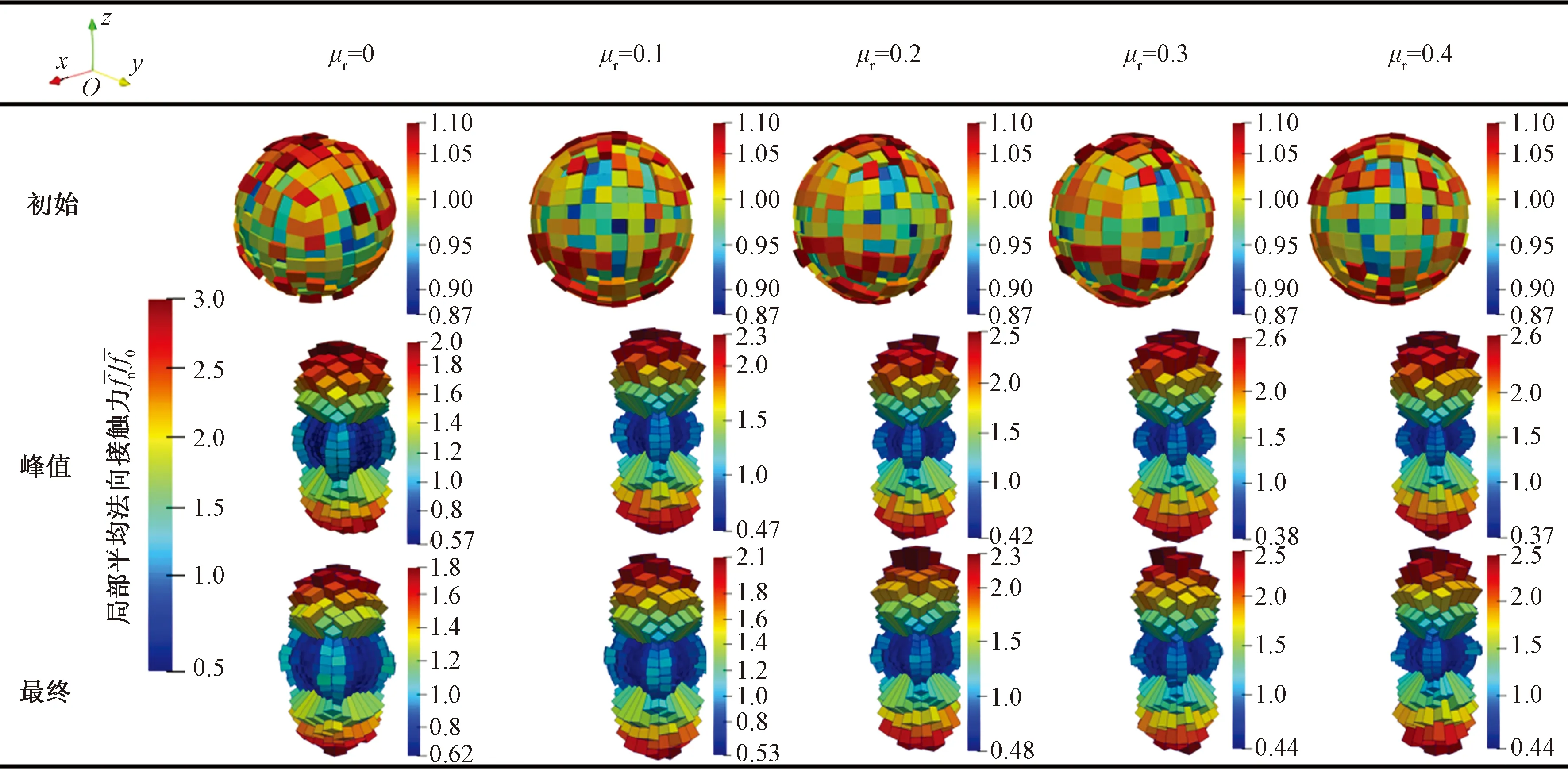
图11 局部平均法向接触力三维演化

3.4 各向异性

剪切导致砂颗粒间接触状态不断变化，砂颗粒间的接触重分布进而导致组构各向异性的演化。Oda[16]结合结构各向异性与排列密度定义了组构张量，通过分布密度函数E(Ω)和接触法向各向异性系数ac来表征组构张量。

(11)

(12)

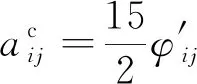
(13)

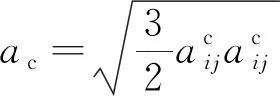
(14)

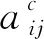
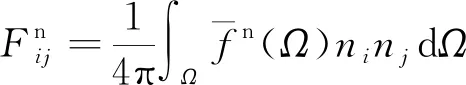
(15)

(16)

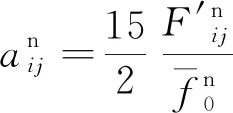
(17)

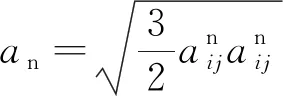
(18)

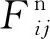
图12和图13分别为不同围压条件下，接触法向各向异性系数(ac)和法向接触力各向异性系数(an)随轴向应变的变化曲线。剪切前期，由于试样发生膨胀变形，ac和an的演化规律十分相似，均表现为急剧增加；达到峰值后，ac趋于稳定，这是由于试样演化出的接触法向各向异性程度达到上限，即试样内部已经形成较为稳定的接触结构，这与配位数最终趋于稳定相互匹配；而an随剪切进一步进行显示出软化趋势，且抗转动系数越大，软化趋势越明显，与应力应变规律相对应，表明法向接触力对抗剪强度具有显著的贡献。对比图12与图13可知，整个剪切过程中，an均大于ac，这是由于法向接触力大小的非均匀分布导致的。随着抗转动系数的增大，ac与an均随之增大，且两曲线拐点对应的轴向应变亦随之增大，表明转动阻抗增大了剪切诱导各向异性的演化程度，进而提高了砂的抗剪强度及稳定性。

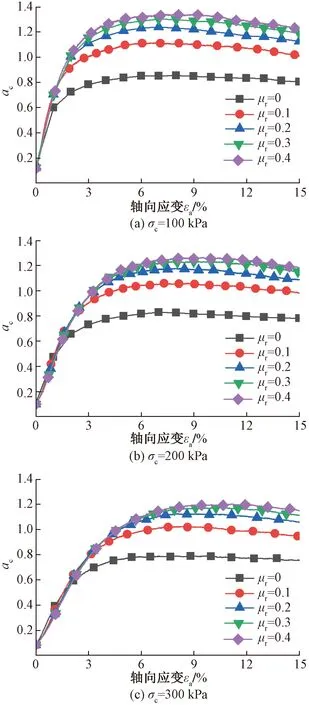
图12 接触法向各向异性系数随轴向应变变化曲线

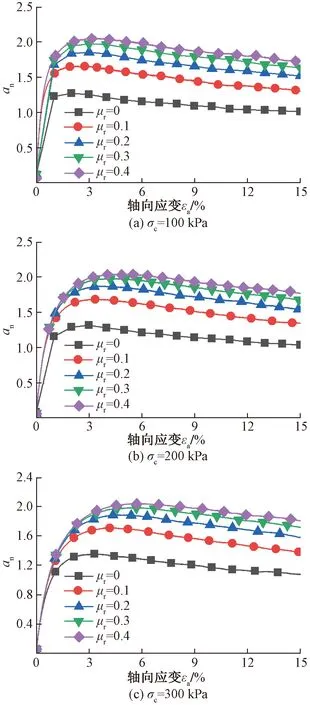
图13 法向接触力各向异性系数随轴向应变变化曲线

4 结论

(1)转动阻抗对砂体强度及变形规律存在显著的影响，随着抗转动系数增大，峰值强度及峰值内摩擦角均增大，试样先剪缩后剪胀的变形特征更加显著。宏观结果与前人研究成果趋势一致，验证了本模型的可行性。

(2)转动阻抗的作用降低了砂体的平均力学配位数，但同时增大了砂试样内部强接触力的概率密度及其大小，而强接触力主要起抵抗外部荷载的作用，因此提高了砂的抗剪强度。

(3)随着抗转动系数的增大，接触法向和法向接触力各向异性均随之增大，法向接触力各向异性增强主要是强接触力各向异性的增加。从而使砂土内部力链结构更加稳定。