基于应变指标的斜拉桥桥塔地震损伤演化

李小珍，杨得海，赵鲁峰，辛莉峰，刘 鸣

(西南交通大学 土木工程学院，四川 成都 610031)

斜拉桥作为一种常见的大跨度桥梁结构，其抗震性能一直备受关注。目前相关桥梁抗震设计规范中，都只针对小跨、低墩的常规桥梁，对于大跨径高墩桥梁结构尚无明确有效的抗震评估方法，其抗震设计需作专门的研究[1]。大跨度铁路斜拉桥作为铁路交通网络中的重要枢纽，其投资大、荷载大，非线性行为显著，动力特性十分复杂。其对桥梁结构刚度以及运行平稳性、安全性方面有较高要求，且其桥塔的高度、截面尺寸以及自身重量均较大，在地震作用下动力响应显著，若在地震中发生破坏，将会带来严重的经济损失[2]。我国西部一直是地震频发区，相应的桥梁抗震防灾要求也更高。因此，有必要对西部高墩大跨度铁路斜拉桥的抗震性能及地震损伤情况作深入探讨。

目前斜拉桥的抗震分析中，抗震性能试验与数值模拟是两大主要分析手段。早期振动台试验主要开展构件或者小比例模型试验。近年来，振动台阵试验技术已得到快速发展，较多学者基于多子台阵振动台试验对斜拉桥在多种地震激励形式下的响应特性进行了研究。Yang 等[3]设计了双振动台测试系统，探究了非一致地震激励对不同塔梁连接形式的斜拉桥地震反应的影响规律；嵇冬冰等[4]对典型H型斜拉桥桥塔进行纵桥向振动台试验，研究其破坏过程；王瑞龙等[5]基于一座中等跨度的混凝土斜拉桥，设计了1∶20的大比例全桥振动台试验模型，探究了斜拉桥在强震下可能发生的破坏模式。孙利民等[6]以一座试设计的主跨为1 400 m的超大跨径斜拉桥为例，研究不同体系斜拉桥的地震响应和横向破坏模式。房贞政等[7]基于三台阵振动台试验研究了武汉二七长江大桥在多点地震激励下的响应规律，结果表明行波效应的影响不容忽视。然而目前的模拟振动台试验大多都仅针对单向地震动作用，且大部分研究对象为中小跨度斜拉桥，对于大跨度桥梁结构而言，振动台试验仍受限于振动台几何尺寸、承载能力以及试验经费等，需采用小比例缩尺模型，无法准确合理地模拟桥梁结构材料及边界条件[8]。因此，数值模拟仍是必要的分析方法，众多学者用数值模拟方法来研究斜拉桥桥塔的抗震性能。夏修身等[9]基于增量动力分析法研究了斜拉桥桥塔的非线性抗震性能，结果显示塔顶位移指标不能较好反映桥塔的地震损伤程度，桥塔屈服后仍有一定的抗震能力储备。徐艳等[10]分析了斜拉桥在顺桥向强震作用下的响应，得出在强震作用下，需考虑桥塔的非线性地震响应及其对桥梁整体抗震性能的影响。文献[11]表明斜拉桥桥塔的潜在塑性铰区域在顺桥向地震作用时为塔底与中塔柱，在横桥向地震作用时为塔底、中塔柱及上下横梁。谢文等[12]研究了大跨斜拉桥在一维地震动作用下的破坏模式，指出地震作用下大跨斜拉桥的主塔和桥墩属于易损构件，其地震损伤会受地震动频率成分的影响。文献[13-14]表明在进行结构抗震分析时，应充分考虑多维地震动激励的影响。

以往的研究中，桥塔在地震作用下的损伤状态评估较多采用塔顶位移、位移延性比、曲率延性比、曲率、应变等损伤指标[15]。对于较高的桥塔，截面曲率能充分反应桥塔的变形及转动性能，但当地震动多维输入时，曲率指标已不再适用。应变指标属于材料层面的物理量，且不受多维地震动输入的影响，能较好地描述桥塔在地震下的损伤状态，被广泛地应用于钢筋混凝土塔柱地震响应特性等方面的研究中[16-17]。综上所述，地震动作用下斜拉桥桥塔具有很强的非线性，需选取合适的损伤评定指标，来探讨其在多维地震动作用下的损伤演化过程。

本文基于OpenSEES平台，以某大跨度铁路钢桁梁斜拉桥为研究对象，建立了全桥的非线性有限元模型；分别以桥塔的截面曲率及纵向钢筋的应变作为桥塔的损伤指标，验证了二者在评估桥塔抗震性能时的等价性；选取典型的地震动记录，研究单向及双向水平地震动作用下的斜拉桥桥塔的地震损伤演化过程及破坏规律。

1 斜拉桥有限元分析模型

选取我国西部某铁路半漂浮钢桁梁斜拉桥为研究对象，其跨径布置为(81+135+432+135+81)m，速度为200 km/h客货共线双线铁路桥，立面构造见图1。该桥主塔顺桥向为单柱式、横桥向为花瓶形，10#塔高176.2 m，11#塔高181 m。桥塔采用单箱单室矩形截面，上横梁以下桥塔为变截面。材料方面，混凝土等级为C55，钢筋采用HRB335，竖向主筋采用直径32 mm、基本间距为130 mm，横向箍筋采用直径16 mm、基本间距为125 mm，局部加密为100 mm。斜拉索采用抗拉强度为1 770 MPa、直径为7 mm的热挤聚乙烯(PES)高强平行钢丝索。

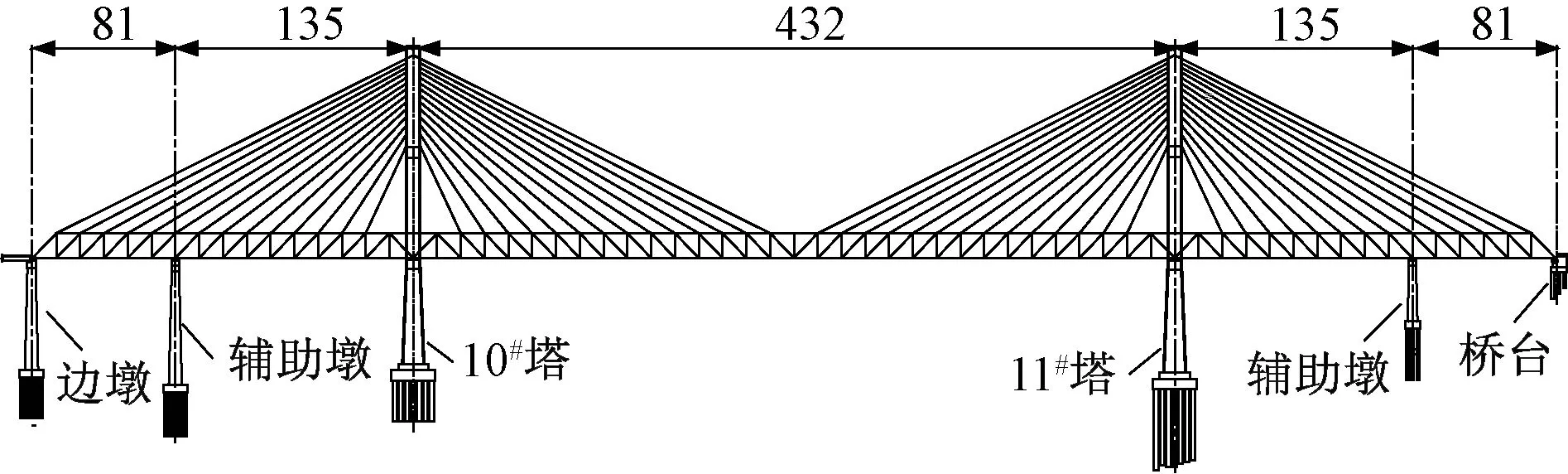
图1 斜拉桥立面图(单位：m)

基于OpenSEES软件，建立大桥的非线性分析模型。为简化考虑，建模时不考虑辅助墩和边墩单元，将其简化为对主梁的约束，见表1。根据以往相关学者对斜拉桥地震损伤的研究，主梁与斜拉索在地震反应中并不起控制作用[18]，故采用弹性梁柱单元(Elastic Beam Column)模拟主梁，斜拉索以桁架单元(Truss)来模拟，采用Ernst公式计算拉索的换算弹性模量，根据索的成桥拉力赋予其初始应力[19]。大桥的主塔与主梁连接的球形支座采用零长度单元(Zerolength)模拟桥塔，并根据支座特性赋予横桥向及竖向的材料强度，其他方向设为零。由于桥址处为Ⅰ类场地，故可忽略桩土效应对结构的影响，边界条件为塔底固结。

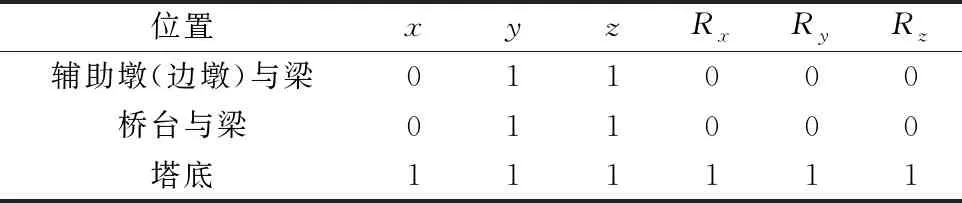
表1 模型边界条件

为更好模拟斜拉桥桥塔在地震作用下的损伤演化过程，采用OpenSEES中基于位移插值函数的弹塑性纤维梁柱单元(Disp Beam Column)模拟，每个单元设置5个高斯积分点，以变截面中间处的截面作为整个单元的截面，桥塔典型纤维截面具体划分型式见图2。

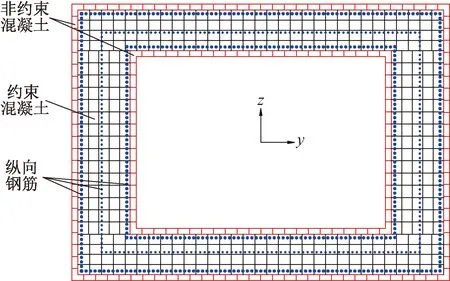
图2 桥塔纤维截面

材料方面，斜拉桥的桥塔和上下横梁的约束及非约束区混凝土均采用具有Kent-Scott-Park本构模型[20]的Concrete02混凝土材料进行模拟，详细参数见表2，其中fpc、ε0为混凝土抗压极限强度及极限应变，fpcu、ε为混凝土抗压退化强度及其应变。普通钢筋采用具有Giuffre-Menegotto-Pinto 本构关系模型[21]的Steel02来模拟。拉索采用Steel02材料并赋予其初拉力，钢材相应参数见表3。该斜拉桥桥塔支座的设计竖向承载力为25 000 kN，支座竖向以弹性材料Uniaxial Material Elastic模拟，支座横向采用Steel01材料来模拟其受力与变形间的关系[22]，其具体参数见表4。

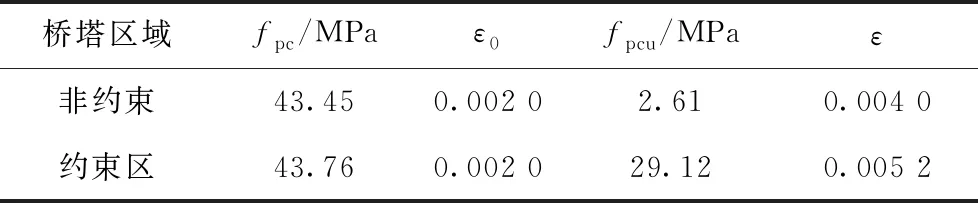
表2 混凝土材料参数

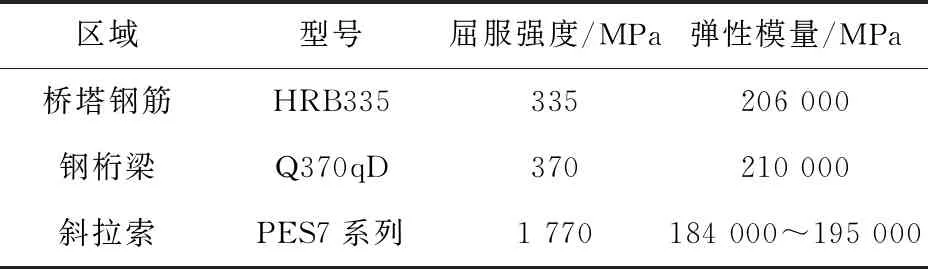
表3 钢材材料参数

表4 支座Steel01材料参数

全桥空间非线性有限元模型见图3。经过特征值分析，桥梁的前5阶自振周期及振型描述见表5，T1，T2分别代表OpenSEES与Midas软件中模型的自振周期，由表5可见，两种软件中的桥梁模型自振周期的结果吻合较好，这从而证明OpenSEES建立的全桥有限元计算模型是准确可靠的。

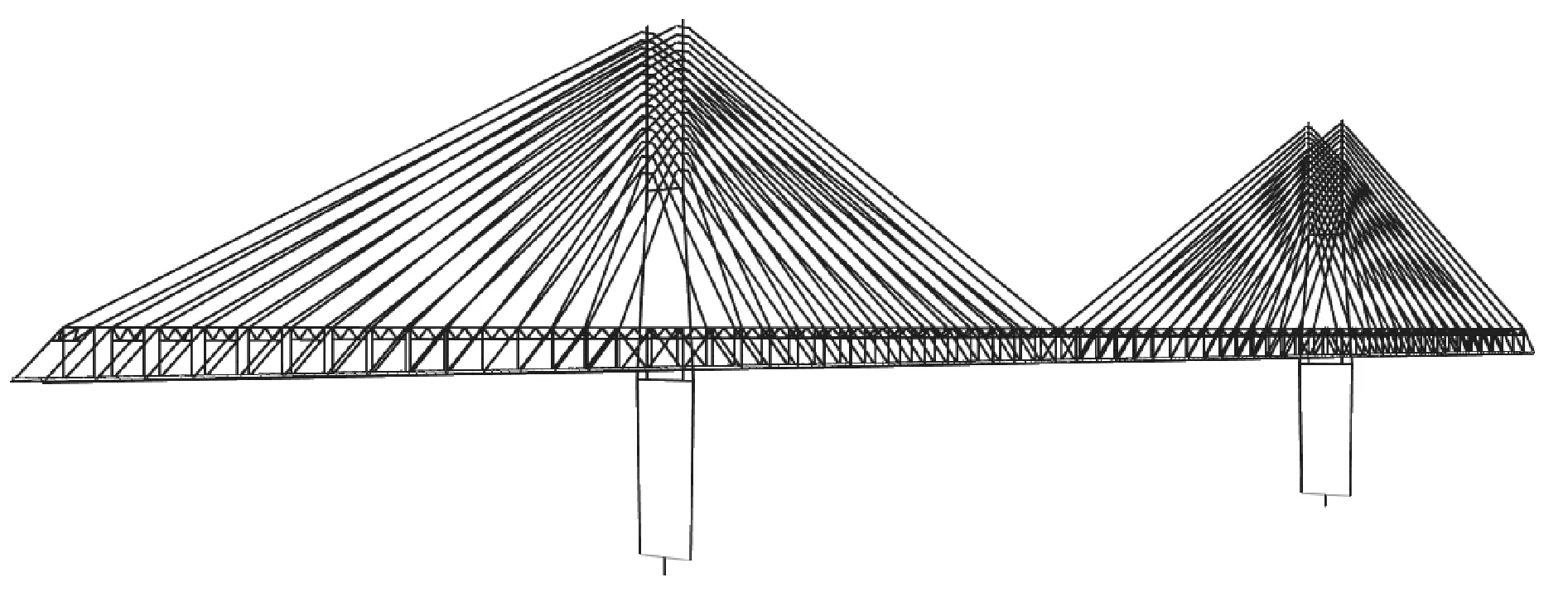
图3 全桥有限元模型

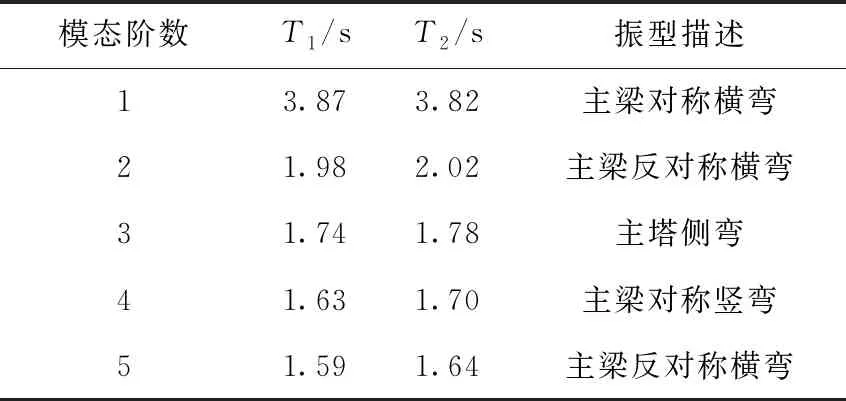
表5 桥梁前5阶自振周期及振型

2 损伤指标量化

2.1 地震动选取

地震动选取准则需考虑地震动的强度、频谱特性、强震持续时间。本次研究基于以上选取准则，考虑不同场地条件，不同频谱特性地震波对结构响应的影响，选择了卓越周期与结构自振周期较为接近的地震波。从太平洋地震研究中心(PEER)选取了具有代表性的三条地震波，分别是Imperial波、Landers波和Kocaeli波，三条地震波的卓越周期分别为0.58、1.24、0.38 s，其余相关参数见表6，加速度反应谱见图4，加速度时程曲线见图5。

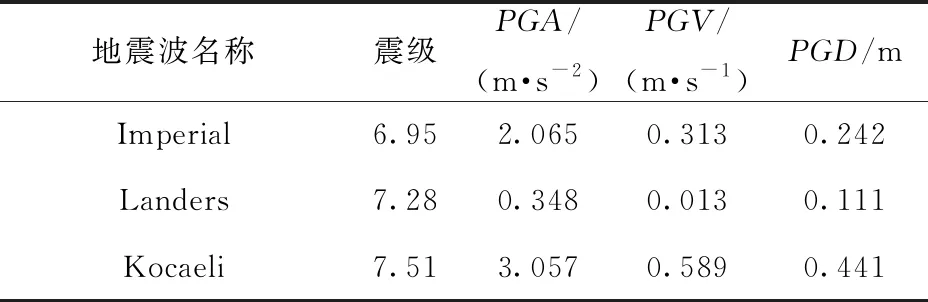
表6 地震波参数

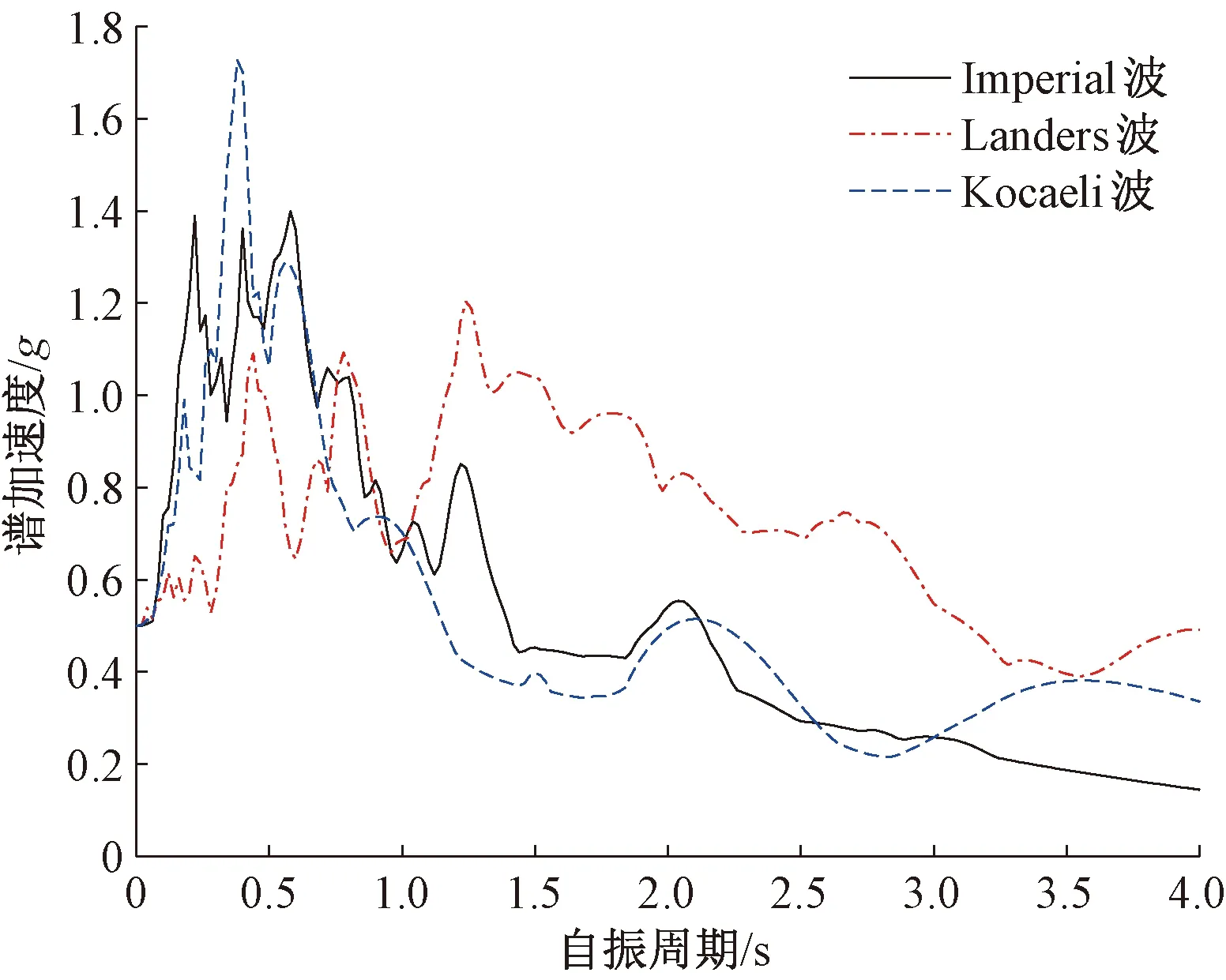
图4 地震波加速度反应谱曲线

图5 地震波加速度时程曲线

2.2 控制截面选取

选取斜拉桥的10#塔为研究对象，首先需确定有效的控制截面。参考文献[23]的分析方法，绘制出不同地震动输入条件时桥塔的截面曲率与截面最外侧纵向钢筋应变包络图。

以强震Imperial波为例，将其峰值加速度(PGA)调幅至0.1g～1.0g，沿桥梁纵向(顺桥轴线方向)输入，输出桥塔的截面曲率及最外侧纵向钢筋应变包络图见图6。而后，将2.1节选取的三条地震波的PGA均调幅至1.0g，同样沿桥梁纵向输入，输出桥塔的截面曲率及最外侧纵向钢筋应变包络图见图7。同样地，需寻求双向水平地震动作用下的桥塔控制截面。参考相关文献中关于双向地震动组合模式[24]，将Imperial波的PGA调幅至0.1g～1.0g，然后按照纵横向PGA比值为1∶0.85输入到结构中，作出Imperial波作用下桥塔钢筋应变的IDA包络图见图8(a)。将选取的三条波的PGA均调幅至1.0g，按纵横向PGA比值为1∶0.85输入到结构中，作出多条波作用下桥塔各个截面最外侧纵向钢筋应变包络图见图8(b)。

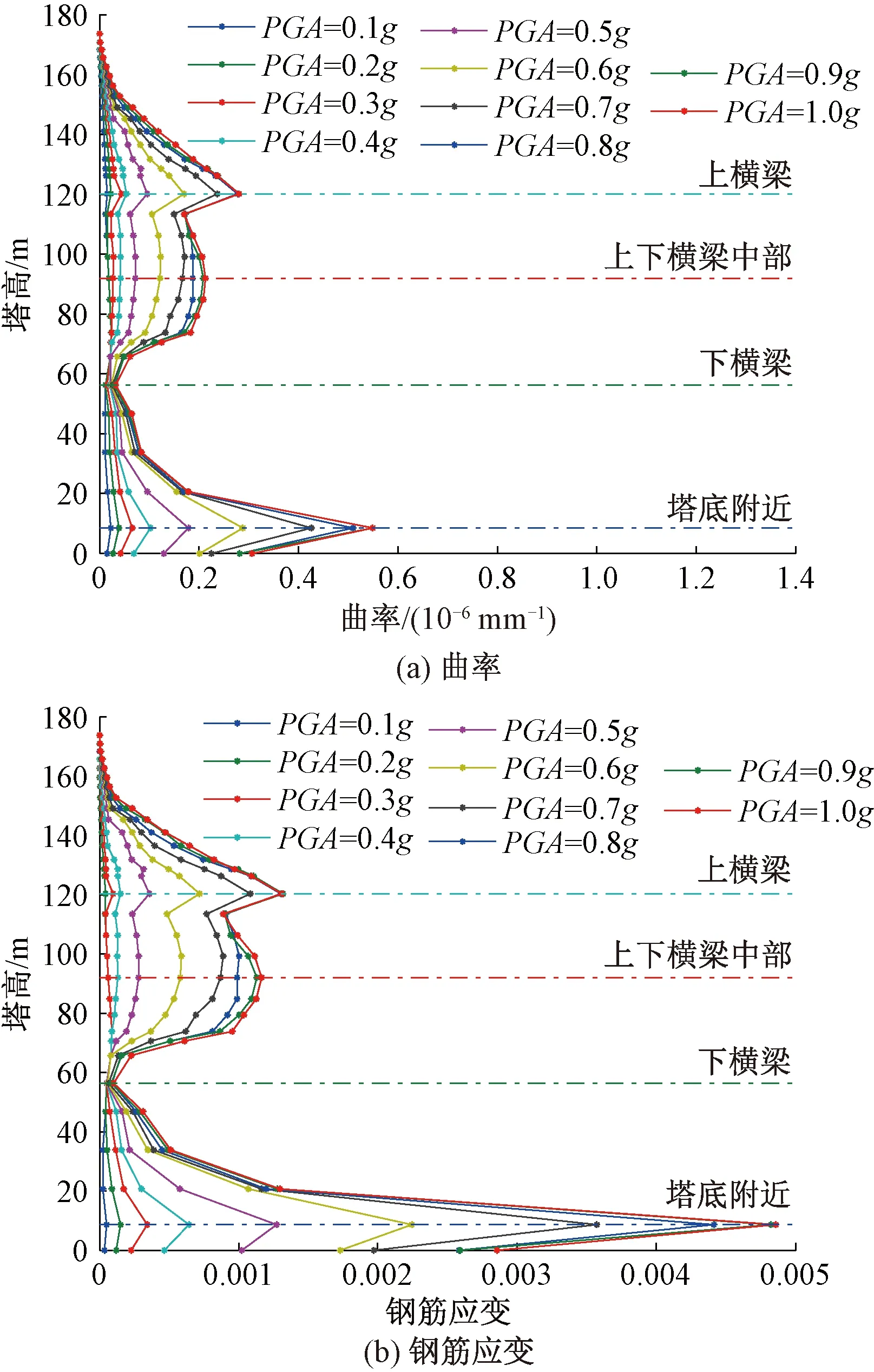
图6 Imperial地震波纵向输入时桥塔截面曲率及最外侧纵向钢筋应变IDA包络图

由图6、图7可知，不同强度的Imperial波与多条波纵向输入时，桥塔的截面曲率与钢筋应变沿桥塔高度的变化规律基本一致。均在塔底附近、中塔柱(桥塔上横梁与下横梁间的中部区域)以及上横梁处取得极大值，在下横梁及上横梁附近取得极小值。当多条地震波输入时，上下横梁间中部区域的极值点更偏向于下横梁，这是由于不同地震波具有不同的频谱特性所导致的。对比图6～图8，能清晰地发现，双向地震动与纵向地震动分别作用时，桥塔的控制截面完全一致。总体来看，截面曲率及钢筋应变沿桥塔由下及上均呈先增后减，再增再减的趋势。这充分反映了钢筋应变指标与截面曲率指标间的协调性，也在一定程度上表征了桥塔纵向钢筋的应变作为损伤指标的良好适用性。

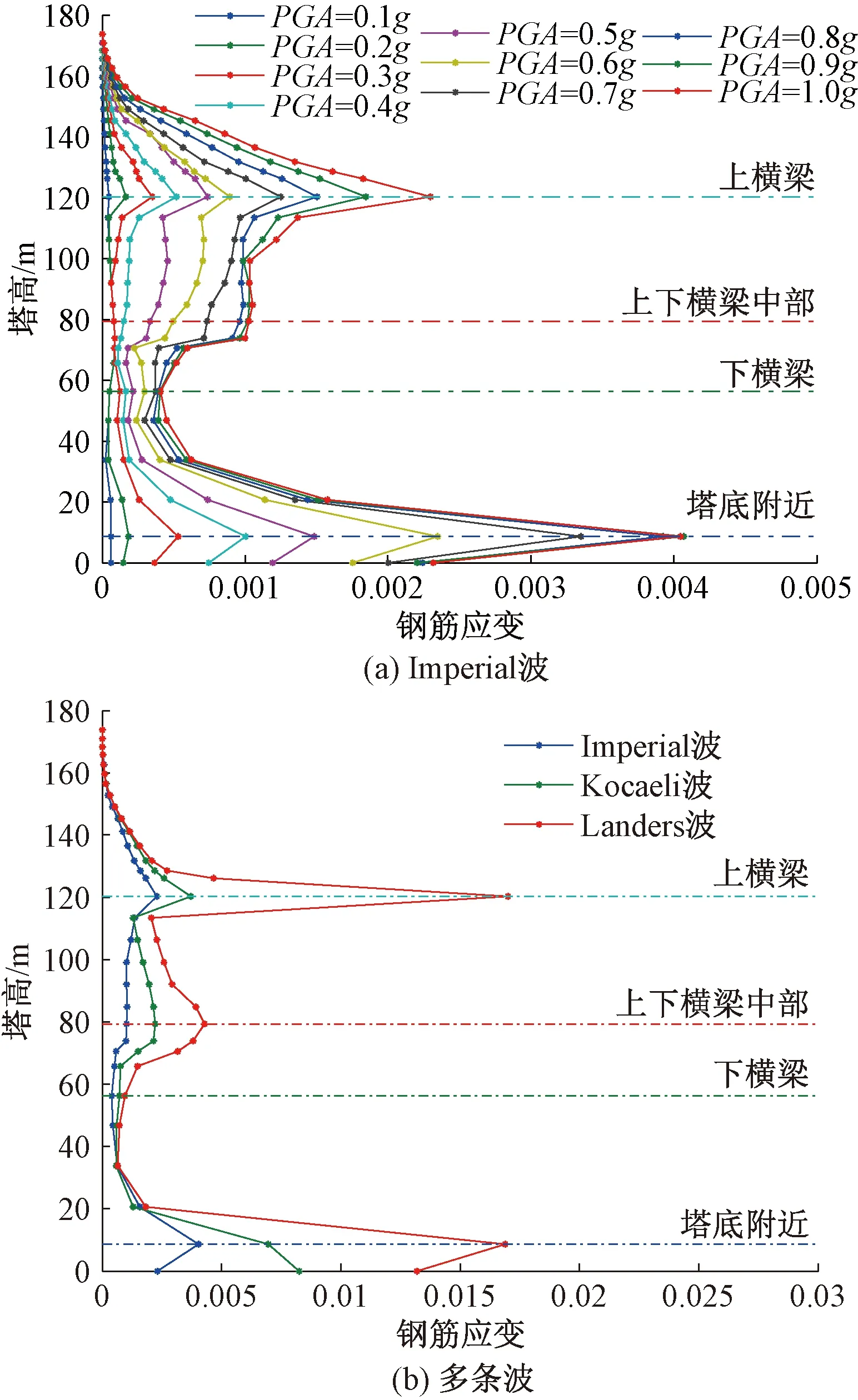
图8 地震波双向输入时桥塔截面最外侧纵向钢筋应变包络图

经过对不同地震动输入模式下钢筋应变的需求分析，以多条地震动纵向输入时桥塔的截面曲率与钢筋应变的极大值点所在截面作为桥塔损伤演化的控制截面，即塔底截面、塔底附近截面、中塔柱(上下横梁中部区域)以及上横梁处。桥塔控制截面示意位置见图9。

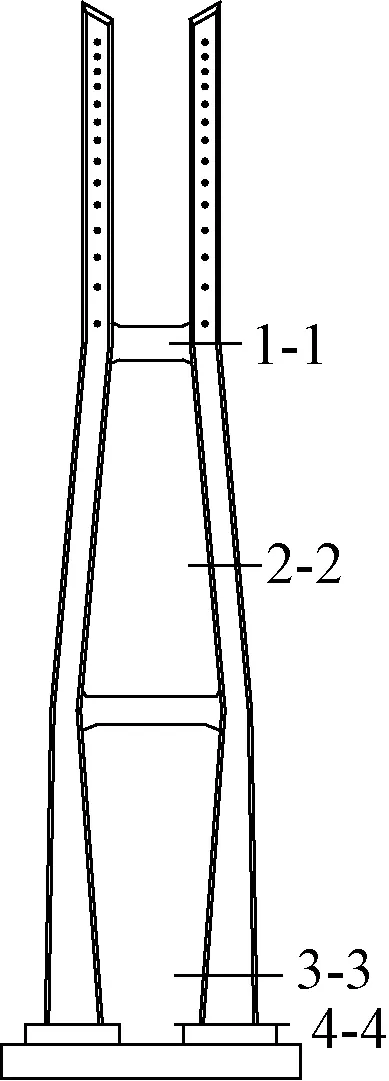
图9 桥塔控制截面

2.3 曲率与应变损伤指标量化

为了得到桥塔在各损伤状态下的曲率损伤指标临界值，需对关键截面进行弯矩-曲率分析，继而根据JTG/T 2231-01—2020《公路桥梁抗震设计细则》[25]中的面积相等原则，得到各个控制截面的等效曲率以及极限曲率。通过分析各个关键截面不同损伤状态的临界曲率如表7所示，其中,φy为截面最外侧纵向钢筋首次屈服时的截面曲率；φey为根据面积相等原则确定的等效屈服曲率；φb为截面外侧钢筋拉应变达到0.006时对应的截面曲率；φu为约束区混凝土压应变达到0.004时的截面曲率。以这4个曲率作为判定截面损伤状态的临界曲率指标。

表7 桥塔控制截面临界曲率

对于纵向钢筋应变的各个损伤状态的临界值，参考有关学者的研究[24]，以HRB335钢筋的屈服应变0.001 675作为轻微损伤的临界值，其余损伤状态临界值则与截面弯矩-曲率分析相对应。综合分析可以得到各个损伤状态下截面曲率及钢筋应变指标取值如表8所示。

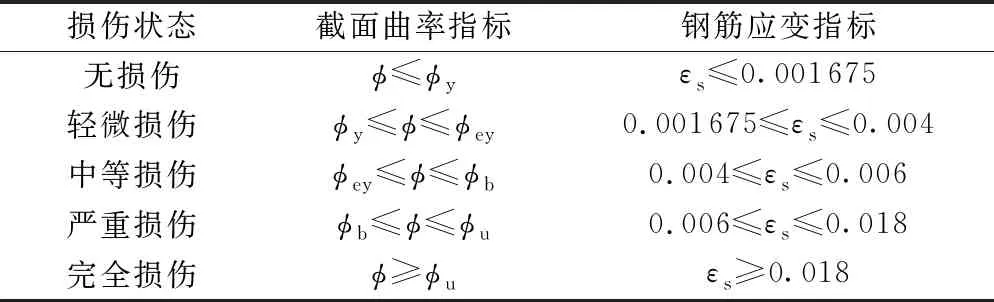
表8 钢筋应变与截面曲率损伤指标对应关系

3 纵向地震动作用下钢筋应变与曲率指标对比

3.1 以截面曲率为损伤指标

分别将Imperial波、Landers波及Kocaeli波的PGA调幅至0.1g～1.5g，然后沿着纵桥向输入，输出不同地震动作用时10#塔各个关键截面在不同PGA强度下的峰值曲率，结果见图10。由图10可见，不同地震波纵向输入时，桥塔各个控制截面的损伤情况，3-3截面>4-4截面>2-2截面>1-1截面。从地震波的破坏情况来看，同Imperial波相比，地震波Kocaeli波与Landers波对结构的破坏性更强，尤以Landers波为最，这从地震波的反应谱特性也可以明显看出来，Landers波的卓越周期为1.24 s，与桥梁的一阶自振周期3.87 s更为接近，故而引起的桥梁响应更大。另外，根据地震波反应谱曲线，在桥梁的自振周期3.87 s附近，与Imperial波相比，地震波Kocaeli波与Landers波这两条波的谱加速度更大，由此引发的桥梁结构地震响应也更加剧烈。

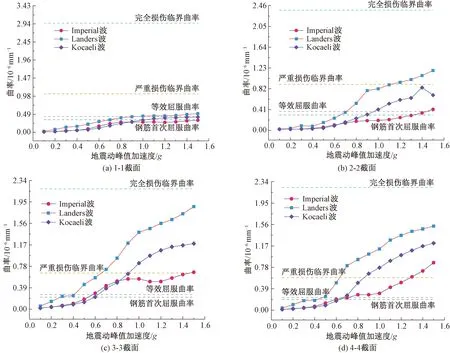
图10 不同地震波纵向输入时桥塔各关键截面曲率IDA曲线

3.2 以材料应变为损伤指标

同样地，以纵向钢筋的应变作为损伤指标，输出不同地震动纵向输入时10#塔的各个关键截面在不同PGA强度下的钢筋峰值应变，结果见图11。由图10、图11可知，截面曲率损伤指标与钢筋应变损伤指标在不同地震动纵向输入时，随地震动峰值加速度的发展规律基本一致。同时，绘出桥塔3-3截面在Landers波纵向输入时不同损伤指标下的损伤状态对比，见图12。横坐标代表地震波的峰值加速度，纵坐标表示其损伤程度，定义0代表无损伤状态，1为轻微损伤，2为中等损伤，3为严重损伤，4为完全损伤。从图12可以清晰地看出两种指标的一致性，这再一次验证了钢筋应变作为损伤指标的可靠性。

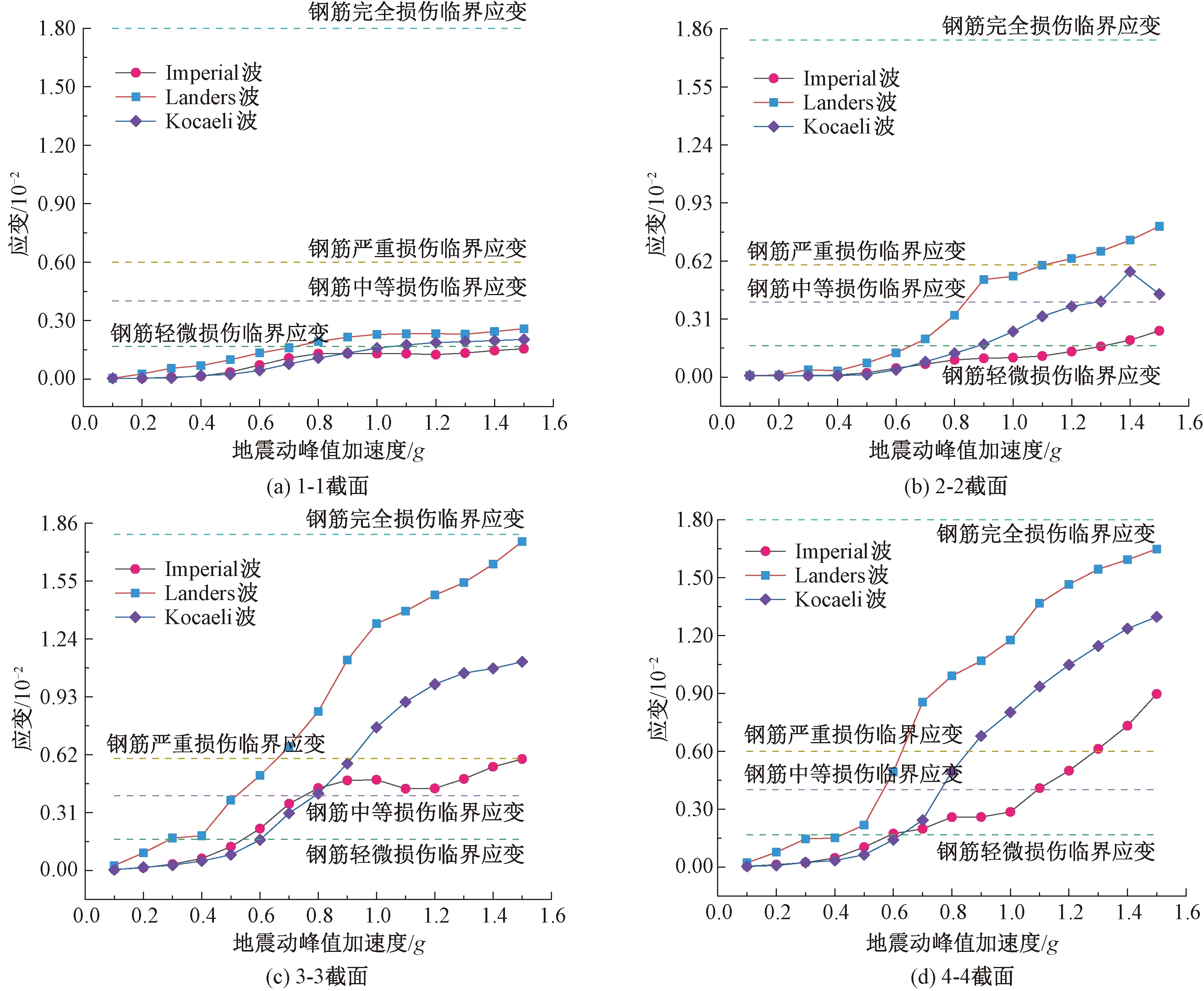
图11 不同地震波纵向输入时桥塔各关键截面应变IDA曲线

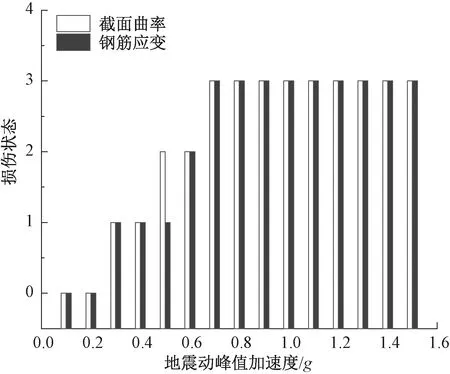
图12 Landers波纵向输入时3-3截面两种指标损伤对比

4 双向水平地震动作用下桥塔损伤演化模拟

4.1 双向水平地震动作用下桥塔峰值应变

通过前面的分析，验证了钢筋应变作为桥塔地震损伤评定指标的可行性，现将其应用于地震波双向输入。将2.1节中选取的Imperial波、Landers波及Kocaeli波的PGA调幅至0.1g～1.5g，然后按照纵横向PGA比值为1∶0.85输入到结构中，输出三条地震动下桥塔各个关键截面在不同PGA强度下的峰值应变，结果见图13。由图11～图13可知，双向水平地震动作用明显增大了桥塔各个关键截面的峰值应变。PGA为1.5g的Landers波在纵向及双向输入时桥塔各个关键截面的峰值应变对比情况见表9。由表9可知，双向地震波输入时，桥塔各个关键截面的钢筋应变均有大幅增加，尤其是上横梁位置处的1-1截面的增幅最大。通过对比纵向与双向地震动作用下桥塔各个关键截面的峰值应变，充分说明了在大跨度桥梁的地震损伤演化研究中，不容忽视双向水平地震动的组合作用。

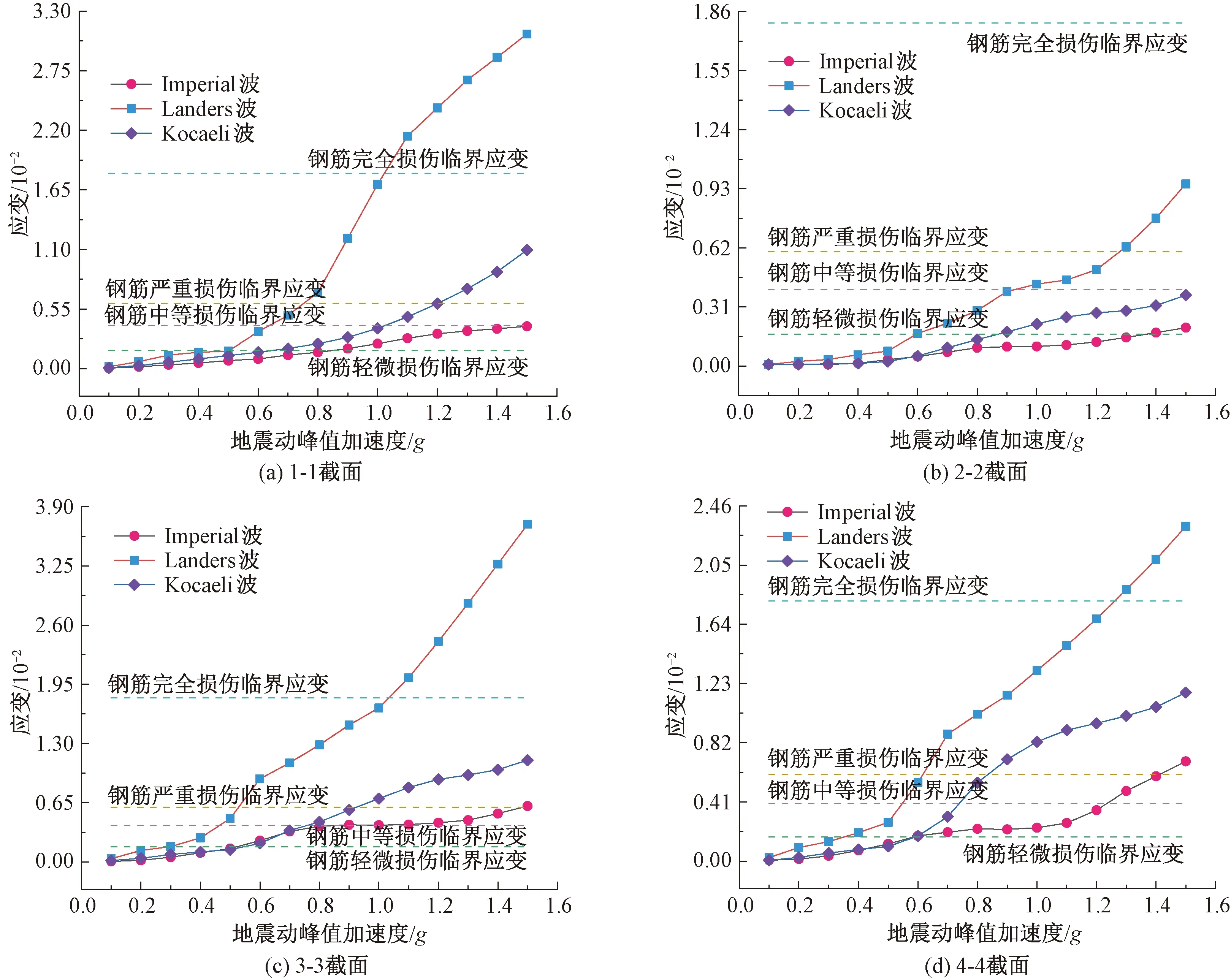
图13 不同地震波双向输入时桥塔各关键截面应变IDA曲线

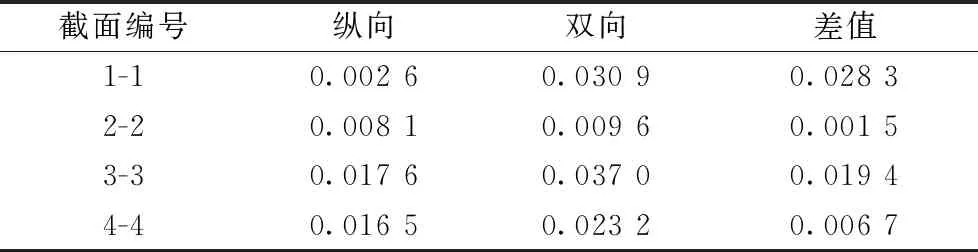
表9 桥塔关键截面最不利应变响应对比

4.2 桥塔地震损伤演化

桥塔的地震损伤演化过程可通过损伤演化柱状图来模拟。以钢筋应变作为损伤指标，10#塔在不同地震动纵向及双向输入时的损伤演化柱状图见图14，横坐标表示地震波的峰值加速度(PGA)，纵坐标表示损伤程度。由图14能清晰地判断在不同PGA作用时，桥塔各个关键部位所处的损伤状态以及整个桥塔在地震作用下的损伤演化过程。以图14 (a)为例，通过损伤演化柱状图，能明显看出桥塔在PGA小于0.5g时，各个关键截面均处于良好工作状态，直至PGA达到0.6g时，桥塔的3-3与4-4截面(即塔底附近截面)，首次达到屈服状态。随着PGA的不断增加，3-3与4-4截面损伤程度不断加剧，2-2截面也逐渐达到屈服，1-1截面全程处于无损伤状态。这与嵇冬冰等[4]所做的斜拉桥桥塔纵桥向振动台试验得出的结论一致：随着纵向地震动输入等级的增大，下塔柱、中塔柱先后出现裂缝，塔底以上30 cm范围内损伤最为明显。由图14可知，PGA小于0.7g时，两种地震动输入模式下桥塔的损伤演化曲线完全一致。随着PGA的增加，纵向地震动下一直处于无损伤的1-1截面在双向地震动PGA为0.9g时也进入屈服状态。可以看出，相较于单独的纵向地震波输入，地震波双向输入时，桥塔的1-1截面(上横梁处)的损伤程度更为严重。这是由于横向地震波的加入，导致上横梁处截面较快进入屈服状态，出现明显的损伤，该结论也与较多关于斜拉桥横桥向地震破坏性试验得出的结果类似[5-6]。同Imperial波及Kocaeli波相比，Landers波双向较纵向输入时桥塔的损伤程度增加更为显著。

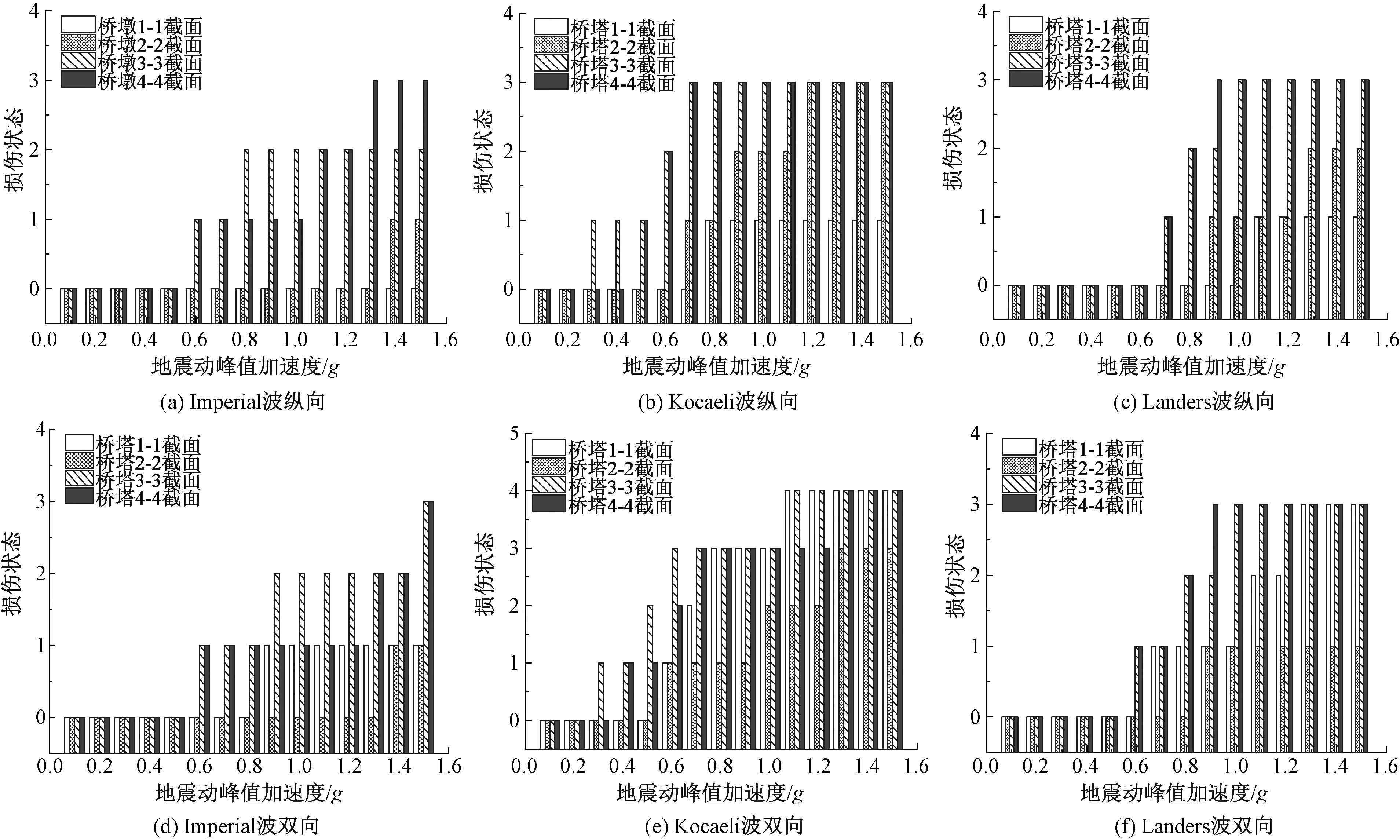
图14 不同地震波纵向及双向输入时桥塔损伤演化对比图

综合而言，单独的纵向地震波输入时，桥塔的损伤演化顺序是由塔底至塔顶，各个控制截面的逐渐出现损伤，塔底的损伤程度更为剧烈。双向水平地震波输入时，桥塔的损伤依然始于塔底，而后上横梁附近截面达到屈服，再发展至中塔柱。故双向地震动会改变桥塔的损伤演化顺序，在模拟地震作用下桥梁的损伤演化过程时需注意地震动不同输入方式的影响。

5 结论

本文以主跨为432 m的铁路钢桁斜拉桥为研究对象，验证了截面纵向钢筋应变作为损伤指标在纵向及双向地震波输入时的可靠性，并以此分析了地震动作用下大跨度铁路斜拉桥桥塔的损伤演化过程。通过本次研究，可以得出如下结论：

(1)大跨度铁路斜拉桥桥塔在地震作用下的主要控制截面为塔底、上横梁及中塔柱(桥塔上下横梁间的中部区域)，在桥塔抗震设计中，应予以重点关注。

(2)桥塔截面纵向钢筋应变是一种较为可靠的损伤指标，当地震动单向输入时，钢筋应变与截面曲率两种指标计算结果吻合较好。

(3)相较于纵向地震动，双向水平地震动作用会显著加剧斜拉桥桥塔的损伤，同时会改变斜拉桥桥塔损伤演化顺序：当地震波纵向单独输入时，桥塔的塔底先出现损伤，接着是中塔柱，最后是上横梁处；而在双向水平地震动作用下，桥塔的塔底仍最先出现损伤，继而是上横梁处，最后是中塔柱。