高速铁路车站高峰时段通过能力计算方法
熊 亚,李海鹰,廖正文,王 莹,牛鑫涛
(1.北京交通大学 轨道交通控制与安全国家重点实验室, 北京 100044;2.北京交通大学 交通运输学院 , 北京 100044;3.中国铁路太原局集团有限公司 太原站,山西 太原 030031)
随着高速铁路(以下简称高铁)运输需求不断增加,高铁车站能力紧张的问题日益凸显。特别是在旅客出行的高峰时段,列车到达、出发密度较高,如何合理地协调咽喉和到发线的运用,提高车站通过能力,以更好地满足旅客出行需要显得尤为重要。对此,TB 10621—2014《高速铁路设计规范》[1]规定应根据车站设施配置和作业组织方案,计算高峰时段车站通过能力。
高铁车站的高峰时段通过能力是在列车到发密集时段内特定的行车组织方式下的最大接发列车数量,为高峰时段车站合理、高效的作业组织提供依据。文献[1]计算高铁车站(高峰时段)通过能力所使用的综合分析法,遵照了既有线车站以利用率计算法为基础的经典理论体系和计算方法。
该理论算法基于客货混行的普速铁路运输组织模式发展而来,存在一些固有缺陷:①算法以解耦的方式处理咽喉与到发线的关系,独立计算二者的通过能力,忽略了列车对二者占用的时空连续性。②方法中的空费系数往往需要根据经验估算,一定程度上影响了通过能力计算的准确性。③这种算法难以计算繁忙的高峰时段,咽喉和到发线协调配合下车站最大接发车数量,且得到能力平均值对于车站工作组织缺乏实际指导作用。因此,有必要根据高铁的运营特点,研究更准确的高峰时段车站通过能力计算方法,以更好地指导高铁运输组织。
高铁车站一般不办理货运业务,而且在高峰时段通常只办理动车组列车的接发作业,不办理动车组出入段作业,以免占用咽喉通过能力。相较于普速铁路车站,高铁车站技术作业更单一,但列车接发密度更高,对通过能力计算的精确性要求更高。
国内外专家对高铁车站的通过能力及其计算方法进行了专门的研究。Astengo等[2]通过计算机模拟列车占用轨道情况,研究车站布局等因素对高铁车站通过能力的影响。Jensen等[3]对UIC406(国际铁路联盟出版描述铁路能力的手册)方法进行了改进和拓展,建立了能力评估模型,刻画铁路设施占用情况、计算能力消耗。杜文等[4]探究了客运站通过能力的仿真模型及设计流程。颜颖等[5]基于周期化作业实现能力最大化的思路,利用车站技术作业图表铺画的方法建立客运站通过能力运用关系模型,得到能力最大化时车站最优作业方案。刘敏等[6]通过压缩和加密车站作业方案的方法挖掘高铁车站的可用能力,并进行仿真模拟。陈韬等[7]以尽可能多地接发列车为目标,建立高铁客运站通过能力计算模型,并提出分阶段决策优化和禁忌搜索算法相结合的求解算法。杜彦华等[8]构建了基于计算机仿真的层次拓展模糊时间Petri网以求解车站通过能力。钟俊[9]建立最大平行进路的网络流模型,并提出相应的求解算法。刘佩[10]对车站间隔时间进行了细致研究,建立以最小化停站时间为目标的高峰时段通过能力计算模型,运用分支定界法求解。张嘉敏[11]提出了双层模型体系:总体层模型确保列车占用股道时间最小,在此基础上进行局部层冲突检验与进路选择优化,进而计算车站能力。吴佳珂[12]提出基于智能体的高铁车站通过能力仿真模型,以AnyLogic为仿真平台,建立实例仿真系统。闫学成[13]提出道岔自动分组算法,并给出道岔组的非空闲时间统计方法,在此基础之上建立车站通过能力自动仿真模型。王宇强等[14]将车站虚拟为区间,采用平均最小列车间隔法计算虚拟区间通过能力。
既有研究较少对列车在高铁车站内的作业过程进行细致的刻画和模拟,因而得到的车站通过能力计算结果的准确性有待提高。其中,虽然刘佩[10]考虑高铁分段解锁特性,提出车站间隔时间精细化计算方法,为高铁车站能力计算提供了更为准确的输入参数,但是对于列车立即折返产生的车站到、发进路及到发线占用关联考虑较少,因而未能完全刻画咽喉与到发线占用的关联关系。
为更加准确地刻画高铁车站作业特征,提高车站能力计算准确性,本文以轨道电路区段为列车作业占用最小单元,对车站高峰时段的典型作业进行精细刻画,提出高铁车站高峰时段通过能力计算方法。
1 高铁车站高峰时段通过能力问题分析
依据图解法铺画“饱和车站作业方案”以计算车站通过能力的思想,通过在既有的车站作业方案上不断添加列车,并对列车作业进行优化,直到给定的时域内车站无法继续添加列车为止,则最终的车站作业方案中接发车的数量即为车站在该时域的通过能力。
图解法求解车站通过能力的核心在于车站作业方案的优化:为列车安排到发线及其对应的接、发车进路,给出到发线、咽喉的合理使用方案,在满足客运作业规定的时间和作业股道的要求下,减少交叉干扰,最小化作业占用设备时间,利用最少的车站设备占用时间完成尽可能多的车站作业。
为了应对高峰时段列车到发密集的特点,车站需要采用特定的行车组织方法:期间不安排动车组出入段、所,不约束车次停靠股道,不安排特殊作业如上水、吸污等。本文计算的车站高峰时段通过能力,是在这种特定的行车组织方法下,车站在高峰时段所能接发或通过的最大旅客列车数。根据高峰时段行车组织特点,列车在高铁车站的作业过程见图1。

图1 列车作业过程
由图1可知,从列车运行的角度出发,可以将通过列车和“本线立折”列车的作业过程看作1对在同一到发线上连续发生的接、发车作业。对于“转线折返”列车,其作业过程可以看作2对连续发生的接、发车作业,分别在到发线a、b上完成。特别地,经由发车进路a的作业和经由接车进路b的作业需要在同一折返线上完成,因此这两项作业也可以看成1对在折返线上连续发生的“接、发车作业”。由于折返线与到发线性质相似,以下不再特别说明。通过这种描述方式,可以将车站办理的列车作业统一描述为1次或多次连续的接、发车作业。
对于衔接多条线路的高铁车站,如果多条线路合场设置,可以依据不同的接、发车方向将作业类型细化到各个方向(如a方向接车作业、b方向接车作业),并生成对应方向的接、发车进路备选集合;如果多条线路分场设置,可以分别计算各车场的通过能力,再进行汇总得到全站的通过能力。
列车在车站的作业需要满足以下时间和空间的约束:
(1)列车接发车进路选择与到发线选择的关系

(2)进路分段解锁
任意一项列车作业on∈O,都只能选择一条进路。如果on选择进路rm∈R,那么在作业发生前,车站CTC系统将触发指令,锁闭rm上所有轨道电路区段Crm,为作业占用做准备。随着列车经过并离开,轨道电路区段分段解锁。当列车完全出清一段轨道电路区段ck∈Crm后,ck自动解锁。son,ck、eon,ck为作业on选择的进路上轨道电路区段ck的锁闭和解锁时刻。
列车作业进路上各轨道电路区段的锁闭时刻和解锁时刻与作业发生时刻存在一定关系。如图2所示,接车作业o1∈OI选择进路r1∈R,占用轨道电路区段的顺序为c1→c2→c3,其中c1、c2为咽喉轨道电路区段,c3为到发线轨道电路区段,图中阴影表示轨道电路区段被占用,以下同。例如,c1的锁闭时刻so1,c1、解锁时刻eo1,c1与列车作业发生时刻to1存在等式关系

图2 轨道电路区段分段解锁示意图
so1,c1=to1+go1,c1
eo1,c1=to1+ho1,c1
式中:go1,c1、ho1,c1分别为作业进路上轨道电路区段c1锁闭时刻so1,c1和解锁时刻eo1,c1与作业发生时刻to1的差值,均为负值(负值表示so1,c1、eo1,c1早于to1)。
假设型号和编组均相同的动车组列车进站速度及加速度相同,则上述轨道电路区段锁闭、解锁的时刻与列车作业发生时刻的差值可以通过列车运行计算或现场调研获得,以精确地刻画列车作业过程。
(3)轨道电路区段占用唯一性
任意一段轨道电路区段同一时刻最多只能被一项作业占用。若两条进路rm1、rm2∈R存在重叠的轨道电路区段,即∃ck∈Crm1∩Crm2,则在空间上存在潜在冲突的可能。为了避免冲突,在时间上,选择这两条进路的列车作业on1、on2∈O需要按一定的次序占用ck,保证一项作业占用ck的解锁时刻早于另一项作业占用ck的锁闭时刻:eon1,ck≤son2,ck或eon2,ck≤son1,ck。
北京南站城际场东端咽喉轨道电路区段示意见图3,其中1~15为咽喉轨道电路区段,16~22为到发线轨道电路区段。发车作业o2∈OJ选择进路r2∈R,Cr2= {c4,c5,c6,c7,c8,c9,c15,c21};接车作业o3∈OI选择进路r3∈R,Cr3={c1,c2,c3,c8,c9,c15,c22}。两项作业选择的进路具有相同的轨道电路区段:c8、c9、c15∈Cr2∩Cr3。以c8为例,这两项作业占用c8时需满足先后顺序要求:eo2,c8≤so3,c8或eo3,c8≤so2,c8。
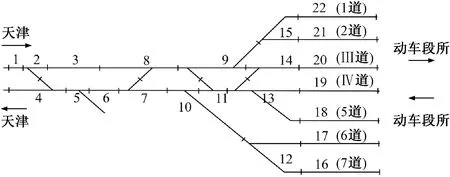
图3 北京南站城际场东端咽喉轨道电路区段图
2 高铁车站高峰时段通过能力计算方法
基于以上对高铁车站作业的分析,根据图解法的计算思路,提出高铁车站高峰时段通过能力的计算方法。
2.1 计算流程
Step1根据车站车场布局、既有车站作业方案,得到初始接、发车作业集OI、OJ,设置高铁车站的高峰时段为[Tl,Tu],Tl、Tu分别为高峰时段的开始与结束时刻。
Step2建立(更新)车站作业方案优化模型,输入初始(更新)的列车作业集OI、OJ,调用整数规划求解软件求解车站作业方案优化模型(具体见2.2节)。
Step3如果Step2求得可行解,表示高峰时段内车站可以接发所有列车并得到作业方案,跳转至Step4;如果Step2无可行解(或在给定的计算时间内未搜索得到可行解),跳转至Step5。
Step4基于既有车站作业方案中不同种类列车比例增加1列车v,其接、发作业(oiv,ojv)的时刻上、下界分别设定为Tu、Tl,按照作业类型指定作业进路备选集合,更新列车作业集合OI=OI∪{oiv}、OJ=OJ∪{ojv},返回Step2。

其中,Step4增加列车的原则为保证车站列车结构不变。例如,既有车站作业方案中不停站通过列车∶停站通过列车∶折返列车数量≈1∶2∶1,则按照第1次不停站通过列车,第2、3次停站通过列车、第4次折返列车的顺序依次添加列车。在保证列车结构不变的原则下,循环地向既有车站作业方案中添加列车,直至车站作业方案不能再加入列车为止。在加入列车过程中,新加入列车的作业时刻可以在整个高峰时段内调整,即新加入的列车可以“见缝插针”式地加入到既有车站作业方案中,同时既有车站作业方案中的列车作业时刻也可在一定范围内调整,以充分利用车站的通过能力。
通过能力计算方法流程见图4。

图4 通过能力计算方法流程图
2.2 车站作业方案优化模型
由图4可知,通过能力计算的核心是车站作业方案优化模型。模型的求解一方面可以判断当前在列车作业集合OI、OJ中的作业是否可以全部被安排在高峰时段的车站作业方案中,另一方面可以优化调整作业时刻,以实现各项作业占用设备的总时间最小。模型如果存在可行解,表示车站能够办理当前数量的列车作业。这时,模型进一步求得的最优解表示当前数量列车作业占用车站设备时间最小的作业方案,该作业方案及其对应的设备总占用时间可以用于衡量车站的能力利用率,也可以为车站设备可用能力挖掘提供更多空间。而如果模型无解,表示车站能力不能满足当前数量列车作业办理的能力需要。
通过求解车站作业方案优化模型,可以得到每次添加列车后,当前数量列车作业占用车站设备时间最小的优化作业方案。因此,最后得到的优化车站作业方案是饱和的,是在既有车站作业方案的列车结构下,按高峰时段特定行车组织方法,能够得到的高峰时段接、发车数量最多的作业方案,其接、发列车数量即为高速铁路车站高峰时段的通过能力。
2.2.1 模型假设
(1)假设相同型号、编组的列车进站、出站速度及加速度相同。
(2)高峰时段车站咽喉区接发车作业密集,不宜安排动车组出入段占用紧张的咽喉通过能力,因此假设所有列车在高峰时段无出入段作业。
2.2.2 模型符号
参数、集合及决策变量见表1~表3。

表1 参数及含义

表2 集合及含义

表3 决策变量及含义
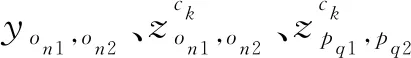
2.2.3 模型建立
为了使咽喉和到发线衔接紧凑,减少车站设备的占用时间,考虑在满足所有作业的情况下,以到发线的占用时间最小为优化目标,可以求解得到一个能力利用最优的车站作业方案。优化目标为
(1)
考虑进路选择、冲突疏解和区间追踪间隔等因素,模型的约束条件如下。
(1)进路选择唯一性
(2)
xon,rm∈{0,1} ∀on∈Orm∈Ron
(3)
约束式(2)、式(3)表示任意作业on∈O,只能在可能的进路集合Ron中选择1条进路作业,从而保证作业选择进路的唯一性。
(2)列车站内走行空间连续性
(4)
约束式(4)表示具有连续关系的接、发车作业对(oi、oj)∈P选择的进路需满足一致性要求,即若发车作业oj选择进路rm,则接车作业oi选择的进路对应的到发线须与进路rm对应的到发线一致,满足要求的进路集合记为Rrm。
(3)轨道电路区段占用时间约束
∀on∈Ock∈CL∪CT
(5)
∀on∈Ock∈CL∪CT
(6)
约束式(5)~式(6)表示作业on可行进路集合Ron中任意进路rm∈Ron均不经过轨道电路区段ck时,区段ck锁闭、解锁时刻为0 ;否则,其锁闭、解锁时刻存在且与作业发生时刻有如下约束:
锁闭时刻约束为
(1-xon,rm)×M+son,ck≥ton+gon,ck
∀on∈Orm∈Ronck∈Crm
(7)
son,ck≤ton+gon,ck+(1-xon,rm)×M
∀on∈Orm∈Ronck∈Crm
(8)
解锁时刻约束为
(1-xon,rm)×M+eon,ck≥ton+hon,ck
∀on∈Orm∈Ronck∈Crm
(9)
eon,ck≤ton+hon,ck+(1-xon,rm)×M
∀on∈Orm∈Ronck∈Crm
(10)
当作业on选择的进路rm经过轨道电路区段ck时,xon,rm=1,约束式(7) ~式 (10)合成为:son,ck=ton+gon,ck、eon,ck=ton+hon,ck,表示作业发生时刻和进路上轨道电路区段锁闭、解锁时刻的关系。
(4)咽喉作业冲突疏解约束
∀on1、on2∈Ock∈Con1∩Con2∩CT
(11)
∀on1、on2∈Ock∈Con1∩Con2∩CT
(12)
∀on1、on2∈Ock∈Con1∩Con2∩CT
(13)
∀on1、on2∈Ock∈Con1∩Con2∩CT
(14)
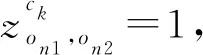
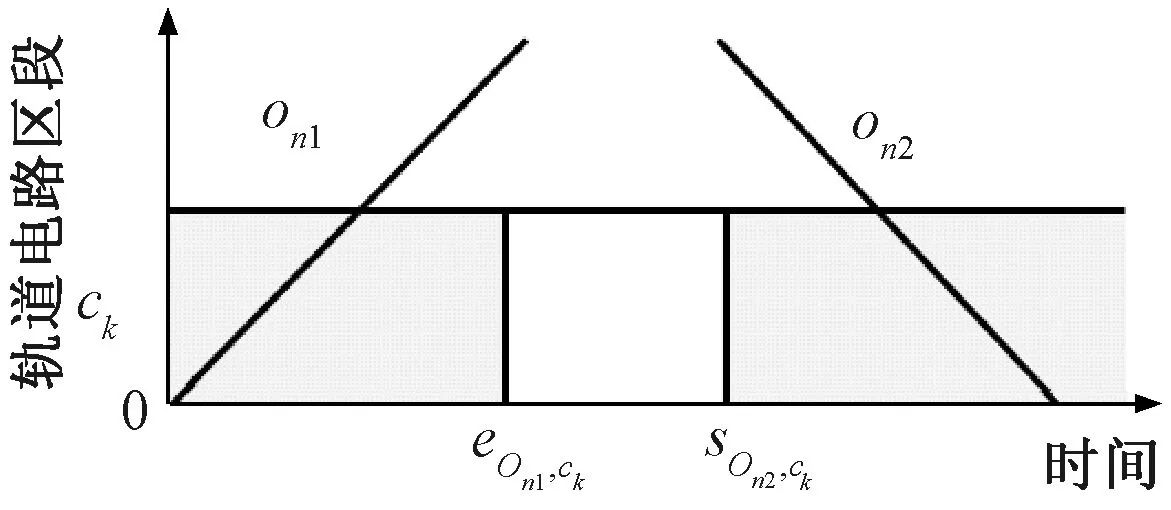
图5 咽喉区轨道电路区段占用情形1

图6 咽喉区轨道电路区段占用情形2
(5)到发线作业冲突疏解约束
∀pq1、pq2∈Pck∈Cpq1∩Cpq2∩CL
(15)
∀pq1、pq2∈Pck∈Cpq1∩Cpq2∩CL
(16)
∀pq1、pq2∈Pck∈Cpq1∩Cpq2∩CL
(17)
ck∈Cpq1∩Cpq2∩CL
(18)


图7 到发线轨道电路区段占用情形1
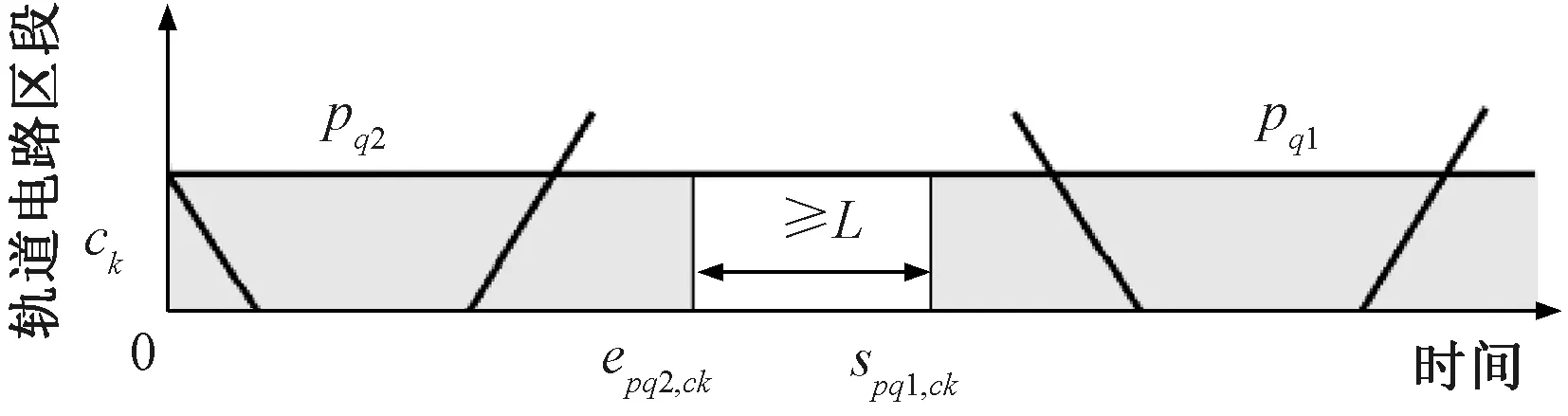
图8 到发线轨道电路区段占用情形2
(6)最小在站停留时间标准
toj-toi≥D∀(oi、oj)∈P
(19)
约束式(19)表示列车在站时间需要满足最短停留时间标准,保证旅客乘降等作业正常进行。
(7)区间追踪间隔约束
对于任意两项到达作业:
ton1-ton2+yon1,on2×M≥I
∀on1、on2∈OI
(20)
ton2-ton1+yon2,on1×M≥I
∀on1、on2∈OI
(21)
yon1,on2+yon2,on1=1
∀on1、on2∈OI
(22)
yon1,on2,yon2,on1∈{0,1}
∀on1、on2∈OI
(23)
对于任意两项出发作业:
ton1-ton2+yon1,on2×M≥I
∀on1、on2∈OJ
(24)
ton2-ton1+yon2,on1×M≥I
∀on1、on2∈OJ
(25)
yon1,on2+yon2,on1=1
∀on1、on2∈OJ
(26)
yon1,on2,yon2,on1∈{0,1}
∀on1、on2∈OJ
(27)
约束式(20)~式(27)表示任意两项到达(或出发)作业需要满足区间最小追踪运行时间要求,保证车站接、发的列车在区间高速运行不发生冲突。
(8)作业时刻调整
Ton≤ton≤Ton+Aonton∈N
∀on∈O
(28)
约束式(28)使得列车时刻能在一定的范围内优化调整,ton的下界为既有车站作业方案中作业时刻Ton,上界在下界的基础上添加一定的可调整时间Aon。不同列车可调整时间Aon不同,例如:相较于本线列车,跨线列车的可调整时间较小。
车站作业方案优化模型是整数规划模型,使用商业软件Gurobi求解。输入为车站作业方案中列车作业信息(车次、作业时刻上下界)、每项作业可以选择的进路集合和接、发作业连续关系,进路上轨道电路区段锁闭、解锁的时刻与列车作业发生时刻的差值。输出为包含所有列车作业时刻、走行进路及占用轨道电路区段时刻的车站作业方案。该作业方案合理配置咽喉和到发线的使用,是当前数量列车作业占用到发线时间最小的优化方案,缩短了列车占用到发线的时间,为到发线可用能力挖掘提供更多空间。
3 案例分析
北京南站分为普速场、京沪高速场、京津城际场,共设13座站台、24条股道,各场之间相对独立,专场专用,不存在跨线列车,因此北京南站的通过能力可以分场计算。本节以京津城际场为例,利用上述方法计算高峰时段通过能力。
3.1 基本数据
京津城际场设7条到发线,承担天津方向城际列车的始发终到作业,其东端咽喉轨道电路区段布置见图3,西端咽喉连接动车出入段线,不办理接发车作业。由图3可得列车进、出站基本进路集。
2019年4月10日调图后,京津城际基本运行图中,北京南站城际场每日始发终到249列,无通过列车。对于京津城际,文献[15]将08:00—11:00划分为客流高峰时段,该时段内列车集中到发,所有列车到站立折且采用“本线立折”的方式折返,无进出段作业,45项列车作业信息见表4。

表4 08:00—11:00间列车作业信息表
实地查定得到进路轨道区段锁闭、解锁时刻与列车作业时刻差值。表5为进路1(接车进路)上,以接车作业时刻为基准,反推得到的各轨道电路区段锁闭和解锁时刻,负号表示轨道电路区段锁闭时刻和解锁时刻早于接车作业时刻。表6为进路2(发车进路,与接车进路1对应同一条到发线)上,以发车作业时刻为基准的相关情况。其中,轨道电路区段22是到发线对应的轨道电路区段,其锁闭时刻由接车作业时刻决定(进路1),解锁时刻由发车作业时刻决定(进路2)。
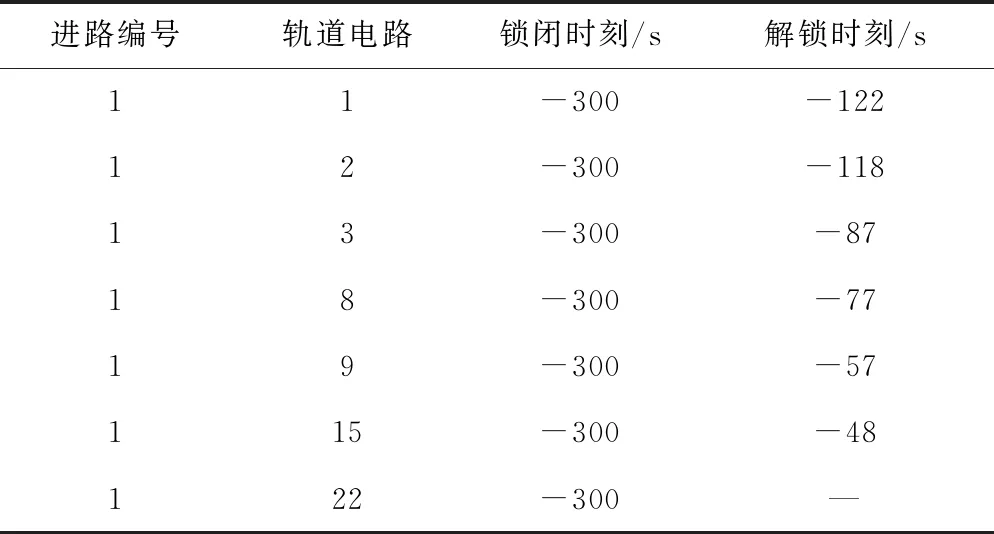
表5 进路1轨道电路区段锁闭、解锁时刻数据

表6 进路2轨道电路区段锁闭、解锁时刻数据
3.2 案例求解分析
为了保证高峰时段能力计算的准确性,避免时段开始和结束时能力损失,将研究时间窗适当拓展为[07:30,11:30],输入初始的作业信息建立车站作业方案优化模型,统计时段[08:00,11:00]的列车信息。由于该时段京津城际场办理的均为“本线立折”列车,因此,基于上述车站通过能力计算方法每次添加1列“本线立折”列车,即在车站作业方案中添加一对连续的接、发车作业。考虑到该场办理的列车多为天津方向的城际列车,具有同质性,列车顺序的调整对于运输任务影响不大,可以设定既有车站作业方案中的列车可调整时间为1 h。
3.2.1 能力计算与分析
使用C#编程语言调用Gurobi V8.1.1求解,运行环境为台式计算机(Inter(R) Core(TM) i7-9750 H CPU @ 2.60 GHz 2.59 GHz处理器,8 GB内存),得到接发列车数与目标函数值的关系见图9。
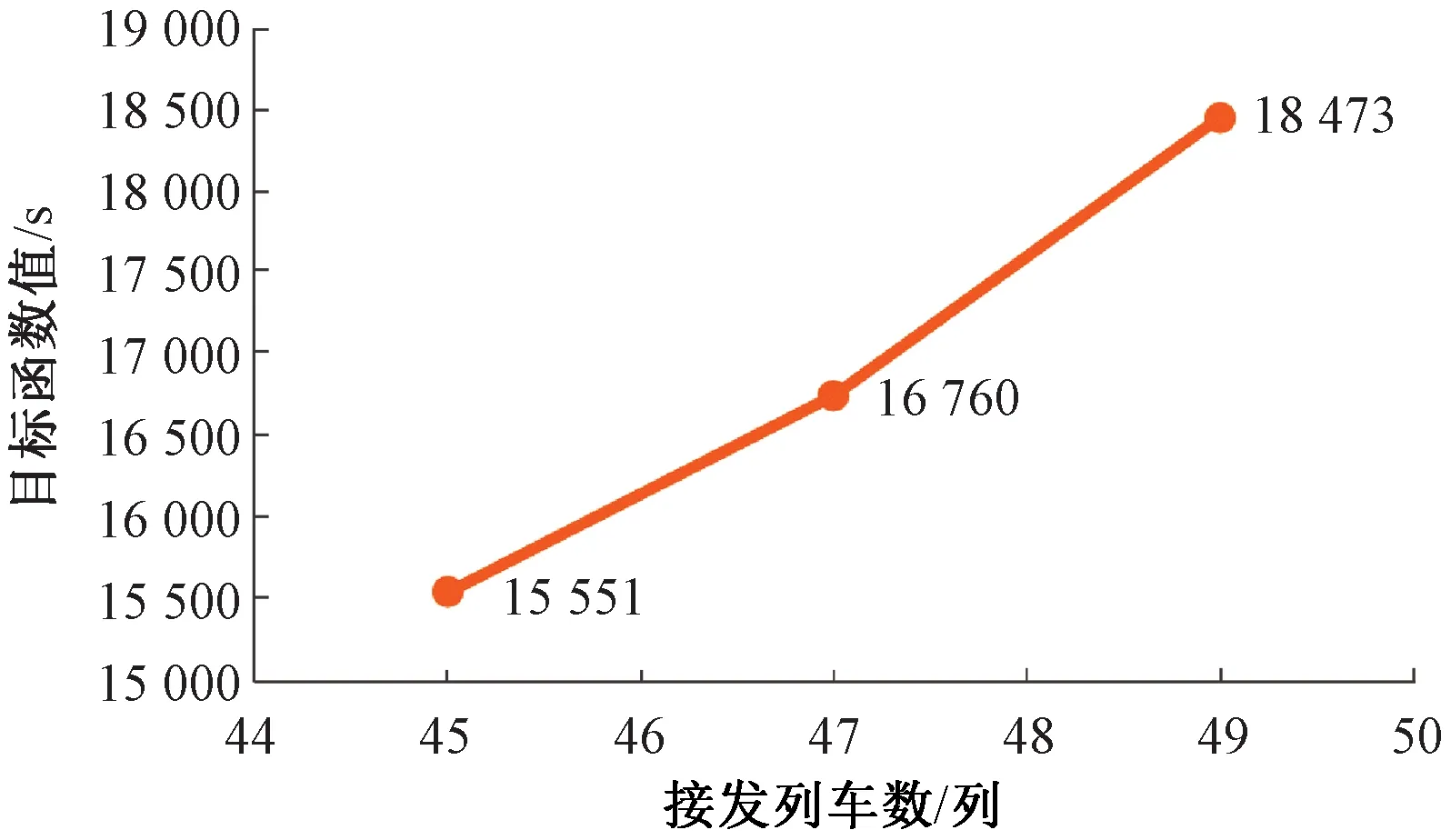
图9 接发列车数与目标函数值的关系
由图9可知,接发列车数与目标函数值正线性相关。当列车数量达到49列后,无法再继续添加列车,当前的车站作业方案饱和,对应的饱和车站作业方案见图10。

图10 饱和的车站作业方案
以饱和的车站作业方案中的接发车数量作为京津城际场的通过能力,得到京津城际场3 h通过能力为49列(接车24列、发车25列),在既有车站作业方案列车数量基础上增加了4列(接车3列、发车1列)。从接发车数量上看,既有车站作业方案中,京津城际场的能力利用率已达91.8%。
根据饱和的车站作业方案,可以计算得到咽喉区、到发线轨道电路区段利用率见图11。

图11 轨道电路区段利用率
由图11可知,在饱和车站作业方案中,到发线轨道电路区段利用率较低,普遍位于50%以下,到发线能力存在损失。而咽喉轨道电路区段整体利用率相对较高。其中,轨道电路区段4利用率高达70%,是6、7道接车,车站发车作业必经之处,是京津城际场接发列车的瓶颈。另外,轨道电路区段5~9利用率也均超过60%,说明咽喉是制约京津城际场通过能力的主要因素。
3.2.2 特殊作业对能力的影响
上述案例的求解中没有考虑特殊作业,如上水、吸污等。对于枢纽站而言,这些作业设备一般设置在特定的股道,作业时间也较为不同。这里以吸污作业为例简述特殊作业对通过能力的影响。假定有两列立即折返列车需要在6道进行吸污作业,并规定吸污作业占用到发线的最短时间为20 min。
利用通过能力计算方法,可以得到这种情形下车站作业方案饱和时目标函数为17 158 s,相比不考虑特殊作业时的目标函数15 551 s(相同列车数量)增加了1 607 s,大于因吸污作业占用到发线的额外时间(960 s);在接发车数量上,安排吸污作业后,京津城际场3 h的通过能力为45列(接车22列、发车23列),与当前设备条件下最大接发车数量相比减少了4列(接车2列、发车2列),能力损失8.2%。
因此,对于大型枢纽站来说,特殊作业占用设备时间长、要求高,一定程度上会对咽喉作业产生交叉干扰,影响咽喉与到发线的协调配合,带来额外的资源损耗,是影响高铁车站通过能力的重要因素,因而不宜在高峰时段安排此类作业。
3.2.3 进路分段解锁对能力的影响
改变假设条件,在不考虑进路分段解锁的条件下,更新进路上轨道电路区段锁闭、解锁时刻与列车作业发生时刻的差值,求解得到这种情形下车站作业方案饱和时目标函数为14 107 s,京津城际场3 h内接发车数量为40列(接车20列、发车20列),与当前实际的车站作业方案接发45列车相比,减少了5列车(接车1列、发车4列),尚不能满足当前车站作业方案的开行需求。由此可知,采用进路分段解锁可以有效地提高车站的通过能力,这是与实际情况相吻合的。因此,该研究结果表明,考虑分段解锁后,由于车站作业刻画更为精细,能力计算结果更加准确。
4 结论
依据图解法铺画“饱和车站作业方案”以计算车站通过能力的思想,本文考虑进路分段解锁提出了基于高铁车站作业方案优化模型的高铁车站高峰时段通过能力计算方法,并以北京南站作为案例进行了分析验证。
案例计算结果表明,该方法的优势在于:①综合考虑咽喉和到发线的关系,使得通过能力计算更加符合实际;②考虑进路分段解锁,使得通过能力计算更加准确;③能够给出能力利用最优的车站作业方案,可作为能力利用状况的评估依据,或用于指导实际的车站作业方案编制工作。此外,可以进一步拓展该方法,使之可以处理更多类型的列车作业,以适应所有时段车站通过能力的计算。然而调用Gurobi求解模型时,其分支定界效率一定程度上会影响求解速度,不适用于计算大规模问题。因此,还需对模型算法效率进行深入研究。

