倾角对含内热源封闭方腔内湍流自然对流换热影响

马兵善，王 烨，赵兴杰

(1. 兰州交通大学 环境与市政工程学院，兰州 730070；2. 兰州理工大学 土木工程学院，兰州 730050；3.兰州交通大学 铁道车辆热工教育部重点实验室，兰州 730070)

在实际工业工程中，如建筑热环境、电子元器件的冷却、太阳能集热器等方面均存在湍流自然对流现象.为深入理解其传热机理，许多学者进行了大量的研究[1-3].早期的研究经历了从纯自然对流换热到考虑壁面辐射效应对换热特性的影响过程[4-5]，后来发展到同时考虑壁面辐射和内热源条件下的封闭腔内湍流自然对流换热研究[6-7].Kuznetsov等[8]采用类似直接数值计算的方法，对局部辐射板加热的封闭腔内复杂传热(湍流自然对流、导热和表面热辐射)机制进行了研究.Miroshnichenko等[9]对水平放置、上下底面绝热、含有内热源的封闭腔内的复杂传热的研究发现：热源表面的对流努塞尔数是表面发射率的减函数，壁面辐射有利于腔内的传热过程.Miroshnichenko等[10]对水平放置含内热源的封闭腔内湍流自然对流——壁面热辐射进行了数值研究，发现壁面发射率使壁面平均总努塞尔数增大，热源位置引起了腔体内流动方式和热羽流的显著改变.Miroshnichenko和Sheremet[11]对内热源位于底面中心的倾斜方腔内存在壁面热辐射的湍流自然对流进行了数值分析，发现热源表面辐射努塞尔数随着腔体倾角的增大而减小.Sivaraj等[12]对中央放置方形等热流源的倾斜方腔内壁面辐射——自然对流耦合传热进行了参数研究，发现热源表面的平均对流努塞尔数是关于倾角的减函数，而且，不同壁面发射率所得热源表面平均对流努塞尔数随倾角的变化趋势一致.但这些研究的局限性或者是其单一的边界条件或者是热源位置固定，与工程实际存在较大差异.

实际工程中对封闭空间内散热设备冷却问题进行优化设计时往往要考虑多种边界条件作用下的耦合传热过程，其中，冷却效果与散热设备的位置及安装角度密切相关.同时考虑腔体倾角、内热源位置以及辐射效应对腔内对流换热特性影响的文献，目前还未见报道.基于这一研究现状，为了获得含内热源封闭腔内的传热特性和最佳对流冷却效果，本文对不同倾角下的封闭腔内自然对流换热过程进行了数值分析，旨在揭示复杂条件下封闭腔内自然对流换热机制，为改善工程实际中的对流冷却效果提供理论参考.

1 物理模型和数学模型

1.1 物理模型

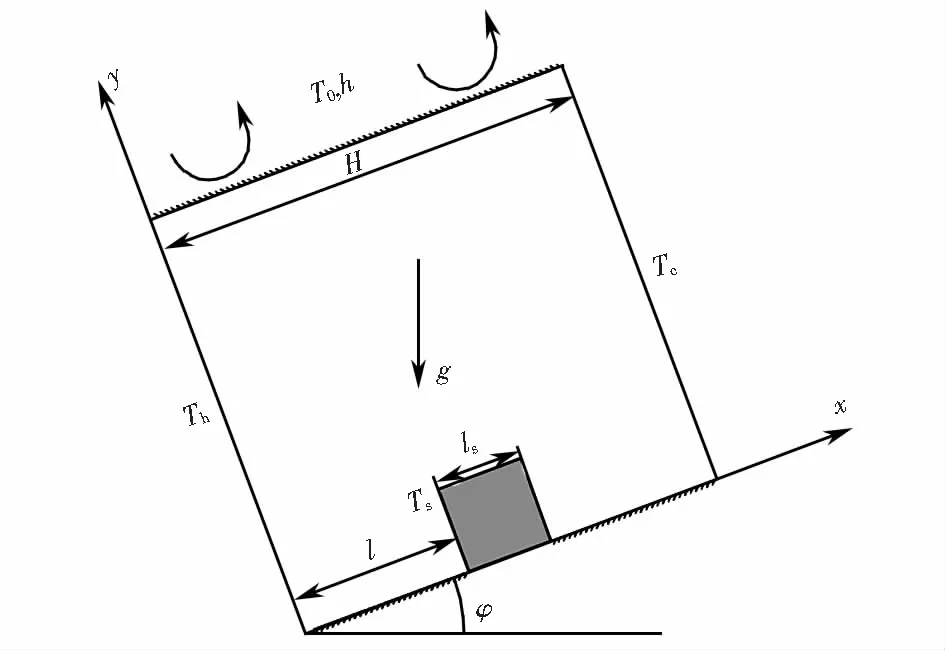
图1 物理模型Fig.1 Physical model

1.2 数学模型

用于求解流动与传热的控制方程如下：

连续性方程：

·V=0,

(1)

动量方程：

(2)

(3)

能量方程：

(4)

湍流动能k方程：

(5)

湍流动能耗散率ε方程：

(6)

上式中，t为时间s；T为温度K；T0为参考温度，K；p为压力Pa；u，v分别为x、y方向的速度m/s；ρ为密度kg/m3；λ为导热系数W/(m·K)；cp为定压比热容J/(kg·K)；μeff为有效湍流黏度；β为热膨胀系数K-1；φ为腔体的倾角°.

DO辐射模型

(7)

边界条件：

热壁面温度恒为Th=323.15 K，冷壁面温度恒为Tc=283.15 K，内热源表面温度恒为Ts=343.15 K，外界环境温度T0=(Th+Tc)/2，外界与腔体外壁面间的对流换热系数为h=7 W/(m2·K)[13]，所有气固交界面均为速度无滑移边界条件.

腔体中热壁面的局部对流努塞尔数Nuconv和局部辐射努塞尔数Nurad分别定义如下：

(8)

(9)

其中：qconv为壁面的对流热流密度，W/m2；qrad为离开壁面的净辐射热流密度，W/m2；ΔT为计算温差；H为特征长度.

几何平均努塞尔数：

(10)

(11)

总平均努塞尔数：

(12)

2 数值方法

利用SIMPLE算法对所研究问题的控制方程进行求解，采用非均分交错网格.对流项采用QUICK格式，扩散项采用中心差分格式进行离散.为了验证算法的正确性，对文献[14]所研究的方腔内湍流自然对流问题进行了数值计算.计算结果如图2所示，腔体Y=0.5水平线上无量纲垂直速度和无量纲温度与文献[14]中的实验数据符合较好，因此，该方法可用于后续计算.对于本文所研究的问题，为了获得网格无关解，分别采用网格数为150×150、200×200、250×250、300×300的四套网格进行了数值试验，得到了如图3所示计算时长为500 s时腔体X=0.5截面上的水平方向上的速度分布.可以看出，不同网格数所得曲线吻合较好，认为本文模型可以获得网格无关解.考虑计算的经济性，后续计算中取网格数150×150，时间步长τ=0.05 s.

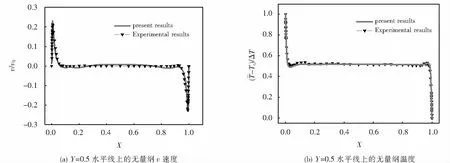
图2 数值方法验证Fig.2 Validation of the numerical method

3 计算结果及分析

对含内热源的倾斜方腔，为了研究腔体倾角φ、内热源距腔体热壁面的无量纲长度D(D=l/L)及腔体表面发射率对湍流自然对流的影响，计算中，Ra=1.58×109，Pr=0.71，倾角φ分别取0°、15°、30°、45°、60°、75°、90°，热源位置的无量纲长度D分别取0.1、0.2、0.3、0.4、0.5、0.6、0.7，壁面发射率分别取0、0.3、0.6、0.9.下面给出计算时长为t=1 000 s时的结果.

3.1 腔体倾角φ的影响

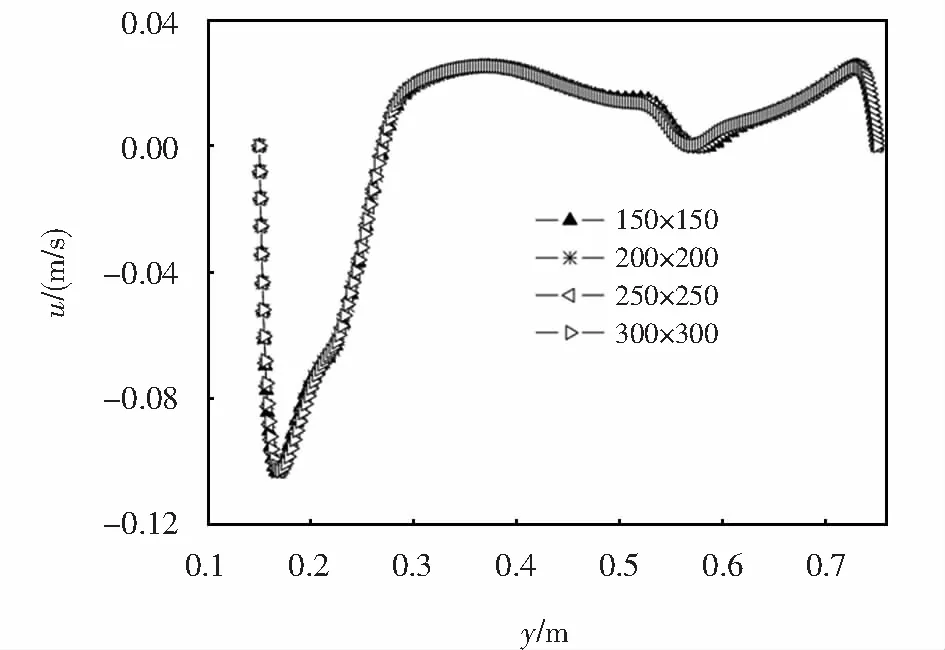
图3 网格独立性验证Fig.3 Validation of the mesh independence

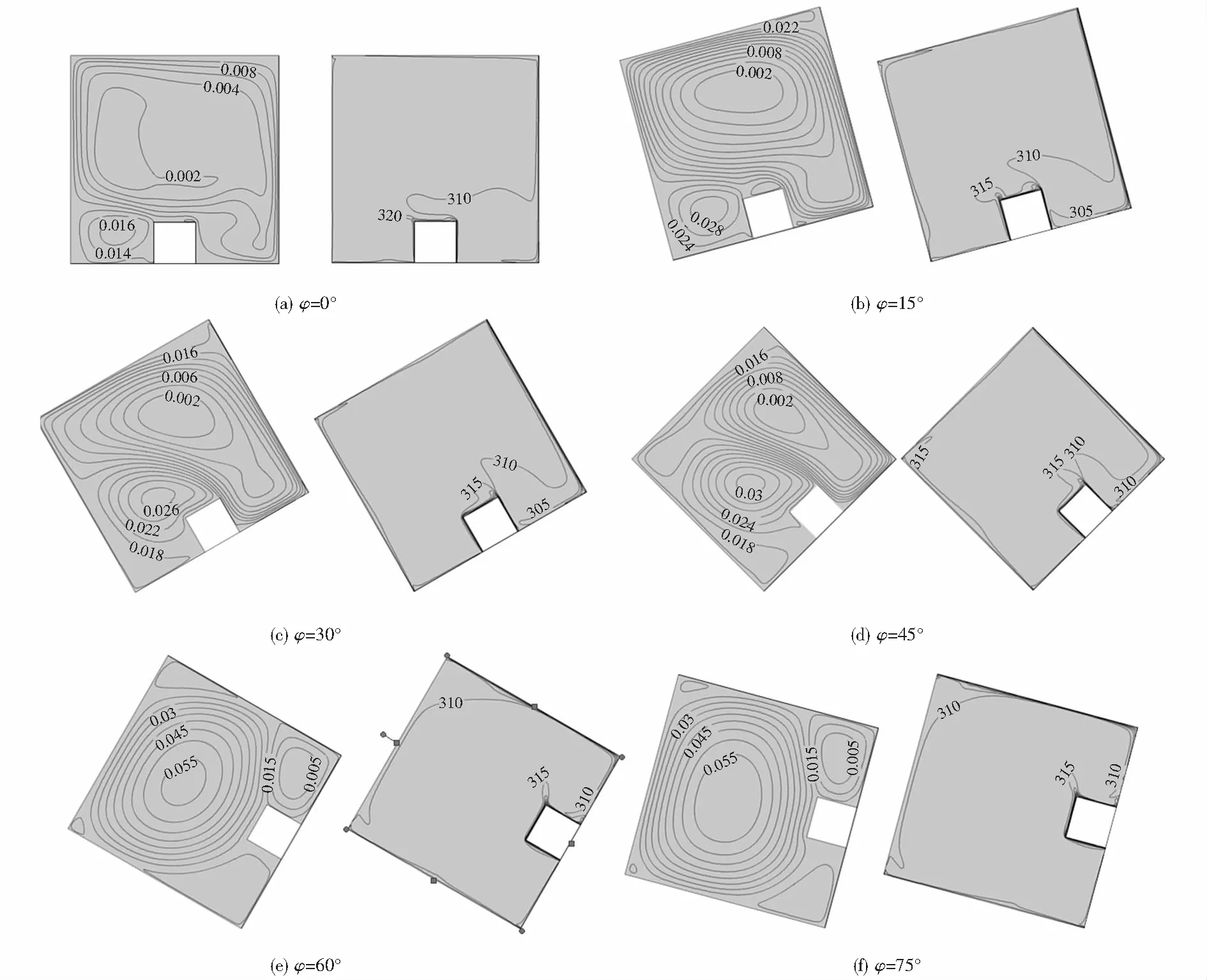
图4 不同φ时等流函数线(左)和等温线图(右)Fig.4 Streamlines(left) and isotherms(right) with φ 000 s)

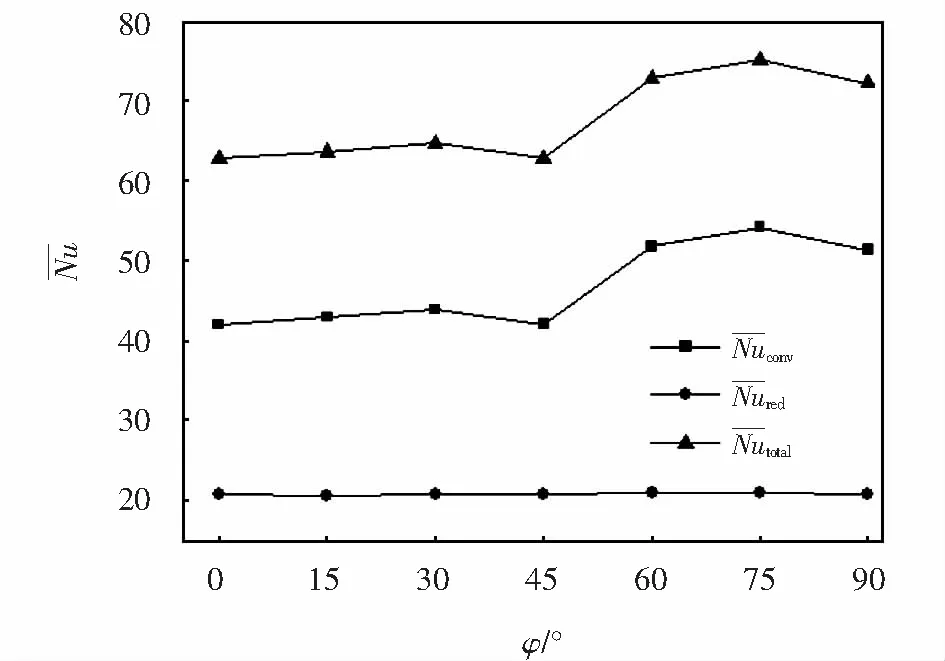
图5 热壁面平均努塞尔数随倾角的变化Fig.5 Variation of average Nusselt number on the hot wall with inclination angle

3.2 热源位置影响

由3.1节分析可知，腔体倾角为75°时对流冷却效果最佳.所以，下文只讨论腔体倾角为75°时的情况.

图6为φ=75°时不同无量纲长度D下的等流函数线图、等温线图、等湍流动能线图及等湍流动能耗散率线图.由图6(a)可以看出，腔体中心区域的温度变化对倾角变化不是很敏感，即保持了稳定的热层结构.当D=0.1时，在热源的上部顶角出现了热羽流，这主要是由于在浮升力的作用下，此处形成了两个反向旋转的涡，热羽流产生的位置在两涡的交界处.随着D的增大，热羽流向着冷壁面的方向扩展，是因为热源与冷壁面间的距离减小引起冷面附近的温度梯度增大，热源与冷壁面间的换热因此被强化.

图6(b)为腔体内的等流函数线的分布.腔体呈双涡结构，D=0.1时，左下侧逆时针旋转的涡相比于右上侧涡强度较大，但所占空间较小，主要是因为热源距离热壁面较近，受到热羽流的阻隔所导致.随着D增大，左侧涡所占腔体空间进一步扩展，成为主涡，D=0.2时取得最大流函数值，随着D的增大最大流函数值逐渐减小，是由于热源逐渐靠近冷壁面导致冷壁面附近流体在热源辐射作用下温度升高，浮升力减小，流动减弱.

图6(c)为腔体内湍流动能的等值线.D=0.1时，腔体内的湍流区域主要集中在热源的上部顶角和腔体的左侧，湍流动能的核心区与产生热羽流的位置一致.随着D的增大，湍流动能的核心向冷壁面方向转移，腔体中心区域的湍流动能变化较小，这与温度场结构有关.图6(d)为腔体中湍流动能耗散率的等值线图.D=0.1时，在热源上部顶角出现了一个涡结构，此处气流动能耗散较大，也正是两涡的交界面(6(b)所示)；D>0.3时，腔体中热源上方和热、冷壁面附近的湍流动能耗散率的梯度减小，说明腔体中的湍流强度减弱，流动变缓，腔体中热源位置对流动换热的影响显著.

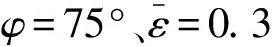
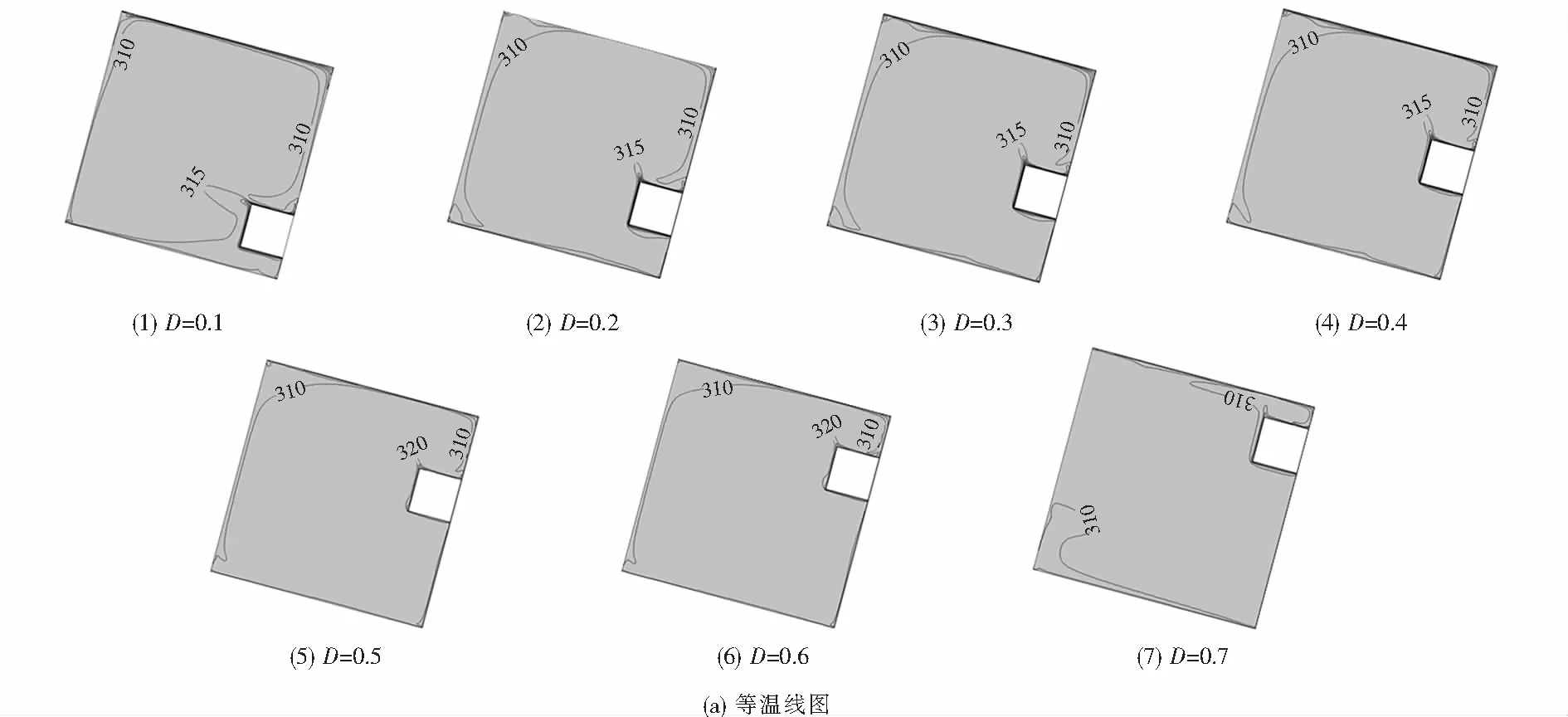
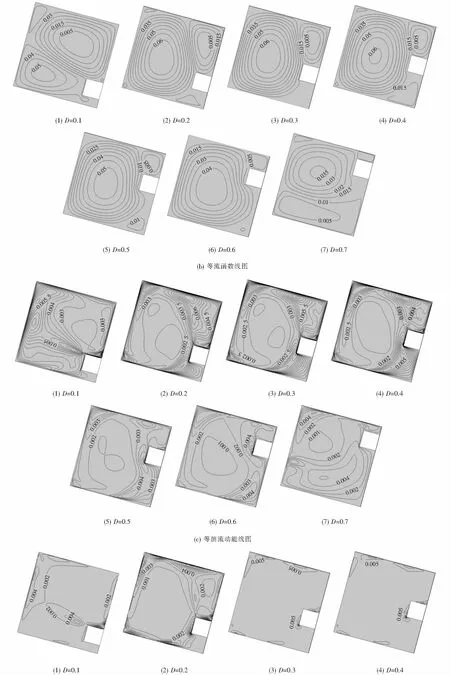
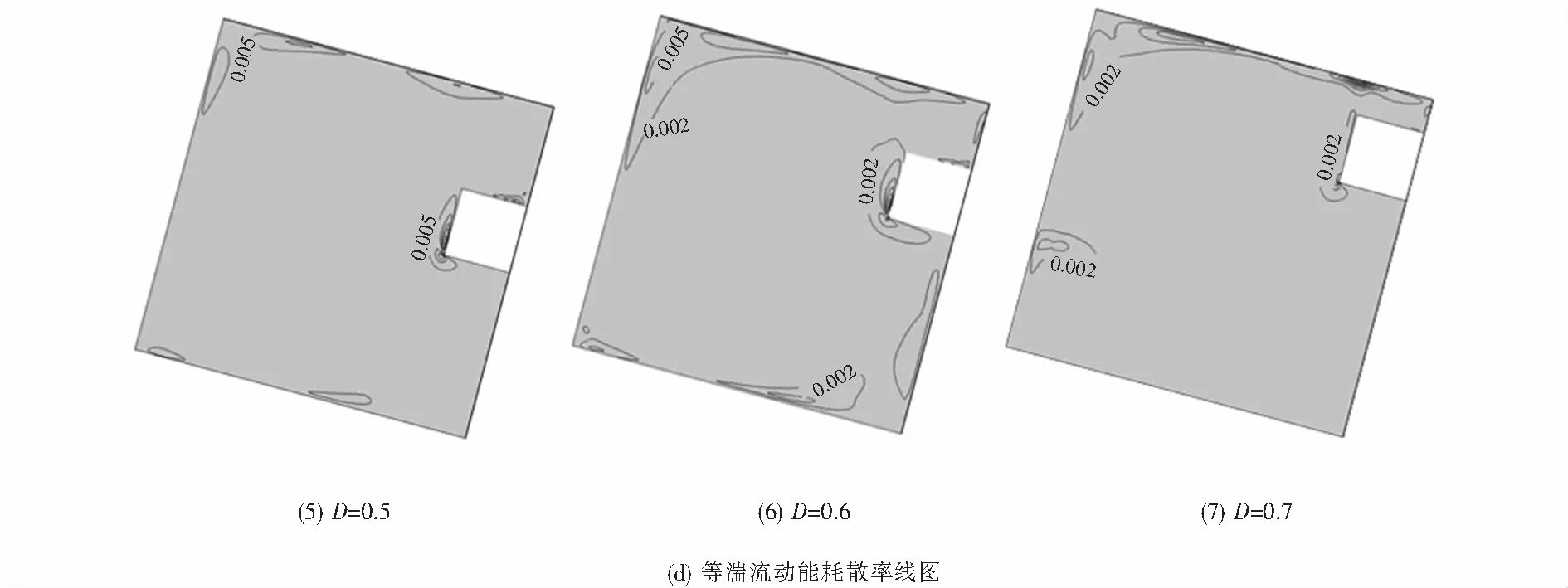
图6 (a)等温线图、(b)等流函数线、(c)等湍流动能线图和(d)湍流动能耗散率Fig.6 Isotherms (a),streamlines (b),turbulent kinetic energy fields(c) and turbulent kinetic energy dissipation rate field(d) at

如图7(b)所示，不同热源位置对腔内速度场分布影响显著.D=0.1时竖向速度在X=0.4处取得正的最大值，对应热羽流的形成位置；D=0.5时竖向速度在X=0.1处取得负的最大值.热源右移，热壁面附近流体被加速，这与图7(a)中热源右移有利于热壁面的冷却散热是一致的.0.2≤D≤0.6时热源位置对竖向速度的影响很微弱，这与图7(a)中温度场的分布特征一致，这一点体现了自然对流换热中温度场与速度场间的耦合关系.

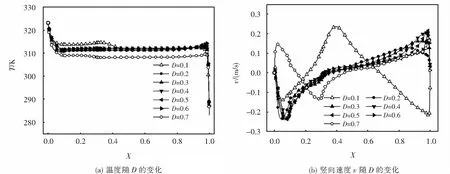
图7 Y=0.5水平线上温度和速度随D的变化Fig.7 Variations of temperature and vertical velocity with D at

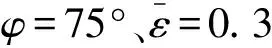
3.3 壁面发射率的影响

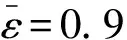
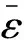
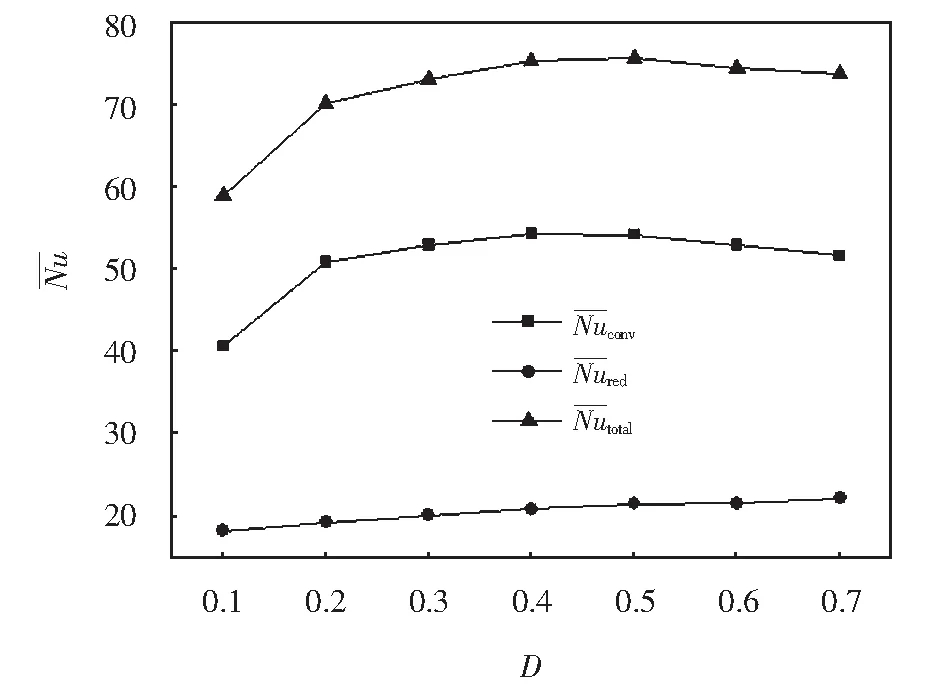
图8 热壁面随D的变化Fig.8 Variation of average Nusselt number on the hot

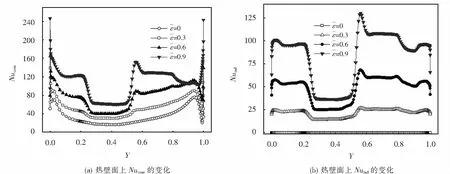
图9 热壁面Nuconv及Nurad随的变化(φ=75°，D=0.6)Fig.9 Variations of Nuconv and Nurad on the hot wall with at φ=75°,D=0.6

4 结论

对含内热源的倾斜封闭方腔内辐射—对流耦合传热特性进行了数值计算，得到了腔体倾角、热源位置及壁面发射率对湍流自然对流传热的影响规律，具体如下：

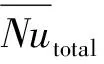
2) 辐射效应对总换热能力的贡献受腔体倾角的影响微弱，热源对热壁面冷却效果的贡献随其距热壁面无量纲长度D增大而增大.

3) 壁面发射率的增大对热壁面边界层起始段的对流换热以及辐射换热激励作用显著，较大的壁面发射率使得Y=0.5附近传热能力产生了阶跃性突增，但热边界层下游区域的辐射换热被削弱.