通信电子战干扰样式选择的博弈决策模型

赵禄达，王 斌,2，侯 嵬

(1.国防科技大学电子对抗学院，安徽 合肥 230037；2. 国防科技大学第三学科交叉中心，安徽 合肥 230037)

0 引言

现代战争中，电子战的作战双方总是处于对抗博弈的天平两端——电子进攻方的作战目标是干扰压制敌方所有电子目标，瘫痪敌方作战能力；电子防御方则需要综合运用抗干扰、反侦察、抗截获等多种手段和措施，对抗进攻方的干扰进攻[1]。从目前电子战与人工智能结合形成的认知电子战[2]来看，虽然电子干扰措施采取的是自适应策略，人工操作和干预较少，但是干扰决策的本质仍然是攻防双方的干扰-抗干扰策略博弈。所以，研究不同干扰样式下的电子战博弈策略就显得尤为重要了。

电子战中的干扰样式的决策分析始终是研究的热点。现阶段的静态干扰样式决策模型多是在没有电子进攻的静态条件下,以装备固有参数为主要参考的性能或能力评估模型，且考虑作战实际过程中的环境、人为因素较少。文献[3]提出了一种电子战干扰战术、技术措施相结合的博弈论决策框架，为后续研究做出了很好的铺垫。文献[4]在博弈论决策框架内将决策准则由最大最小值定理进行合理拓展，进一步提高了决策效率。文献[5]中引入博弈论对雷达的干扰效果进行了评估，虽然只是简单考虑了静态博弈的纳什均衡解，但展示出了将博弈论用于研究对抗效能的优势。近年来不少学者将人工智能运用到电子战决策中来，文献[6]总结了目前人工智能在电子战干扰决策方面的进展，提出了一种智能化干扰决策架构。文献[7—8]根据强化学习的框架，提出了电子干扰决策的自适应决策方法。

可以看出，目前的电子战干扰决策问题取得了较好的进展，但也存在以下几点问题：一是对雷达干扰样式选择的博弈和决策问题研究较多，对通信干扰样式的博弈和决策问题研究较少；二是在确定效用评价指标时，基本上均以误码率作为最终指标进行讨论，没有综合考虑通信电子战的系统因素、作战行动因素和指挥员主观因素等；三是在研究干扰决策的博弈过程时，以静态博弈为主，动态博弈的研究较少。本文针对以上问题，提出了通信电子战干扰样式选择的博弈决策模型，通过作战双方不完全信息的动态博弈解决了通信电子战行动决策中的干扰样式选择问题。

1 通信电子战干扰样式选择的博弈决策模型建立

通信电子战干扰样式选择的博弈模型由多指标评价模型和干扰样式动态博弈模型组成，如图1所示。首先在评价过程中，将不同性质的数据按照不同的数据预处理方法进行数据处理，基于改进AHP-熵权法对通信电子战作战效果指标权重进行确定；然后对不同性质的指标数据使用不同的聚合方法进行指标融合，从而得到系统评价指标；随后将系统的效用评价函数带入干扰样式博弈模型中，进行动态博弈分析；最后得到通信电子战系统干扰样式决策。

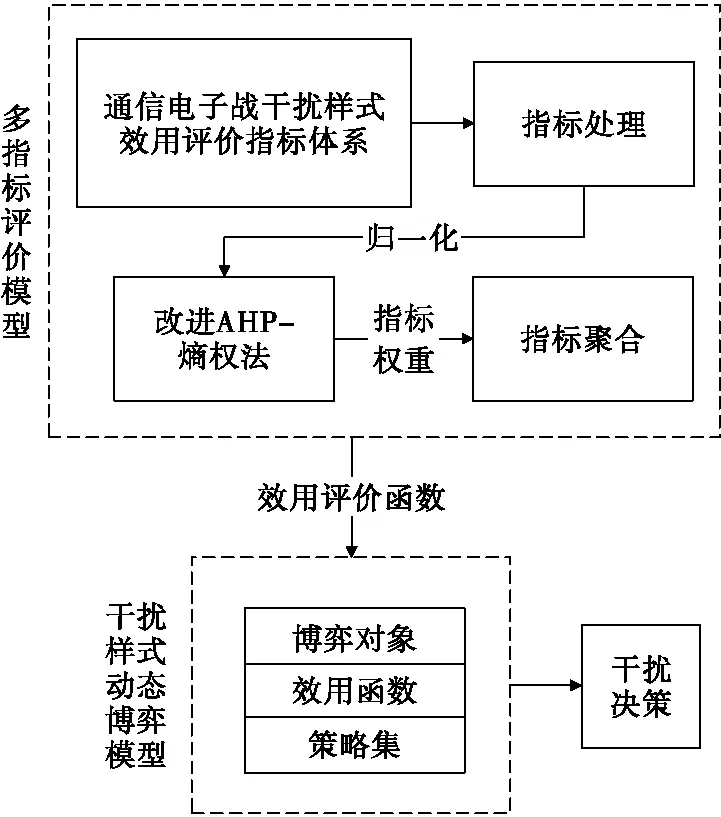
图1 通信电子战干扰样式选择的博弈模型示意图Fig.1 A illustration ofgame model for interference pattern selection of communication EW

2 基于多指标决策和动态博弈的干扰样式选择

2.1 通信电子战系统干扰效果多指标评价模型

如果综合考虑影响通信电子战最终决策的所有因素，就需要使用多属性决策评价方法来确定最终的效用评价函数，目前解决此类问题的方法有许多种，如灰关联评估法[9]、模糊综合评估法[10]和I2TOPSIS评估法[11]等。以上方法在评价过程中很少同时考虑攻防双方对抗博弈，对作战整体情况把握不足，且在指标处理时以线性处理的方法居多，对非线性指标的处理讨论较少。本文针对以上评价方法的不足，提出通信电子战系统作战效果多指标评价模型。

2.1.1干扰样式效用评价指标体系

指标体系结构如图2所示。指标体系主要由系统因素、行动因素和主观因素三部分构成，在末端状态层共有11个指标。其中，X11与X12两个指标属于定量指标，其余指标属于定性评价型指标。定性指标采取评语化打分法结合先验知识进行求解，下面将定量指标求解方法进行说明。

本文设定我方使用的通信电子战干扰信号样式有3种，分别为宽带噪声干扰(broad band noise, BBN)、部分频带噪声干扰(partial band noise, PBN)和单音干扰(single toner, ST)；敌方使用的通信抗干扰样式有2种，分别为：直接序列扩频通信(direct sequence spread spectrum, DSSS)和跳频扩频通信(frequency hopping spread spectrum, FHSS)。在我方3种干扰样式和敌方2种抗干扰样式的相互作用下的误码率求解方法可参见文献[12—13]。信号编码复杂度指干扰信号编码量与敌方通信网络信道规模的关系，一般在行动前进行确定，复杂度不宜过大或过小，由于这一指标在实际作战行动过程中变化不大，本文直接根据实例数据给出。

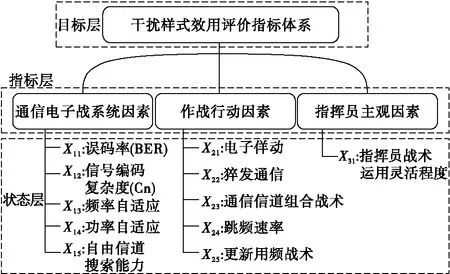
图2 干扰样式效用评价指标体系Fig.2 Interference pattern utility evaluation index system

在指标评价过程中给每个指标的重要性赋予一定的权重值，最后对不同性质的各个指标进行加权求和就可以得到最终的通信电子战系统效能评价指标。

2.1.2评价指标预处理方法

其次，对状态层的末端指标进行数据预处理。设指标归一化评语集为{c1,c2,…,cN}，其中c1为归一化评价指标的最差值，cN为归一化评价指标的最优值。

在图2建立的指标体系中，由于误码率取值一般采用分贝值表示，所以指标X11采用对数型指标归一化方法进行数据预处理。那么，第i个对数型评价指标归一化公式为：

(1)

式(1)中，imax、imin为第i个指标的最大最小值。

而通信编码的复杂度会随着编码数量的增加呈指数性增长，故指标X12采用指数型指标归一化方法进行数据预处理。那么，第i个指数型评价指标归一化公式为：

(2)

式(2)中，α、β为归一化参数，一般取值为2或3。

对于定性指标的评分描述，本文采用以下方式。

对第i个定性评价指标的评语描述为：

G(i)={(ci,χi),i=1,2,…,n}

(3)

式(3)中，χi为第i个指标隶属于第n个等级评语的可信度概率。则第i个定性评价指标的归一化评语描述为：

(4)

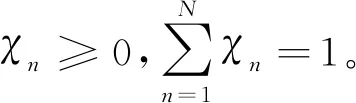
2.1.3使用改进AHP-熵权法确定指标权重

本文使用的改进AHP-熵权法确定指标权重包括三个部分，分别为使用改进的AHP法确定指标权重、使用熵权法确定指标权重和使用最小二乘法对确定好的两种权重值进行组合优化，算法框架如图3所示。

图3 干扰样式效用评价指标权重计算框架Fig.3 Calculation framework of index weight of interference utility assessment

下面对指标权重的求解方法分别进行说明。使用改进的AHP法确定指标权重的步骤如下：

1)根据图2构建的指标体系结构确定指标层次和每个层次的指标比较序号。

2)构建指标层与状态层的判断矩阵B1、B2，计算方法为：

B=(bij)n×n=bik/bkj

(5)

式(5)中，bij指的是标度i指标相对于j指标的重要性，计算方法为：

(6)

3)单层次排序并进行一致性检验。假设评价指标体系有k层，一致性指标CRk=CIk/RI。其中，RI为随机一致性比率，求解方式可参考文献[9]。CIk=(λmax-n)/n-1,λmax为矩阵最大特征值，若CRk<0.1，满足本层次的一致性要求，继续执行；若CRk≥0.1，则转到2)。

4)层次总排序并进行一致性检验。与3)类似，将CR=∑kCI/RI，若CR≥0.1，则转到1)修改层次结构模型和判断矩阵，若CR<0.1，满足总层次的一致性要求，输出最终层次排序uj，即为：

(7)

使用熵权法确定指标权重的步骤如下：

1)假设有n个评价目标，m个评价指标，将每个评价目标的评价指标数据放在一个矩阵中构成矩阵X，表示为：

(8)

2)确定每个指标的熵值。定义第j个评价指标的熵值为：

(9)

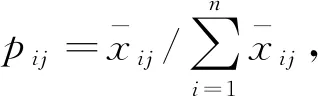
3)确定每个指标的权重。第j个指标的权重计算公式为：

(10)

使用最小二乘法对确定好的两种权重值进行组合优化的方法如下：

对于使用改进的AHP法和熵权法确定的两种指标权重理应相差越小越好，建立式(11)所示的组合权重的优化模型：

(11)

通过拉格朗日乘数法解得以上模型的解为：

(12)

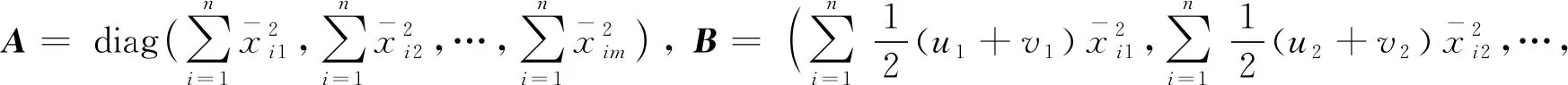
2.1.4指标聚合方法[14]

对于图2所示指标体系内的X13、X23、X24这3个指标，当其变化时通信电子战作战效果会随之产生非线性变化，而其余指标值在变化时上级指标基本呈线性变化。所以，在指标融合时，对于前一种指标类型采用加权平均算子(ordered weighted averaging,OWA) 进行融合，后一种指标类型采用加权几何平均算子(weighted geometric mean,WGM)进行融合，聚合方法分别为：

(13)

(14)

2.2 通信电子战系统干扰样式博弈模型

在以往的相关研究中，大部分的电子战系统的干扰决策是基于干扰反馈得出的[14]，并且假设干扰方采取的是比较固定的干扰方式，对电子目标的干扰顺序也是预先设定好的。主动的干扰样式的选择主要根据干扰行动前的预案实施，被动干扰样式的选择则是多通过以往的经验综合判断得出。此方式得出的电子战干扰决策主观性过强，随机性较大。现代智能化战争中，电子战的双方博弈行为已经不再仅仅是简单的利益冲突竞争关系，而是一种动态变化的环境和策略相结合的对抗过程。我方通信电子战系统对敌方通信网络实时侦察，敌方通信网络的目标信息在我方实时掌握的情况下，我方指挥员可进行战术判断并采取及时的干扰措施，而敌方在通信网络受到干扰后对我方使用的是何种干扰方式是未知的，加之双方的对抗行动也存在先后，那么，敌我双方的对抗行动可以视为一种不完全信息的动态博弈,攻防双方会根据最大化自身利益的原则来选择应对策略[15]。

本文建立的通信电子战系统干扰样式博弈模型的框架如图4所示。

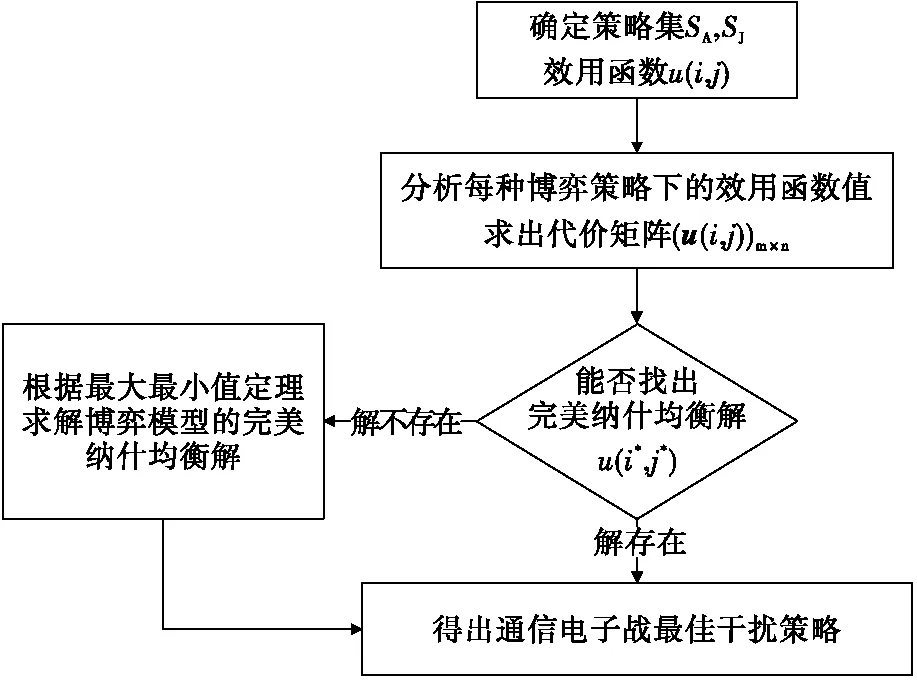
图4 通信电子战系统干扰样式博弈模型求解框架图Fig.4 Frame diagram of game model of jamming pattern in communication EW system

下面对模型求解步骤进行说明。

1) 确定博弈双方的效用函数和策略集。基于通信电子战效能影响因素结构，结合每个指标性质，构建出通信电子战系统效用值：

(15)

式(15)中，Ω={1,2,5,8,10,11}。以A表示通信方(敌)，J表示干扰方(我)，设敌方有p种通信抗干扰策略，我方有q种电子干扰策略，敌我双方的通信策略集为SA={A1，A2，…，Ap}，SJ={J1，J2，…，Jq}。

2) 选定盈利函数时，由于双方的零和对抗性，可以将同一函数作为双方的效用函数，唯一的区别是一方追求的是效用函数的最大化，而另一方追求的是效用函数的最小化，其博弈论表达式如下：

G={SA,SJ,UA,UJ}

(16)

式(16)中，UJ=-UA=U(SA,SJ)。

3) 在m×n种策略的对抗条件下，对得到的盈利矩阵使用最小最大优化方法[16]，在干扰效果最好的情况中选择最差的情况。在敌我双方提前未知双方策略的情况下，敌方盈利满足：

(17)

我方盈利函数满足：

(18)

下面考虑解盈利矩阵的两种情况：

①若VAi=VJj,对抗双方博弈平衡，得到纳什均衡解，此时Ai*,Jj*为对抗双方的博弈纯策略。

②若VAi≠VJj,对抗双方无法取得博弈平衡点，双方会以概率遍历所有策略，此时得到的稳定均衡解为对抗双方的混合策略的纳什均衡解。

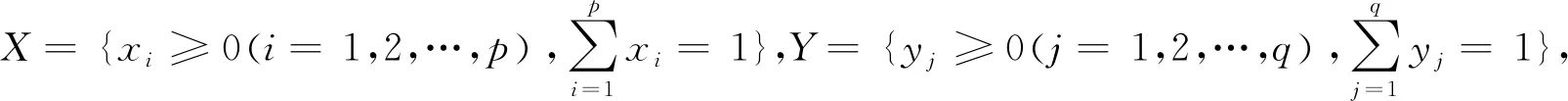
(19)

同样的，根据先最小后最大原理，当且仅当敌我双方的盈利与损失相等时，可得出混合策略下的纳什均衡解(X*,Y*)，即

(20)

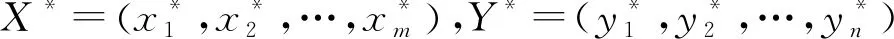
3 实例仿真与结果分析

3.1 仿真背景

本文仿真背景具体设置如下：假设某次电子战战术行动中，我方通信电子战系统对敌实施一次战术进攻，导致敌通信网络受到了干扰压制。敌方通信系统的信号调制方式为BPSK(二进制相移键控)，我方通信电子战系统对通信网络实施干扰压制。下文中设定3个模拟场景，场景中的通信系统指标仿真数据使用文献[17]中的实际数据均值代替，不同场景的指标仿真数据，如表1所示。

表1 3个不同场景下评价指标

我方行动集为SJ={J1,J2,J3}，敌方行动集为SA={A1,A2}，策略集为{(J1,J1), (J1,J2), (J1,J3), (J2,J1), (J2,J2), (J2,J3), (J3,J1), (J3,J2), (J3,J3)}，敌方策略集为{(A1,A1), (A1,A2), (A2,A1), (A2,A2)}。模型的评语集为{Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ}，对评语集相应评估范围进行拓展,得到{[0,0.01), [0.01,0.25), [0.25,0.5), [0.5,0.75), [0.75,1]}。

3.2 仿真步骤及结果

结合仿真背景使用本文建立模型进行算例仿真和结果验证，步骤如下：

1) 模型数据初始化。根据3.1节中3个场景的数据结合表1求解得出不同情况下的误码率。双方的效用值符号设置如表2所示。

表2 对抗双方效用值矩阵

2) 将仿真背景数据中的指标X11数据进行计算求解，得出3个场景的结果为：

根据干扰样式效用评价指标体系，对3个场景的数据指标进行计算融合，将处理后的3个场景数据带入评估模型中，即可得到每个场景总体评价效用值。在求解效用值时分别使用改进AHP-熵权法、改进的AHP法和熵权法将求得权重直接带入式(13)—式(15)求解得出的效用值与实际效用值进行比较，在3个场景中得到的结果如图5—图7所示。

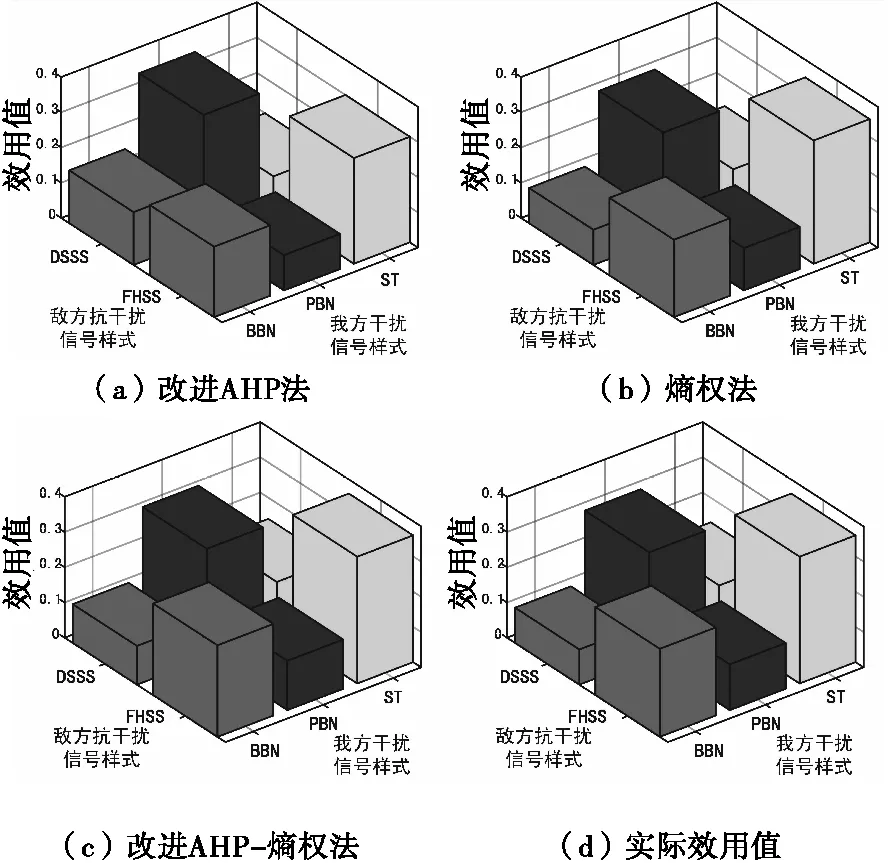
图5 场景1中使用3种权重确定方法得出的效用值与实际效用值Fig.5 The utility value and the actual utility value obtained from scheme 1 using the 3 weight determination methods

图6 场景2中使用3种权重确定方法得出的效用值与实际效用值Fig.6 The utility value and the actual utility value obtained from scheme 2 using the 3 weight determination methods

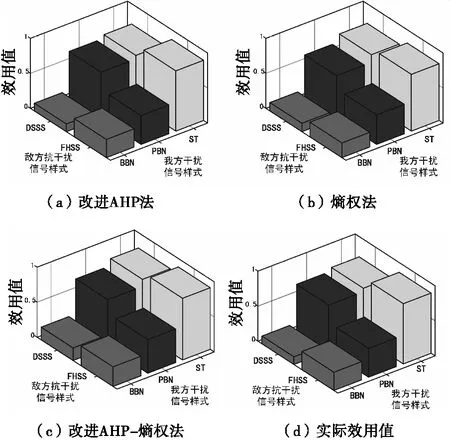
图7 场景3中使用3种权重确定方法得出的效用值与实际效用值Fig.7 The utility value and the actual utility value obtained from scheme 3 using the 3 weight determination methods

对以上3个场景使用3种不同方法求解得出的效用值与实际效用值的绝对误差进行比较，结果如图8所示。

图8 3个场景中3种不同方法得出的效用值与实际效用值之间的绝对误差Fig.8 Effective value of different strategies under fuzzy comprehensive evaluation

可以看出，使用改进AHP-熵权法求得指标权重进而求解的效用值与实际效用值之间的绝对误差要小于改进AHP法和熵权法，具有较好的稳定性。

3) 求双方盈利函数值(U(i,j))2×3。根据式(1)—式(3)中的求解方法结合式(15)的指标融合方法，结合步骤2)中求解得出的评价指标权重，即可求得3种场景下的敌我双方对抗博弈效用值矩阵，结果如表3所示。

4) 对抗决策求解。以场景1为例，通过场景的具体参数和敌我双方对抗态势，得出通信电子战干扰样式对抗博弈拓扑图关系如图9所示。

表3 对抗双方效用值矩阵

图9 博弈模型仿真拓扑图Fig.9 Model simulation topology

具体博弈求解流程如下：

①我方电子战指挥员首先根据战场态势情报和预先方案选定通信电子战系统内的3个类型的干扰样式的1种，敌方只能根据经验判断和先验知识采取防御措施。

②我方在选定了干扰样式的类型tk(k=1,2,3)后，对敌方实施通信干扰，对应的干扰方式表示为Jj(j=1,2,3)。

③敌方在发现通信网络受到干扰后，即可大致判定出我方干扰方式Jj，依据贝叶斯法则修正对我方干扰站类型的概率估计，有p=p(tk|Jj)，接着比较自己采取抗干扰行动A1、A2时的期望效用值：

(21)

确定效用值最大的行动A*(Jj)。当我方策略为(J2,J2)时，则我方的后验概率P{t1|J2}=P{t2|J2}=0.5，敌方观察后，采取A1时得出的期望效用值为P{t1|J2}×u(t1,J2,A1)+P{t2|J2}×u(t2,J2,A1)=0.5×(-3.2×10-2-7.5×10-4)=-0.016 4，使用A2时得出的效用值为P{t1|J2}×u(t1,J2,A2)+P{t2|J2}×u(t2,J2,A2)=0.5×(-1.0×10-1-1.9×10-2)=-0.006，显然此时应选用A2策略，对我方来说，效用值为U*=(u(t1,J2,A2),u(t2,J2,A2))=(0.01，0.019)。作为对比，求解另两组混合策略(J1,J1),(J3,J3)，得到敌方策略应为(A2,A2)。

④根据效益最大化原则，由下式

u(tk,Jj,A*(Jj))(k,j=1,2,3)

(22)

比较即可得出对我方最有利的干扰方式J*(tk)。将数据带入式(14)中得：

(23)

式(23)中，q1、q2含义解释见表4中备注的相关说明。计算得到的完美贝叶斯纳什均衡解为[((J2,J2),(A2,A2)),p=0.5,q1∈[0,1],q2≥0.513]即表示我方通信电子战指挥员选择类型1和类型2的干扰站后均会选择PBN作为干扰策略，敌方在观察我方干扰信号后做出贝叶斯判断，在我方前后两次干扰后选择FHSS抗干扰手段。

同理可得另外2个场景的博弈结果，经仿真计算，3个场景的完美贝叶斯纳什均衡解如表4所示。

表4 3个场景的完美贝叶斯纳什均衡解

表4中，P{t1|J2}=p,P{t2|J2}=1-p，P{t1|J1}=q1,P{t2|J1}=1-q1,P{t1|J3}=q2,P{t2|J3}=1-q2。

3.3 效用值选取仿真讨论

如本文引言中所述，目前在通信电子战系统的作战效果的评价研究中，大多数学者将误码率直接作为整个系统的效用函数[18]，但在实际作战中，战场环境的变化、指挥员策略的使用以及通信干扰信号样式的动态变化等因素，都会对结果产生影响。以本文仿真条件为背景，考虑3个场景不同对抗策略下的通信系统误码率随干信比变化的动态过程，仿真结果如图10所示。

图10 3个场景下不同对抗策略下的通信系统误码率随着干信比变化的动态过程Fig.10 The system SER varies with the J/S under different strategies of 3 scenes

可以看出，当敌方使用抗干扰通信手段为DSSS时，三个场景中的误码率随干信比的变化趋势基本一致，在我方使用BBN、PBN、ST三种通信干扰方式时曲线相互位置基本保持不变，且当敌我双方使用DSSS-ST对抗手段时误码率达到最高且相对稳定。这与表4中求解的完美贝叶斯纳什均衡解[((J3,J1),(A1,A2)),p=0,q1=1,q2=1]保持一致。但是，场景1中当敌方使用抗干扰通信样式为FHSS，我方使用BBN、PBN、ST三种不同的通信干扰方式时，误码率曲线并不一直处于相同大小关系的状态，在图10(d)中的Q1、Q2点左侧，使用FHSS-PBN对抗方式时的作战效果要始终优于使用FHSS-BBN对抗方式，而在Q1、Q2点右侧，双方使用FHSS-PBN对抗方式时的作战效果要始终劣于双方使用FHSS-BBN对抗方式。此时就需要电子战指挥员结合实际情况实施强力的战场干预，使博弈中的效用值函数始终处于利于我方的均衡状态。这也证明了仅仅使用误码率当做通信系统或通信电子战系统的效用值函数是不妥的，应采用本文建立的博弈模型进行预测求解。

4 结论

本文提出了通信电子战干扰样式选择的博弈决策模型。该模型在充分考虑实际作战中通信电子战的作战双方所面临实际情景的基础上，建立了综合考虑通信电子战系统因素、作战行动因素和指挥员主观因素的通信干扰样式决策评价指标体系，通过作战双方的不完全信息的动态博弈解决了通信电子战行动决策中的干扰样式选择问题。仿真实验结果表明，本文建立模型的效用函数比仅使用误码率作为效用函数更加符合实际要求，可以在对方决策信息未知的情况下对整个对抗过程进行预判分析，选择对自身效用最大的决策，对决策者的策略选择具有指导性价值。