无控弹丸刚体外弹道学应用综述

项 帆，王雨时，闻 泉，王光宇

(南京理工大学机械工程学院，江苏 南京 210094)

0 引言

刚体外弹道学在19世纪随着线膛火炮和圆柱形旋转弹丸的成功研制而诞生，属于刚体动力学，重点研究弹丸绕质心运动规律及其对质心运动的影响[1-2]。我国从20世纪60年代开始研究弹丸的绕质心运动[3]，包括弹丸的自转和攻角变化规律，然而受限于计算机仿真技术和气动力参数测试条件，无法给出刚体外弹道方程的数值解，只能通过实验测试其大致规律[4]。直到20世纪80年代，弹丸气动力参数测试方法成熟后[5]，刚体外弹道学模型才被应用到弹丸的飞行分析中。通过对弹丸刚体外弹道方程的数值解算，可定量分析弹丸刚体弹道诸元，从而在全弹道上准确判断出弹丸飞行稳定性。因此，刚体外弹道学是弹道诸元理论计算、外弹道设计、弹丸结构设计等方面的重要计算工具[6]。

目前，刚体外弹道学模型已日趋完善，其应用范围不再限于经典的弹道计算，在弹丸飞行故障查找、射击精度分析[7]、全弹实物仿真、大扰动条件下控制系统设计[8]、弹丸飞行落点预报[9-10]等方面都有涉及。本文简要介绍无控弹丸刚体外弹道学发展过程，对比分析准刚体外弹道学模型和刚体外弹道学模型差异，详细介绍旋转稳定弹丸和尾翼稳定弹丸的6自由度刚体运动方程，总结刚体外弹道学模型数值算法、气动力参数获取方式以及应用，试图为刚体外弹道学在引信技术中的应用特别是解决引信弹道炸问题提供参考。

1 刚体外弹道学发展概况

1.1 刚体外弹道学的特点和任务

无控弹丸外弹道学是研究无控弹丸在空气中运动规律及总体性能的科学，研究对象包括枪弹、炮弹、航空炸弹和火箭弹等“弹丸”(或“弹头”即飞行体)[11]，其最终目的是通过技术途径辅助这些“弹丸”更好地命中目标。目前，无控弹丸外弹道学在弹道计算、飞行稳定性评估、起始扰动分析、散布理论、总体优化设计、实验技术及参数辨识等研究领域都有应用[9]。

外弹道学可分为质点外弹道学和刚体外弹道学。质点外弹道学是在一定假设条件下，忽略对弹丸运动影响较小的一些力和全部力矩，把弹丸当成一个质点，研究其在重力、空气阻力和火箭推力作用下的运动规律。质点外弹道学的使命在于研究在此简化条件下的弹道计算问题，分析影响弹道的因素，并初步分析形成散布和射击误差的原因[12]。

刚体外弹道学则是考虑弹丸所受的所有力和力矩，把弹丸当作刚体研究其质心运动、围绕质心运动(亦称角运动)及其对质心运动的影响。弹丸的真实运动为6自由度的刚体运动，因此很多文献中也把刚体外弹道学模型称作6自由度刚体外弹道学模型[12](简称6D弹道模型)。一般认为刚体外弹道学的主要使命在于解释弹丸飞行中出现的各种复杂现象，研究弹丸稳定飞行条件、形成散布的机理以及减小散布的途径[13]，还可用于精确计算弹道[14]。

1.2 4D、5D弹道模型及其特点

在20世纪50年代人们就意识到在炮口处受到的扰动会使弹丸在外弹道上受多种力和力矩作用[15-16]，然而限于理论和实验条件，无法计算所有力和力矩；因此早期外弹道学模型是经过一定简化的，忽略了对弹丸飞行稳定性和射击精度影响较小的力和力矩。例如文献[13]在研究弹丸质心运动和绕质心运动时，就忽略了马格努斯力和马格努斯力矩。

此外，刚体外弹道学模型的初始参数和未知量比较多，其解算速度非常慢，无法满足实时性要求。通过适当减少对结果影响不大的未知量个数，可大幅度提升计算效率，这样简化后的刚体外弹道学模型称为准刚体外弹道学模型。按假设条件和气动力参数的不同，准刚体外弹道学模型分为4自由度外弹道学模型(简称4D弹道模型)和5自由度外弹道学模型(简称5D弹道模型)。

1.2.14D弹道模型

4D弹道模型由3自由度质点弹道模型改进而来，在其基础上增加了一个弹丸自转方程(即弹丸绕过质心的弹轴角运动方程)，从而在弹丸落点的侧偏中包含了因弹丸自转形成的偏流[17-18]。4D弹道模型中考虑了诱导阻力、升力、马格努斯力、极阻尼力矩和马格努斯力矩，并用动力平衡角(或者角运动稳态解)来代替攻角。4D弹道模型的作用是为了精确计算弹丸动力平衡角，并同时快速解算外弹道方程，其积分步长可达到1 s甚至数秒，且当全弹道上最大攻角较小时(2°～5°)，其解算结果较为接近6自由度刚体外弹道模型结果[19]。

4自由度旋转稳定弹丸的弹道计算，是Lieske最早(1966年)提出修正质点弹道模型，给出了平衡攻角方程[20]。应用该理论开发的4自由度外弹道计算软件(LOB和LOBS)大幅度改善了射击精度，目前在射表编制、炮兵火控系统中应用较为广泛[5]。

1.2.25D外弹道学模型

在较大射高的情况下，空气密度的影响使得弹重引起的攻角运动幅值增大，4D弹道模型在射程、偏流的计算结果上与6D弹道模型相差在1%以上[24]。因此需要在4D弹道模型和6D弹道模型之间找出一个折衷模型，既能改善4D弹道模型的结果又比6D弹道模型解算显著加快，由此推动了5D弹道模型的研究。

5D弹道模型又称为降6D弹道模型。在6D弹道模型中，弹轴运动可分为进动和章动。进动属于慢圆运动，章动属于快圆运动。5D弹道模型在计算旋转稳定弹的弹道时忽略了攻角运动中的快圆运动。对于无控弹丸而言，在外弹道上不会受到额外的扰动，此时攻角中的慢圆运动远远大于快圆运动，因而快圆运动对弹道的影响几乎完全可以忽略，反映在弹道方程上就是假设6D外弹道方程中的角加速度在弹轴坐标系y轴和z轴上投影为零[21]。

1.2.34D、5D弹道模型优点

相比于6D刚体外弹道学模型，准刚体外弹道学模型与质点外弹道学模型的差异在于外弹道方程的解算速度和精度。射高较小的情况下，在射角不是很大(小于65°)时，4D弹道模型、5D弹道模型和6D弹道模型的落点诸元几乎一致，而质点弹道方程则相差很大。当射高较大且射角也很大(大于65°)时，4D弹道模型相比于5D弹道模型和6D弹道模型会产生一定偏差[22]。

在计算速度上，质点弹道模型最快，6D弹道模型最慢。若以2自由度外弹道学模型(后面简称2D弹道模型)为标准，则6D弹道模型解算时间是2D弹道模型的数百倍，5D弹道模型是2D弹道模型的几十倍，4D弹道模型解算时间是2D弹道模型的2～3倍[23]。

文献[24]以155 mm口径低阻远程底排弹为例，在初速795 m/s、射角72°、最大攻角28°、计算机为IBM/PC XT条件下，对比4D弹道模型、5D弹道模型和6D弹道模型的解算结果，见表1。

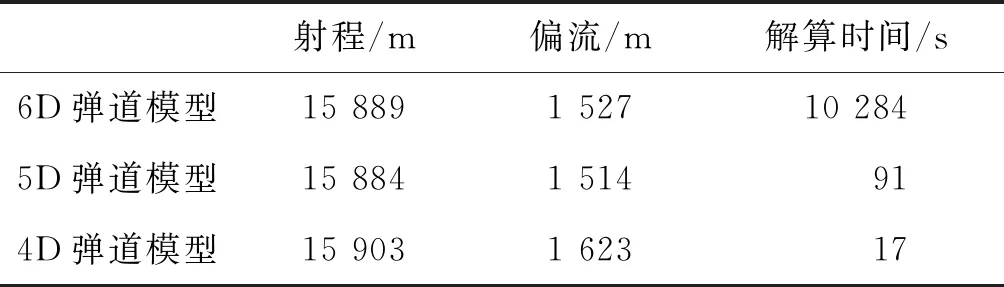
表1 不同弹道模型对155 mm口径低阻远程底排弹计算结果

由表1可以看出，4D弹道模型计算速度最快，但是在偏流上与6D弹道模型误差较大，而5D弹道模型在4D弹道模型和6D弹道模型之间做了很好的折中，在精度上与6D弹道模型相比误差小于1%，在时间上仅是4D弹道模型的5～6倍。

1.3 刚体外弹道学模型

1.3.1基本假设

6D弹道模型考虑了弹丸外形尺寸。对于常规火炮弹丸，其射击距离和飞行高度有限，可忽略地球曲率的影响，也可不考虑高度对弹丸重力的影响[25]。一般有如下基本假设：

1) 气象条件为标准气象条件；

2) 地表面是平面，重力加速度恒定，方向垂直向下；

3) 忽略地球自转产生的科氏惯性力；

4) 不考虑气动烧蚀[26]；

5) 弹丸质量分布均匀[27]；

6) 弹丸是轴对称体，即关于纵轴对称。

1.3.2基本坐标系

刚体外弹道学重点研究弹丸绕质心的旋转运动，然而其弹轴摆动规律和自转规律不易在地面坐标系中体现，因此需要建立其他坐标系。在以往的外弹道文献中，对弹丸绕质心运动规律是在速度坐标系、弹轴坐标系、弹体坐标系和第二弹轴坐标系中进行分析的。弹轴坐标系和速度坐标系由基准坐标系两次旋转而来，如图1和图2所示。弹体坐标系由弹轴坐标系绕弹轴旋转一个自转角得到，第二弹轴坐标系由速度坐标系两次旋转得到。

图1 速度坐标系与基准坐标系的关系Fig.1 The relationship between the speed coordinate system and the reference coordinate system

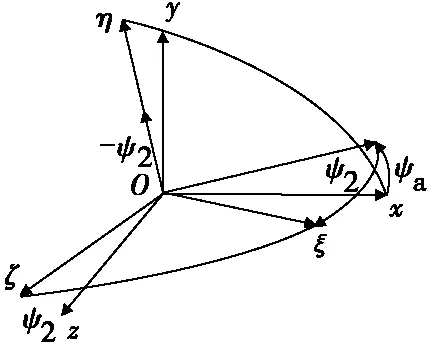
图2 弹轴坐标系与基准坐标系的关系Fig.2 The relationship between the bullet axis coordinate system and the reference coordinate system

弹丸6D外弹道学模型各坐标系之间的转换关系如图3所示。

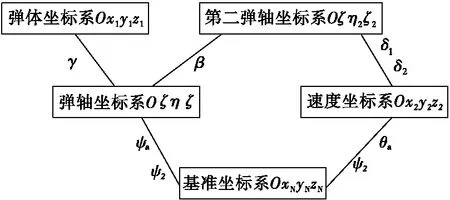
图3 弹丸6D外弹道学模型各坐标系转换关系Fig.3 Transformation relationship between coordinate systems of projectile 6D exterior ballistics model

1.3.3旋转弹刚体外弹道学模型

弹丸在外弹道上受到的力包括阻力、升力、重力和马格努斯力。其中，阻力方向与弹丸速度方向相反，升力垂直于速度方向向上，马格努斯力垂直于攻角平面。弹丸受到的力矩包括马格努斯力矩、极阻尼力矩、赤道阻尼力矩和翻转力矩。其中，马格努斯力矩垂直于弹轴，极阻尼力矩方向与转速方向相反，赤道阻尼力矩与摆动角速度方向相反，翻转力矩垂直于弹轴向上，用于保持弹丸平衡。图4为弹丸在外弹道上所受到的各种力和力矩[28-33]。其中Rx为阻力、Ry为升力，v为来流速度，xc为弹丸质心，xp为弹丸压力中心，δ为攻角，My为马格努斯力矩、Mxz为极阻尼力矩、Mz为翻转力矩、Mzz为赤道阻尼力矩。由弹丸运动和外弹道受力情况即可列出旋转稳定弹丸的外弹道刚体运动方程。

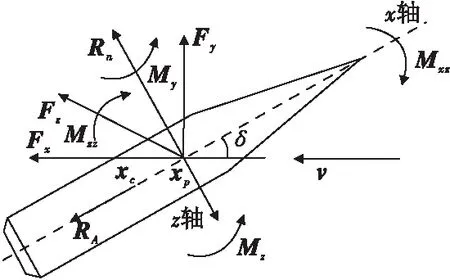
图4 旋转弹丸在外弹道上所受的力和力矩Fig.4 The force and moment of the rotating projectile on the outer trajectory

1.3.4尾翼弹刚体外弹道学模型

低速旋转的尾翼稳定弹在飞行过程中所受的力及力矩有：重力、升力、阻力、马格努斯力、稳定力矩、赤道阻尼力矩、马格努斯力矩以及尾翼稳定弹所特有的尾翼导转力矩。尾翼稳定弹丸在飞行过程中，基本不发生自转运动或者只有较低的转速，因此，在标准大气条件下其弹道弯曲是弹轴偏离速度方向的唯一根源[32]。

另外，如果弹丸低速旋转，则攻角的变化将不止是在平面内摆动，而是摆动和进动的综合运动。但经计算分析[34]，由于尾翼形成的控制力对弹丸的控制为末端控制，其进动运动非常小，故可以将其近似为平面内的摆动。

尾翼稳定弹刚体外弹道学模型通常有如下基本假设[35]：

1) 弹丸在纵向平面内运动，z坐标(侧偏)为零；

2) 弹丸发射时，扰动导致产生的初始攻角很小，在解算中假设为一小值。飞行中，稳定力矩和赤道阻尼力矩将使攻角作衰减的正弦振荡，直至稳定。在忽略攻角的振荡对速度矢量影响的前提下，所建立的攻角摆动方程与质心运动方程之间没有直接联系；

3) 弹丸不滚转，攻角只在所在平面内摆动，因而在模型中，只建立攻角所在平面内的方程，不需要分析其他分量。

在以上假设基础上可得尾翼稳定弹丸刚体外弹学道模型[36-37]。考虑到马格努斯力在合力中所占比例很小，而科氏惯性力仅对射程较远的弹丸才值得考虑，故尾翼稳定弹丸刚体外弹学道模型忽略了马格努斯力和科式惯性力[38-39]。

尾翼弹6D弹道模型应用很广：文献[40]用来分析尾翼稳定脱壳穿甲弹弹托的运动规律，对比了不同攻角、侧滑角条件下弹托的质心运动轨迹，揭示了弹托在分离过程中对弹丸的作用过程；文献[41]在分析地对地战术导弹再入速度时，应用6D弹道模型研究了尾翼子弹速度衰减规律，对比了不同初始弹道倾角、不同尾翼尺寸的子弹以及无尾翼子弹速度随高度变化规律；文献[42]在分析微型扰流片的控制机理和控制效果时，以尾翼弹为研究对象建立了考虑微型扰流片引起的力和力矩的6D弹道模型，解算并对比了不同初速、不同时刻打开扰流片时弹丸侧偏随距离变化规律。

1.4 刚体外弹道学模型求解

1.4.1刚体外弹道学模型解算初始条件

质点外弹道学模型只需要极少的初始参量(包括弹径、阻力系数、弹重、初速、射角)就可以得出弹丸的质心外弹道运动规律，而刚体外弹道学模型需要参量较多，分为三类：弹丸刚体模型参量、发射初始条件和弹丸气动力系数。

弹丸刚体模型参量包括：弹径、弹长、弹重、极转动惯量、赤道转动惯量、质心距弹底距离。发射初始条件包括：初速、炮口转速、射角、重力加速度、火炮缠度、初始章动角。外弹道气动力系数包括：零攻角阻力系数和存在一定攻角时的升力系数、马格努斯力系数、马格努斯力矩系数、翻转力矩系数、极阻尼力矩系数、赤道阻尼力矩系数。

1.4.2刚体外弹道学模型解算数值方法

常微分方程组的数值解法有：欧拉法、龙格-库塔法、阿当姆斯-预报矫正法和吉尔法等。欧拉法在计算机未发明之前应用较多，但不易满足精度要求；阿当姆斯-预报矫正法需要知道前三个函数值才能计算下一个函数值，因此在计算之前需要用其他方法(如龙格-库塔法)解出前三个函数值。用阿当姆斯-预报矫正法解算时只需要计算微分方程组右端函数值，能大幅度提升求解速度，但是不便于改变积分步长。对于刚性较严重的变系数、非线性、需变维以及初始值分段加入的常微分方程组的数值求解，可采用吉尔法。该方法容易改变阶和步长，且每积分一步解隐式方程组所需的工作量较小[43]。吉尔法缺点是计算复杂，有时引入的微分次数多。

求解外弹道方程最常用的数值方法是龙格-库塔法[44]。该方法是泰勒级数的改进版，是工程计算中广泛应用的高精度单步算法，适用于多数连续系统或离散系统。四阶龙格-库塔法能够满足6D刚体外弹道学模型解算的精度要求，其求解精度正比于积分步长的五次方。理论上积分步长越小精度越高，但积分误差会累积，因此积分步长也不宜过小[45]。龙格-库塔法易于程序化，在求解6D外弹道方程时运用最广的是四阶五阶龙格-库塔法，它用四阶方法提供候选解，五阶方法控制误差，是一种自适应步长(变步长)的常微分方程数值解法[46-47]。龙格-库塔法从诞生至今一直能在外弹道微分方程组求解上得到应用，在于以下优点:

1) 具有同一形式的计算流程图；

2) 不需要进行“起始”计算；

3) 计算过程中容易改变步长；

4) 能很好地适应方程右端函数为间断函数的情形。

龙格库塔法缺点也很明显，即不适用于刚性微分方程组的求解。文献[48]曾验证，龙格-库塔法不适用于未知数过多的刚性微分方程组求解，用龙格-库塔法求解战略导弹的6D弹道模型(包含数百个变量和数百个微分方程)时会出现严重病态现象，对这类弹道模型解算应采用高精度的龙格-库塔转阿当姆斯法以保证仿真精度，积分步长取为2 ms。

此外，吉尔法对解决刚性微分方程组有很高的稳定性，并且在同样的求解精度下求解时间最短，文献[49]对比了四阶龙格-库塔法和吉尔法在随机轨道模型(颗粒相模型)计算中的应用，发现吉尔法在计算稳定性和计算速度上显著优于四阶龙格-库塔法。目前还未发现吉尔法已经应用于无控弹丸刚体外弹道学模型解算。

1.4.3气动力参数获取

获取弹丸气动力参数的方式有四种：理论计算、实验测试、实弹射击和计算流体力学软件仿真。理论计算误差大，实弹射击成本高，目前很少单独采用。当前获取弹丸气动力参数的方式主要为实验测试和计算流体力学软件仿真。

实验测试包括靶道实验和风洞实验。靶道试验主要采用偏航纸靶和闪光阴影照相技术，获得的攻角精度为0.016°～ 0.12°，获得质心坐标精度为0.025～3 mm[50]。将靶道实验得到的数据通过概念-知识(C-K)技术[51]应用到弹道方程上，就可得出各气动力参数。风洞实验可以很好模拟弹丸在亚音速和跨音速阶段的气动力参数，能精确测量尾翼弹的俯仰力矩系数和偏航力矩系数[52]。

测试结果说服力较强，但受限于苛刻的实验条件和成本。目前更多的是使用计算流体力学软件仿真。计算流体力学方法具有易获取流场数据和成本低的优点，并且可模拟不同尺寸的物理模型，可较为精确地预测物理模型的流场特性及现象，在无法完成实验的情况下能够较为准确地得到模型的气动力参数[53]。文献[54—56]介绍了通过FLUENT流体力学软件仿真旋转弹和尾翼弹在不同马赫数下气动力参数的过程。对旋转稳定弹而言，仿真初始条件包括弹丸外形尺寸、飞行速度、空气密度和攻角。通过仿真可直接得到弹丸的阻力系数、升力系数、马格努斯力系数、翻转力矩系数、极阻尼力矩系数、赤道阻尼力矩系数、马格努斯力矩系数。

2 刚体外弹道学应用情况

2.1 刚体外弹道学在非引信技术领域的应用

刚体外弹道学在现代武器研制中已有应用，例如射表编制、火控系统设计、火炮测试与实验。伴随20世纪80年代后期外弹道实验技术快速发展，刚体外弹道学已应用于各弹种(末敏弹、弹道修正弹等智能弹药)的弹道特性分析，而不再局限于常规弹药领域。这些弹丸的弹道主要部分还是无控飞行，适合用刚体外弹道学模型进行分析[57]。目前刚体外弹道学在以下几个方面已投入使用或正在研究[48]：

1) 大扰动、大姿态偏差条件下的弹丸控制系统设计；

2) 飞行器系统质量评估和飞行落点预报；

3) 弹头再入段的误差分析；

4) 常规弹丸非常规飞行故障分析；

5) 导弹系统作战仿真和作战效能分析；

6) 弹道导弹精度分析和鉴定；

7) 基于6自由度的全弹道可视化仿真研究[58]。

2.1.1刚体外弹道学在射表编制中的应用

在现代战争对炮兵提出首发命中要求的情况下，提高射表精度并正确使用射表具有更加重要的意义[59]。在测试技术和计算工具不发达的过去，只能使用质点外弹道学模型编制射表。由于数学模型不精确，故编制射表要消耗大量弹药，而且编制周期很长，精度也不高。目前计算机技术已高速发展，可采用精度更高的6D弹道模型改进编制方法，尤其是对弹丸初始阶段，其攻角对弹道有很大影响，使用刚体外弹道学模型更为合适[28]。20世纪60年代初期，中国常规兵器试验中心曾尝试用6D弹道模型编制射表，后因耗用机时太长、占用容量太大、起始扰动无法给出等原因，以失败告终。1991年，我国就5D弹道模型编制射表的可行性作了进一步论证，在中国常规兵器试验中心太极-2220计算机上计算射角为65°、初速为700 m/s、射程为17 km的一条弹道约需机时88.45 s，而整个射表大约需要71 140条弹道，至少耗时296天，时间过长[60]。到目前为止尚未见有文献涉及起始扰动的确定问题。

一般射表编制是在标准气象条件下完成的。我国炮兵的射表形式参照了前华约射表[61]，是以低海拔靶场的实验结果为基础编制的。炮兵部队在高原使用过程中发现，采用这种方法编制的高原射表与实际存在明显差异。文献[62]给出了一种基于5自由度外弹道学模型的新型射表编制方法，并以155 mm口径底凹弹为例，分析其在高原环境下用传统方法(2D弹道模型)和新方法(5D弹道模型)编制的射表计算出的射程，见表2。从表2可看出，在射角为20°和50°、海拔1 423 m条件下，5D弹道模型比2D弹道模型的计算精度高很多。

表2 在高原环境下用2D弹道模型和5D弹道模型编制的射表计算结果比较[62]

2.1.2刚体外弹道学在火控系统中的应用

在火控系统中，火控弹道模型对火炮射击精度影响很大。火控弹道模型误差在火控系统所有误差中占比较大。对于地面火炮，距离误差占20%～50%，方向误差占15%～30%[2]。

随着测试手段和计算机技术的发展，火控系统弹道模型也在不断发展，相继出现了质点外弹道模型、修正质点外弹道模型、刚体外弹道模型和准刚体外弹道模型。一般形式的刚体外弹道模型计算时间过长，影响火控系统的反应时间。目前降阶的准刚体外弹道模型已可满足精度和实时性要求[63]，尤其是4D弹道模型，北约已把4D弹道模型作为射表和火控计算机数据处理的标准模型[61,64]。然而应用4D弹道模型迭代运算动力平衡角繁琐费时，而现代战争中为准确、快速地求解射击装定诸元和进行偏差修正，通常要求火炮计算机解算时间不超过5 s[65]。为此，文献[66]给出求解动力平衡角的另一种算法，称为快4D模型，与原算法相比计算结果精度不变，速度提升40%以上。

2.1.3刚体外弹道学在155 mm口径榴弹弹丸外弹道解算中的应用

目前，刚体外弹道学模型已应用在多种弹丸模型的外弹道计算中，其中以155 mm口径榴弹弹丸居多[67-70]。表3给出了几种155 mm口径榴弹弹丸模型初始参数，表4给出了三篇参考文献中155 mm口径榴弹弹丸模型6自由度弹道计算用气动力参数，弹1为底凹弹，其三维模型见文献[74]，弹2和弹3均为平底弹。

由表3和表4可知，155 mm口径榴弹弹丸气动力参数中零升阻力系数、升力系数、极阻尼力矩系数、翻转力矩系数相差不大，而马格努斯力系数和马格努斯力矩系数差异很大。在表3和表4给出的初始条件下，各模型计算射程和实验值见表5。由表5可知，马格努斯力系数和马格努斯力矩系数差异对计算误差影响不大，计算误差都在0.5%以内，远小于质点外弹道学射程误差。文献[72]分析了155 mm口径火炮榴弹弹丸地面密集度与射程的关系。表6和表7分别为155 mm口径榴弹弹丸在50°射角条件下地面密集度计算值与射表的误差对比以及不同射程下各因素(质量散布、初速散布、纵风散布、射角散布、横风散布和起始偏角)对地面密集度的影响。

表3 文献给出的三种155 mm口径榴弹弹丸刚体外弹道学模型初始参数

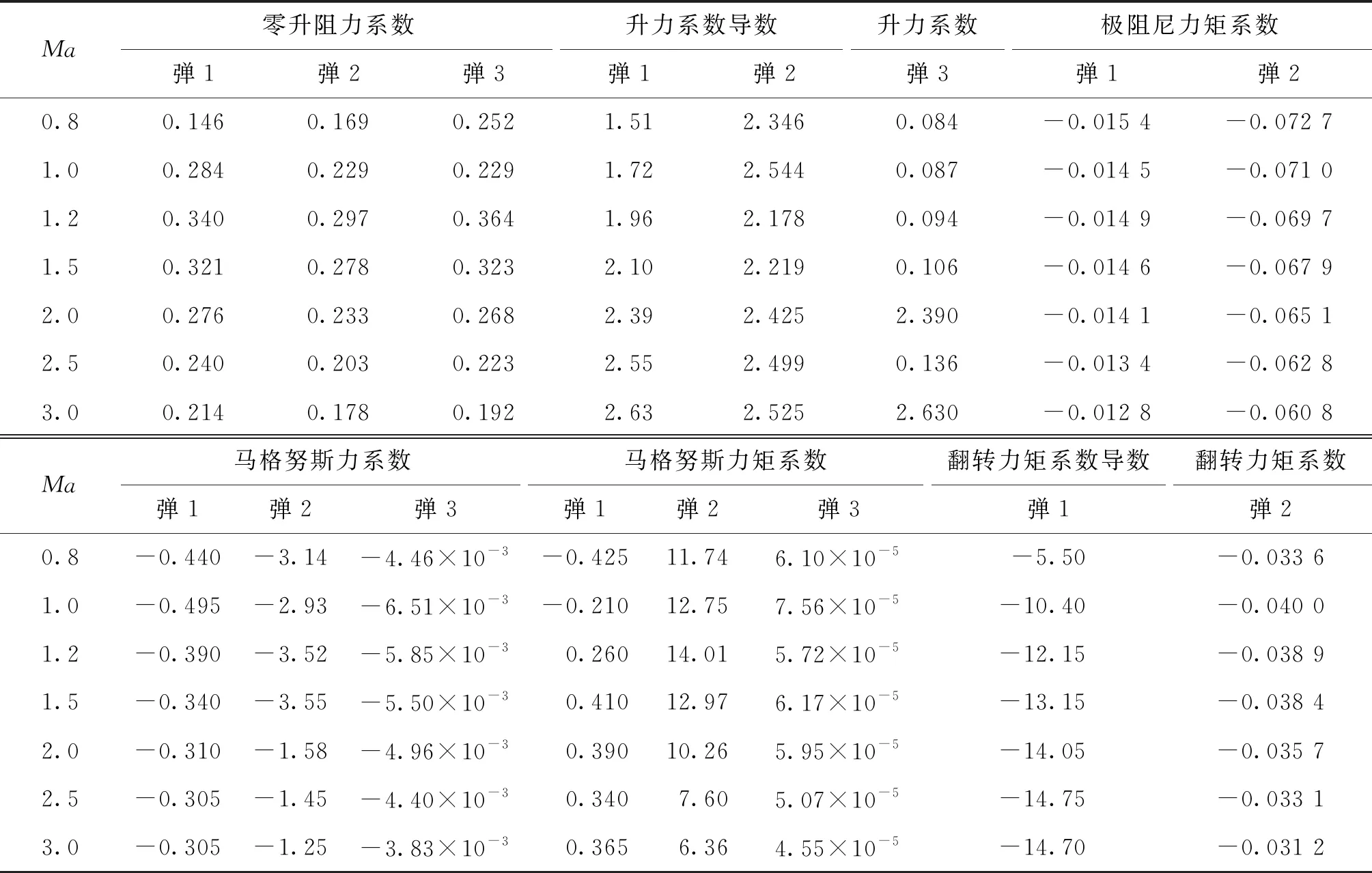
表4 文献给出的三种155 mm榴弹弹丸模型刚体外弹道学计算用气动力参数

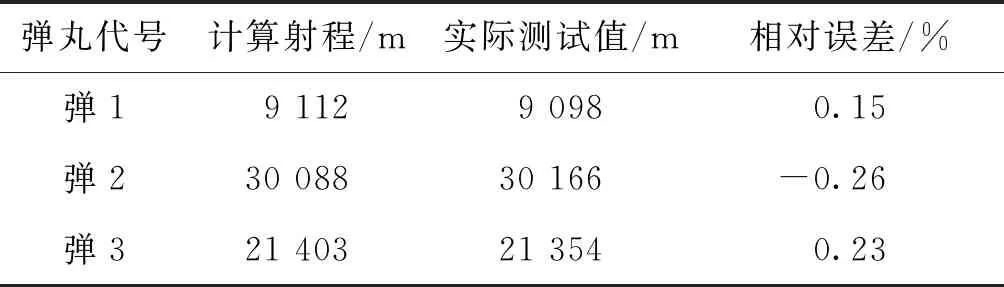
表5 文献给出的3种155 mm口径弹丸刚体外弹道学计算射程和对应测试值的误差[71-73]

表6 弹2在50°射角和30 088 m射程条件下地面密集度计算值与射表值[72]

表7 弹2在不同射程和不同射角条件下各因素对地面密集度影响[72]

文献[73]分析了考虑弹丸动不平衡时的弹丸6自由度外弹道方程(弹丸原始参数参考文献[73])，用其解算了155 mm弹丸(模型初始参数见表3和表4中的弹丸3数据)的飞行距离、高度、速度、速度高低角随时间的变化规律，并与质点外弹道学模型计算结果对比，如图5所示。可看出质点弹道模型和刚体弹道模型解算出的曲线在趋势上一致，但6D弹道模型比质点弹道模型计算出的射程、最大高度、落点速度和落角小。

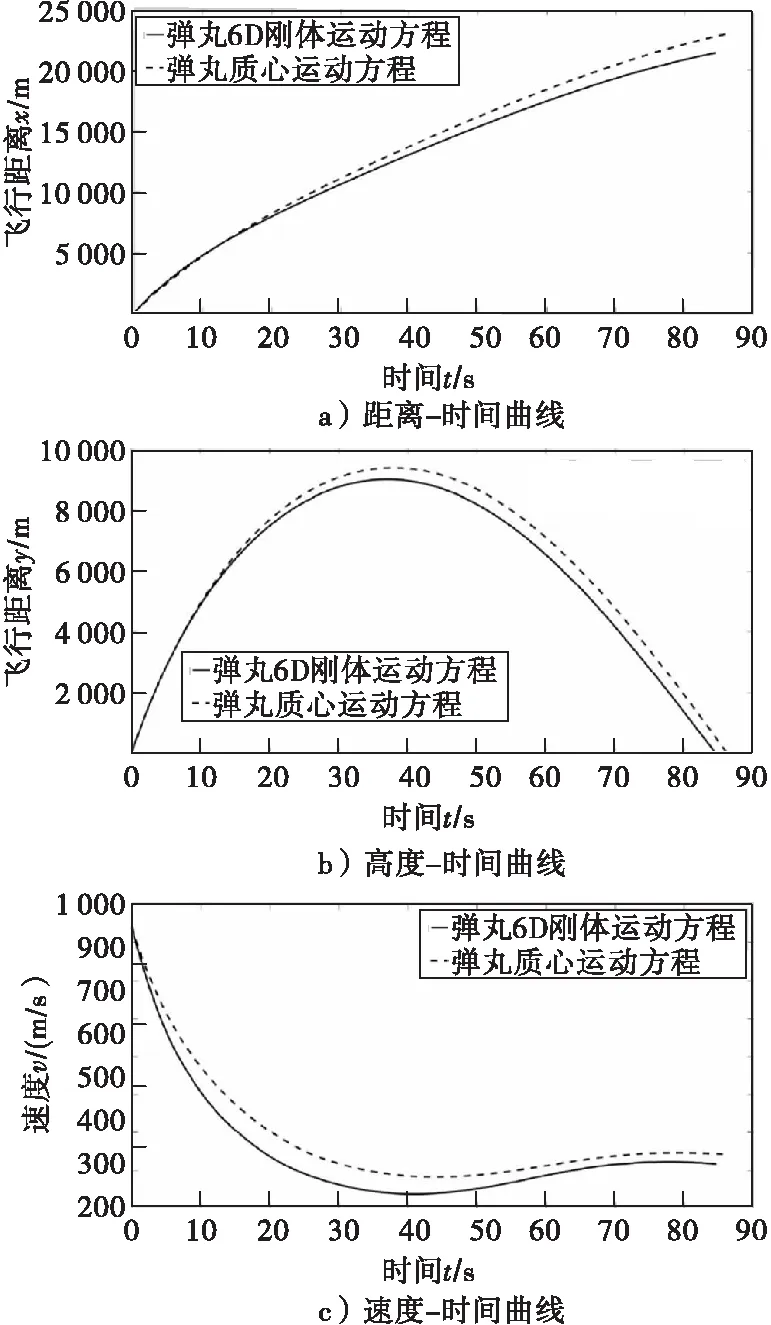
图5 6D外弹道方程与质点外弹道方程计算结果对比[73]Fig.5 Comparison of calculation results between 6D exterior ballistic equation and mass point exterior ballistic equation[73]

2.2 刚体外弹道学在引信技术领域的应用

刚体外弹道学模型能解决因弹丸绕质心运动所产生的的引信零件受力分析所需的弹道力学环境问题[3]。

2.2.1动不平衡弹丸6D刚体运动方程

由于弹丸设计、制造等原因，弹丸会存在质量分布不对称和几何外形不对称的情况。前者使弹丸质心偏离其几何中心，使弹丸惯性主轴(弹丸的旋转轴)偏离其几何对称轴(引信轴线)，后者使空气动力轴偏离几何对称轴[78]。弹丸的不对称性使得在计算弹丸外弹道6D刚体运动方程时，要去掉弹丸是完全对称体的假设条件。

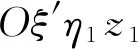
(1)

2.2.2弹丸质量偏心对章动角变化规律的影响

弹丸章动会显著影响章动力和爬行力。文献[80]总结了155 mm口径榴弹的最大章动角和偏心距以及早期、近期文献所披露的爬行力、章进力及总轴向惯性力最大值，发现章动角在9°以内时，考虑章动影响的爬行力是未考虑章动影响时的1.45倍。

弹丸质量偏心是造成章动的关键因素之一，也是影响弹丸轴向惯性力的关键因素之一，在章动角相同的条件下，每1 mm的质量偏心会增加15%～30%的轴向惯性力[80]。在有偏心同时又有初始扰动的情况下，章动现象是绕着某一章动轴线产生进动，但进动过程同时又是绕着速度方向轴线进行进动的复合章动运动，这会导致章动角发散[81]。文献[81]中以120 mm口径旋转稳定弹为例，在初速516 m/s、射角15°、初始扰动为3°条件下，通过Adams仿真对比了弹丸在无偏心和有1.6 mm径向偏心时弹丸的章动角变化规律，如图6所示。

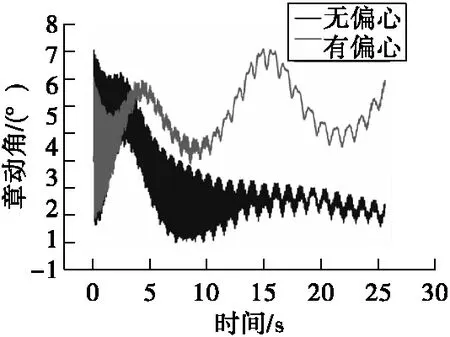
图6 120 mm口径旋转稳定弹无偏心和有1.6 mm径向偏心时章动角与时间关系[81]Fig.6 The relationship between nutation angle and time when 120 mm caliber rotary stabilized projectile has no eccentricity and 1.6 mm radial eccentricity

由图6可看出，在无偏心的条件下，在炮口处弹丸的章动角最大，随后逐渐衰减，随着弹丸初始扰动角的增大，弹丸最大章动角也随之增大。在有偏心的条件下，随着弹丸初始扰动角的增大，弹丸最大章动角仍随之增大，但章动角将无法收敛，且最大章动角比无偏心条件下的要大。

2.2.3自转规律与以往公式结果对比

以往研究弹丸转速衰减规律常采用经验公式。按复杂程度划分，比较简易的有柔格里公式、幂函数式和指数函数式[82]，它们是考虑弹带刻槽和弹体表面摩擦阻力得到的经验公式。其中柔格里公式的参数有炮口转速、弹径、弹长和极转动惯量四个，幂函数式中的参数有炮口转速和弹径两个，指数函数式的参数只有炮口转速一个。幂函数式和指数函数式这两个半经验公式形式简单，能满足弹丸和引信工程设计要求，并能用于弹丸和引信的性能估算，但未考虑极转动惯量的影响，对极转动惯量差异较大的另类弹丸(如破甲弹)，误差大于柔格里公式[83]。

比较复杂的经验公式有斯列斯金公式[84]和在此基础上改进的转速衰减模型[85]，它们考虑了弹形、弹体表面摩擦阻力、空气密度、弹道高度和空气粘度的影响。其中斯列斯金公式将弹丸分为圆柱部和圆锥部两个部分，并忽略弹带刻槽的影响，导致其计算出的转速下降缓慢，但趋势上与实测规律基本接近。对此，曾通过修正斯列斯金公式系数“0.002 44”的方式进行改进。文献[86]以59式100高榴弹在内的五种弹丸在不同发射条件下的系数值作为样本，取它们的平均系数值作为修正后的斯列斯金公式系数，修正后系数变为0.005 24，是之前的2.3倍，修正后的斯列斯金公式计算出的转速-时间曲线与实测的转速-时间曲线在趋势上和下降速度上接近。转速衰减模型则考虑了弹丸弹带刻槽的影响，文献[87]将该模型与其他经验公式的计算结果进行对比分析，从结果上看，转速衰减模型的计算误差明显小于幂函数式、指数函数式、柔格里公式和斯列斯金公式的计算误差，与修正后的斯列斯金公式计算误差接近。因此弹带刻槽对弹丸自转规律的影响不能忽略。

相比之下，6D弹道模型虽然可以计算弹丸的转速衰减规律，但是未考虑弹带刻槽和弹形的影响，仅考虑了弹体表面的摩擦阻力，理论上误差会很大。对该问题，目前还未有较好的解决方案。

而尾翼弹还受尾翼导转力矩的影响，出炮口后会促使弹丸转速迅速增加，之后受极阻尼力矩和尾翼导转力矩共同影响，转速会稳定到一个固定的值[88]，这个过程不再适合用以往的经验公式计算，但是可通过6D弹道模型仿真得到。文献[89]建立了一个基于6D弹道模型的弹丸单自由度滚转仿真模型，得到了弹丸平衡转速与速度的关系，以及平衡转速与尾翼斜切角的关系，与实测结果相比，6D弹道模型计算出来的转速值误差在5%以内。

2.2.4章动角规律

弹丸在外弹道飞行过程中飞行稳定性受章动角影响，章动角过大会导致弹丸飞行失稳，同时也可能导致引信零部件章动力过大，引发弹道炸[90-91]。章动角对弹丸飞行稳定性影响可参考文献[78]。该文献认为，保证弹丸整个外弹道飞行稳定性的关键之一就是将弹丸章动角控制在一定范围内，因此有必要知道全弹道的章动角规律。

为获取章动角数据，很多测试章动角的方法被相继提出，包括纸靶法、狭缝相机摄影法、单线阵立靶法、雷达法、光学法以及传感器法[92]，但这些方法或多或少都有一定的限制。纸靶法最早被提出，但是纸靶法测量精度较低，局限于低伸弹道的测试，并且受炮口火焰与冲击波影响，不能测量炮口处的起始章动角[93]。狭缝相机摄影法只适用于短距离弹丸章动测试。现阶段常采用弹道跟踪技术与高速摄影结合测量章动角。单线阵立靶法的测试设备操作不便，使用成本较高，且易受到天气影响[94]。雷达法对于被测弹丸外形具有较高的要求，更改了弹丸原有外形后，其空气动力学特性便很难保持一致。光学法的前期准备工作较为复杂，易受试验场地气象条件影响，试验成本较高[95]。传感器法是目前的主流测试方法，通过不同的传感器(加速度计、陀螺仪、磁传感器、红外传感器)可获知弹丸姿态变化过程中各种参量的变化[96]，这其中就包括章动角。另外，若要用传感器法测量全弹道上的章动角变化规律，需要建立相应的补偿模型，例如用地磁传感器测量全弹道上章动角变化规律时，需要建立全弹道上的磁场补偿模型[97]。

目前常采用仿真的方式获取全弹道的弹丸章动角。已有的仿真方式有Adams动力学仿真[81, 91]和LS-DYNA显示动力学仿真[98]。这两种方法都可以得到弹丸外弹道章动情况，前者需要先将弹丸模型导入Gambit和Fluent中获取气动力和力矩数据，后者则通过建立庞大的空气域模拟弹丸全弹道飞行环境。

3 总结与展望

本文针对无控弹丸刚体外弹道学模型原理和应用进行总结，得到以下结论：

1) 6D弹道模型在求解精度上高于质点外弹道学模型，但在计算速度上远不及后者，4D弹道模型与质点外弹道学模型在计算速度上接近，在解算精度上4D弹道模型更高，5D弹道模型比质点外弹道学模型的计算速度慢10倍左右，但5D弹道模型的解算精度更高。

2) 在射角小于65°时，准刚体外弹道学模型计算结果与6D弹道模型相近，在射角大于65°时，准刚体外弹道学模型在射程和偏流上与6D弹道模型差异较大。在相同初始条件下，刚体外弹道学模型计算时间远大于准刚体外弹道学模型计算时间，大约是5D弹道模型的100倍，是4D弹道模型的500倍。

3) 6D弹道模型与准刚体外弹道学模型的解算初始条件都包含弹丸模型参量、发射环境和初始扰动，它们的差异体目前气动力参量的选取不同，5D弹道模型和6D弹道模型考虑了全部的气动力参数，4D弹道模型只考虑了阻力系数、升力系数、马格努斯力系数和极阻尼力矩系数，而未考虑赤道阻尼力矩系数、马格努斯力矩系数和静力矩系数。

4) 4阶龙格-库塔法适用于无控弹丸的刚体外弹道方程计算，但不适用于有控弹丸(尤其是导弹)，当外弹道方程未知数和方程个数过多时，单纯用龙格-库塔法解算会出现发散和失真，此时应当采用吉尔法或龙格-库塔法转阿当姆斯法。

5) 刚体外弹道学模型已应用于现代武器的射表编制中，其中4D计算速度和计算精度能够满足战场需求，4D弹道模型在国内外已作为射表编制的标准模型。5D弹道模型在理论上具备编制射表的条件，具体效果还需要实际检验。6D弹道模型解算速度无法控制在5 s内，不宜作为火控弹道模型，近些年也没有用6D弹道模型编制射表的试验。就研究意义而言，在目前计算机硬件条件下，4D弹道模型的研究意义不大，5D弹道模型形式简单，有助于分析弹丸自转规律，6D弹道模型最接近实际弹丸飞行状态，有助于分析弹丸章动。

6) 刚体外弹道学模型的解算结果中包含引信零件外弹道受力环境，能够为引信惯性发火机构和解除保险机构的结构设计提供数据参考。刚体外弹道模型能够分析极端条件下(弹丸动不平衡、引信质量偏心、引信安装偏差等)引信零件的受力情况，有助于分析引信弹道炸问题。

7) 通过刚体外弹道学模型可以解算出全弹道上弹丸的转速变化规律和章动角变化规律，为弹丸和引信的抗章动、抗过载性能估算、分析和论证提供数据支持。