基于Simulink的二维弹道修正组件控制电路仿真方法
徐国泰,张晓玲,范清田,孙 振,苟 斌
(1.西安机电信息技术研究所,陕西 西安 710065;2.西北工业集团有限公司,陕西 西安 710043)
0 引言
目前,国内多家科研院所正在积极开展二维弹道修正组件的研究工作。二维弹道修正组件一般采用鸭舵修正技术方案,对常规弹药进行智能化改装,提高其打击目标的精度,降低作战效费比[1]。二维弹道修正组件的修正执行部件是磁力矩电机,二维弹道修正组件控制电路通过改变脉宽调制信号(PWM)的占空比来控制磁力矩电机产生相应的控制力矩,控制翼面固定在某一确定方向,为弹丸提供持续的修正力。
磁力矩电机是一种三相永磁同步发电机,具有结构简单、功率密度大、体积小、效率高等优点[2]。目前磁力矩电机的控制方法主要有永磁电机电枢回路串接电阻调速、斩波调压调速两种,实验证明斩波调压调速的方法为最优的控制方法[3-8]。文献[9]利用Simulink建立了永磁风力发电控制系统模型,并进行了仿真研究。文献[10]利用Simulink建立了高速永磁同步发电机PWM整流器仿真模型,通过仿真对控制原理进行了验证。
二维弹道修正组件控制电路是一种升压(BOOST)斩波控制电路,该电路系统是一个强耦合、具有非线性时变性的复杂系统[11。目前二维弹道修正组件控制电路的优化设计中需要通过大量实验对电路参数进行优化,因此提出了一种基于Simulink的二维弹道修正组件控制电路仿真方法,建立了二维弹道修正控制电路仿真模型,对电路参数进行优化设计。
1 二维弹道修正组件控制电路
磁力矩电机是二维弹道修正组件的修正执行部件,如图1所示,其转子与翼面部分固连,通过控制磁力矩电机转子的位置,即可使二维弹道修正组件翼面固定在某一确定方向。二维弹道修正组件控制电路通过控制磁力矩电机定子三相电流,调节磁力矩电机的控制力矩,克服翼面部分导转力矩,从而实现磁力矩电机转子位置控制,即翼面位置控制。
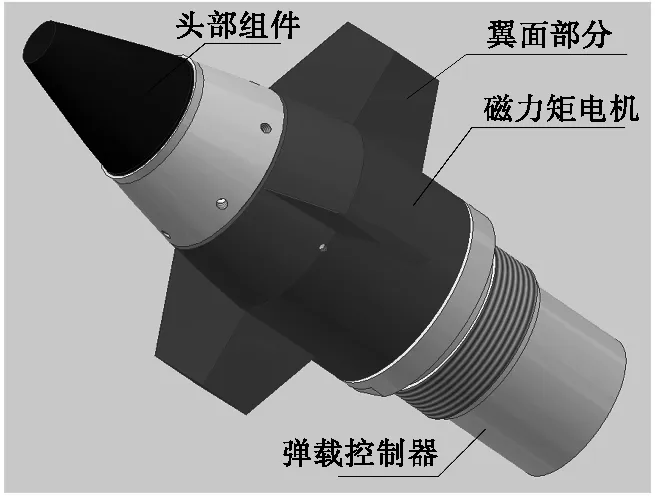
图1 二维弹道修正组件Fig.1 Two-dimensional trajectory correction kit
1.1 二维弹道修正组件控制电路模式选择
二维弹道修正组件控制电路可以采用以下两种模式:1)PWM整流模式;2)不控整流+BOOST模式。PWM整流模式如图2所示,磁力矩电机与PWM整流器相连,通过构造磁力矩电机的数学模型,得到两相旋转坐标系下d、q轴电流,调节d、q轴电流,即可控制磁力矩电机的三相电流,从而调节磁力矩电机的控制力矩[9]。采用该模式的二维弹道修正组件控制电路运行效率高,但该模式需使用6个大功率 IGBT ,控制时需输出6路PWM信号,系统控制比较复杂,系统成本也比较高。
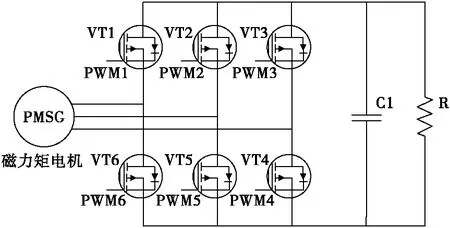
图2 PWM整流模式Fig.2 The PWM rectification mode
不控整流+BOOST模式如图3所示,磁力矩电机与二极管组成的三相不控整流桥相连,并在整流桥输出端并联滤波电容,然后加入大功率MOSFET组成升压(BOOST)斩波电路,实现控制磁力矩电机三相电流的目的,从而调节磁力矩电机的控制力矩。采用该模式的二维弹道修正组件控制电路工作稳定,仅需使用一个大功率MOSFET,控制时仅输出1路PWM信号,系统控制比较简单,系统成本大幅降低,因此二维弹道修正组件控制电路选用不控整流+BOOST模式。
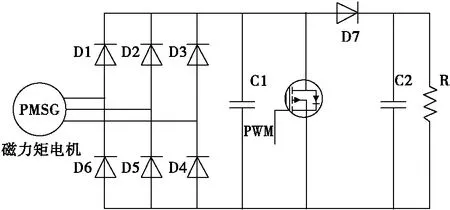
图3 不控整流+BOOST模式Fig.3 Uncontrolled rectification+BOOST mode
1.2 不控整流+BOOST工作原理
磁力矩电机属于三相永磁同步发电机,其每一相可以等效为交流电压源、相电感以及相电阻串联电路,因此二维弹道修正组件控制电路可以等效成如图4所示的电路模型,其中ea、eb、ec分别为三相交流电压源,La、Lb、Lc为三相电感,Ra、Rb、Rc为三相电阻。
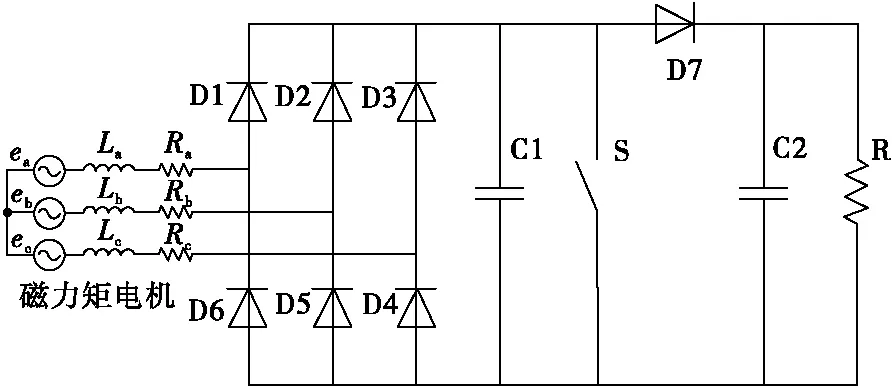
图4 二维弹道修正组件控制电路等效模型Fig.4 The equivalent model ofcontrol circuit for two-dimensional trajectory correction kit
二极管组成的不控整流桥可以将磁力矩电机输出的三相交流电转换为直流电。为了方便对二维弹道修正组件控制电路进行分析,可以将磁力矩电机+不控整流桥简化为直流电压源E串等效电感L(由于相电阻阻值远小于负载阻值,忽略不计),如图5所示。简化后的电路模型即为BOOST斩波电路,输入电流是连续的,上电开通时,会有一个幅值几倍于稳态输入电流的冲击电流流过MOSFET,因此选择的MOSFET要承受启动时的电流反应。
BOOST斩波电路工作原理是通过开关S的通断,将输入直流电压源E转换为更高的输出电压,为负载供电。当开关S开通时,二极管反向偏置,电感L中电流增大,进行储能;此阶段负载由电容C2供电。当开关S关断时,由于电感L中电流不能突变,电感上的电压极性反向保持电流为常值,电流依次流过电感L、电容C1、二极管D7、电容C2、负载R;电感释放其储能,电流开始减小,并通过二极管为电容C2充电至一个高于直流电压源的电压值。
开关S通断过程中,电感L上的电流变化趋势即为磁力矩电机三相电流的变化趋势,使得磁力矩电机输出控制力矩。通过改变PWM的占空比,即可改变开关S的通断时间,调节磁力矩电机三相电流,从而调节磁力矩电机输出控制力矩的大小。
1.3 二维弹道修正组件控制电路优化设计
二维弹道修正组件控制电路是一种具有强耦合、非线性时变性的复杂系统,因此在分析其工作原理的过程中,通过对电路系统进行简化,实现了对控制电路的定性分析。二维弹道修正组件控制电路在优化设计时,由于无法对各项参数进行定量分析,目前主要采用试验试凑的方法对控制电路参数进行优化。采用试验优化法对二维弹道修正组件控制电路进行优化,需要试验次数多,时间周期长,占用大量人力物力,因此需要对二维弹道修正组件控制电路优化方法进行改进,减少优化时间周期。
2 二维弹道修正组件控制电路仿真方法
商业软件Simulink是非常优秀的仿真分析平台,可以利用它提供的模型库搭建二维弹道修正组件控制电路仿真模型,对多工况下的控制电路参数进行仿真,实际是进行了大量的模拟实验,减少优化周期。
2.1 仿真模型建立
二维弹道修正组件控制电路有两种工作状态:无控状态和有控状态。无控状态是指二维弹道修正组件控制电路不输出PWM信号,MOSFET处于常开状态;有控状态是指二维弹道修正组件控制电路输出PWM信号,电路处于BOOST斩波控制状态。
磁力矩电机采用Simulink自带的永磁同步电机模型,利用Simulink搭建二维弹道修正组件控制电路仿真模型如图6所示,图中Pulse模块可以产生PWM信号,通过设置其参数可以改变二维弹道修正组件控制电路的工作状态。二维弹道修正组件控制电路仿真模型中磁力矩电机各项参数以及电路参数按照表1进行设置。
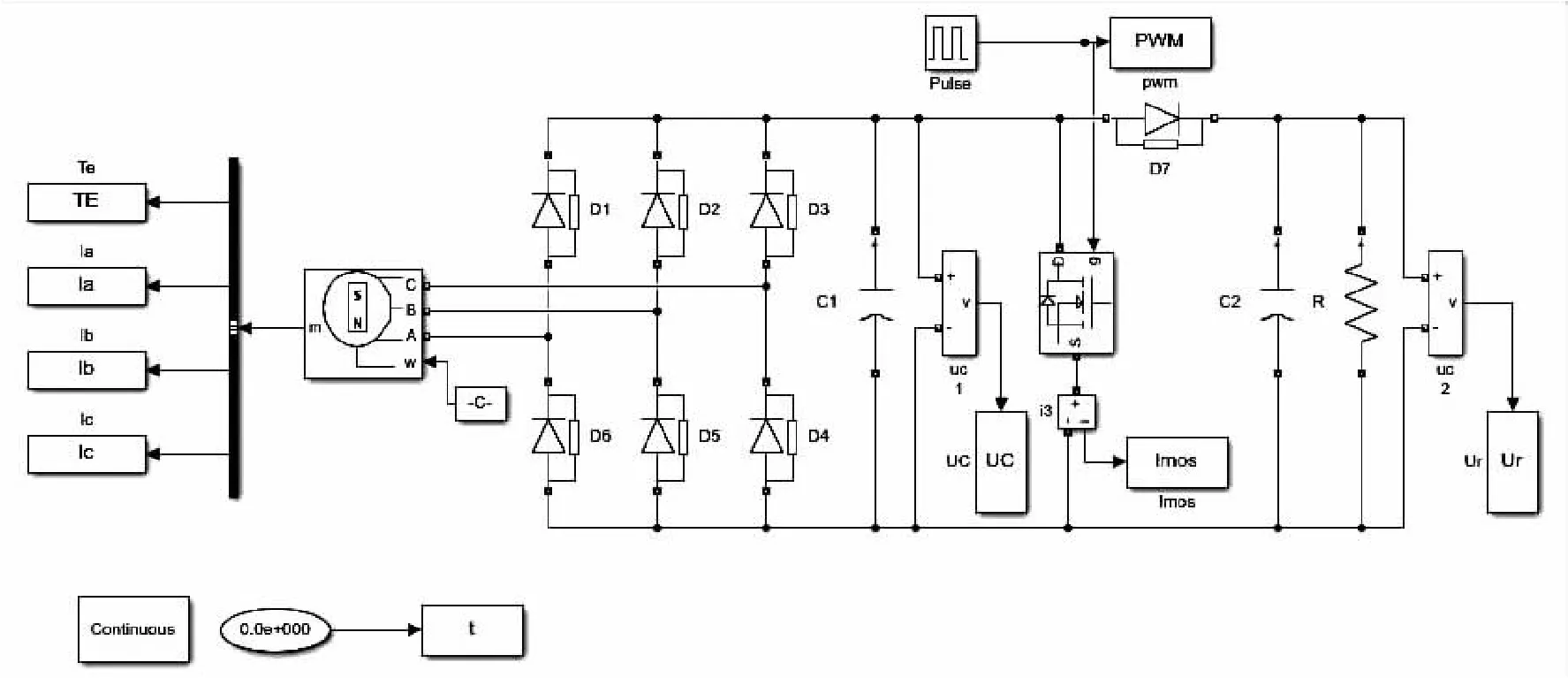
图6 二维弹道修正组件控制电路仿真模型Fig.6 The simulation model ofcontrol circuit for two-dimensional trajectory correction kit
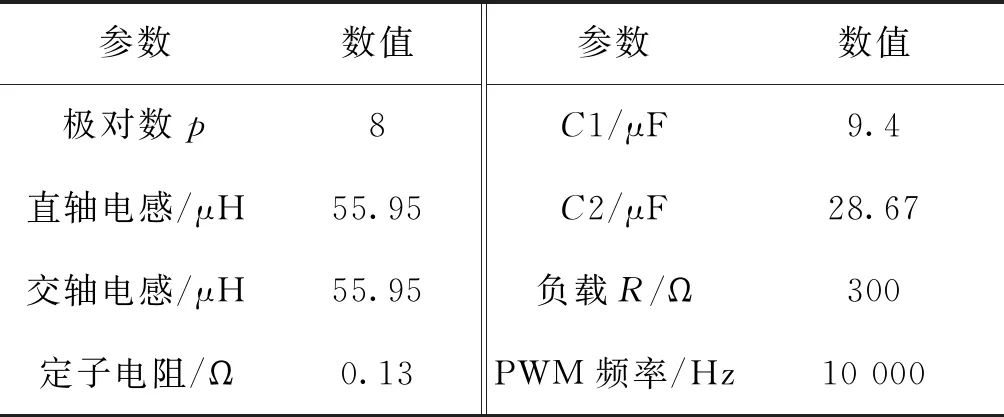
表1 二维弹道修正组件控制电路参数
2.2 仿真模型验证
为了验证仿真模型的准确性,设置PWM占空比为0,使二维弹道修正组件控制电路工作于无控状态,进行仿真。
二维弹道修正组件控制电路工作于无控状态,磁力矩电机转子转速为140~240 r/s条件下,分别进行了仿真和实验,负载R电压情况如表2和图7所示。从表2中可以看出负载电压仿真值与测试值之间最大误差为2.536%。从图7中可以看出,负载电压仿真结果线性度较好,与磁力矩电机的特性相符;实验值线性度稍差,这是由于测试误差造成的。综上所述,证明仿真模型的仿真结果与实际情况比较接近,可以用于二维弹道修正组件控制电路的仿真分析。
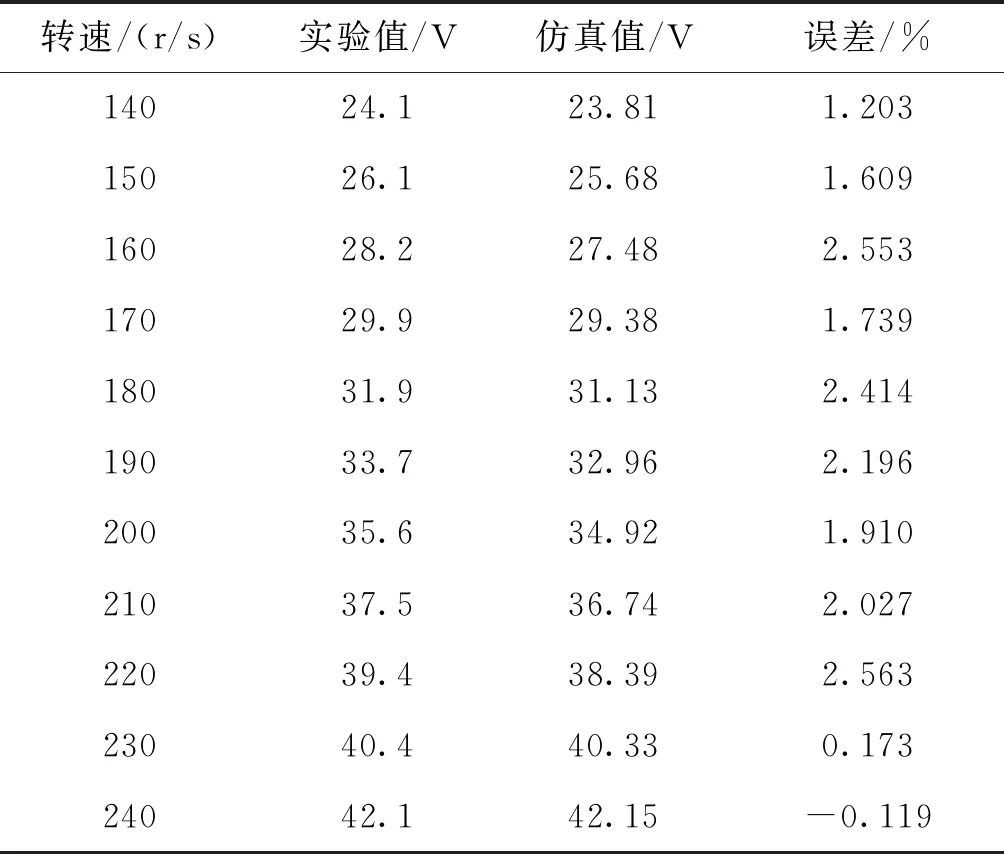
表2 无控状态下,负载电压
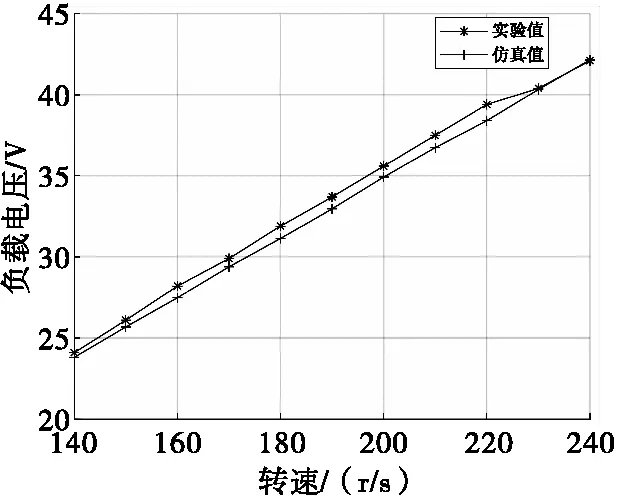
图7 负载电压Fig.7 The load voltage
3 仿真分析
二维弹道修正组件可配装于122 mm、155 mm榴弹,二维弹道修正组件工作于有控状态时,磁力矩电机转速(翼面部分相对弹丸的转速)范围为140~240 r/s,选取磁力矩电机工作于200 r/s时,分别改变负载阻值、电容容值以及PWM占空比等参数,对二维弹道修正组件控制电路进行仿真分析。
当磁力矩电机工作于200 r/s,PWM占空比为50%,对二维弹道修正组件控制电路进行仿真,控制电路参数按照表1进行设置。仿真模型中设置仿真时间为0.5 s,PWM频率为10 kHz。仿真时0~0.25 s不输出PWM信号,控制电路工作于无控状态;0.25~0.5 s输出PWM信号,控制电路工作于有控状态。
磁力矩电机工作于200 r/s,控制电路工作于有控状态时,MOSFET的电流情况如图8所示。从图中可以看出,当MOSFET处于导通瞬时,有一个高达几百安培的电流流过MOSFET,这与理论分析相符合。
磁力矩电机工作于200 r/s,控制电路中负载电压如图9所示,磁力矩电机控制力矩如图10、图11所示。控制电路工作于无控状态时,负载电压平均值为34.92 V,磁力矩电机输出力矩基本为0。控制电路工作于有控状态时,负载电压最大值为74.97 V,平均值为65.54 V;磁力矩电机输出控制力矩平均值为0.452 3 N·m。有控状态下的负载电压平均值与无控状态下负载电压相比,提高了87.6%,证实二维弹道修正组件控制电路是一种升压斩波电路。
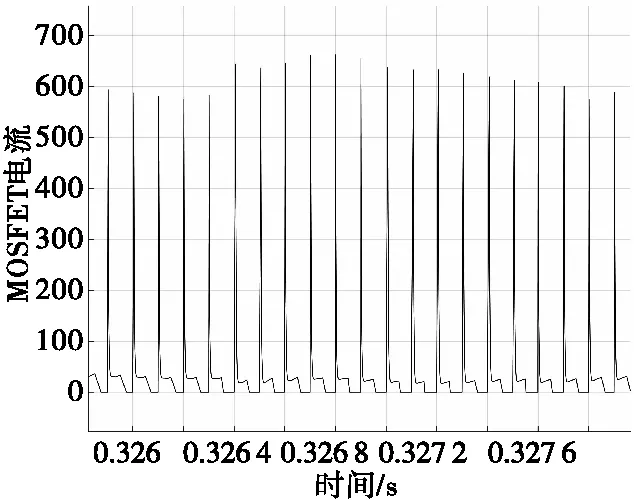
图8 有控状态下MOSFET电流Fig.8 The current of MOSFET
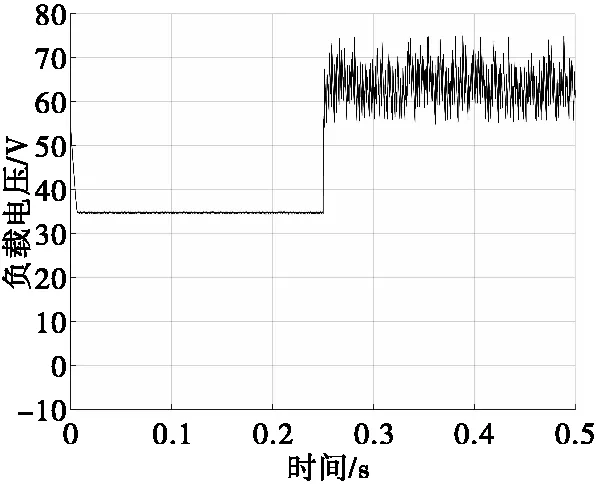
图9 磁力矩电机工作于200 r/s时的负载电压Fig.9 The load voltage of MTM working at 200 r/s
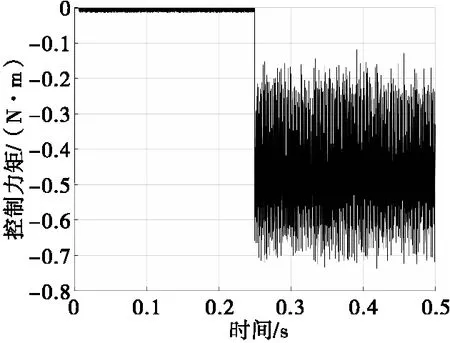
图10 磁力矩电机工作于200 r/s时的控制力矩Fig.10 The control torque of MTM working at 200 r/s
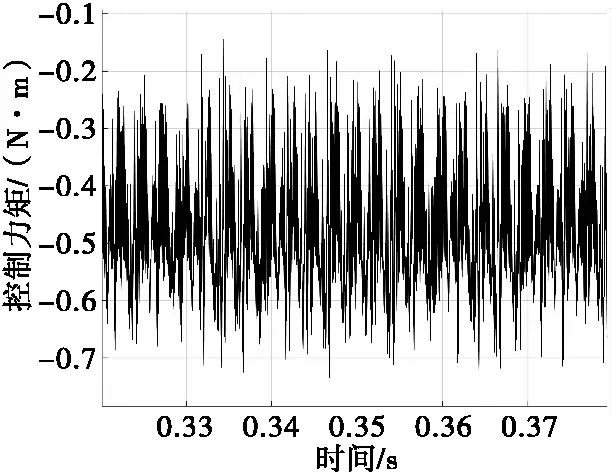
图11 有控状态下磁力矩电机工作于200 r/s时的控制力矩Fig.11 The control torque of MTM under controled working at 200 r/s
磁力矩电机工作于200 r/s,控制电路参数设置如表1,PWM占空比为50%时,分别在负载电阻阻值为10、20、50、100、300、500、1 000 Ω 的情况下对控制电路进行仿真,仿真结果如图12—图14所示。
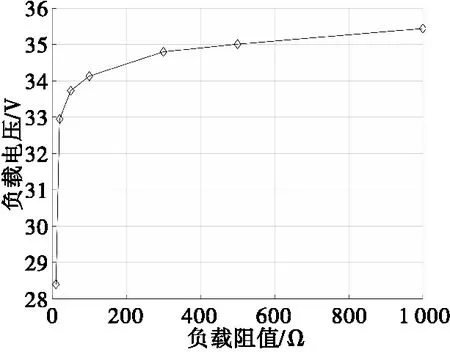
图12 无控状态下的负载电压Fig.12 The load voltage under uncontrolled
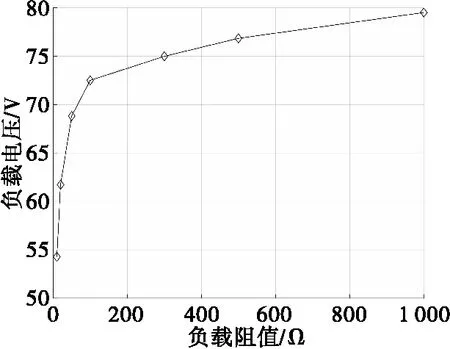
图13 有控状态下的负载电压Fig.13 The load voltage undercontrolled
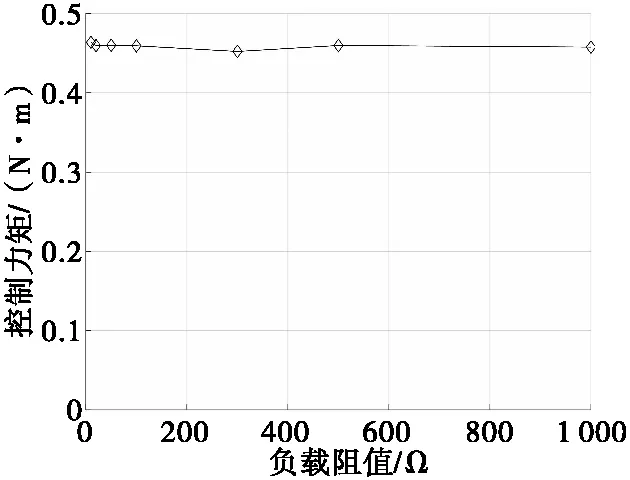
图14 有控状态下的控制力矩Fig.14 The control torque of under controlled
从图12中可以看出:无控状态下,负载阻值在10~100 Ω范围内,负载电压变化较大;负载阻值100~1 000 Ω范围内,负载电压变化不大。从图13可以看出:有控状态下,负载电压变化趋势与无控状态一致;相同负载情况下,有控时的负载电压明显高于无控时的负载电压。从图14可以看出,负载阻值的变化对磁力矩电机控制力矩基本没有影响。
在实际应用中,控制电路二极管后接DC-DC稳压电源,负载电压是DC-DC稳压电源的输入电压,需对负载电压幅值进行限制。由于负载阻值对磁力矩电机控制力矩影响不大,可以将实际电路中等效负载阻值设计得大一些,以降低有控状态下负载电压,减轻DC-DC稳压电源的选型压力。
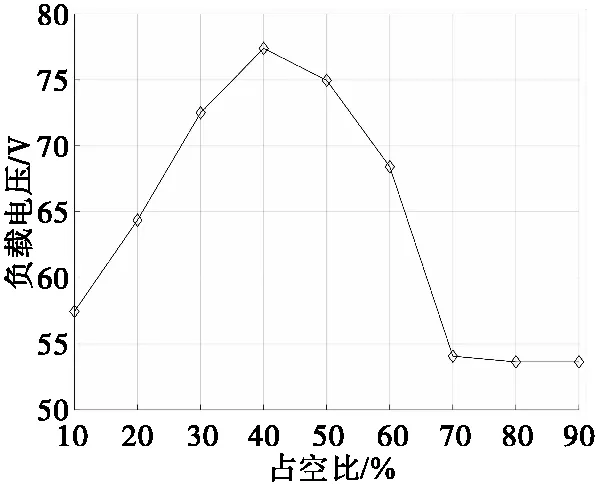
图15 不同占空比情况下的负载电压Fig.15 The load voltage under different duty cycle
磁力矩电机工作于200 r/s,控制电路参数设置如表1,分别在PWM占空比为10%、20%、30%、40%、50%、60%、70%、80%、90%的情况下对控制电路进行仿真,仿真结果如图15、图16所示。
从图15、图16可以看出:随着占空比的增大,负载电压和控制力矩都是先增大后减小;负载电压在占空比40%时达到最大值;控制力矩在占空比50%时达到最大值,仅比占空比40%时大0.003 5 N·m。在200 r/s对磁力矩电机进行控制时,可以选择占空比范围10%~40%,此时控制力矩线性度比较好,有利于控制算法的设计。
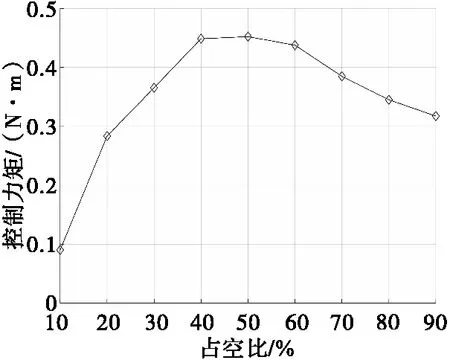
图16 不同占空比情况下的控制力矩Fig.16 The control torque under different duty cycle
磁力矩电机工作于200 r/s,控制电路参数设置如表1,PWM占空比为50%时,分别在电容容值为9.4、11.75、14.1、16.45、18.8、21.15、23.5 μF的情况下对控制电路进行仿真,仿真结果如图17—图18所示。
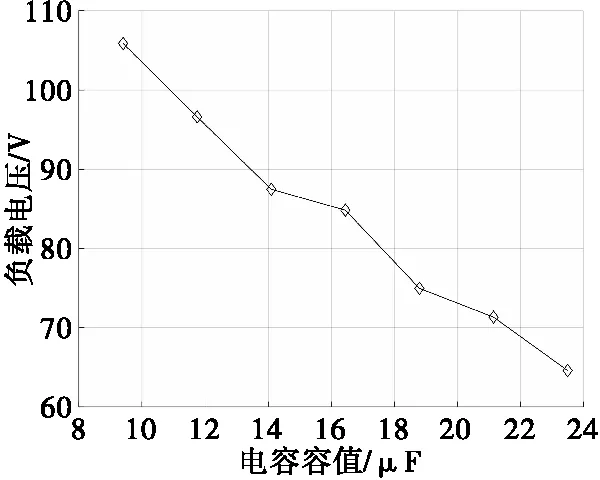
图17 电容C1不同容值下负载电压Fig.17 The load voltage under different capacitance values of capacitor C1
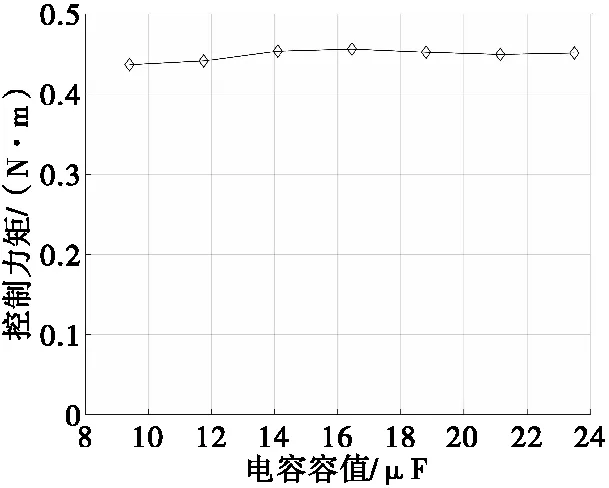
图18 电容C1不同容值下控制力矩Fig.18 The control torque under different capacitance values of capacitor C1
从图17可以看出,随着电容C1容值增大,负载电压逐渐下降;从图18可以看出,随着电容C1容值增大,磁力矩电机的控制力矩基本不变。由于磁力矩电机控制力矩不随电容C1容值变化,设计控制电路时,在体积允许的情况,应尽量选用较大的电容。
4 结论
本文提出了一种基于Simulink的二维弹道修正组件控制电路仿真方法,该方法选用Simulink中永磁同步电机作为磁力矩电机模型,并建立了控制电路仿真模型。在无控状态下,仿真模型输出负载电压与实验测试值误差范围在2.536%以内,验证了仿真模型的准确性。在有控状态下,分别改变负载电阻阻值、PWM占空比、电容C1容值,对控制电路进行了仿真,仿真结果表明:1)负载阻值对磁力矩电机控制力矩影响不大,可以将实际电路中等效负载阻值设计的大一些,以降低有控状态下负载电压;2)在200 r/s对磁力矩电机进行控制时,可以选择占空比范围10%~40%,此时控制力矩线性度比较好,有利于控制算法的设计;3)磁力矩电机控制力矩不随电容C1容值变化,设计控制电路时,在体积允许的情况,应尽量选用较大的电容。本文提出的基于Simulink的二维弹道修正组件控制电路仿真方法可以用于二维弹道修正组件控制电路的参数优化设计。

