分布熵惩罚的支持向量数据描述
胡天杰,胡文军,王士同
(1.湖州师范学院信息工程学院,浙江湖州 313000;2.江南大学人工智能与计算机学院,江苏无锡 214122)
0 引言
异常检测的目标是从正常样本中训练得到一个分类模型,进而对未知样本进行检测和识别,目前许多学者在训练样本中加入少量异常样本提升了异常检测的准确率,如带异常样本的支持向量数据描述(Support Vector Data Description,SVDD)[1]和深度神经网络(Deep Neural Network,DNN)[2]等。在实际生活的各领域中,如故障诊断[3]、网络入侵检测[4]、医疗图像诊断[5]、视频异常检测[6]和信用卡欺诈行为识别[7]等,获取正常样本较为容易,而获取异常样本需要花费很高的代价,因此异常检测方法得到了广泛使用。目前异常检测的建模方法较多,比如基于统计学习的方法[8]、基于神经网络方法[9]和基于密度估计方法[10]等。
Tax等[11]在2004年提出了SVDD方法,目标是在特征空间中找到一个能够包含所有或大多数正常样本的最小超球,作为一种典型的数据描述方法,在异常检测领域受到了广泛关注[12]。之后,很多学者对它进行了进一步的研究,并针对不同的问题提出了SVDD的改进方法,如为了增大超球体边界与异常样本之间的间隔,Wu等[13]在2009年提出了小球体大间隔(Small Sphere and Large Margin,SSLM)的支持向量数据描述方法。针对多分布数据,文献[14-15]中提出了多球支持向量数据描述(Multi-Sphere SVDD,MS-SVDD)方法。杨小明等[16]从数据的几何结构出发,综合数据全局和局部几何结构信息,在2015年提出了局部分块的支持向量数据描述(SVDD based on Local Patch,OCSVDDLP),该方法通过局部分块和局部样本重构捕捉数据的局部结构信息。此外,为了提高SVDD的决策速度,胡文军等在2011年提出了快速决策的SVDD方法(Fast Decision Approach of SVDD,FDA-SVDD)[17],该方法利用超球体球心原像将SVDD的决策复杂度降至O(1)。上述方法在建模时,都使用了相同的惩罚参数对所有松弛变量进行惩罚,即每个松弛变量的惩罚度一样,当选择不同惩罚参数时得到不同的训练模型,因此上述方法对惩罚参数过于敏感。为此,Wang等[18]在2013年提出了位置正则的支持向量数据描述(Position regularized SVDD,P-SVDD),该方法利用映射后特征空间中的样本点与均值点的欧氏距离设计不同的权重,以对相应松弛变量进行不同的惩罚。另外,Cha等[19]在数据原始空间中,基于数据分布为每个样本点设计一种密度,并将此密度作为对应松弛变量的惩罚参数,提出了密度权的支持向量数据描述(Density Weighted SVDD,DWSVDD)。
如前所述,SVDD对惩罚参数相当敏感,其本质是惩罚参数直接影响到支持向量,而支持向量又决定着超球的球心和半径。虽然P-SVDD和DW-SVDD从不同角度设计了每个松弛变量的惩罚参数,也获得了一定效果,但这两种方法都仅使用了正常样本,无法适应包含少量异常样本的场景。在包含异常样本的场景下,SVDD中训练样本的数据分布势必会变得更加复杂,一般地,在异常检测任务中,获取正常样本容易而获取异常样本困难,正常样本在数量上远远多于异常样本,且正常样本来自同一正常模式,数据分布单一,而异常样本通常来自不同的异常模式,数据分布较为复杂,因此,正常样本的分布对整体数据结构起决定性作用。为了避免少量异常样本复杂的数据分布对SVDD建模的影响,本文将从高斯核空间中正常样本的全局分布出发,提出一种距离度量,并基于此距离度量设计一种概率以评估样本正常或异常的可能性,最后利用此概率构造基于分布熵的惩罚度对样本进行惩罚,提出了一种分布熵惩罚的支持向量数据描述(Distribution Entropy Penalized SVDD,DEP-SVDD)异常检测方法。该方法针对包含少量异常样本的场景,在训练样本中加入了正常样本和少量的异常样本,并利用核空间中各个样本点到正常样本的全局分布中心之间的距离和熵的概念对各个样本点实施不同的惩罚,降低了样本在分类时的不确定度。
1 支持向量数据描述
1.1 高斯核空间
给定数据集:X={xi∈Rd|i=1,2,…,n}。其中,前m个样本是正常样本,即标签yi=1(1≤i≤m),其他样本是异常样本,即标签yj=-1(m+1≤j≤n)。一般地,数据是线性不可分的,为了解决此问题,常用方法是通过一个非线性映射函数将原始空间非线性映射至高维特征空间F,即ϕ:x→ϕ(x)。同时,利用一个核函数计算特征空间中的内积,即k(xi,xj)=ϕ(xi)Tϕ(xj),其中k(xi,xj)是某个核函数,常用核函数包括线性核、多项式核和高斯核[20]等。因高斯核能更好地捕捉数据的结构信息,故其最为常用,定义如下:



图1 高斯核空间的几何含义Fig.1 Geometric interpretation of Gaussian kernel space
1.2 传统SVDD
SVDD的目标是构造一个包含所有或大部分正常样本的最小超球,位于球面及球内的样本为正常样本,位于球外的样本为异常样本。其原始问题的数学模型为:

其中:R和a分别是超球的半径和球心,C1和C2是惩罚参数,ξ=(ξ1,ξ2,…,ξn)T是引入的松弛变量,当正常样本位于球外时,ξi>0,否则ξi=0;当异常样本位于球内时,ξj>0,否则ξj=0。利用拉格朗日技巧可得上述问题的对偶形式:

其中α=(α1,α2,…,αn)T是拉格朗日乘子。显然,式(3)是一个含等式和不等式约束的二次规划(Quadratic Programming,QP)问题。根据KKT(Karush-Kuhn-Tucker)条件可得如下结论:
结论1 对于正常样本,1)αi=0对应的样本ϕ(xi)位于超球内;2)0<αi 结论2 对于异常样本,1)αj=0对应的样本ϕ(xj)位于超球外;2)0<αj 其中,ϕ(xk)为位于超球面上任意一个样本点。对于未知样本x∈Rd,可通过如下函数进行决策: 当f(x)≤0时,x为正常样本,否则为异常样本。 图2 高斯核空间中的距离度量Fig.2 Distancemeasure in Gaussian kernel space 比较样本点与近邻样本或样本类中心之间的距离,也是异常检测的方法之一[22]。从样本分布结构来看,若样本点距离某类样本越近,则其属于该类样本的可能性越大,故距离可以评价样本点隶属的可能性。下面基于距离定义两种概率。 1)正常样本的异常概率。 2)异常样本的正常概率。 在信息论领域中,熵是样本所携带信息的度量,可对信息的不确定度进行评价[24],其定义如下: 设一个离散随机变量A={a1,a2,…,an}服从概率分布p(a),则信息熵定义为: 根据式(7)或(8)的概率pi与式(9)为各个样本点设计信息熵: 考虑到式(10)中的熵由数据的全局分布信息计算而来,因此本文将其称为分布熵。由式(10)可知,样本点属于正常或异常的概率pi越大,对应的分布熵呈现先增大后减小的趋势,这与正常样本和异常样本在分类时的不确定度趋势是一致的。 为解决SVDD中惩罚参数固定不变的问题,在目标函数中对松弛变量加权是一种有效的办法,将式(10)中每个样本点的惩罚度Wi应用至SVDD中,得到DEP-SVDD原始问题的数学模型: 需要注意的是,熵一般作为模型中独立的一项进行优化,对一个动态系统进行不确定性的度量,而本文在参数确定之后,模型系统是静态的。因此,本文借用熵的概念对松弛变量进行加权去修正SVDD的惩罚参数,如式(11)所示。 引入拉格朗日乘子构造如下拉格朗日函数: 其中,α=(α1,α2,…,αn)T≥0,β=(β1,β2,…,βn)T≥0是拉格朗日乘子。式(12)对原始变量R和ξi、ξj求偏导并置为0,对α求偏导并置为0,得: 根据α≥0,β≥0和式(15)、(16),可得0≤αi≤C1Wi,0≤αj≤C2Wj。将式(13)~(16)代入式(12)得到原始问题的对偶形式: 显然,式(17)是一个二次规划(QP)问题,根据KKT(Karush-Kuhn-Tucker)条件可得如下结论: 结论3 对于正常样本,1)αi=0对应的样本ϕ(xi)位于超球内;2)0<αi 结论4 对于异常样本,1)αj=0对应的样本ϕ(xj)位于超球外;2)0<αj 利用超球面上的任意一个样本点和球心式(14)可计算超球的半径,其表达式和式(4)相同,对于未知样本x∈Rd,可通过式(5)进行决策。 DEP-SVDD算法的实现步骤如下: 输入:数据集X={xi∈Rd|i=1,2,…,n},高斯核带宽参数σ和惩罚参数C1、C2。 输出 对于未知样本x,根据式(5)进行决策,当f(x)≤0时,x为正常样本;否则为异常样本。 步骤1 利用式(6)计算各个样本点到全局分布中心的距离di; 步骤2 利用式(7)计算正常样本属于异常样本的概率pi,或利用式(8)计算异常样本属于正常样本的概率pi;步骤3 利用式(10)计算各个样本点的惩罚度Wi;步骤4 求解式(17)的二次规划问题。 DEP-SVDD计算的时间复杂度主要包括两部分:第一部分是利用各个样本点到数据的全局分布中心的距离计算每个样本的惩罚度(步骤1~3),根据式(6)可知步骤1计算距离的时间复杂度为O(mn),得到该距离后,利用式(7)、(8)和(10)为n个样本分别计算其属于正常或异常样本的概率和惩罚度(步骤2和3),时间复杂度都为O(n)。第二部分是求解式(17)的二次规划问题(步骤4),时间复杂度为O(n3)[25]。综上,DEP-SVDD的训练过程的时间复杂度为O(n3+mn+2n),SVDD虽然少了算法步骤1~3,但仍需进行二次规划问题的求解,时间复杂度为O(n3),因此DEP-SVDD算法会略慢于SVDD。在对未知样本进行决策时,因DEP-SVDD和SVDD都使用式(5)作为决策函数,故它们的复杂度一样,均为O(n)[17]1086。 实验环境:CPU Intel Core i7-4712MQ 2.30 GHz,12 GB RAM,64位Windows 10,Matlab R2017b。 利用几种广泛使用的异常检测数据集将DEP-SVDD与SVDD、DW-SVDD、P-SVDD、K最近邻(K-Nearest Neighbor,KNN)[26]和孤立森林(isolation Forest,iForest)[27]进行分类精确度的比较,如表1所示,其中E.p和G.h分别对应Ecoli periplasm和Glass headlamps数据集,具体信息可参考http://homepage.tudelft.nl/n9d04/occ/index.htm l和http://archive.ics.uci.edu/m l/datasets.php。 表1 实验数据集描述Tab.1 Description of experimental datasets 在实验中,首先对所有样本的特征进行归一化到[-1,1]的处理,然后从正常样本中随机抽取70%的样本,从异常样本中随机抽取若干样本使得其占训练样本的20%,剩下的样本用作测试样本。所有算法都使用高斯核函数进行实验,带宽参数σ从{2n s}中选择,其中n={-6,-5,…,6},s是所有训练样本2范数均值的平方根[28];由于DW-SVDD和DEPSVDD皆利用权值对惩罚参数进行了修正,而该权值的范围在0~1,因此惩罚参数设置的范围应大于1,故将从{0.3,0.5,0.7,0.9,1.1,1.3,1.5,1.7,1.9}中选择惩罚参数,由于传统SVDD中的惩罚参数必须小于等于1,因此对于SVDD,该网格1.1及之后的值都置为1;另外,DW-SVDD和KNN需要寻找数据的K最近邻,参数K从{3,5,7,9}中选择;孤立森林方法中,孤立树的数量设置为100,子采样大小设置为256[27]418。 首先分别验证惩罚参数C1和C2对DEP-SVDD算法的影响,设置惩罚参数为1.3,高斯核带宽参数σ为2-2s,结果如图3和图4所示。 图3 惩罚参数C1对算法的影响Fig.3 Influenceof penalty parameter C1 on algorithm 图4 惩罚参数C2对算法的影响Fig.4 Influenceof penalty parameter C2 on algorithm 从图3可以看出:惩罚参数C1的取值小于等于0.7时,DEP-SVDD算法对C1较为敏感,大部分数据集的分类精度波动都较为明显,其中,在Biomed healthy数据集上达到了30%;在C1的取值大于0.7时,DEP-SVDD的分类精度趋于平稳,除Glass headlamps数据集外,对其他数据集的分类精度波动都在6%以内。从图4可以看出,除Biomed healthy数据集外,其余数据集的分类精度较为平稳,DEP-SVDD算法对惩罚参数C2的取值相对不敏感。 然后对所有数据集进行10次独立重复的实验并取均值和标准差进行比较,结果如表2所示。表2显示了DEP-SVDD与传统SVDD、解决惩罚参数敏感问题的DW-SVDD和PSVDD以及基于近邻的KNN和基于集成学习的孤立森林异常检测方法的几何精度对比。一方面,从表2中的几何精度可以看出,本文提出的DEP-SVDD对上述数据集的分类精度大多都达到了83%以上。其中,在Iris setosa数据集中KNN的分类精度最高,达到了100%;在Biomed healthy和E.p数据集中iForest方法的分类精度最高且明显高于其他方法,分别达到了98.03%和95.55%;在其余数据集中DEP-SVDD算法都取得了最好的效果。除此之外,DEP-SVDD在绝大多数数据集上的表现都要优于SVDD以及同样解决惩罚参数敏感问题的DW-SVDD和P-SVDD。另一方面,从表2中的标准差可以看出,iForest方法的稳定性明显高于其他方法,而除iForest之外的异常检测方法的稳定性都较为接近。综上所述,本文提出的DEP-SVDD在一定程度上提高了异常检测的准确率,这是因为DEP-SVDD利用正常样本作为数据的全局分布,并在特征空间中构建了能更准确描述样本间分布结构信息的距离度量,基于该距离度量设计了评估各个样本点属于正常或异常样本的概率,最后利用此概率构造基于分布熵的惩罚度对各个样本点实施不同的惩罚,解决了SVDD对惩罚参数过于敏感的问题。 表2 不同算法的几何精度 单位:%Tab.2 Geometric precisionsof different algorithms unit:% 针对SVDD对惩罚参数过于敏感的问题,本文提出了分布熵惩罚的支持向量数据描述方法(DEP-SVDD)。该方法将训练样本映射至高斯核诱导的特征空间,构建核空间中各个样本点到正常样本全局分布中心之间的距离度量来评估各个样本点属于正常或异常样本的概率,并利用此概率构造基于分布熵的惩罚度对各个样本点实施不同的惩罚。相较于SVDD,所提方法使用了更多的信息,并最小化样本分类时的不确定度,提升了算法的分类精确度,最后的实验结果表明提出的DEP-SVDD是一种有效的异常检测方法。但本文仅讨论了数据的全局分布,没有考虑数据的局部信息对算法的影响,并且只考虑了高斯核函数的使用,并没有研究其他核函数在参数条件合适的情况下的使用,这都将是下一步的重点研究方向。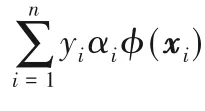


2 分布熵惩罚的SVDD
2.1 距离度量


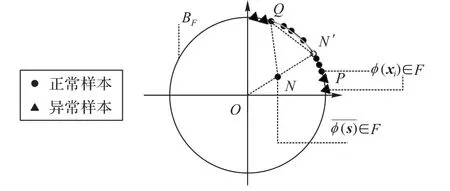



2.2 基于熵的惩罚度





2.3 DEP-SVDD

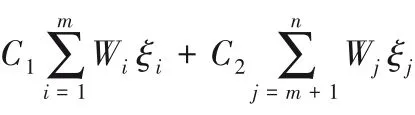


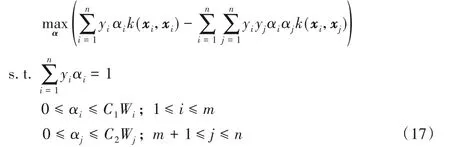
2.4 算法实现
2.5 时间复杂度分析
3 实验与分析
3.1 数据集与几何精度



3.2 实验结果及分析



4 结语

