华北落叶松林土壤物理性质空间变异与取样量
刘 帆, 郭建斌, 刘泽彬, 王彦辉, 于松平, 王 蕾, 于澎涛
(1.北京林业大学水土保持学院,100083,北京;2.中国林业科学研究院森林生态环境与保护研究所,国家林业和草原局森林生态环境重点实验室,100091,北京)
土壤水文物理性质作为土壤性质的重要指标之一[1],是土壤-植物-大气连续体的关键因子,影响着树木生长、土壤养分循环以及林地产流[2]。研究表明,受自然过程、生物(动物和植物)作用[3-4]、土壤孔隙及有机质含量等多因素的综合影响,土壤水文物理性质具有空间异质性,这种异质性的存在势必会对植物生长、物质和水文循环等过程产生重要的影响;因此,准确估算林地土壤水文物理性质将有助于深入理解这些过程的变化机制。此外,为消除空间异质性对林地土壤水文物理性质估算的影响,往往需大量的土壤样本,这必将消耗大量的人力、物力和时间成本,但目前关于林地土壤水文物理性质的最小取样量仍缺乏足够的探索,因此,有必要基于林地系统调查来科学量化土壤水文物理性质的最小取样量。
国内外关于森林土壤水文物理性质空间变异在不同空间尺度上(样地、坡面和流域等)已开展大量研究,如王政权等[5]在样地尺度上采用地统计学方法探究阔叶红松林表层土壤物理因子的空间异质性;Liu等[6]得出冠层结构和土壤持水性能是影响坡面尺度华北落叶松林土壤含水量时空变异的主要因素;王轶浩等[7]在小流域尺度上探讨土壤物理性质的空间分布特征,并建立土壤物理性质与主要影响因子的回归方程;但总体来看,有关土壤水文物理性质的研究主要集中在大尺度上,在样地等小尺度上的研究还偏少,然而实际上小尺度范围的土壤水文物理性质由于受到微地形、人为干扰和物质循环等因素的综合影响,也存在较大空间变异。此外,由于大尺度(如坡面、流域等)土壤水文物理性质数据往往是基于小尺度(如典型样地)数据经模型、遥感等技术上推得到,小尺度土壤水文物理性质的变异将会导致大尺度研究结果的偏差,因此,需格外重视小尺度森林土壤水文物理性质空间异质性的研究。
确定合理取样数量可提高土壤水文物理性质的测量精度,同时降低采样监测的成本。目前已有少量研究报道土壤性质的合理取样数量,如张广杰等[8]基于自助法确定亚热带杉木人工林和常绿阔叶林土壤养分含量的合理取样量;张志霞等[9]利用Cochran法确定黄土高原丘陵沟壑区和平原区土壤有机碳的合理取样数量,但这些研究更多是聚焦在土壤化学性质,缺乏对森林土壤水文物理性质合理取样数量的探索。
华北落叶松(Larixprincipis-rupprechtii)作为六盘山区最主要的造林树种,在当地的水源涵养、保持水土等方面发挥着重要作用,其主要分布在坡地上,存在较大的空间异质性,但对其林下土壤水文物理性质空间变异及其合理取样数量还缺乏探索,限制对华北落叶松林水土保持效益的准确评价。为深入理解华北落叶松林地土壤水文物理性质的空间变异特征,进一步为华北落叶松林土壤调查分析和取样设计以及水土保持效益评价提供科学的参考依据,笔者应用经典统计学和地统计学方法,量化华北落叶松林表层土壤含水量、土壤密度和饱和导水率的空间异质性等指标,并利用Monte Carlo模拟重抽样的方法确定土壤水文物理性质指标的合理取样数量。
1 研究区概况
研究区位于宁夏回族自治区固原市六盘山南侧的香水河小流域(E 106°12′~106°16′,N 35°27′~35°33′),面积为43.74 km2,海拔2 010~2 942 m;年均气温6.0 ℃,年均空气湿度60%~70%,年均降水量618 mm,集中在7—9月,无霜期100~130 d,属暖温带半湿润气候。土壤类型主要为山地灰褐土,石砾含量较高,母岩为石灰页岩和红色沙岩。植被类型主要以天然次生林和人工林为主,其中华北落叶松是主要的人工林树种。由于山体的作用,六盘山东南坡的雨量较大,为半湿润区,香水河小流域位于六盘山南侧,是六盘山半湿润区的代表区域;此外,华北落叶松在香水河小流域内的面积可占人工林总面积的90%,是华北落叶松的主要分布区,因而选择该小流域作为研究区。
选取典型华北落叶松人工纯林建立研究样地,面积大小为900 m2(30 m×30 m),海拔为2 410 m,坡向为东南坡向,地形相对均一,平均坡度为21°。林冠郁闭度为0.73;林下灌木稀少,覆盖度仅为5%左右,主要灌木有蒙古荚蒾(Viburnummongolicum)、秦岭小檗(Berberiscircumserrata)等;草本覆盖度在40%左右,优势种为东方草莓(Fragariaorientalis)和苔草(Carexspp.)。样地具体林分特征如表1所示。研究区华北落叶松均为同年栽植,经营历史相近[10],由于研究样地位于自然保护区内,受人为活动影响较小。样地内林木平均胸径、树高等生长特征和郁闭度、叶面积指数等林分结构均接近于研究区坡面华北落叶松的平均水平(19.9 cm、16.8 m和0.74、3.11)[11],因而研究样地具有典型性。

表1 样地林分特征
2 材料与方法
2.1 采样与测定方法
2015年7月,按照均匀布点的原则,将30 m×30 m的样方分割为100个3 m×3 m的小样方,为便于记录各取样点位置,将每个小样方的中心位置作为取样点(中心点有植被的,取样点做适当偏移),利用环刀(体积为200 cm3)取表层(0~20 cm土层)的土壤样本,共取100个样品,取样时在表层土的中部进行取样,并对每个样点的样品进行标号,并记录其空间坐标,为避免采样过程中样地土壤含水量产生较大变化,采样在临近傍晚时进行。
样品带回实验后,立即称其鲜质量,然后利用双环刀有压入渗法测定饱和导水率,测定完毕后将其放置在80 ℃的烘箱内烘干至恒质量,计算土壤含水量和土壤密度。
2.2 数据分析
应用经典统计学[12]和地统计学[13]对数据进行处理与分析,数据的描述性统计分析在SPSS 24.0软件中进行,利用地统计软件GS+9.0进行半方差函数计算及模型拟合,Kriging插值和绘图在ArcGis10.4.1中完成。利用Monte Carlo模拟抽样的方法[14],确定5%和10%误差水平下各指标的最佳取样量,方法和原理如下:首先,将100个样点的土壤含水量、土壤密度和饱和导水率实测值作为Monte Carlo随机抽样的初始值;然后,分别对100个取样点的各指标测定值进行不放回抽样(每次抽样数量2~100个),重复抽样1 000次,以获取足够的随机样本[14-15],计算上述指标测定值在不同取样数量下的平均值,这一过程可保证从固定的100个取样点中随机模拟可能出现的2~100取样点的平均值;最后,计算不同取样数量各指标的平均值和置信区间(90%和95%),绘制其变化范围。根据各变量的平均值及其置信区间随取样数量的变化,确定在5%和10%误差范围内各指标的最少取样量。该模拟在R 3.6.1软件进行。
3 结果与分析
3.1 表层土壤含水量、土壤密度及饱和导水率统计特征
由表2可知,土壤含水量变化范围16.61%~29.06%,变异系数0.23;土壤密度变化范围0.69~1.21 g/cm3,变异系数0.11;土壤饱和导水率变化范围为0.17~2.18 mm/min,变异系数0.47。总体来看,土壤含水量、土壤密度和饱和导水率均属中等变异,但土壤饱和导水率的空间变异程度较大,土壤密度的空间变异程度较小。S-W值是通过Shapiro-Wilk检验方法检验是否符合正态分布的指标,土壤含水量、土壤密度和饱和导水率的S-W值分别为0.08、0.81和0.07,均>0.05,服从正态分布。

表2 土壤含水量、土壤密度和饱和导水率的统计特征
3.2 表层土壤含水量、土壤密度及饱和导水率空间变异特征
3.2.1 土壤水文物理性质的半方差函数分析 土壤含水量、土壤密度和饱和导水率的半方差函数均符合指数模型(表3和图1);块金值均为正值;块基比分别为0.043、0.119和0.075,均具有强烈的空间自相关性;变程分别为8.07、4.38和3.12 m;表明土壤含水量的空间自相关性范围较大,其次为土壤密度,土壤饱和导水率的空间自相关性范围较小。

表3 土壤含水量、土壤密度和饱和导水率的半方差函数理论模型及其相关参数
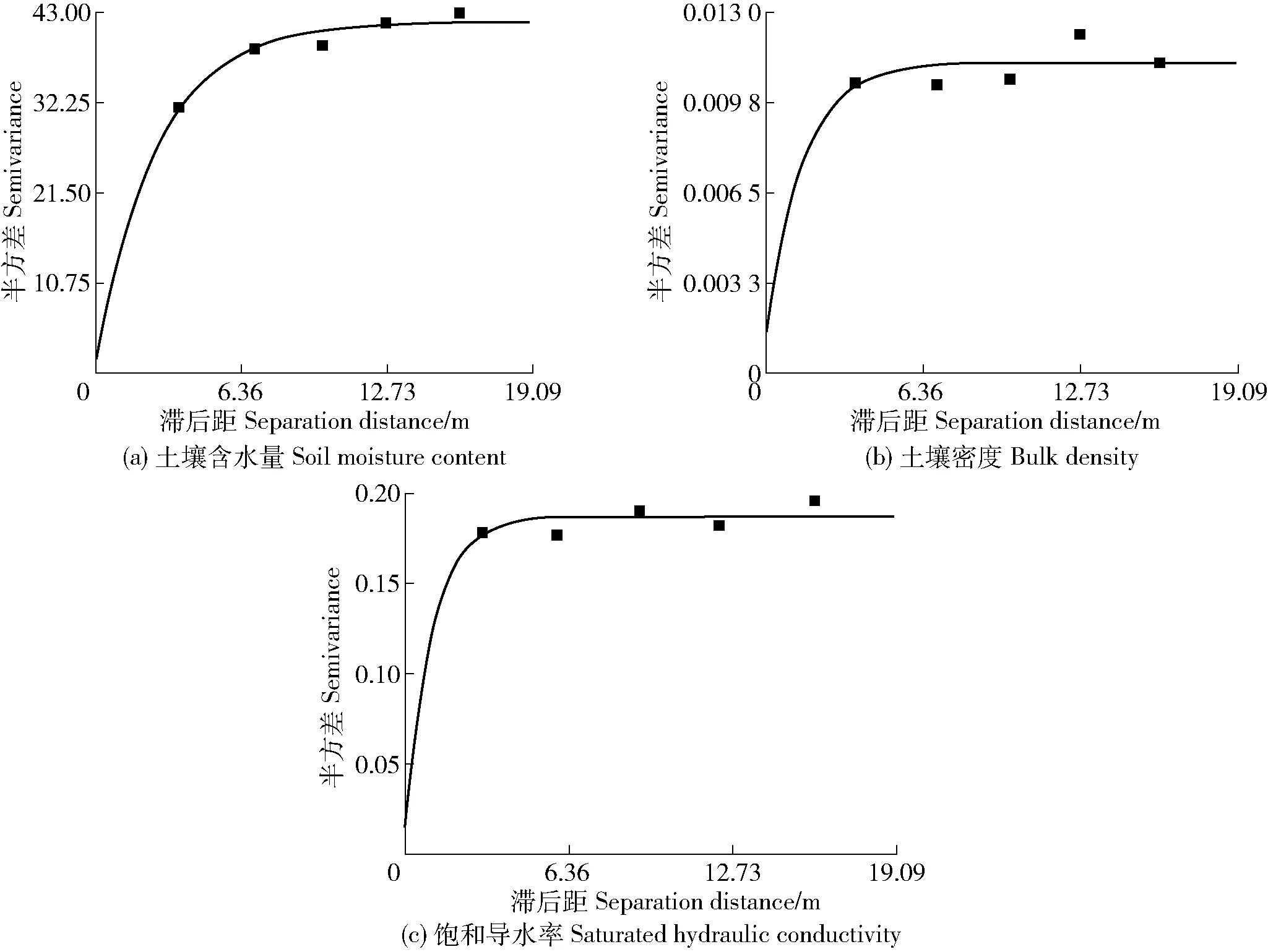
图1 土壤含水量、土壤密度和饱和导水率的半方差函数图Fig.1 Semi-variogram of soil moisture content, bulk density and saturated hydraulic conductivity
3.2.2 土壤水文物理性质的空间分布格局 应用Kriging插值法绘制样地内土壤含水量、土壤密度和饱和导水率空间分布格局图。由图2可知,土壤含水量、土壤密度和饱和导水率具有明显的空间异质性,斑块状明显,且斑块小而多,在相近区域大小差异较明显,连续性较差。土壤含水量在整个样地内无明显的变化规律;而土壤密度从总体上呈样地中心大于四周的分布格局,且样地上部的土壤密度大于下部;相较于土壤含水量和密度,土壤饱和导水率的空间异质性更强,斑块更小,空间分布格局更为复杂。
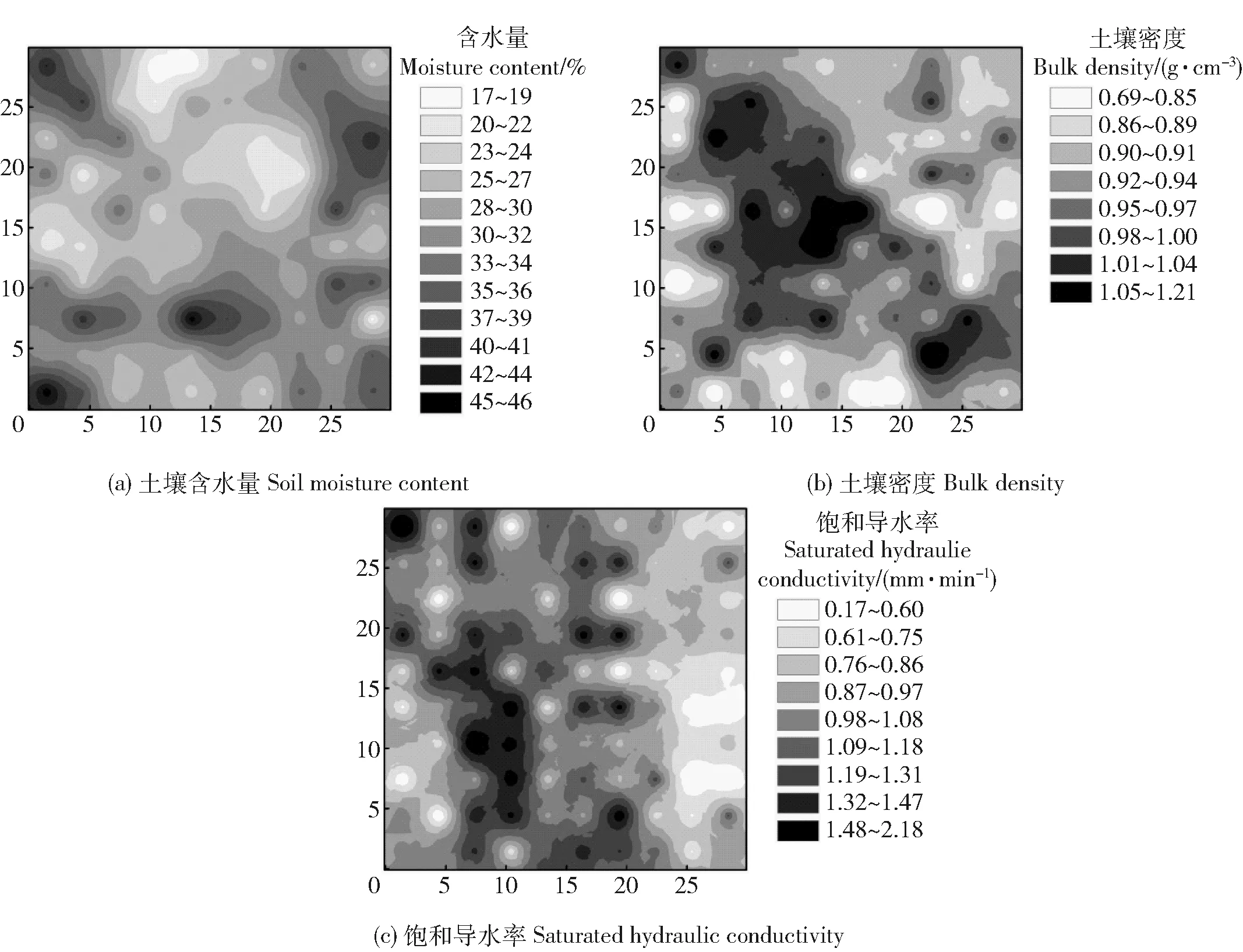
图2 土壤含水量、土壤密度和饱和导水率的空间分布图Fig.2 Spatial distribution of soil moisture content, bulk density and saturated hydraulic conductivity
3.3 合理取样数量的确定
由图3可知,随取样数量的增加,土壤含水量、土壤密度和饱和导水率的平均值和置信区间均逐渐向内收缩。土壤含水量在90%置信区间下,取样数量≥13个和≥35个时,所测土壤含水量控制在10%和5%误差水平;在95%置信区间下,取样数量≥18个和≥45个时,所测土壤含水量控制在10%和5%误差水平内。土壤密度在90%置信区间下,取样数量≥4个和≥13个时,所测土壤密度控制在10%和5%误差水平内;在95%置信区间下,取样数量≥5个和≥15个时,所测土壤密度控制在10%和5%误差水平内。土壤饱和导水率在90%置信区间下,取样数量≥34个和≥70个时,所测土壤饱和导水率控制在10%和5%误差水平内;在95%置信区间下,取样数量≥45个和≥75个时,所测土壤饱和导水率控制在10%和5%误差水平内。
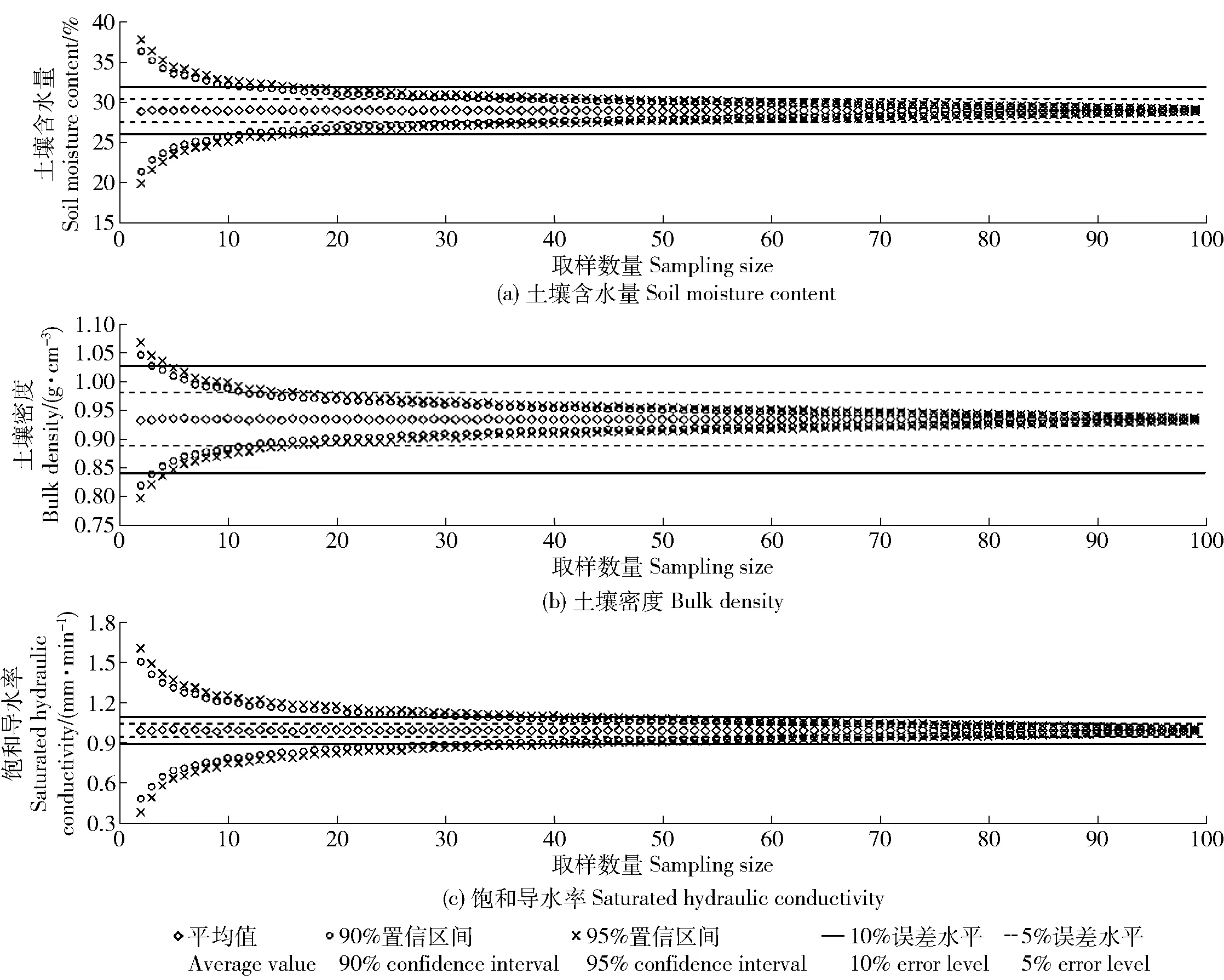
图3 Monte Carlo模拟的土壤含水量、土壤密度和饱和导水率平均值和置信区间随取样数量的变化图Fig.3 Variations of the average and confidence interval of soil moisture content, bulk density and saturated hydraulic conductivity simulated by Monte Carlo as the number of samples
4 讨论
4.1 表层土壤含水量、土壤密度和饱和导水率的经典统计特征
本研究中,表层土壤含水量变异系数为0.23,属中等变异,这与刘宇等[16]对同一研究区华北落叶松林的研究结果一致,已有研究表明,植被覆盖(如叶面积指数)、枯落物量等均会导致土壤含水量的空间变异[17],而研究区华北落叶松林冠层叶面积指数和林下枯落物量均存在较大空间变异[14,18],这可能是导致土壤含水量属中等变异的原因。土壤密度变异系数为0.11,属中等变异,这与耿韧等[19]在黄土丘陵区刺槐林地研究的土壤密度呈弱变异(变异系数0.09)的结果不尽相同,这可能是研究区域的石砾含量和土壤有机质含量具有较大的空间变异所导致的[7]。土壤饱和导水率变异系数为0.47,属中等变异,土壤饱和导水率变异程度与李平等[20]在黄土高寒区退耕林地的研究结果一致。土壤饱和导水率的大小与土壤孔隙度密切相关,本研究林地的土壤饱和导水率变异程度与黄土高寒区退耕林地的差异不大,可能与两样地内石砾含量较多,土壤孔隙度较大有关。
已有研究表明,土壤饱和导水率的变异程度高于土壤含水量和土壤密度[21-22]。本研究得到相同的结论,说明与土壤含水量和土壤密度相比,土壤饱和导水率在样地内的离散程度更大,可能是由于其受多种环境因素的影响,导致空间分布更加离散。
4.2 表层土壤含水量、土壤密度和饱和导水率的空间结构特征
本研究华北落叶松林地土壤含水量、密度和饱和导水率均具有较明显的基台值,说明三者均具有明显的空间依赖性。土壤含水量的块基比较小,表现出强烈的空间自相关性,说明在样地尺度上,实验误差不是造成土壤含水量空间分布的主要原因,其空间变异主要由微地形、土壤特征、冠层结构、林下覆被物(如草本覆盖度、枯落物生物量等)等立地环境条件所决定[23]。有研究[24]表明,土壤密度与土壤有机质含量呈显著负相关,与坡向余弦、植被类型、砾石含量、海拔呈显著正相关。笔者发现,土壤密度与石砾含量呈显著正相关(P<0.01),即石砾含量愈高,土壤密度愈大,这与张梦旭等[24]得到的土壤密度受到土壤质地影响的研究结果基本一致。土壤饱和导水率主要与土壤质地、坡度、土壤孔隙、含水量以及植被覆盖密度和土地利用类型[20]有关。笔者发现,土壤饱和导水率的块基比较大,空间自相关性较弱,说明在当前观测尺度上,土壤饱和导水率空间变异受人类活动干扰、实验误差等随机因素的影响较大[25],而上述内在因子对其变异程度的影响是有限的。
变程可反映土壤水文物理性质在空间上的变异尺度,本研究中,土壤密度和饱和导水率的变程较小,说明其空间连续性范围较小;但土壤含水量的变程较大,表明其空间连续性范围较大。研究样地土壤含水量和土壤密度的变程与王政权等[5]和耿韧等[19]研究结果相比偏小,这可能是由于研究尺度不同造成。已有研究表明,空间变异受研究尺度的影响[26],本研究样地大小比王政权等的(40 m×40 m)偏小,这或许是其土壤含水量和土壤密度变程小的原因。土壤饱和导水率的变程与Mertensa等[27]的研究结果相比偏大,可能是不同植被类型的根系结构差异影响了土壤饱和导水率的空间变异程度[21]。
4.3 合理取样量的确定
土壤水文物理性质有明显的空间异质性,为确保林地土壤水文物理性质评估的准确性,需布设大量的采样点,但若过度增加采样点将造成不必要的人力、物力和时间的浪费,所以需科学地量化在不同误差条件下(如5%或10%误差水平)的合理采样数量。目前关于林地土壤性质合理采样数量的量化仅限于土壤化学性质,如有机碳、有效磷、速效磷等[8],很少有研究量化土壤水文物理性质的合理取样量。从本研究量化的样地土壤含水率、土壤密度和饱和导水率的合理取样量来看,不同指标所需的最小取样量存在差异,土壤密度所需取样量最小,土壤饱和导水率所需取样量最大。然而,在实际的土壤取样中往往采用相同的取样标准,这将导致某些指标取样量不够,而某些指标取样量过多。因此,在进行土壤取样时需提前确定相关指标的合理取样量,这既能保证测定指标的精度,又可减少不必要的时间和经济投入。从统计分析与合理取样量的研究结果来看,研究变量的变异程度越高,其在一定样地范围内所需的取样数量越多;反之,则所需的取样数量越少,这与孙聪等[28]的研究结果一致。
由于笔者只在特定区域选取1个典型样地进行研究,所得的结果(数值)还不具有普遍的应用价值,但研究结果所揭示的合理取样数量取决于空间变异程度对于未来优化取样设计具有重要意义;本研究确定合理取样数量的方法也可供其他地区进行参考;此外,有研究表明,合理取样数量取决于指标的变异程度[29],本研究确定的华北落叶松林地土壤水文物理性质指标的合理取样数量,也可供相同和相似区域(土壤性质的变异程度类似)取样设计时参考。

