基于改进参数协进化和声搜索算法的配电网重构

邹 锐,王超学

(西安建筑科技大学信息与控制工程学院,陕西 西安 710055)

0 引言

配电网重构指满足其拓扑结构呈辐射状[1]、在电压不越限等约束下[2],通过打开或闭合开关改变网络负荷,从而实现降低网损、提升供电质量等目标[3]。 其对实现智能电网的建设具有重要意义[4]。

配电网重构是非确定性多项式难题(nondeterministic polynomial hard,NP-hard) 组合优化问题[5]。 近年来,智能优化算法,如遗传算法[6]、粒子群算法[7]、和声搜索算法(harmony search algorithm,HSA)[8]等,被广泛应用于配电网重构中。 其中,HSA是一种新颖的智能优化算法,对所有可能解向量的搜索程度高,且可调参数多,在寻优性能上更优于遗传算法等其他智能优化方法[8-9]。 HSA 由学者Geem Z W在2001 年提出[10],由学者Srinivasa 在2011 年应用于配电网重构中。 文献[9]表明HSA 的收敛性能显著优于改进的禁忌搜索算法和遗传算法,但同时也指出就配电网重构问题而言,HSA 中需要预设的2 个参数对算法寻优性能会产生重要影响。 文献[11]提出一种自适应的参数确定方法,可避免直接确定参数以提升算法的鲁棒性,但未将这种方法应用于配电网重构中。文献[12]～文献[14]分别提出了启发式策略、自适应策略及引入混沌序列策略以克服参数对算法性能的影响,但消耗在局部寻优的迭代次数显著增多,或并没有进一步说明算法的寻优性能。 文献[15]采用参数协进化策略确定HAS 中的2 个参数。 试验结果显示,参数协进化策略的HSA 在收敛性能方面具有显著优势,但同时也存在反馈环较长导致的算法计算代价较大的问题。

除了算法本身的性能优化,在配电网重构过程中,包括HSA 在内的智能优化算法寻优过程产生的解向量是以随机方式生成的,因此会出现大量不符合配电网辐射约束的不可行解,进而降低算法的收敛性能。文献[15]、文献[16]基于图论的思想,提出一种支路断开原则来控制算法中新解的生成,可以极大地降低不可行解的生成概率。 但这些启发式规定在少数情况下仍会产生不可行解。

针对上述问题,本文首先使用并改进参数协进化策略的和声搜索算法,将HSA 的参数和声库选择概率(harmony memory considering rate,HMCR)以及音调调节概率(pitch adjusting rate,PAR)作为优化目标,使用粒子群算法寻优确定;对新和声分量的微调方法进行改进,克服参数音调调节带宽(bandwidth,BW)应用于配电网重构中难以确定的问题。 同时,考虑到参数协进化策略反馈较长导致算法计算性能不佳的问题,采用辅助新和声策略对算法进行优化。 最后,提出了产生可行解的4 个必要条件,并通过建立节点编号矩阵降低不可行解的生成概率。

1 配电网重构的数学模型

配电网重构的优化目标一般是网络损耗最小、供电质量最高等。 当网络损耗最小时,供电质量、负载均衡度等也趋于最佳。 本文以网络损耗最小作为所提出方法的目标函数:

式中:Nb为配电网支路总数;Ri为支路i的电阻;Vi为支路i的末端电势;Pi为支路i的有功功率;Qi为支路i的无功功率;Ki为支路i上开关的状态,0 为断开、1 为闭合。

式(1)中的目标函数通常还包括如下约束条件。

①网络拓扑结构约束条件:

式中:g为当前网络拓扑结构;G为所有满足辐射状网络结构,并且无环网和孤岛。

②支路电压约束条件:

式中:Vimax和Vimin分别为节点i处电势的上、下限;n为网络的节点个数。

③支路容量约束条件:

式中:Sj和Sjmax分别为流过支路j的功率值和最大容许功率值。

2 改进的参数协进化和声搜索算法

2.1 和声搜索算法

和声搜索算法将目标函数视为对和声评价,将解xi,j比作各和声音调,算法的迭代过程比作指挥者寻找最美和声的过程[17]。 文献[10]中的基础和声算法流程如下。

首先,随机生成若干解xi,j,置于和声记忆库(harmony memory,HM)中。 设HM 的大小为HM。

式中:r′及后续出现以r为底的符号均为区间(0,1)内独立同分布的随机数;k∈[1,SHMS];RHMCR为HMCR 大小。

当xnew,j=xk,j时,基于PAR 进一步选择是否对新和声进行微调:

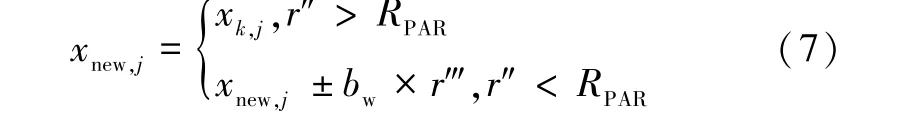
式中:bw为音调调节带宽;RPAR为PAR 大小。

进一步将目标函数minf作为适应度函数,将HM中解向量与新和声xnew的适应度进行比较,更新HM,同时根据预设最大迭代次数重复这一过程。 最终选取HM中的最优解向量,完成寻优。

2.2 改进的参数协进化和声搜索算法

基础HSA 中,式(6)、式(7)中需要预设的参数RHMCR、RPAR、bw的取值范围会影响算法在当前迭代计算中是倾向于全局搜索还是局部搜索。 此外,HSA 应用于配电网重构时,解向量各分量的具体值为网络各开关的编码,在式(7)中不具有实际的物理意义。 因此,难以通过直接定义bw来影响新和声的扰动大小。

本文使用基于粒子群参数协进化策略,将RHMCR、RPAR的确定作为优化目标,并使用粒子群优化(particle swarm optimization,PSO)算法进行寻优。 PSO算法的寻优过程如下 。

重复式(8)、式(9),到达最大迭代次数后,所得全局最优解gb即为PSO 搜索到的最优解,完成寻优。

将PSO 的种群PS 作为共生种群、HSA 的种群HM作为原始种群,则基于粒子群参数协进化的和声搜索算法的一般步骤为如下。

①确定PSO 寻优目标为某一组参数组合HP=[RHMCR,RPAR],基于式(8)、式(9)开始寻优。

②根据步骤①所得HP输入给HSA。 HSA 基于式(6)、式(7)开始寻优,并重复T次(目标为某一组开关组合使得网损最小,即minf)。

④重复步骤①至步骤③,在满足停止条件时输出最优解。

因此,基于PSO 参数协进化的和声搜索算法中,PSO 本身不能直接计算适应度函数,而是需要给HSA输入HP后通过式(6)、式(7)计算得到适应度,从而根据式(8)、式(9)更新HP。 HSA 本身也不能直接寻优,而是需要依靠PSO 输入的HP才能通过式(6)、式(7)进一步计算。 基于粒子群参数协进化的和声搜索算法原理如图1 所示。

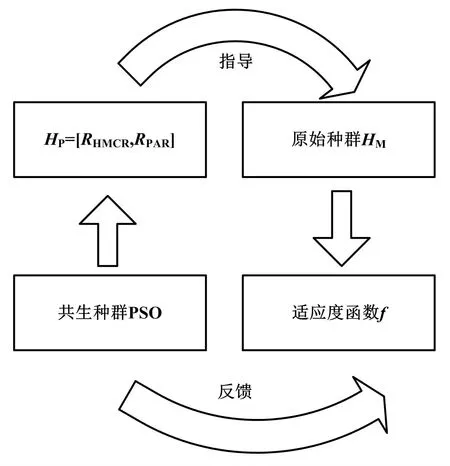
图1 基于粒子群参数协进化的和声搜索算法原理图Fig.1 Schematic diagram of harmony search algorithm with parameters co-evolution based on particle swarm optimization

虽然参数协进化策略可以自适应地确定RHMCR、RPAR和提升算法收敛性能,但为了保证算法的鲁棒性,需要在步骤②的HSA 每步迭代中,基于HP重复T次筛选最优解向量[15-18]。 当算法在第t代陷入局部寻优时,HSA 反馈PSO 重新寻找HP,PSO 在(t+1)代指导HSA 寻优,完成(t+1)代所有计算后,才能重新反馈PSO 进行HP的更新。 即使算法在1 代就可以跳出局部寻优,也需要调用PSO 进行2 次计算,调用HSA 进行2×T次计算。 算法调用次数数倍于普通优化算法。在算法局部寻优时,反馈环节较长,可能导致计算量急剧增大的问题。

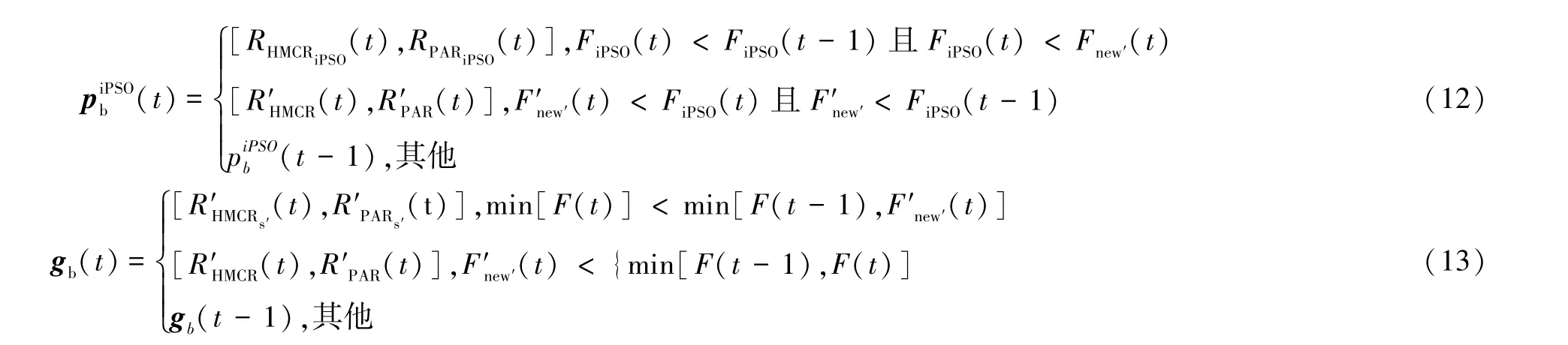
另一方面,为了避免bw难以直接确定的问题,使用并改进一种解决连续性优化问题的自适应微调方法[11]。 对配电网中的节点按环路编码后,将式(14)、式(15)随机用于和声微调步骤。

式中:a为解向量分量对应环路的索引值;nnew,j为对应环路的索引值;rd为区间[0,1]内的随机数。

当算法迭代至后期时,某些适应度较高的分量会大量保留,则式(14)、式(15)的第二项会趋于0,即不再进行微调。 这在避免直接确定bw的同时也提升了算法后期的局部搜索能力。

2.3 避免不可行解的处理方案

包括和声搜索算法在内的智能优化算法随机生成解向量的特点,可能导致大量不符合配电网辐射状约束的重构解产生。 因此,在使用所提出算法进行配电网优化重构前,基于配电网的拓扑结构,提出一种避免不可行解出现的必要条件,并通过建立节点编号矩阵产生可行解。

根据图论,配电网中与某个节点相邻的节点个数称为度。 度大于2 的点为T 型点[19]。 网络中某支路被若干重构环路所公用的支路定义为公用支路组。 基于T 型点,公用支路组的类型可以定义为2 类:T 型点内部公用支路组,即相邻2 个T 型点之间的支路组;T型点外部公用支路组,即除了内部公用支路外,与T 型点或2 个相邻T 型点相连的其他公用支路组。 以IEEE 33 节点系统为例,IEEE 33 节点配电网网络接线如图2 所示。 其中:3-4-5 为公用支路组;3、6、8、9 为T型点;6-7-8 为节点6 和节点8 的内部公用支路组;33,6-26-27-28,3-4-5 为节点6、节点8 的外部公用支路组。

图2 IEEE 33 节点配电网网络接线图Fig.2 Wiring diagram of IEEE 33 node distribution network

根据不同的T 型点和公用支路组,可以得出以下产生可行解的必要条件。

条件1:在随机产生重构时,每条环路上只能随机断开一条支路组,且每条支路组只能断开一条支路,即需保证节点的度大于1。

条件2:同1 条公用支路组只能被打开一次。

条件3:无论是1 个T 型点,还是2 个相邻T 型点,其所有的外部公用支路组都不能同时被断开。

条件4:若2 个相邻T 型点之间的内部公路组中只有2 条支路,则这2 条支路不能同时被断开。

基于上述条件,产生可行解具体步骤如下。

①建立节点编号矩阵A。 其中:行数为重构环数目N,列数为所有重构环中最大的支路数目,即除去电源点将每一个重构环中的节点编号写成矩阵的形式。若某行支路数目不足,则最大支路数均用0 补齐。

②从第一行随机选取一个非零元素,那么将下一行与之相同的元素置为0,以此类推直到最后一行。

③将步骤②中每行选取的非零元素记为一个1×N的矩阵B,即为一个解向量。

④根据上述的可行解产生的条件3 和条件4,判断步骤③中解向量的分量是否符合条件。 若不符合,则重新在矩阵A中的所在行随机选取。

⑤重复上述步骤,直到得到满足条件的解向量。

3 仿真验证与结果分析

本文使用IEEE 69 节点系统[19-20]及某地区实际配电网[21]作为具体算例,验证所提出的改进粒子群参数协进化和声搜索算法的有效性。 相关算法使用MATLAB 2016a 验证。

3.1 算例1:IEEE 69 节点系统

IEEE 69 节点系统及各节点编号如图3 所示。图3 中,虚线表示5 个联络开关。 当5 个联络开关断开时,造成的网损约为225 kW,最低节点电压为0.909 1 p. u。

图3 IEEE 69 节点系统及各节点编号Fig.3 IEEE 69 node system and node numbers

算法中参数的具体设置为:HSA 中原始种群HM大小为15×5,辅助新和声的和声库选择概率R′HMCR∈[0.95,1],辅助新和声的音调调节概率R′PAR=RPAR,HSA 每次迭代重复次数T=3。 PSO 共生种群大小为15×2,惯性因数w=0.8,学习因子c1=c2=2,作为寻优目标的和声库选择概率区间为RHMCR∈[0.65,0.95],音调调节概率区间RPAR∈[0.25,0.55]。 最大迭代次数为70 次。

重构后的IEEE 69 节点系统网损与最低节点电压如表1 所示。 同时,表1 还包含与本文方法类似的改进和声搜索算法的文献[15]、文献[22],以及其他智能优化算法的文献[21]的重构结果。

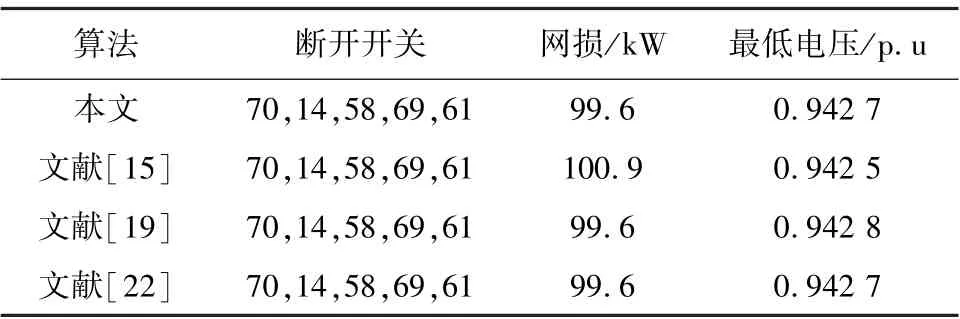
表1 重构后的IEEE 69 节点系统网损与最低节点电压Tab.1 The network loss and minimum node voltage of the reconfigurated IEEE 69 node system

表1 中的开关58,也可以换为55、56 或57。

重构后的IEEE 69 网损降低了55.7%,同时最低节点电压由0.909 1 p.u 提升至0.942 7 p.u。 这一结果与表中的参考文献基本一致,说明了所提出方法能够有效达到降低配电网网损、提升供电质量的目的。

本文使用平均计算次数(平均收敛代数×种群大小)评价性能。 计算次数可以反映算法在寻优过程被调用的次数,以便比较不同方法的优化性能。 算例1 中,本文算法与参考文献算法的性能比较,如表2 所示。

表2 本文算法与参考文献算法的性能比较(算例1)Tab.2 The algorithm performance comparison with the references(Example 1)

由表2 可知,所提出方法以平均计算次数作为评价标准时,在性能方面显著优于文献[22]的改进和声搜索算法;较优于文献[15]的改进和声搜索算法和文献[19]的其他智能优化方法。 在最小收敛代数方面,略逊于文献[15]和文献[19],优于文献[22]。 在寻优成功次数方面优于文献[22],与文献[19]持平,略逊于文献[15]。 综上所述,表1、表2 说明所提出方法以IEEE 69 节点系统作为算例时,可以有效降低配电网网损,与相关参考文献相比具有较好的收敛速度,在寻优成功率上也基本一致。

3.2 算例2:某实际地区配电网

某地区实际配电网及各节点编号如图4 所示。图4 中,虚线表示5 个联络开关。 当5 个联络开关断开时, 造成的网损约为81 kW, 最低节点电压为0.985 0 p.u。

图4 某地区实际配电网及各节点编号Fig.4 Structure and node numbers of a real distribution network in a region

算例2 中,算法的相关参数设置与算例1 中的一致,最大迭代次数为50 次。 重构后的算例2 系统网损与最低节点电压如表3 所示。 同时,表3 也包含与本文方法类似的改进和声搜索算法的数据。

表3 重构后的算例2 系统网损与最低节点电压Tab.3 The network loss and minimum node voltage of the reconfigurated system in Example 2

重构后的算例2 系统网损降低了约9%,最低节点电压由0.985 0 p.u 提升至0.988 7 p.u,与相关参考文献中的结果基本一致,说明所提出方法能够降低配电网网损。

算例2 中,本文算法与参考文献算法的性能比较如表4 所示。

表4 本文算法与参考文献的算法性能比较(算例2)Tab.4 The algorithm performance comparison with the references(Example 2)

由表4 可知,本文算法在平均计算次数方面相对于文献[21]降低了约26%,其余指标与文献[21]的基本一致,表明了本文所提算法在收敛速度上的优势。

4 结论

本文提出一种改进的参数协进化和声搜索算法。考虑到参数协进化和声搜索算法在局部寻优反馈环较长而导致算法计算量增加和收敛性能降低的问题,提出一种辅助新和声策略进行优化。 改进并使用一种自适应音调调节方法,克服和声搜索算法应用于配电网重构时音调调节带宽难以确定的问题。 针对重构过程中出现的不可行解,提出了4 个必要条件进行优化。最后,使用IEEE 69 节点系统和某实际配电网进行了算法有效性与优越性的验证。 验证结果表明,本文所提算法在收敛性能上优于同类别方法的同时,还可以保持较好的寻优性能。