萤火虫算法在三电平NPC 逆变器中的应用

顾 丹

(四川城市职业学院智能制造与交通学院,四川 成都 610000)

0 引言

现代工业技术的发展离不开大功率逆变器的支撑。 中性点箝位型(neutral point clamped,NPC)三电平电路因低谐波畸变率、低器件承受压降和结构简单等优点而被广泛应用[1]。 特定谐波消除脉宽调制(selected harmonic elimination pulse widch modulation,SHEPWM)法作为NPC 拓扑电路常用的调制策略[2],具有直流侧电流纹波小、开关损耗低、能有效消除低次谐波的优点[3]。 SHEPWM 策略的核心在于求解开关角度。 而关于开关角度的方程属于非线性方程组[4],对求解方法具有较高的要求。 文献[5]利用量子遗传算法求解SHEPWM 策略开关角度,提高了求解速度,也为智能算法在SHEPWM 策略中的应用提供了新的解决思路。 本文利用萤火虫算法(firely algorithm,FA)准确、快速的寻优能力,实现了SHEPWM 策略中非线性方程的快速求解,从而准确消除了NPC 逆变器的特定谐波、降低谐波畸变率。

1 SHEPWM 原理分析

SHEPWM 通过计算选取N个开关角度,以实现消除(N-1)个谐波的目的[6]。 SHEPWM 单相输出电压波形如图1 所示。

图1 SHEPWM 单相输出电压波形Fig.1 Single-phase output voltage waveform of SHEPWM

由于三次及三次倍数的谐波在线电压中可抵消,因此主要针对非三倍数的奇次谐波分量进行消除[7]。式(3)展示了消除5、7、11 次谐波的具体表达式。

式中:α1、α2、α3、α4分别为目标方程组的四个开关角度变量;m为基波调制度。

对于式(3)所示的非线性方程组,通常采用同伦算法与牛顿迭代法相结合求解开关角度。 但是该方法计算量大且对初值要求较高,易出现不收敛的情况。因此,本文采用萤火虫算法实现开关角度的求解。

2 FA 的优化

2.1 FA 数学描述

萤火虫作为自然界的一种常见昆虫,其发光的特性引起人们的注意并对其展开研究。 萤火虫发光的主要作用是传递信息,包括异性吸引、警戒、猎物吸引等行为[8]。 基于这一特殊行为,英国学者Yang Xinshe 提出了FA,通过模拟萤火虫的群体行为实现优化[9]。

FA 在萤火虫发光行为的基础上,进一步分析了光信息强度随距离增加而减弱等传播特性,并对FA 提出了以下假设[10]。

①光信息强度与萤火虫个体的性别无关。

②萤火虫个体之间的吸引度与个体距离d成反比,与萤火虫发光亮度成正比;发光亮度越高的个体,越能吸引发光亮度较弱的个体向其聚集。

③发光亮度最高的个体进行随机移动。

根据上述假设,对萤火虫的行为进行数学描述。萤火虫个体i对j的荧光亮度I(dij)如式(4)所示。

式中:dij为营火虫个体i和j之间的距离;Imax为两个萤火虫之间的荧光亮度最大值,此时dij=0;γ为光强吸收系数。

萤火虫i和j之间的相对吸引度β(dij)的数学表达式如式(5)所示。

式中:βmax为两个萤火虫间的最大吸引度。

FA 运行过程中,需要对萤火虫位置进行更新。 令当前时刻t萤火虫i和j的位置分别为xi(t)和xj(t)。当萤火虫i被萤火虫j吸引时,个体i的位置更新如式(6)所示。

2.2 改进的FA

上面介绍的传统的FA 在计算过程的中后期容易出现优化停滞的现象,主要原因在于式(6)中的扰动项不能很好地改善FA 陷入局部最优解的问题;同时,传统FA 还存在极值点附近震荡而导致的收敛速度慢等问题。 针对传统FA 的不足,本文对其进行改进,在提高FA 获得全局最优解的准确性的同时提高其寻优速度。

2.2.1 惯性权重思想的位置更新优化

引入惯性权重实现传统FA 的优化主要体现在对其位置更新步骤的优化。 优化后的位置更新表达式如式(7)所示。

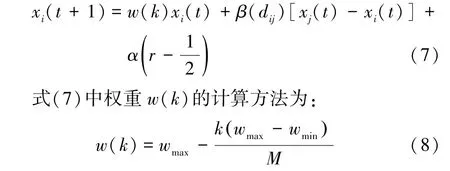
式中:wmax和wmin分别为权重的最大值和最小值;k为FA 的当前迭代次数;M为设定的最大迭代次数。

由式(7)和式(8)可知,权重w(k)的引入能够改变萤火虫个体当前时刻位置对下一时刻位置变化的影响程度。 其影响表现为在FA 的运行初期能够提高算法的全局搜索能力,进而加快算法的寻优速度。 随着算法的不断进行,权重w(k)值不断减小,使得萤火虫个体的移动距离减小。 对此,增加局部区域的搜索力度,从而避免在极值附近产生震动。

2.2.2 最优个体更新策略改进

传统的FA 在确定亮度最高的萤火虫个体后,命令其余个体向该最优个体移动。 但是在该步骤的进行过程中没有考虑到最优个体是否陷入局部最优解或是否为真正的最优解个体。 因此,本文视已确定的最优萤火虫个体为准最优解个体Pbest(t),对其增加随机运动操作,进一步判断最优个体值。 该随机运动操作采取高斯扰动策略,使其在有效空间内作随机运动,得到最优个体,记作P′best(t),如式(9)所示。

基于位置更新优化和最优个体更新策略对传统的FA 进行改进,可以有效地提高FA 的寻优速度,增强其避免陷入局部最优解的性能。

3 基于改进FA 的SHEPWM 策略

利用改进的FA 求解SHEPWM 的开关角度问题时,需先将式(3)所示的非线性方程组转化为目标优化问题。 式(3)中的每个子方程均可被视为一个优化目标函数,分别记为h1、h2、h3、h4。 将上述4 个具有联系的多目标函数转化为单目标函数,如式(11)所示。以minH作为改进的FA 的适应度函数,使其值最小,获得SHEPWM 的开关角度α1、α2、α3、α4值。 若求解结果中有多组可行解时,以总谐波失真(toatal harmonic distortion,THD)最小为判断依据确定开关角度值。

改进FA 求解SHEPWM 策略流程如图2 所示。

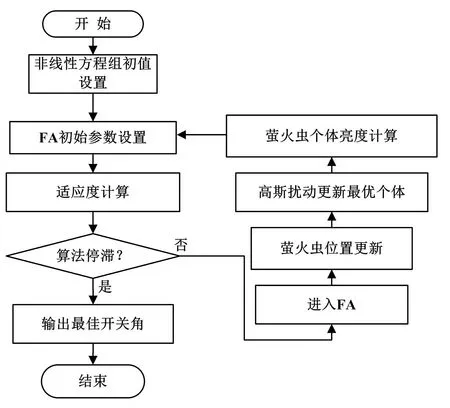
图2 改进FA 求解SHEPWM 策略流程图Fig.2 Flowchart of SHEPWM solving by advanced FA

4 仿真验证及结果分析

利用MATLAB 仿真改进的FA 求解SHEPWM 的开关角度以及NPC 三电平逆变器的输出电压。 NPC电路的参数设置为:直流侧电压Udc=300 V,负载为感性负载,三相负载电阻和电感值分别为10 Ω 和2 mH,调制度m=1;改进的FA 的参数设置为:萤火虫种群个数为50,最大迭代次数为300,γ=0.6,Imax=10,dij的初始值为0.3,α=0.07,βmax=0.1,迭代误差精度为10-3。

为验证改进的FA 在收敛速度和精度上的提升,图3 展示了分别在FA 和改进FA 的作用下求解SHEPWM 开关角度时的适应度值。

图3 两种算法的适应度值Fig.3 Fitness values of the two algorithms

以THD 最低为开关角度最优解的选择依据,改进的FA 得 到 开 关 角 度α1、α2、α3、α4值 分 别 为19.100 6°、46.538 8°、52.580 9°、85.450 8°,THD 值为15.3%;传统的FA 得到的开关角度值分别为:14.225 1°、63.348 9°、67.886 8°、83.579 2°,THD 值为16.5%。 该结果说明改进的FA 得到的最优解优于传统FA。

图4 和图5 分别为改进的FA 作用下的三电平NPC 线电压输出波形及其谐波频谱分析。

图4 线电压输出波形Fig.4 Line voltage output waveform

图5 线电压谐波频谱分析Fig.5 Harmonic spectrum analysis of line voltage

由图5 可知,线电压的输出波形中已无5 次、7 次和11 次谐波成分。 这一方面说明改进的FA 求得的最优解能够有效地消除特定的谐波成分,充分改善了三电平NPC 逆变器的输出电压质量,另一方面也说明该方法应用于SHEPWM 策略求解中的有效性和准确性。

5 结论

通过对广泛应用于三电平NPC 逆变器中的SHEPWM 策略原理进行分析,确定将开关角度求取作为SHEPWM 策略的主要研究方向,并引入萤火虫算法用于求解开关角度,同时对传统萤火虫算法位置更新以及最优个体更新策略进行改进。 为验证改进的萤火虫算法的有效性,对SHEPWM 策略进行仿真验证。 验证结果表明,改进的萤火虫算法具有更快的收敛速度以及更好的全局最优解的求解能力,可有效消除特定次数的谐波成分,降低了三电平NPC 逆变器输出电压的谐波畸变率。