大跨度斜拉扣挂悬臂浇筑混凝土拱桥施工期抖振响应分析

张基进 郭吉平 刘 杰

（贵州路桥集团有限公司，贵阳550001）

0 引 言

拱桥因其合理的受力形式、美观性、良好的耐久性备受工程师们的青睐，并且随着理论研究和施工工艺的发展，拱桥跨度不断增加。随着跨度的增大，拱桥呈现出轻柔、低频的力学特征，导致桥梁对风的作用更加敏感，其中抖振响应分析已经成为抗风设计中的重要环节［1］。抖振是一种限幅振动，它虽不像颤振那样引起灾难性的失稳破坏，但是可使桥梁不能正常运营，在抖振响应过大的情况下还会引起桥梁结构的局部疲劳［2］。针对拱桥抖振分析，晏致涛等［3］提出了分析大跨度中承式拱桥抖振的时域和频域方法；张亮亮等［4］分析了山区复杂山地风作用下钢桁架特大拱桥的抖振响应。目前关于拱桥抖振的研究工作很多，但是确少有对于采用斜拉扣挂悬臂浇筑施工的特大拱桥的抖振分析。斜拉扣挂施工方法是拱桥主拱圈施工方法中较为常见的一种。采用这种施工方法时，主拱圈在悬臂施工阶段刚度较小，在风荷载作用下易产生较大振动，所以有必要对此种施工方法下的结构进行抖振分析。

本文结合贵州某采用斜拉扣挂悬臂浇筑法施工的特大拱桥，针对裸拱最大悬臂状态，运用有限元软件建立施工期模型，采用谐波合成法模拟脉动风荷载，基于APDL语言编制抖振时域分析程序，计算并分析结构抖振响应。

1 工程概况

某桥跨越乌江，上部结构为6×30 m T梁+240 m钢筋混凝土箱形拱桥+6×30 m T梁，设计速度40 km/h，桥面宽20 m，双向4车道，设计汽车荷载等级采用公路-Ⅰ级，主拱圈采用悬臂浇筑施工工艺，在采用悬臂浇筑工艺的同类型桥梁中位居国内第一、亚洲第二。主拱圈为等高度悬链线钢筋混凝土箱形截面，截面宽10 m、高4.5 m。拱圈纵向共分为37个节段，其中两岸拱脚位置1号节段为支架现浇段，拱顶设一个吊架浇筑合龙段，其余34个节段为悬浇段，大桥立面及施工扣锚索总体布置如图1所示。

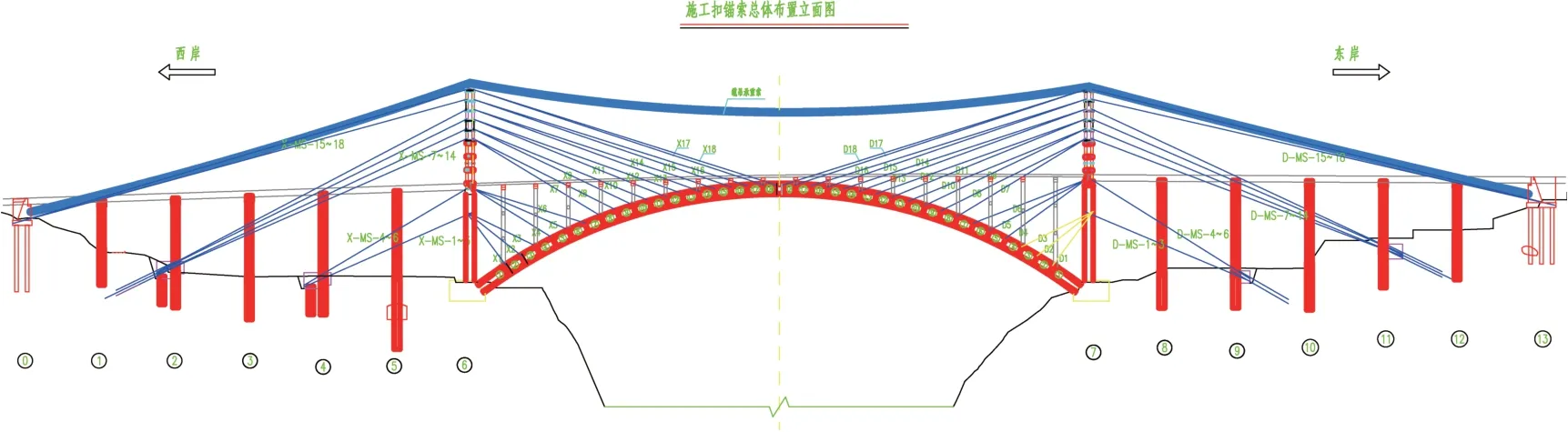
图1 施工扣锚索总体布置立面图Fig.1 Elevation view of anchor cables during construction

2 动力特性分析

2.1 有限元模型

采用离散结构的有限元方法对大桥施工最不利阶段（裸拱最大悬臂状态）进行结构建模，其中主拱及桥塔采用梁单元模拟，扣锚索采用link单元模拟。主拱及扣塔底部固结。动力特性分析使用的有限元计算模型如图2所示。

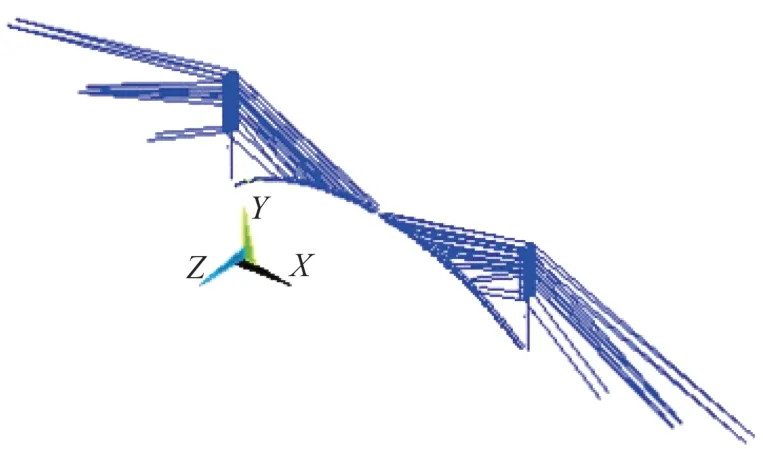
图2 有限元模型Fig.2 Finite element model

2.2 动力特性分析结果

裸拱最大悬臂状态下的动力特性分析主要结果如表1所示，从表1中可以看出，裸拱最大悬臂状态下结构频率较低，在悬臂施工阶段刚度较小，进行风致动力响应分析是必要的。

表1 裸拱最大悬臂状态动力特性分析结果Table 1 Dynamic analysis results of the bare arch during the maximum cantilever stage

3 脉动风场模拟

3.1 脉动风特性

影响风场模拟的重要因素有风谱模型、空间相关函数和气动导纳函数。这些参数的选用对风场模拟和结构风致振动响应有着关键性的影响。风场模拟的首要任务是选取合适的风谱模型，它由功率谱密度函数（PSD）表示。参照抗风规范，纵向脉动风速谱选用Kaimal谱，竖向脉动风速谱选用Lumley-Panofsky谱。

式中：f为无量纲量，称为莫宁坐标或相似律坐标，f=nz/U(z)；z为离地面高度；U（z）为高度z处的平均风速；u*=K U(z)/ln[(z-zd)/z0]，u*为摩擦风速，与地面粗糙长度相关；zd=Hˉ-z0/K，Hˉ为周围建筑物平均高度（m），K≈0.4，z0为地面粗糙长度。

不同空间位置的点，用互功率谱密度函数（CSD）反映风速时程的相关性。空间相距r的任意两点，其脉动风速i分量（i=u，v，w）的空间相关性采用互功率谱密度函数表示为

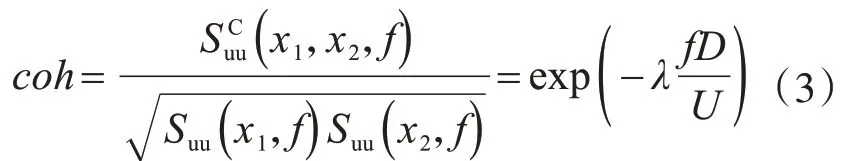
式中：Suu(x1，f)为纵向脉动分量u在x1处的功率谱；为纵向脉动分量u在x1处与x2处互谱的实部；λ为衰减因子；f为风的频率；D为x1与x2之间的距离；U为平均风速。

可见，该相关函数是两点距离的衰减函数，λ反映了衰减速度。λ直接影响到风场模拟和结构风致振动响应的真实性，参照抗风规范，本文x、y、z方向的λ分别取为7、10、16。

3.2 风场拟合

本文风场模拟选取风速点共52个，其中主拱32个，扣塔20个，主拱沿纵向平均4 m一个风速点，扣塔沿竖向平均4 m一个风速点。根据谐波合成法原理，通过计算软件编制脉动风模拟程序，其中，1号、20号、50号点的脉动时程图如图3所示。取1号点为检验点，对模拟结果进行分析。图4为1号点脉动风样本的功率谱密度与目标函数功率谱密度的吻合图，由图中可以看出模拟出的脉动风准确可靠［5］。

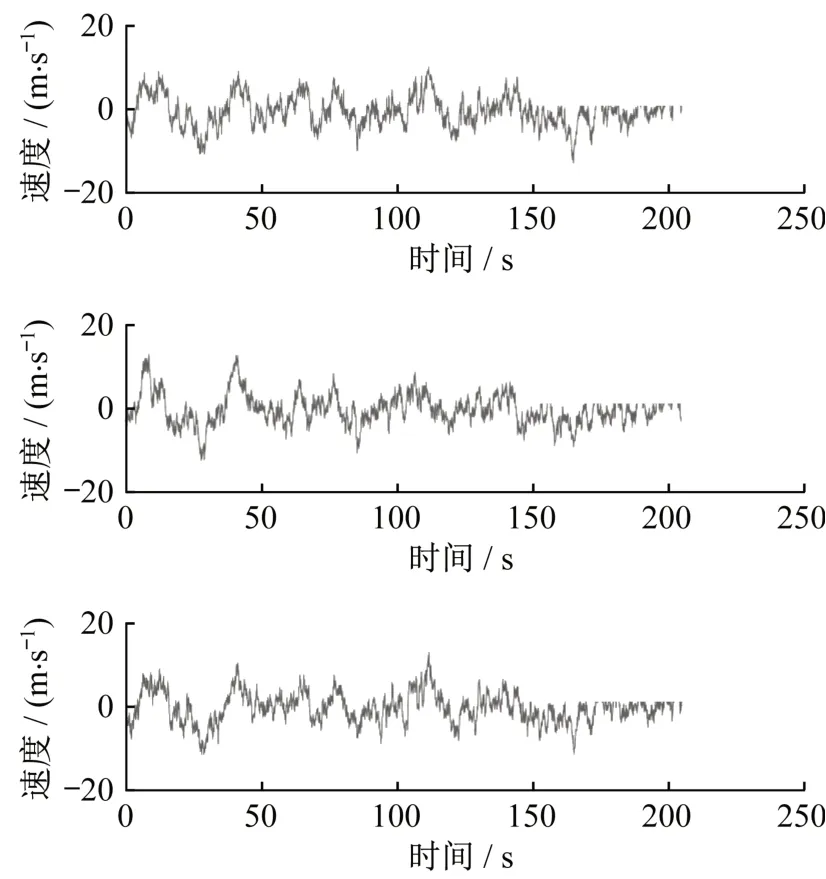
图3 模拟的风速时程曲线Fig.3 Simulated wind speed time series

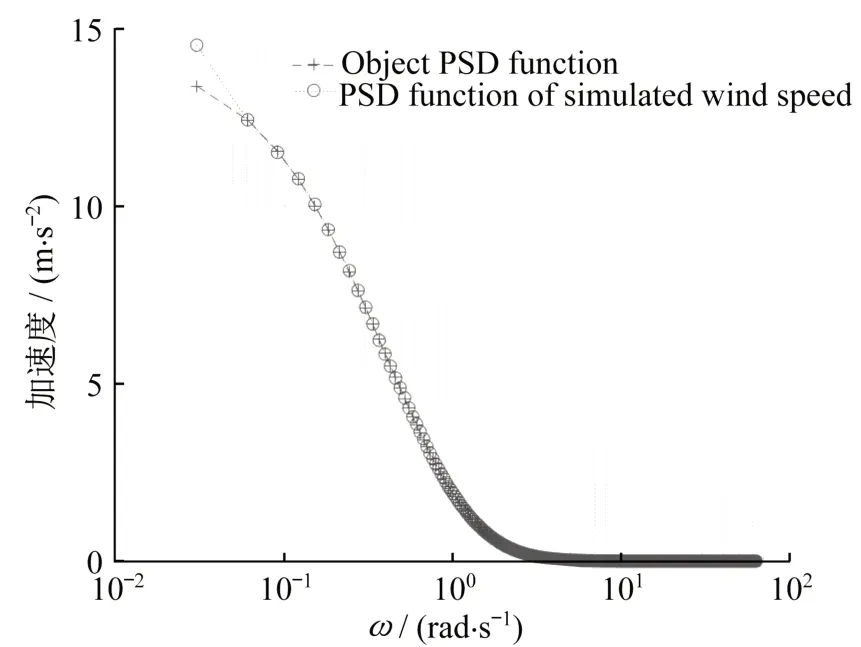
图4 目标功率谱及拟合功率谱Fig.4 Objective and simulated power spectrums

4 主桥最不利施工状态抖振分析

4.1 主拱静力三分力系数识别

主拱静力三分力数值识别的意义在于为桥梁施工阶段的风致响应计算分析提供气动力参数［6］。通过数值风洞模拟主拱断面的气动阻力系数、升力系数和扭矩系数三个分量，参考尺寸取主拱断面宽10 m、高4.5 m。风攻角考虑0°、±1°、±3°、±5°、±7°、±9°、±11°、±13°。由于主拱断面为上下对称结构，故只需模拟正攻角的参数，负攻角的结果可通过对称性直接获取。主拱在体轴系下三分力随风攻角的变化曲线如图5所示。由图5可以看出，主拱的扭矩系数在±13°风攻角范围内，数值都接近于零，说明结构不存在发生静风扭转失稳的危险。

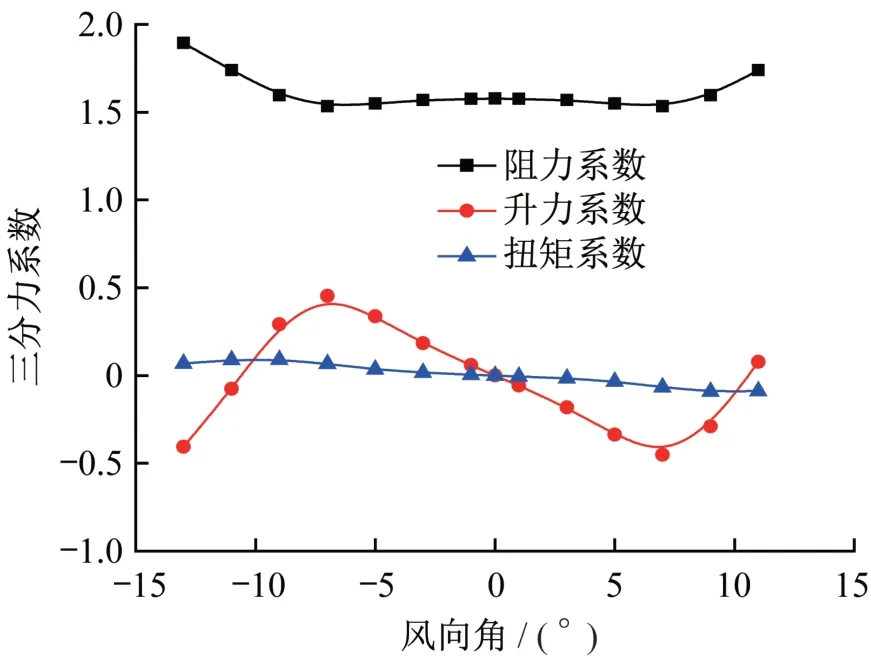
图5 主拱不同角度下三分力系数曲线（体轴）Fig.5 The coefficient of tri-component of the main arch at different wind attack angles

5.2 计算结果

本文分析了主拱最大悬臂状态下，在10 m高度 处 风 速 分 别 为2 m/s、6 m/s、10 m/s、14 m/s、16 m/s、18 m/s、20 m/s、22 m/s、23 m/s、24.2 m/s 10种工况下的抖振响应，在不同风速下的抖振响应结果：主拱跨中位移如图6所示，扣塔顶位移如图7所示，拱脚内力如图8所示，塔根在不同风速下的抖振响应内力如图9所示。从图中可以看出：

图6 主拱跨中在不同风速下的抖振响应位移Fig.6 The buffeting displacements at mid-span of the main arch on different wind speeds

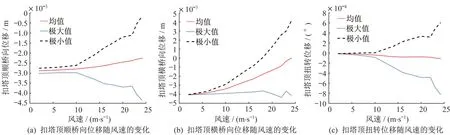
图7 扣塔顶在不同风速下的抖振响应位移Fig.7 The buffeting displacements at the top of tower on different wind speeds

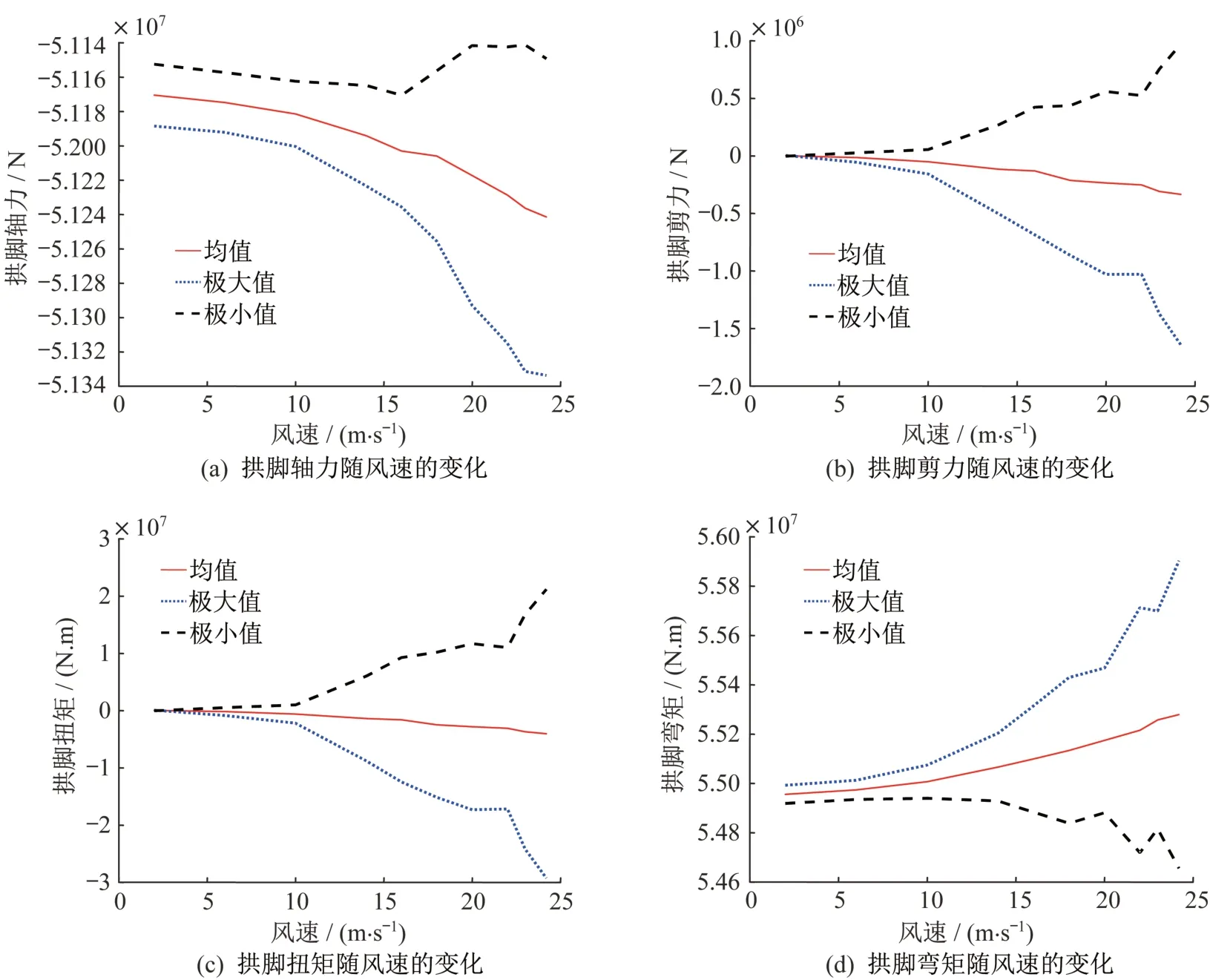
图8 拱脚在不同风速下的抖振响应内力Fig.8 The buffeting displacements at arch foot on different wind speeds

图9 塔根在不同风速下的抖振响应内力Fig.9 The buffeting displacements at the bottom of tower on different wind speeds

（1）随着风速的增大，结构的抖振响应极值越来越大。

（2）主拱跨中竖向、侧向、扭转位移及扣塔顶扭转位移均值随风速增加而增大，扣塔顶顺桥向及横桥向位移均值随风速增加而减小。

（3）除塔根剪力外，其余内力响应随风速增加均未发生大幅度变化。

（4）施工期最不利状态的拱桥抖振响应，以10 m高度处风速24.2 m/s为例，主拱跨中抖振竖向位移均值5 mm，侧向位移响应均值20.8 mm，扭转位移响应均值5×10-5°。拱脚弯矩均值55 270 kN·m，塔根弯矩均值26 640 kN·m。

5 结 论

为研究大跨径拱桥施工状态下的抖振响应，分析施工过程中拱桥的抗风性能，合理评判施工期受风安全性，预防重大事故发生，本文针对某采用斜拉扣挂悬臂浇筑施工的特大拱桥，开展了施工最不利状态下的风致抖振响应研究。

首先采用离散结构的有限元方法对大桥施工最不利阶段（裸拱最大悬臂状态）进行结构建模，对拱桥施工期的结构动力特性进行了分析，然后采用谐波合成方法模拟桥梁各空间点的纵向和竖向脉动风速样本，通过对模拟的风速时程曲线进行相关性检验，验证了模拟脉动风场的适用性和准确性，最后对拱桥施工最大悬臂状态进行了时域抖振计算分析，得到了结构关键部位在抖振作用下的内力和变形响应。研究结果可为该桥施工期受风安全性分析提供依据，为同类型的桥梁结构抗风设计提供参考。