粒子加速器电源PID控制方式的改进型研究与应用

卢军祥 ，马保慧 ，柳恒敏 ，陈改霞 ，蔺满强

（1.天水电气传动研究所集团有限公司，甘肃 天水 741020；2.大型电气传动系统与装备技术国家重点实验室，甘肃 天水 741020）

PID控制是将给定量与反馈量相减形成偏差信号e（t），通过对偏差信号e（t）进行比例P（proportional）、积分(Integral）、微分D(Derivative)运算后形成的一种控制规律。达到“利用偏差，消除偏差”的目的。粒子加速器电源控制器在原有传统PID控制方法的基础上，将传统PID控制方法中的微分项进行改进，形成三个微分项系数kd1、kd2、kd3，通过对微分项系数kd1、kd2、kd3参数调整选择调节器为PI调节器或PID调节器，同时，在PID调节器中引入一阶惯性环节，形成不完全微分PID算法，引入惯性系数kt1和kt2，通过对惯性系数kt1和kt2的参数调整来实现粒子加速器电源调节器算法为普通PID算法或不完全微分PID算法。

1 PID控制方式在粒子加速器电源模拟调节器中的研究与应用

首先，我们对模拟PID调节器进行计算与分析，粒子加速器电源模拟PID调节器如图1所示：

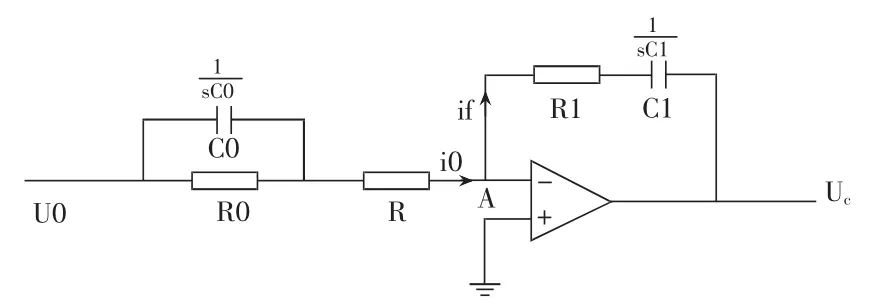
图1 模拟PID调节器

1.1 模拟PID调节器微分方程与传递函数计算与分析

（1）设电容C0上的电压为UCO，电流为iC0,则电容C0上的电压与电流关系为：

将上式进行拉普拉斯变换为：

（2）R0与C0并联部分的阻抗为：

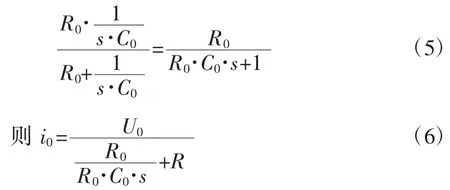
（3）运放反馈环节电压与电流关系为：

（4）运放深度负反馈，则运放输入端内阻无穷大，输入电流近似为0，即“虚短”。

则电流i0＝if

结合式（6）与式（7）得：

系统传递函数为输出量与输入量的比值，即

将式（8）写成传递函数的形式为：

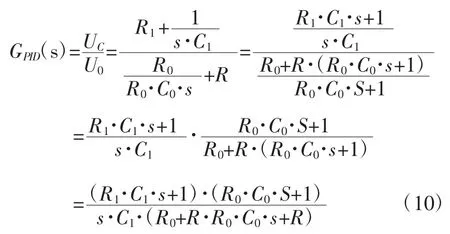
将上式分子分母同乘以R1得:

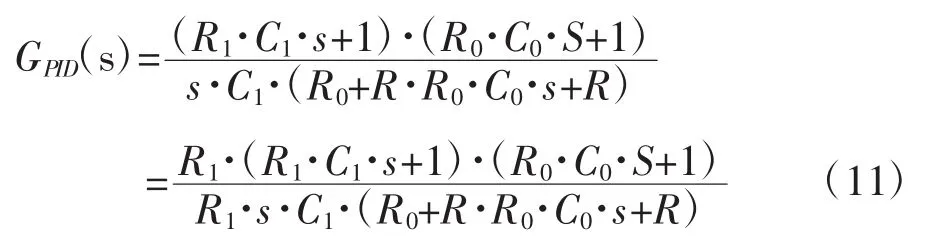
将式（11）的分母项单独提取出来进行变换，式（11）分母项为

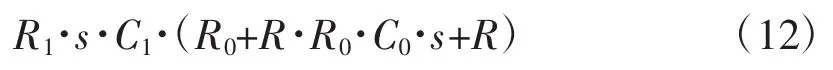
将式（12）乘以（R0+R）后，再用（R0＋R·R0·C0·s＋R）除以（R0+R）,原式值保持不变。

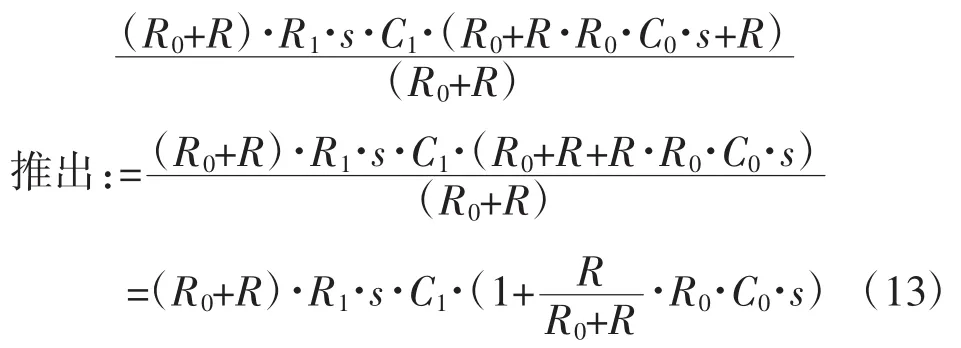
将式（13）带入式（11），得：

则式（14）可写为：

则上式为图1的PID控制器传递函数。

1.2 模拟PID调节器传递函数分析

式（16）为图1模拟PID调节器的传递函数，PID调节器的输入量为Ur（s）,输出量为UC（s）则：

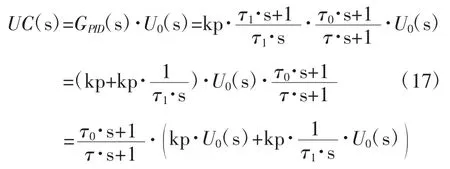
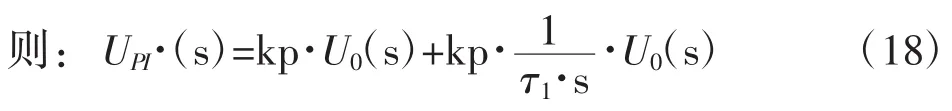
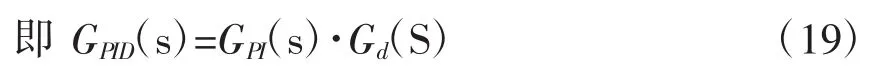
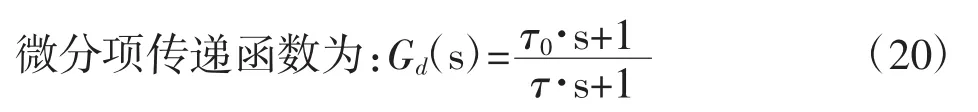
1.3 模拟PID调节器参数调整与应用

积分项的系数为：τ1＝R1·C1，即积分时间常数的调整可以通过调整电阻R1的阻值与电容C1的容值来进行调整。

1.4 模拟PID调节器的改进与应用

微分作用的引入使系统能够根据偏差变化的趋势做出反应，适当的微分作用可加快系统响应，有效地减小超调，改善系统的动态特性，增强系统的稳定性。不利之处是微分作用对干扰敏感，使系统抑制干扰能力降低。因此，我们在粒子加速器电源模拟调节器实际应用中，不对偏差信号e（t）进行微分，而是将偏差信号中的反馈量Uf进行微分，即采用微分负反馈形式。微分反馈的特点是：在稳态时，输出量不发生变化，其微商将为零（即du/dt=0），于是微分反馈支路电流为0，微分反馈不起作用，当输出量随时间发生变化时，便起反馈作用，而且输出量变化率越大，这种反馈作用越强［1］。即微分负反馈只在动态过程中起作用，而在稳态中不起作用，于是我们在实际应用中将对偏差信号e（t）的微分改为对反馈信号Uf的微分,如图2 Uf反馈支路所示，此时，PID调节器变为PI调节器与微分负反馈校正的结合，同时，引入一阶惯性环节，电容C104为构成惯性环节的电容。Ur给定支路与Uf反馈支路构成加法电路。Ur与Uf的差值为偏差信号e（t）。电阻R105为差分放大电路平衡电阻。采用PI调节器后，由于运放反馈回路中串有电容器C105与C104，因此，在稳态时，运放反馈回路相当于断路，运放零点漂移的影响很大，所以在运放反馈回路两端再并联一个反馈电阻R107，R107一般取2-4M，以使零漂引起的输出电压的波动受到运放负反馈的抑制。电阻R101、R102与电容C101构成T型滤波网络，对给定信号Ur进行滤波，同样，电阻R103、电阻R104与电容C102构成T型滤波网络，对反馈信号Uf进行滤波。

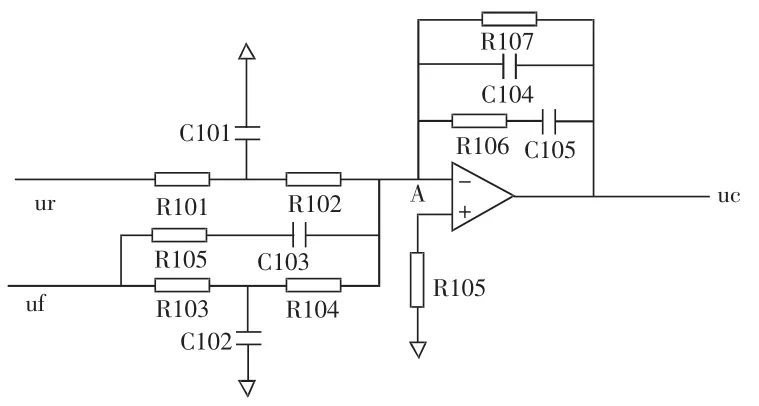
图2 实际使用的模拟PID调节器

2 PID控制方式在粒子加速器电源数字调节器中的研究与应用

2.1 传递函数的Z变换

式（17）分为比例积分合微分两部分，将其用Z变换表示：

依据拉普拉斯与Z变换表可查得：

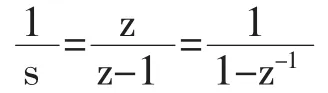
则将UPI（s）进行Z变换为：

将Ud（s）进行Z变换为：

其中Ts表示采样时间。

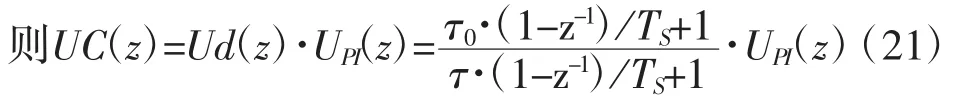
2.2 通过微分系数参数调整实现粒子加速器电源数字调节器的类型选择

从式（17）、式（18）、式（20）可知：

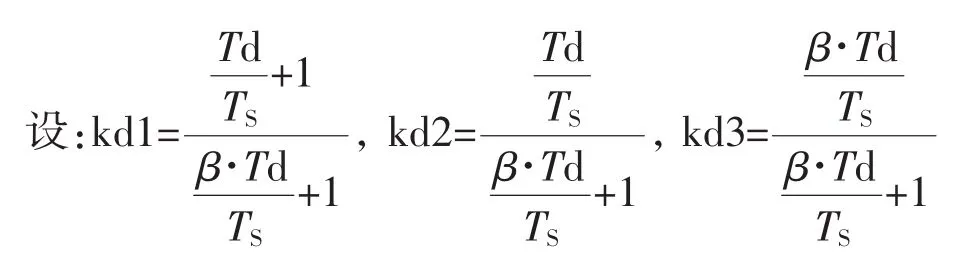
则式（23）可表示为：

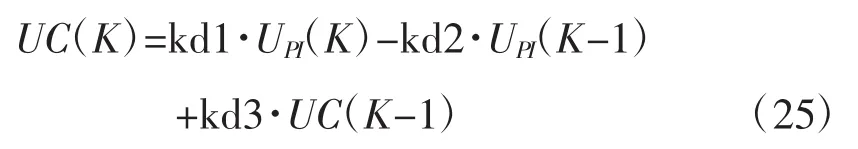
当Td=0，即微分时间常数等于0时，Kd1=1，kd2=0，kd3=0，

此时：UC（K）＝UPI（K）UC（K）的值仅为比例积分部分的值，即调节器为PI调节器，当Td不等于0时，即微分时间常数不为0时，调节器为PID调节器。

这里可以利用对微分部分参数的正确设置来屏蔽微分作用，即可以选择调节器为PI调节器或PID调节器，达到了通过对微分系数参数调整实现数字调节器的类型选择的目的。

2.3 基于不完全微分PID算法的粒子加速器电源数字调节器

在PID控制中，微分信号的引入可以改善系统的动态特性，但也易引入高频干扰，在误差扰动突变的时候尤其显出微分项的不足。要解决这个问题，可以在控制算法中加入低通滤波器，方法之一是在PID算法中加入一个一阶惯性环节（低通滤波器）可使得系统的性能得到改善。这种在普通PID算法的基础上引入一阶惯性环节的PID算法叫做不完全微分PID算法［3］。

粒子加速器电源PID数字调节器在整个PID算法后串联了一个一阶惯性环节，

一阶惯性环节传递函数为：

不完全微分PID调节器可表示为：

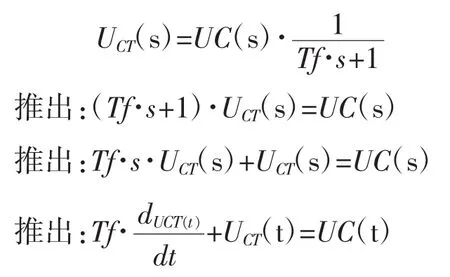
微分用后项差分代替，得：

则式（26）可表示为：

当Tf=0，即惯性时间常数为0时，kt1=1，kt2=0，UCT（k）＝UC（k）

粒子加速器电源数字调节器算法为普通PID算法。

当Tf≠0，即惯性时间常数不为0时，UCT（k）＝kt1·UC（k）＋kt2·UCT（k－1）

粒子加速器电源数字调节器算法为不完全微分PID算法。

这样，我们可以利用对一阶惯性环节参数kt1、kt2的正确设置来选择粒子加速器电源数字调节器为普通PID算法还是不完全微分算法。

2.4 粒子加速器电源PID数字调节器的FPGA实现

式（28）为PI调节器的差分方程。

式（25）为普通PID调节器的差分方程，其表示形式如下：

UC（k）＝kd1·UPI（K）－kd2·UPI（K－1）＋kd3·UC（k－1）

式（27）为不完全微分PID调节器的差分方程，其表示形式如下：

UCT（k）＝kt1·UC（k）＋kt2·UCT（k－1）

结合式（28）、式（25）、式（27）的差分方程画出在FPGA中实现粒子加速器电源数字调节器的流程框图如图3所示。

图3 FPGA中实现粒子加速器电源数字调节器的流程图

图3中，U0（k）为偏差信号，即给定-反馈；Kp为比例项系数；Ki为积分项系数；Kd1为微分项系数1；Kd2为微分项系数2；Kd3为微分项系数3；Kt1为惯性项系数1；Kt2为惯性项系数2；Kp_limit为比例限幅；Ki_limit为积分限幅。

粒子加速器电源的调节器需要有很高的控制精度，故数字调节器的FPGA实现采用了基于浮点数的运算方式。在FPGA中，设计了浮点数加法器、浮点数乘法器、浮点数比较器，则图3中加法选用浮点数加法器来实现，浮点数加法器有方向选择端，可通过方向选择端来设定加法器进行加法运算或减法运算；乘法使用浮点数乘法器来实现；比例限幅与积分限幅功能通过比较器来实现。各运算单元分时复用，采用流水线方式进行运算。

3 结论

目前模拟调节器PID改进型控制方式已经在我公司为某研究所设计的实验环二极铁电源上得到了应用，经过两年的长期运行，运行可靠稳定，完成了模拟调节器的设计目标，同时设计了微分项系数与惯性项系数参数可调的粒子加速器电源数字PID调节器。目前该数字调节器已在我公司生产的粒子加速器数字电源中得到了广泛的应用。基于数字控制方式的灵活性，只需微小修改数字调节器FPGA的设计，就可以使数字调节器适用于更多类型的电源需求，该设计降低了成本，提高了可移植性，达到了良好的使用效果。