混合风险厌恶下预防性努力投资决策
杜景南,黄德春,程 文
(1.河海大学商学院,江苏南京 211100; 2.中国华融资产管理股份有限公司,北京 100033)
一、引 言
基于预防性努力的投资决策是规避金融风险的重要行为,Ehrlich等的开创性工作提出个体的自我预防性投资决策问题,他们从自我保险问题中分离出预防性投资问题并对其进行经济学分析[1]。预防性投资降低坏的事件结果或财富损失事件发生的概率,同时也提高好的事件结果发生的概率,而且预防性投资减少所有发生的损失结果的大小。预防性投资的经济模型考虑的是减少坏的事件发生概率所获得的收益与减少所有事件结果效用的成本之间的权衡。在风险决策理论中,预防性投资是风险管理的基本策略之一。Courbage等分析背景风险的各种配置策略,并且在两期模型里对个体的预防活动建立数学模型,论证个体的最优预防行为与背景风险的特性和效用函数的性质有关[2]。Menegatti讨论背景风险和自我保护努力投资之间的联系,并且论证如果个体的风险偏好是谨慎的,那么在引入具有可加性的背景风险时会增大个体自我保护努力投资[3]。田国强等对当前高阶风险厌恶理论的前沿发展、实验证据以及相关应用进行了梳理和评述[4]。在一维效用模型里,Eeckhoudt 等提出关于个体支出预防费用以减小损失风险发生的概率的两期模型,并且导出独立的背景风险的引入或恶化将会使他增加其预防性投资的个体风险偏好条件[5]。田有功等验证了更加风险厌恶的个体总是投资更多的预防性努力活动[6]。基于Jindapon等的建模方法[7],Chuang 等分析个体付出努力增加好的风险分布的概率的情况,他们的研究结果表明:当个体努力的成本是非货币时,他做出更多的努力投资;当个体的努力成本是货币时,将会产生更多的努力投资行为[8](1)笔者采用经济学中期望效用理论反映决策者的风险偏好特征。。
此次研究目的是在二维风险模型里,分析个体的二维风险厌恶和相关性风险厌恶行为对个体的最优预防决策的影响。首先,值得注意的是学者前期的工作是在具有一个参数的效用函数的框架里进行的。然而,因经济环境的多维度性,即个体面临几种来源的风险并且他的效用依赖于几种指标如财富变量和背景变量。在二维效用模型里,笔者分析个体的二维混合风险厌恶行为对其努力投资决策的影响。其次,大多数学者已经注意到背景风险在个体的努力投资决策问题的研究中的作用,但是他们通常将财富风险和背景风险视为相互独立的关系。笔者将相关性风险厌恶行为引入到对个体的努力投资决策的研究中。再次,笔者观察到经济系统的变化通常包含一些变量的同时不确定性因素。最后,使用具有风险相关性结构的4-状态抽奖模型,笔者讨论个体的相关性背景风险厌恶行为对其努力投资决策的影响。
二、风险相关性和混合风险厌恶
首先给出风险相关性结构和相关性厌恶(correlation aversion)的概念,并推导关于决策者的风险偏好的初步结论。
设二维von Neumann-Morgenstern效用函数u(x,y),(x,y)∈[a,b]×[c,d]表示决策者的风险偏好。假定对任意的非负整数k1和k2,函数u(x,y)的所有偏导数u(k1,k2)(x,y)= ∂k1+k2u(x,y)/∂xk1∂yk2存在并且是连续的。给定两个相互独立的随机变量X∈[a,b]和Y∈[c,d],存在如下定理:
定理1下列的陈述是等价的:
(a)对独立的风险X和Y,不等式Eu(X,Y)≤Eu(X,EY)成立;
(b)对∀(x,y),u(0,2)(x,y)≤0。
定理1表明决策者对Y≤0是风险厌恶的,当且仅当二维效用函数u在它的第二个属性上是凹的,即u(0,2)≤0。
当这两种风险是依赖的和局部时,笔者首先获得如下定理:
定理2对于局部的风险X和Y,并且Cov(X,Y)≥0,如果u(0,2)(x,y)≤0和u(1,1)(x,y)≤0,∀(x,y), 那么不等式Eu(X,Y)≤Eu(X,EY)成立。
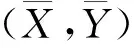
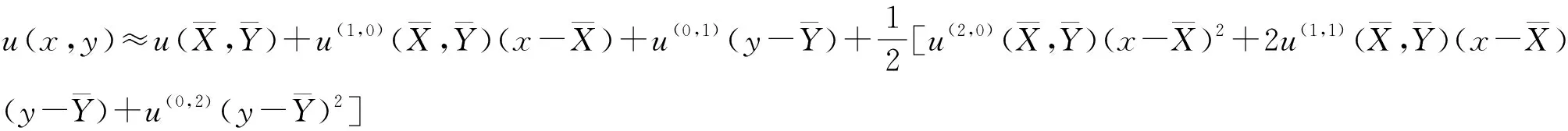
(1)
由Taylor近似(1)可得
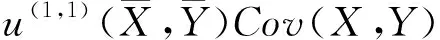
(2)
这里,Var(·)和Cov((·,·)分别是方差和协方差算子。由近似式(2),可得出对于Cov(X,Y)≥0的局部风险X和Y,如果u(0,2)≤0和u(1,1)≤0,那么Eu(X,Y)≤Eu(X,EY)。
Eeckhoudt等将u(1,1)≤0解释为决策者是“相关性厌恶”的充要条件,指y越大则可以减轻对x降低的不利的影响[9]。定理2表明,当两种局部的风险是正相关时,如果决策者在y上是风险厌恶的(u(0,2)≤0)和相关性厌恶的(u(1,1)≤0),那么他对Y是风险厌恶的。
对于两种依赖的局部风险的情况,笔者得出如下定理:
定理3对于Cov(X,Y)≥0的依赖的局部风险X和Y,如果u(0,2)(x,y)≤0,u(2,0)(x,y)≤0和u(1,1)(x,y)≤0,∀(x,y), 那么不等式Eu(X,Y)≤u(EX,EY)成立。
证明:由在定理2的证明中效用函数u(x,y)的Taylor近似(1)可得:
上式推出对于Cov(X,Y)≥0的局部风险X和Y,如满足u(0,2)≤u(2,0)≤0和u(1,1)≤0,那么Eu(X,Y)≤u(EX,EY)。
定理3表明,对于具有正相关性的两种局部风险,如果决策者在x上是风险厌恶的u(2,0)≤0,在y上是风险厌恶的u(0,2)≤0以及相关性厌恶的u(1,1)≤0,那么他对(X,Y)是风险厌恶的。
考虑对具有更强相关性的任何两种风险的风险厌恶的情况。设F(x,y)表示X和Y的联合分布,FX(x)和FY(y)分别表示它们的边际分布。Lehmann[10]定义下列的变量随机依赖的概念:
定义1 如果F(x,y)≥FX(x)FY(y),∀x,y,那么二维风险(X,Y)是正象限依赖的,记为PQD(X,Y)。
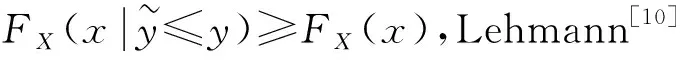
定理4下列的表达是等价的:
(a)对于PQD(X,Y),不等式Eu(X,Y)≤u(EX,EY)成立;
(b)对∀(x,y),u(0,2)(x,y)≤0,u(2,0)(x,y)≤0和u(1,1)(x,y)≤0。
定理4揭示对于POD(X,Y),决策者对(X,Y)是风险厌恶的当且仅当他在x上是风险厌恶的(u(2,0)≤0),在y上是风险厌恶的(u(0,2)≤0)以及是相关性厌恶的(u(1,1)≤0)。Li(2011)指出对于(POD)风险,效用函数负的混合导数是控制相关性影响的必要条件。
三、努力的非货币成本模型
根据Chuang等[8]的基本模型,笔者在多个风险的框架下对决策者的努力投资决策问题建模。考虑两种来源的风险指标:一种是内生的财富或收入的随机性风险,称之为金融风险;另一种是外生的背景变量的风险,即非金融风险或背景风险。
首先分析决策者具有非货币努力成本的情形。设θ(e)表示努力e的成本函数(效用度量),并且θ(0)=0,θ′(e)≥0和θ″(e)≥0。决策者选择努力水平e,为了最大化他的期望效用:
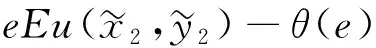
(3)
最大化问题(3)相应的FOC(一阶条件)是
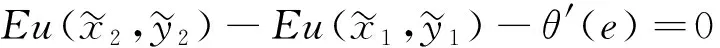
(4)

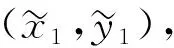
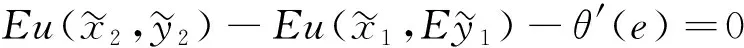
(5)
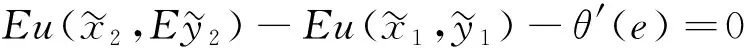
(6)
当两种风险是相互独立时,由Courbage等研究在独立风险的情况下预防性储蓄的方法[2],获得下列命题:
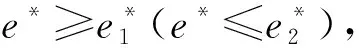
证明:关于初始背景变量指标的不确定的影响,由(5)和优化问题的凹性可得
关于最终背景变量指标的不确定的影响,由(6)和目标问题的凹性可得
命题1的解释是显而易见的。当财富风险和背景风险是相互独立时,对于背景变量风险厌恶(u(0,2)≤0)的决策者,引入初始(目标)背景变量指标的不确定性会增大(减小)决策者努力的边际收益而不改变他的边际成本。因此这样的决策者将会付出更多(更少)的努力投资。
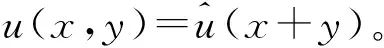
当两种风险不是相互依赖的并是局部的风险,根据在两种局部的风险的情况下Menegatti[3]研究预防性储蓄问题的方法,笔者获得命题如下:
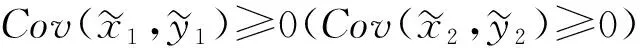
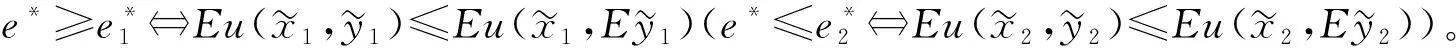
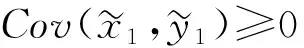
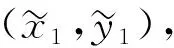
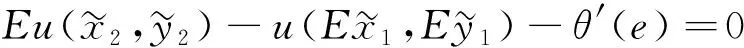
(7)
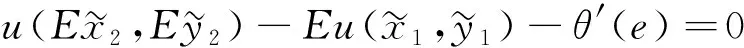
(8)
当两种风险是依赖的和局部的,与Menegatti[3]的预防性储蓄的分析类似,笔者得到下面的命题:
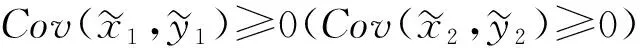
证明:对于初始目标的两种变量指标的不确定的联合影响,由(7)和优化问题的凹性可得:
对于最终目标的两种变量的不确定的联合影响,由(8)和优化问题的凹性可得:
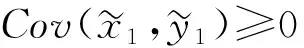
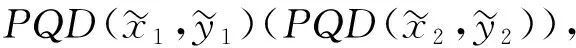
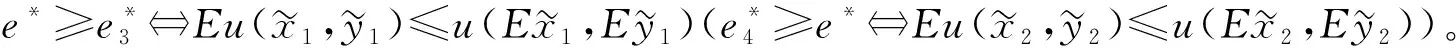
和命题3相比,在命题4中的偏好条件对于保证初始(目标)的两种PQD不确定性在决策者的努力上的正(负)影响是必要和充分的。Li[11]论证PQD是一种比正相关性更强的随机依赖关系。因此,在相同的偏好条件下,对于两种局部风险,正相关性保证更多或更少努力是足够的,但是对于任意的两种风险,必须限定更强的风险依赖结构PQD。
四、努力的货币成本模型
继续考虑转向决策者的努力成本是货币的情形。决策者成本函数表示为c(e),并且c(0)=0,c′(e)≥0和c″(e)≥0。那么,决策者的最大化目标变为:
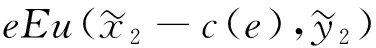
(9)
优化函数(9)的FOC是:
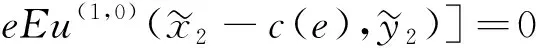
(10)
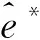
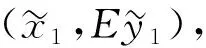
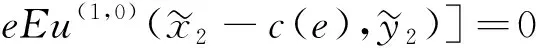
(11)
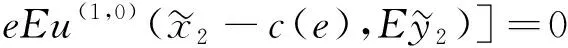
(12)
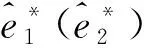
命题5假设努力的成本是货币的。对于独立的两种风险,
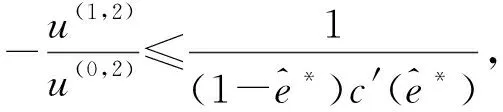
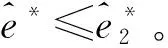
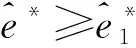
(13)
为了简化,定义一个二维函数:
当u(0,2)≤0和u(1,2)≥0时, 可得出:
(14)
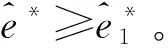
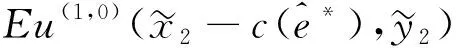
(15)
定义二维效用函数:
有:u(0,2)≤0和u(1,2)≥0⟹g(0,2)(x,y)≤0
(16)
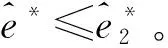
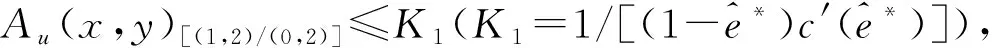
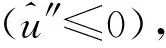
对于两种依赖的局部的风险,获得下列的命题:
命题6假设努力的成本是货币的。
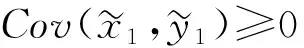
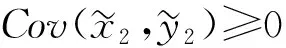
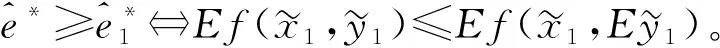
当u(1,1)≤0和u(2,1)≥0, 有
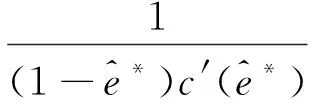
(17)
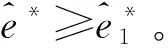
有
u(1,1)≤0和u(2,1)≥0⟹g(1,1)(x,y)≤0 (18)
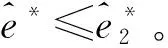
Eeckhoudt等解释u2,1≥0为决策者是背景变量混合谨慎的必要和充分条件,其意味着更高的背景变量取值水平将减轻财富风险的不利影响[13]。Au(x,y)[(2,1)/(1,1)]=-u(2,1)/u(1,1)是背景变量混合谨慎的强度测度。对于初始的两种正相关的局部风险,混合谨慎测度Au(x,y)[(1,2)/(0,2)]≤K1和Au(x,y)[(2,1)/(1,1)]≤K1推出具有在命题6(a)中的偏好的决策者将会做出更多的努力投资。对于最终的两种具有正相关性的局部风险,具有在命题6(b)中的偏好的决策者会做出更少的努力投资。由于风险之间的依赖性,故在命题6中需要更多的风险偏好限定条件。
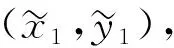
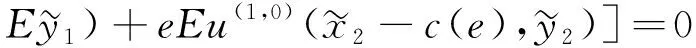
(19)
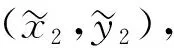
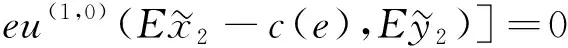
(20)
对于两种相关的局部风险,笔者有如下的命题:
命题7假设努力的成本是货币的。
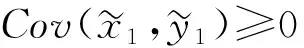
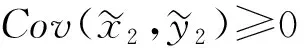
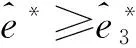
当u(2,0)≤0和u(3,0)≥0, 我们有
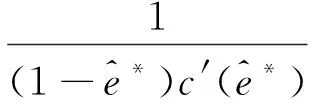
(22)
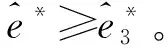
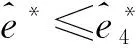
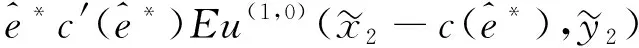
(23)
有u(2,0)≤0和u(3,0)≥0⟹g(2,0)(x,y)≤0
(24)

Au(x,y)[(3,0)/(2,0)]=-u(3,0)/u(2,0)是财富变量谨慎的强度测度。命题7的解释如下。在初始的正相关的两种局部风险下,对于具有在命题7(a)中的风险偏好的决策者,混合谨慎测度Au(x,y)[(1,2)/(0,2)]≤K1和谨慎测度Au(x,y)[(2,1)/(1,1)]≤K1分别直接控制这两种风险在决策者的努力投资决策上正的影响,混合谨慎测度Au(x,y)[(2,1)/(1,1)]≤K1导出这两种不确定的相互影响会重叠加强这些影响。因此,决策者总是做出更大的努力投资。在最终目标的两种正相关局部风险下,u(0,2)≤0,u(2,0)≤0和u(1,1)≤0引起决策者的边际收益减小,然而u(1,2)≥0,u(2,1)≥0和u(3,0)≥0引起他的边际成本增大。因此,决策者将做出更小的努力投资。
继续分析更强的PQD风险对决策者的努力投资行为的影响并得出如下命题:
命题8假设努力的成本是货币的。
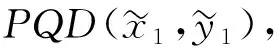
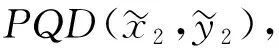
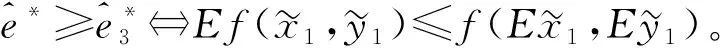
和命题7相比,易知对于两种PQD风险的情况,在命题8中决策者的偏好条件对于保证他的更大(小)的努力投资行为是充分的。
五、结 论
笔者研究在二维效用模型里在财富风险和背景风险下决策者的努力行为决策问题。在存在其他风险时,笔者给出了保证背景变量的不确定性在决策者的努力上正或负的影响的偏好条件。在财富变量和背景变量两种不确定性的同时共存的环境下,笔者讨论当这两种风险是局部的或正象限依赖时,两种变量的不确定对决策者的努力行为的联合效应。笔者给出在相关性背景风险的环境下理性的决策者的最优努力投资行为的混合风险偏好条件。笔者研究在不确定性下影响决策者最优努力投资的不同风险的来源,并且发现两种风险之间的依赖结构在他的努力决策中扮演着重要的角色。笔者的工作将Chuang等[8,14]提出的决策者的努力决策模型扩展到二维风险的框架,研究结果表明,当混合风险加剧或其相关性增大时,风险厌恶的决策者会做出更多的预防性努力投资规避混合风险。笔者对二维不确定性下最优努力决策问题提出一些新的见解,进一步完善了风险厌恶理论的分析内容,在一定程度上解释了传统风险厌恶理论无法解释的一些经济现实、金融行为和现象,为防范化解重大金融风险提供了理论支撑。

