作战试验定性数据处理及样本量估算方法*
薄 云,廖学军,白洪波,白 宇
(1.航天工程大学研究生院,北京 101416;2.中国白城兵器试验中心,吉林 白城 137001;3.航天工程大学航天保障系,北京 102206;4.国防大学联合勤务学院,北京 100039)
0 引言
武器装备的试验鉴定涉及大量指标考核。文献[1]针对如何评价航天领域高科技成果,从技术性、社会性、经济性3 个维度提出了成熟性、可替代性、实用性,劳动生产率贡献度等18 个指标;文献[2-6]针对如何评估多型无人机的作战效能,从攻击、突防、导航、态势感知、完备性、准确性、连续性、时效性、相关性、共享度等维度提出了挂载量、精度系数、发现目标能力、雷达散射截面、信息接受能力等26、7、19、17、25 个指标。可以看出,其考核指标均可划分为两类。一是定量指标,如雷达散射截面、定位时间、精度系数、挂载量等;二是定性指标,如工作可靠度、任务可执行度、成熟性等。定量指标的物理含义明确,基于已有数据可构建概率分布,从而客观考核指标;而定性指标一般用于衡量主观感受,物理含义并不明确,难以直接套用定量指标的考核方法。
作战试验[7-10]作为武器装备试验鉴定研究的热点问题,现已形成一批理论成果,各军兵也已基本完成构建所辖武器装备的作战试验指标体系[11],下一步将加速推进体系中各类指标的考核科学化。考虑到我军在长期的定型试验鉴定实践[12]中积累的大量定量指标考核理论与方法也基本适用于作战试验,但作战试验由于其鲜明的实战化特点,需根据模拟作战任务的完成程度和武器装备对于任务的适应程度来判断武器装备是否达到指标要求[13],因此,作战试验势必存在大量定性指标,而这些定性指标考核基本没有定型试验的经验可供借鉴,故本文首先针对当前作战试验定性指标结论推断存在的问题,提出了基于二分检验的推论框架;其次,鉴于样本量估算对于试验任务经济性、科学性的重要影响,讨论了定性类指标考核的样本量估算方法;最后,演示了该推论框架及样本量估算方法的有效性。
1 作战试验定性指标考核现状
1.1 基本过程
定性变量又称分类变量,它是只能以有限取值或类别加以度量的变量,具体又分为二分变量、名义变量和定序变量[14]。二分变量只有含义完全相反的两个取值;名义变量有有限个取值,彼此没有先后、好坏的差别;定序变量有有限取值,但这些取值含有先后、好坏等差别。
当前,作战试验中的定性指标一般以类似“某型卫星通信系统在典型海事任务中的通话质量满意度大于80%”的方式提出规定要求;以问卷调查的形式采集数据;以定义各种可能结果与特定数值的映射关系(如“非常不满意-1”、“不满意-2”、“基本满意-3”、“满意-4”、“非常满意-5”),使定性的主观感受具备某种定量特征;然后利用加权平均获得指标综合结果,如该结果的数值大于指标规定的数值,则认为该项指标考核通过。
1.2 可改进的方面
由于这些试验的结论是在近似实战条件下由专业作战人员“试用”武器装备后得出的,因此,具备很高的可信度,但经分析仍可得到3 个方面的提高。
1)避免过度设定客观事实。例如:实践中一般以“1”、“2”、“3”、“4”、“5”作为满意度从“非常不满意”到“非常满意”的得分,并用加权平均值作为最终的满意度得分。但是很显然,“非常满意”的满意程度未必是“非常不满意”的满意程度的5 倍,另外,满意程度从“非常不满意”到“不满意”的跨度未必和“满意”到“非常满意”的跨度正好一致,于是其加权平均值也未必客观反映满意度。
2)体现试验的随机本质。很显然,试验是一个随机抽样过程[7],依据样本得出的结果是随机变量,那么很显然,依据样本的加权平均满意度来推断武器装备的满意度是否通过考核必然存在出错概率。更为重要的是,当前依据加权平均值判断指标是否合格的方法并未控制该出错概率。
3)准确估算试验的样本量。以上通过加权值判断指标是否通过考核的方式往往只能依据资源可承受水平来估算样本量,未能充分利用其余的决策支持信息,在样本量估算的科学化水平上还有很大的提升空间。
2 应对策略
2.1 基于比率考核定性指标
作战试验的定性指标大部分是以某种“度”的形式加以提出的,例如满意度、适应度、共享度等。考虑到武器装备的这些定性指标限定为只有“是”、“否”两个选项,那么对于某一作战人员来说,对其回答要么是肯定的,要么是否定的,只是“是”“否”选项的概率不一样。设其回答“是”的概率为p,则回答“否”的比率为1-p。
由于在相近的武器装备水平和军事训练水平下服役的作战人员对于武器装备的优劣具有大体近似的认识水平,所以虽然各作战人员针对某项定性指标回答“是”的概率存在差异,但应该差异不大。因此,可以进一步假设对于拟列装被试武器装备的作战部队来说,其作战人员对于某项定性指标回答“是”的概率都为p。更进一步,如果这些作战部队使用该被试装备,并要求所有作战人员对该定性指标作出评价,那么答案“是”在所有答案中的比率也为p。
可见,以比率的方式定义定性指标具有良好的逻辑自洽性。它很好地规避了以人为设定的多水平定义定性指标可能带来的可信性问题,并且相对后者难以圆满解释加权平均结果的确切含义的情况而言,其结果的实际含义非常明确,对于作战使用和装备管理的指导性也更强。
2.2 以二分检验推断考核结果
为体现试验的随机抽样本质,可参照如下的二分检验[14]过程。假设希望通过作战试验推断被试武器装备的满意度是否大于80%,抽选了n 名参试作战人员,抽样所得数据y→=[y1,y2,…,yn]。其中:

也即在n 名参加作战试验的作战人员中,给出“满意”态度的人数总和s 服从参数为n 与p0的二项分布,记为s~b(n,p0)。其概率分布图形如图1所示。
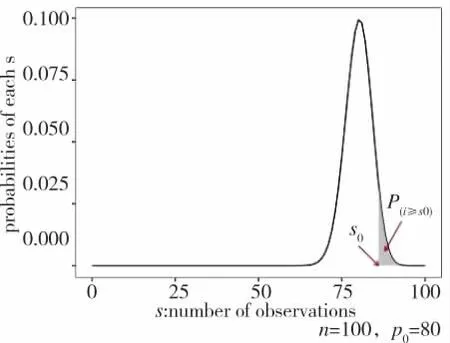
图1 二项分布概率分布示意图
图1 的阴影部分表示了所有s≥s0情况下的发生概率总和。它表达的含义是作战人员总数为n,满意度为p0的情况下,出现样本y→n,以及比y→n更极端情况的概率:
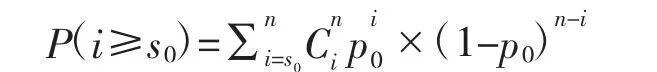
如果P(i≥s0)非常小,则表示得出该概率的前提条件,即满意度为p0(或者更小)的结论非常可疑,应当考虑接受其相反结论,即满意度p>p0。这就是基于二分检验考核定性指标的基本原理。
可以看出,该过程反映了试验的随机本质,更为重要的是它可以明确给出“通过考核”的错误概率(即P(i≥s0))是多少。这种错误在统计学中被称为第1 类错误,其发生概率的可接受水平被称为显著性水平,通常记作α[15]。与之相对的是第2 类错误,它是本应给出“通过考核”但却认为指标不合格的错误,它的发生概率的补数称为统计功效,通常记作(1-β)。其中,β 是第2 类错误的发生概率[15]。它们的关系如图2 所示。
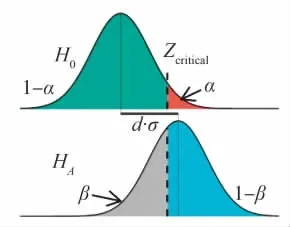
图2 原假设、备择假设、显著性水平与统计功效的示意图
2.3 依据客观准则估算样本量
2.3.1 估算的客观准则
影响试验样本量的因素很多,比如资金消耗、日程安排、资源的可配置情况、以及试验结论的可靠性等等,但最根本的影响因素还是试验结论的可靠性。如前所述,显著性水平α、统计功效(1-β)是控制两类错误的重要工具。但实际工作中,常常忽略统计功效,甚至很多顶级刊物也无法避免[16-19]。如图3 所示,对某一个特定的研究问题而言,所有正确的备择假设占所有假设的比例分别为50 %和10 %时,通过假设检验找出正确结论的比例ppv(positive predictive value),会随着统计功效的降低而迅速降低。
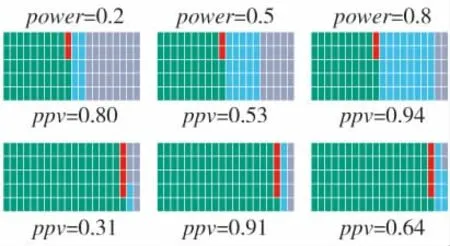
图3 ppv 随(1-β)变化的示意图
在图3 中,如果指标实际并未达标,其被正确识别的比例proppm用绿色色块表示,被错误识别(即第1 类错误)的比例propnn用红色色块来表示;如果指标确实达标,其被正确识别的比例proppa用蓝色色块表示,被错误识别(即第2 类错误)的比例propna用灰色色块表示。设真正达标的武器装备的比例为:
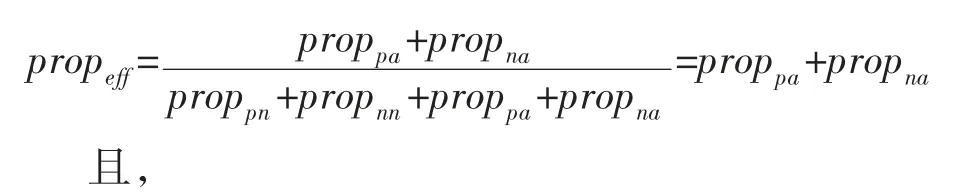
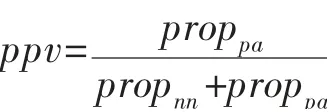
可以看出,当propeff=0.5 时(上3 幅分图的情况),若(1-β)分别为0.2、0.5 和0.8,ppv 则分别为0.80、0.91 和0.94;当propeff=0.1 时(下3 幅分图的情况),若(1-β)分别为0.2、0.5 和0.8 时,ppv 则分别为0.31、0.53 和0.64。即得出真正正确结论的比例,会随着统计功效的降低而迅速降低。由于武器装备是否具备宣称的创新成效直接关系到作战人员的生命安危和战争的胜败,而图3 中,当propeff=0.1,(1-β)=0.2 时,ppv 仅为0.31,即在10 型通过作战试验的武器装备中,大约只有3 型才真正具备宣称的作战效能和作战适用性。这种结果显然是灾难性的。因此,在作战试验中,在确定显著性水平以控制第1 类错误的基础上,必须确保统计功效以控制第2 类错误。
2.3.2 估算的方法步骤
基于以上讨论,作战试验依据二分检验考核定性指标的样本量估算可按如下流程实施。
第1 步,由武器装备的研制总要求得出定性指标的具体要求,构建假设检验;
第2 步,根据武器装备的研制试验或前期其他试验,估计武器装备该指标的实际水平;
第3 步,确定试验期望达到的显著性水平α 和统计功效(1-β);
第4 步,设样本量n 为1;
第5 步,计算在前述设定的p0、pa、α 情况下的临时统计功效(1-β)temp,并计算(1-β)temp和期望达到的(1-β)差值的绝对值Δ(1-β);
第6 步,令n=n+1,重复第5 步,直至Δ(1-β)最小。此时的n 即为满足以上条件的样本量。
3 算例演示
3.1 样本量估算的过程演示
假设研制总要求规定某型卫星通信终端通话质量的满意度大于80%,则计算过程如下:
第1 步:定义p 为满意度水平,构建假设检验H0:p≤p0=0.80,Ha:p≥p0=0.80;
第2 步:通过考察该型卫星通信终端的研制试验、早期作战评估、作战评估的相关数据,估计pa的实际水平大约为0.91;
第3 步:设定假设检验的显著性水平α=0.05,期望达到的统计功效(1-β)=0.80;
第4 步:设定试验所需的样本量n=1;
迭代第5 步与第6 步的运算:由已设定的α=0.05、期望达到的(1-β)=0.80、估计的pa=0.91,从n=1 开始,以1 为步长递增n,计算在n 取各值情况下的Δ(1-β)。迭代运算结果如图4 所示。通过比较,取使Δ(1-β)达到最小数值0.002 7 的n 值,即72,作为待求的样本量。在此样本量n 条件下H0、Ha、α、(1-β)的关系如图5 所示。

图4 迭代求取满足α 和(1-β)的样本量n 的过程示意图
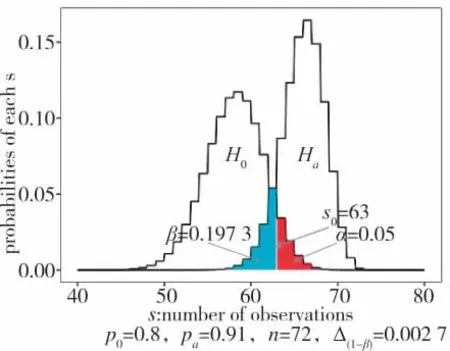
图5 在已求取样本量n 情况下的二分检验示意图
3.2 考核定性指标的有效性演示
首先设定仿真参数为n= 72、α=0.05、p0=0.80、pa=0.91;
其次以50 为步长,设定仿真次数tsim为50 至10 000;
接着在tsim的每次仿真中生成100 组长度为n=72、满意度pa=0.91 的(“满意”、“不满意”)二分随机向量y→sim,计算y→sim中结果为“满意”的总数ssim,并计算在以n=72、p0=0.80 为参数的二项分布中出现比ssim及比ssim更极端的发生概率psim,如果psim<α,则表示模拟的样本数据y→sim支持Ha;记该组100 个y→sim支持的Ha总数为ty(a),ty(a)/100 即为tsim的每次仿真中算得的经验统计功效(1-β)exp(y);当tsim次仿真均做完之后,以tsim个(1-β)exp(y)的平均数(1-β)exp作为与tsim相对应的经验统计功效;
最后,当完成所有按照tsim所做的仿真之后,统计与tsim相对应的(1-β)exp,形成如图6 所示的最终结果。
通过观察图6 可以看出,经验统计功效(1-β)exp大致以0.803 为中心,在(0.796,0.808)的范围内上下波动,并随着tsim的增大而迅速收敛值0.803。由此可证明,本文给出的基于二分检验考核定性数据及其样本量的估算方法可有效满足作战试验控制两类错误风险的客观需求。
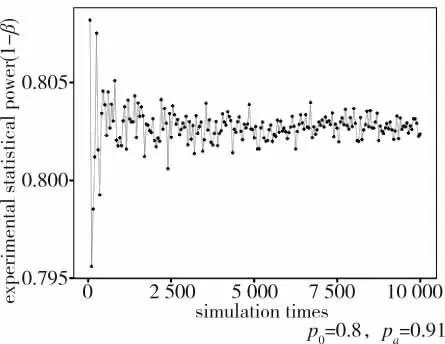
图6 算法有效性验证示意图
4 关于方法应用的讨论
4.1 Δ(1-β)可能存在多个最小值的处理
通过图4 可以看出,在求取满足α 和(1-β)需求的样本量n 的过程中,Δ(1-β)在下降至最小值再增大的过程波动非常剧烈,而不是一个平滑变化的过程。这主要是由于定性数据的精确检验方法,无论是原假设,还是被择假设,其分布率均为离散函数,所以在求取样本量的过程中计算Δ(1-β)可能会产生如图4 所示的震荡过程。为了应对这一情况,建议在实践中如果出现多个备选样本量n 使得Δ(1-β)达到最低点的情况,选择这几个备选n 中选择处于中间位置的n。
4.2 验前信息对于样本量估算的影响
图7 给出了通过以上方法求取的样本量n 的变化趋势。其中,实线趋势曲线为p0=0.7,pa取各值情况下样本量n 的变化趋势;虚线趋势曲线为pa=0.7,p0取各值情况下样本量n 的变化趋势。可以看出,无论固定了p0或pa的任何一方,在另一方作为变量的情况下,g=pa-p0越大,则所需的样本量越小。g 在统计学中被称作效应量[20],它反映了备择假设的显著性程度。
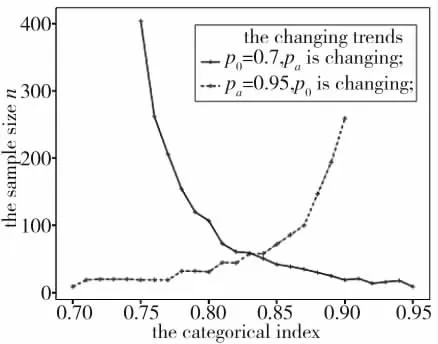
图7 样本量n 变动趋势示意图
由于作战试验前无法知道g 的真实值,只能利用研制试验、早期作战评估、作战评估的相关数据,或者在验前先小规模组织相关测试,采集相关数据,从而对g 进行估计。g 估计得越准确,则样本量估算得越准确,相应试验资源的综合效益也越高。
4.3 更复杂数据的处理
本文提出的方法对于作战试验中定性数据处理及其样本量估算的大部分情形来说是足够适用的。虽然这些方法是针对单个试验样本考察其是否达到研制总要求规定的特定指标,但是稍加变形,也可以处理被试武器装备相对于基线作战力量的定性数据处理。
另外,针对一些特殊的定性数据,需要使用一些特殊的数据处理方法,例如定序数据的相关处理方法。这些问题的假设检验过程还比较直观,但其概率分布函数或分布律非常复杂,难以精确估算样本量,必要时需要使用蒙特卡洛仿真求解。
5 结论
通过分析当前作战试验的指标考核现状,本文指出它可以在避免过度设定事实、反映试验的随机本质和样本量计算3 个方面得到科学化水平的提升。以定性指标考核为例,本文研究了引入二分检验和基于统计功效的样本量估算来实现提升的途径。通过某型卫星通信终端通话质量满意度考核的具体算例,本文演示了该途径实现以上3 方面提升的实际效果。最后,针对该实现途径在实际考核中可能会出现的一些特殊情形,本文讨论了相应的处置办法,从而为后续作战试验的相关实践提供了有益参考。

