基于机动识别的多级组合滤波器设计

徐 磊，刘晓阳，郑 晟，徐金龙，王中晔

（上海机电工程研究所，上海 201109）

0 引言

信号在传输和检测过程中不可避免地受到系统内部和外界环境噪声的干扰，严重影响了信号的质量［1］。对于含有噪声的信号，首先要滤除噪声，然后提取出所需信号，这个过程就是滤波。滤波问题，尤其是机动目标的滤波，是目标跟踪过程的重要组成部分，已经在航空航天、测量等军用和民用领域得到了广泛应用。目前，工程上常用的滤波方法有卡尔曼滤波［2-3］、α-β 滤波、α-β-γ 滤波［4-7］，以及平方中心差分卡尔曼滤波（SRCSKF）［8］等。

滤波是一种线性最小方差估计，对于每一点采样值的估计，都要求估计误差方差矩阵最小的最优估计方法，然而，这种最优估计方法需要大量的在线计算量。通过简化滤波器增益的选取，使之不再与系统协方差相关，从而实现增益的离线计算和滤波器的工程实现。α-β-γ 滤波正是基于这样的需求而建立的常增益滤波器。

固定增益α-β 滤波器的在线计算量最少，能够有效保证滤波算法的实时性。然而，在滤波暂态阶段，滤波算法尚未收敛，小增益滤波器的滤波性能将很差。同样，在目标机动时，目标观测值与滤波预测值之差（新息）较大，为了保证较好的滤波效果，必须增大观测值在滤波方程中的比重，对于α-β 滤波，一个可行的方法就是增大滤波器的增益α、β。然而，作为一种常增益滤波算法，因为增益固定，α-β滤波很难在实现对机动目标暂态跟踪的同时还满足较好的稳态滤波性能。

为了兼顾机动目标的跟踪性能和稳态滤波的精度要求［7-9］，本文在现有工作基础上，提出了基于机动识别的多级组合滤波方案。该滤波算法首先通过对目标的运动特性，尤其是机动特性进行了量化处理；然后，通过仿真和调试，根据目标的机动程度，设计不同增益的α-β 滤波器，并确保每个滤波器对相应运动特性目标的滤波是最优的；最后，建立有效的机动检测机制和野值剔除准则，实现多个滤波器之间的有效切换，使得设计的组合滤波器能够有效解决暂态跟踪和稳态滤波精度之间的矛盾。

1 α-β 滤波器

2 机动识别组合滤波器设计

不失一般性，本文仅考虑运动目标的位置和速度估计问题。在设计组合滤波器之前，首先，根据任务需求（如滤波器收敛速度、滤波精度指标等），通过大量仿真，分别构造了适应不同滤波任务的多个最优α-β 滤波器。然后，通过对滤波输入数据进行野值判别，若数据异常，则直接剔除，并通过滤波外推；若数据正常，进入机动识别。最后，通过机动检测对目标的运动特性进行判别，并根据判别结果自动切换至最优滤波器，以达到最优的滤波效果。

2.1 滤波器工作原理

为了得到多级组合滤波器设计的一般性结论，本文以N 级组合滤波器为研究对象。

假设通过需求分析，本文设计了N 级α-β 滤波器F1，F2，…，FN且滤波器精度P 满足P1＜P2＜…＜PN，滤波原理图如下页图1 所示：

图1 组合滤波器工作逻辑流程图

具体处理过程如下：

测量数据首先进入野值判别模块，通过建立的野值判别机制对测量数据进行检测。如果数据异常，则剔除当前测量值；然后，启动滤波重启判别模块，用于判别连续剔点数是否超过设定的阈值，如果连续剔点数大于M 点，则整个滤波器重启；否则，启动机动检测与滤波切换模块中的滤波器Fi（i∈［1 N］）进行外推处理，其中，Fi表示上一时刻测量数据所采用的最优滤波器。

测量数据经野值判别模块判断为正常数据后，进入滤波收敛判别模块。通过对滤波器滤波点数的统计，滤波收敛判别模块确定滤波器是否进入稳态；若当前仍然处于滤波的暂态阶段，为了让滤波器尽快收敛，选择具有更快收敛速度的滤波器F1；若组合滤波器已经收敛，则启动机动检测与滤波切换模块，根据目标的机动程度选择对应的最优滤波器：目标机动大，则选择收敛速度快的滤波器，确保对机动目标的跟踪；目标机动小，则选取精度高的滤波器，保证滤波精度。

2.2 野值剔除与机动识别

2.2.1 野值剔除

算法具体构造如下：基于k-1 时刻的位置、速度滤波值，使用如下线性外推方程（笛卡尔坐标系下的线性外推与文中假设目标等速直线运动的前提是一致的）

2.2.2 机动识别

本文通过对残差的分析，建立了机动的多点识别机制，提出了一种更为简单且准确的机动判别算法。该方法包括两个步骤：第一，使用滤波预测值和剔点后采样值比较，给出初步判别结果；第二步，建立多点判别机制，通过连续多点判别的结果，确定最终的机动判别结果。

为了保证滤波器切换的可靠性，避免频繁切换和误切换所带来的问题，本文充分考虑目标的惯性特性，建立了目标机动判别的“多点判别”机制（本文规定机动判别是建立在滤波器已经收敛的基础上），即结合k、k-1、k-2、…、k-n 时刻的机动判别结果，最终确定当前k 时刻目标是否机动。下面以X轴方向的滤波为例，基于目标在X 方向k 时刻3 点机动识别流程图（图2）为例，阐述“多点判别”机制的原理。

图2 K 时刻目标在x 方向的“3 点机动判别”原理

1）当前点机动初步判别

在X 方向设定残差阈值ΔXmax，当目标在k 时刻的位置，采样值X（k）与k 时刻的滤波位置预测值X^（k，k-1）之差大于该方向阈值时，则认定X 方向当前时刻为机动，即，

成立，则目标在X 方向k 时刻为机动。

2）多点机动判别

①如果目标在X 方向k 时刻机动，则进一步判断k-1 时刻目标是否机动，如果机动，则判定目标在k 时刻机动；否则，进一步判断k-2 时刻目标是否机动，如果机动，则判定目标在k 时刻机动，否则，目标在k 时刻为不机动。

②如果目标在X 方向k 时刻不机动，则进一步判断k-1 时刻目标是否机动，如果不机动，则判定目标在时刻不机动；否则，进一步判断k-2 时刻目标是否机动，如果k-2 时刻目标机动，则判定目标在k 时刻机动，否则，目标在k 时刻为不机动。

2.2.3 启动判据

至此，本文已经建立了野值判别和机动识别机制，但是对于野值和目标机动同时存在的情况，如果不能有效区分当前采样值是野值还是机动数据，那么，这两种判别算法会相互影响，从而不可避免地影响滤波效果，甚至造成滤波发散。

针对暂时无法辨别是野值或机动的“不确定”测量数据，文献［10-11］这两种方法对“不确定”采样数据的判别都有一定的效果，但是前者未考虑判别结果的时间滞后性，且该方法未明确给出滤波点数的积累时间，而后者则建立在野值数据不可能连续出现的前提下。

本文提出的多点机动判别机制通过对多个采样点的连续判别，最大程度保证了机动判别结果的可靠性。因此，如果先进行可靠性高的机动判别，那么，对“不确定”采样数据的判别将会简化很多。因为对“不确定”采样数据的判别，如果首先进行野值剔除，会增大“不确定”点误判的概率和判别复杂性。由此，建立了机动识别与野值剔除启动判据，具体流程如图3 所示。

图3 机动判别与野值剔除启动判据

机动判别与野值剔除启动判据如下：对测量数据进行机动判别，如果目标不机动，则紧接着进入野值判别，如果判定采样数据为野值，则启动野值滤剔除波器；对于既不是机动又不是野值的数据，进行正常数据滤波。如果目标判别为机动，本节增加了一个机动范围判别模块，如果目标当前时刻的位置超出目标可能的最大机动范围，则判定当前采样值为野值，否则进行机动目标滤波。

仍然以X 方向的判别为例，对该模块功能作简单论述。设目标在X 方向机动所能达到的最大加速度为amax，那么，在k 时刻，目标在X 方向所能达到的最大运动范围为：

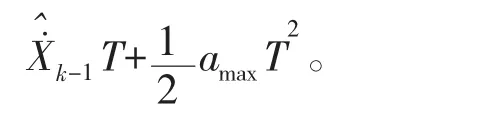
如果目标在某一时刻的运动范围超出其最大机动加速度所能达到的边界值，那么可以判定该测量值野值，否则，启动机动目标滤波。机动范围判别模块的引入进一步增加了野值判别裕度，确保了野值数据不被当做机动处理，从而最大程度地避免了野值的误判。

2.2.4 组合滤波器切换

以X 方向机动量化和滤波切换为例，阐述组合滤波器的切换原理。

在滤波初始和目标机动阶段，可以设置较低的机动判别门限和机动程度量化门限，尽量调用高增益滤波器，可以有效抑制滤波暂态误差；减小机动判别门限虽然可以降低机动漏判的概率，但是过低的门限会使非机动阶段的滤波误差增大，因此，机动门限一般以覆盖目标非机动阶段滤波的最大稳态误差为准。另外，当滤波精度和跟踪性能不能兼顾时，应该以滤波算法的稳定性为前提，即尽量选用机动目标的滤波器，因为机动目标滤波器处理非机动目标，不会引起滤波的发散。

3 仿真验证

本节以某一典型大机动运动目标为对象，该运动目标的运动特性如下：0 s～73 s 做平飞运动，73 s～120 s 机动，且机动在X 方向进行。本文在球面坐标系的斜距R 和方位角A 两个自由度上进行机动判别。斜距R 和方位角A 的机动判别门限如表1所示。

表1 机动判别门限

3.1 组合滤波算法XYZ 方向滤波

图4～图6 分别给出了最优组合滤波算法在X，Y，Z 轴方向的滤波结果。从这3 张图可以看出，目标在Y，Z 轴方向可近似为匀速运动，在这两个方向，本文的滤波算法均给出了较为平滑准确的跟踪性能。在X 方向，k=73 s 之前，目标也是匀速运动；73s 之后，目标开始机动。对于匀速阶段和机动阶段的滤波，组合滤波算法均给出了较好的跟踪性能和精度。

图4 X 方向滤波

图5 Y 方向滤波

图6 Z 方向滤波

3.2 组合滤波算法与单独α-β 滤波算法的比较

因为目标机动主要在X 方向，不失一般性，本节的比较主要在该方向进行。图7 给出了组合滤波算法与两种不同增益的α-β 滤波算法在X 轴方向滤波误差曲线。

图7 不同滤波器X 轴方向跟踪误差比较

从图中可以看出，在k=73 s 之前，目标做平飞运动，组合滤波器的滤波误差比其他3 个滤波器都小。在k=90 s 之后，滤波器1 和滤波器2 的滤波误差均出现了增大现象，而滤波器3 与组合滤波器则完全重合了。这说明滤波器检测到目标强机动后，组合滤波器切换至滤波器3 进行强机动滤波。因此，本文提出的组合滤波器，不管目标是匀速运动还是机动，在机动跟踪和稳态精度上都表现出了较好的性能。

值得注意的是，图7 所示的滤波器3 表现出和组合滤波器类似的性能，这可能是滤波器参数设置造成的。但这也同样说明，对于不同运动特性的目标，提高滤波器增益，可以保证滤波算法的收敛特性。

3.3 野值剔除与机动判别的准确性

从工程角度出发，我们不希望滤波算法将机动误判为野值，因为连续剔除野值对滤波算法的精度，甚至稳定性都带来影响。为了更有针对性地验证机动判别与野值剔除的正确率，本文针对目标机动阶段的野值剔除进行了如下处理：选取目标机动阶段的连续6 个时刻，设置k=100 s 和k=101 s 的数据为野值后，通过仿真，我们得到如表2 所示结果。

从表2 可以看出，本文建立的机动判别和野值剔除方法，能够精确剔除目标机动阶段的野值，同时不影响相邻时刻目标机动的判断。

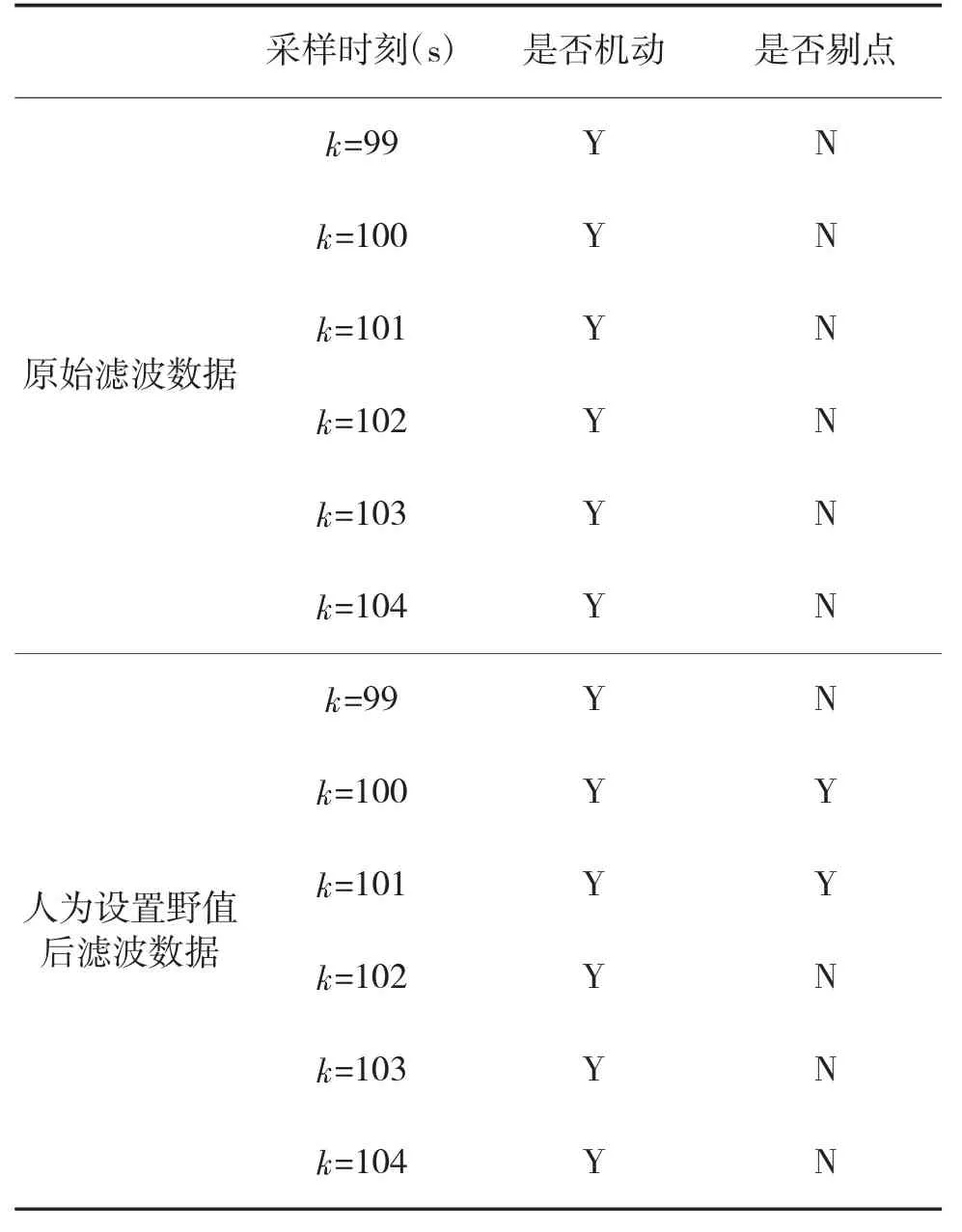
表2 机动判别与野值剔除

4 结论

本文从工程可实现的角度出发，针对机动目标滤波问题展开了讨论，提出了基于机动识别的组合滤波算法。建立了较为准确的多点机动识别机制，并对机动过程的野值剔除方法也作了进一步讨论。本文通过仿真充分验证了野值剔除与机动判别的准确性，且与单独滤波算法相比，组合滤波算法表现出了更优的性能。