基于D-D中子源校准中子周围剂量当量仪的最小房间尺寸研究

田兴宇，张雄杰，汤 彬,胡 斌，宋乐天

(1.核技术应用教育部工程中心，江西 南昌 330013；2.东华理工大学，江西 南昌 330013)

1 引 言

中子周围剂量当量仪是用于各种场所或环境下中子辐射水平监测的设备。为确保仪器处于良好的技术状态，保证测量结果的准确性，需要定期对仪表进行校准[1,2]。目前，国内外的中子周围剂量当量仪的校准规程中依然主要使用同位素中子源对仪表进行校准[3～6]。相比于同位素中子源，D-D中子源有着便于携带、在非运行过程中并不会产生很强的放射性等诸多优点[7]。所以，加速器中子源是一种非常适用于中子周围剂量当量仪校准的中子源，其拥有良好的安全性与环境适应能力。由于散射中子会对中子周围剂量当量仪的校准产生影响，所以在中子周围剂量当量仪校准过程中，需对散射中子本底进行扣除[8～11]。在仪器校准的过程中，入射的散射中子主要由实验室墙体产生，其在总计数中所占比例受房间内部空间尺寸影响。为推动D-D中子源在中子周围剂量当量仪校准过程中的应用，本文对在不同房间尺寸下D-D中子源所产生的散射中子进行了模拟计算，并对计算结果进行了分析。

2 散射中子本底扣除

中子周围剂量当量仪是测量中子辐射水平的装置。通常情况下，在一个中子辐射场之中，对测量仪器的读数产生贡献的除了源中子之外，还包括经过空气、实验室墙体、地面、天花板等散射进入测量仪器的散射中子[8,12,13]。在中子周围剂量当量仪检定过程中，通过校准获得的被校中子周围剂量当量仪的校准因子或响应是仪器的固有特性，其结果与中子周围剂量当量率、中子谱或中子入射角度有关，而与校准装置及校准方法无关。根据文献[3]中所给出的被校仪器校准因子计算方法，校准因子N为约定真值与扣除散射中子后得到的直接中子束引起的仪器读数的比值。约定真值的计算中，需要考虑散射修正因子，所以散射中子的修正会影响被校仪器校准因子的计算，从而影响仪器校准。因此需要对散射中子的影响进行修正。

2.1 散射中子本底扣除方法

根据国际标准，散射中子本底扣除方法被分为距离变化法以及影锥法等两种。其中距离变化法是基于距离平方反比律的散射中子本底扣除方法；而影锥法，则是利用影锥锥体对中子源所直接射出的源中子进行屏蔽，之后根据仪器的读数直接得出散射中子对剂量当量率的贡献的方法。当散射中子对测量结果的贡献小于直射中子和散射中子对测量结果共同贡献的40%时，可以使用影锥法对散射中子进行直接计算，影锥对直接入射的源中子的屏蔽过程如图1所示。

图1 影锥法屏蔽过程Fig.1 Shielding process of shadow cone method

相对于距离平方反比律的散射中子本底扣除方法，影锥法可以适用于多种不同的测量环境，并且能够更为准确地测量出散射中子的贡献。根据统计，使用影锥法所得的散射修正结果的不确定度约为2%，而距离平方反比律扣除法所得结果的不确定度约为10%[8]。

根据国际标准所推荐的结构尺寸[1,4]，影锥通常由20 cm长的铁制前端椎体与30 cm长的含硼石蜡(含硼率大于5%)后端椎体组合而成。使用影锥法的最小校准距离需大于影锥结构长度的两倍，使用该方法进行散射中子本底扣除需要针对探测器定制专门的影锥椎体，实验成本相对较高。为此，本文提出能量截断法，用于使用D-D中子源进行中子周围剂量当量仪校准时的散射中子本底扣除。

2.2 能量截断法

能量截断法是蒙特卡罗方法计算散射中子的一种特有方法，其通过设置截断阈，对能量低于和高于阈值的数据进行单独处理从而完成散射中子的测量。在测量过程中，入射探测器的中子分为2种，1种是直接入射中子，1种是散射入射中子。直接入射中子是指由中子源发出，在入射探测器的过程中未与其它物质发生相互作用的中子；这类中子的特征为其所带能量在入射过程中未发生改变。散射入射中子是指在运动过程中与墙体、地面、天花板以及空气中的物质发生相互作用从而改变运动方向入射探测器的中子；这类中子的特征在于与物质发生过相互作用，其所带能量有一定的损失，会低于直接入射中子所带能量。所以，根据散射入射中子这一特性，可将直接入射中子所带能量设为截断阈值，只对能量低于截断阈值的中子进行测量，从而完成对散射中子的测量，截断阈可根据实际情况进行调整。

使用这种方法进行散射中子的测量需要保证中子源所放出的源中子能散度极小，所以并不适用于传统同位素中子源。但D-D中子源所发出的源中子所带能量具有良好的单色性，能够满足能量截断法的使用条件。在使用D-D中子源进行中子周围剂量当量仪校准时，只需对入射探测器的中子设置截断阈，只对低于D-D中子源所发射中子能量的中子进行测量。这种测量方法与影锥法原理相同，都是在屏蔽直接入射中子的基础上对散射中子进行测量计算的方法。相比于影锥法，能量截断法的优点在于不需要专门为测量准备相应尺寸的影锥结构；缺点在于只能应用于产生源中子所带能量单色性较好的中子源，具有一定的局限性。使用能量截断法计算散射中子所占比例的公式如式(1)所示。

(1)

式中：S表示散射中子对仪器读数贡献所占百分比；Es表示所带能量低于源中子的中子入射概率之和；Ez表示能量等于源中子的中子入射概率之和。

由于能量截断法并不是中子周围剂量当量仪校准过程中所给出的散射中子本底扣除方法，所以需对其准确性进行验证。本文使用MCNP5软件对2种方法进行了模拟验证。

2.3 能量截断法的验证

构建一个内部空间为L=W=H=500 cm的立方体房间，将中子源与探测器放置在与房间中心点水平位置处，中子源距离房间中心点37.5 cm，中子源与探测器之间距离为125 cm。探测器根据国际标准ISO 8529-2[4]，使用半径为10 cm的球形探测器，影锥椎体后端与探测器距离50 cm，影锥前端与中子源距离25 cm，使得影锥结构正好可将从中子源直接入射探测器的中子屏蔽掉。中子源设置成放出中子能量为2.8 MeV的D-D中子源[3]，影锥、中子源、探测器在房间的具体摆放位置如图2所示。

图2 影锥、中子源、及探测器摆放示意图Fig.2 Layout of shadow cone,neutron source and detector

在使用影椎法完成测量之后，将影椎结构去除，中子源以及探测器摆放位置不变，使用能量截断法再一次进行测量。由于在模拟过程中使用的是D-D中子源，其所产生的中子能量可认为是单色的；但考虑到现实中D-D中子源所产生中子具有一定的能散度，在使用能量截断法进行计算的过程中可适当降低截断阈的阈值。在完成模拟计算后，截取所有入射探测器的中子中能量低于2.7 MeV的中子，这一部分中子即为通过能量截断法所得的散射中子；之后将通过能量截断法所得的散射中子计算结果与之前影锥法所得出的散射中子测量结果进行对比，从而判断2种方法所得结果是否一致。

为了测量不同情况下的散射中子，本文改变了房间墙体的厚度，进行了多次测量对比，其对比结果如表1所示。通过表1可以看出，4组能量截断法所得散射中子入射概率与影锥法所得散射中子入射概率对比结果的相对误差均小于1%，所以可以判断能量截断法求得的结果是准确的。

表1 能量截断法所得散射中子与影锥法所得散射中子结果对比Tab.1 Comparison of scattering neutron results obtained by energy truncation method and shadow cone method

2.4 模拟结果可靠性验证

由于之前所得结果均由模拟计算所得，为确保模拟结果的可靠性，需要对其进行验证。参考国标JJG852[3]中所给出的散射本底占40%时的最小实验室尺寸数据，当使用Am-Be中子源时，散射本底占40%的正方体房间尺寸为L=W=H=300 cm，长方体房间尺寸为L=W=2H=430 cm，中子源与探测器之间的距离为75 cm。

根据以上数据，使用MCNP5软件分别对2种房间进行构建，中子源设置在房间中心点，探测器设置为直径20 cm的球形探测器，其球心设置在经过房间中心点的侧面墙面的垂线上，中子源中心点与探测器球心之间距离75 cm。考虑到JJG852中所用中子源为Am-Be中子源，在模拟过程中需将中子源设置为半径5 cm的球形体源，体源重心设置在房间中心点处[14]，体源各个点所发射的中子能谱如图3所示。

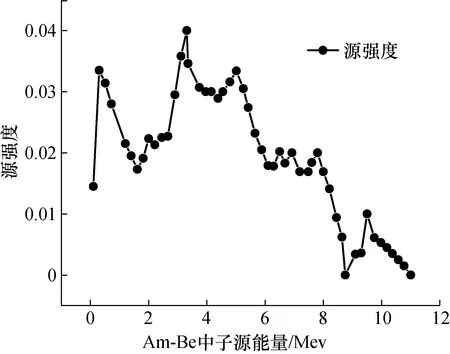
图3 体源各点所发射中子能谱Fig.3 Spectrum of neutrons emitted from each point of the volume source

在房间与中子源构建完成后，通过影椎法得出了2种房间中散射中子对仪器读数贡献占比，其结果如表2所示。

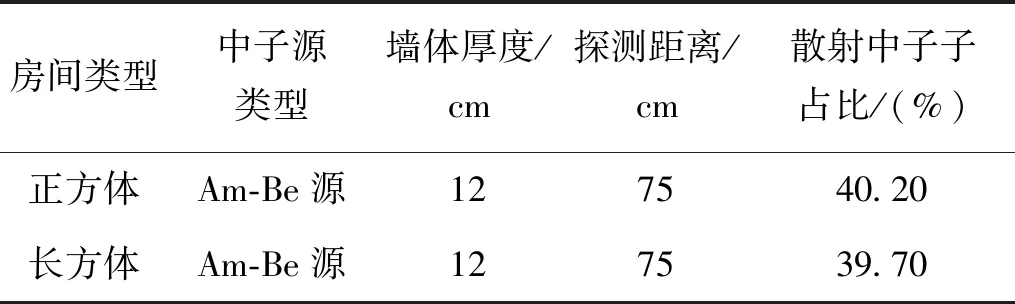
表2 2种房间中散射中子对仪器读数贡献占比Tab.2 Contribution ratio of scattered neutrons to instrument readings in two kinds of rooms

根据表2可知，MCNP模拟所得的散射中子对仪器读数贡献占比与JJG 852[3]中所给的40%这一参考数据基本吻合，由此判断通过MCNP模拟所得结果是可靠的。

3 不同尺寸房间的中子散射比

在测量过程中，对仪器产生贡献的散射中子主要来自于实验室墙体、天花板以及地面的散射。所以，房间内部空间尺寸以及探测器的摆放位置是影响散射中子对仪器读数贡献的主要因素。

3.1 探测器的摆放位置

为确定最为合适的探测器摆放位置，本文基于MCNP5构建了一内部空间尺寸为L=W=H=300 cm 立方体房间。中子源的摆放位置参考国际标准ISO 8529[4～6]放置于立方体房间中心点；探测器设置为直径20 cm的球形探测器，其球心设置在经过房间中心点的侧面墙面的垂线上。中子源为产生中子能量2.8 MeV的D-D中子源[3]，考虑到实际中D-D中子源的能散度，在使用能量截断法时将截断阈设置为2.7 MeV。为判断探测器与中子源之间探测距离对散射的影响，本文对不同探测距离下散射中子对仪器读数贡献所占百分比进行了模拟计算，计算结果如表3所示。

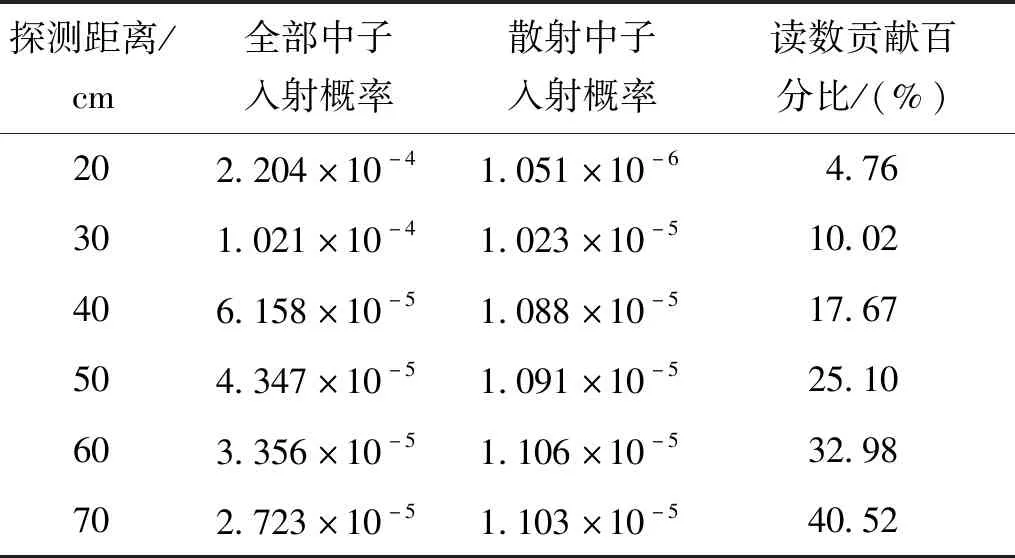
表3 不同探测距离下散射中子对仪器读数的贡献Tab.3 Contribution of scattered neutrons to instrument readings at different detection distances

通过表3可知，随着探测距离的增加，散射中子对仪器读数产生贡献在全部入射中子产生贡献中所占的百分比也会增加。为此，在测量过程中，理应在考虑探测器体积影响的情况下，尽可能的选用小的探测距离。考虑到探测器体积会对测量结果产生影响，本文基于之前的探测器摆放方式，将探测器更改为点探测器，对不同探测距离下点探测器与球形探测器的测量结果进行模拟计算，并根据计算结果得出了2种探测器所得结果的比值F，计算方法如式(2)所示。

(2)

式中：φ1为球形探测器的粒子入射注量率；φ2为点探测器的粒子入射注量率。

2种探测器计算所得结果对比如表4所示。

表4 2种探测器所得结果对比数据Tab.4 Comparison data of two kinds of detectors

根据表4可知，当探测距离大于75 cm时，2种探测器所得结果的比值F趋近于1，即当探测距离大于等于75 cm时，可忽略探测器体积所产生的影响。所以，为保证散射中子对仪器读数贡献最小化，中子源应设置在房间中心点，探测器球心应设置在经过房间中心点的侧面墙面的垂线上，且探测器球心与中子源之间距离应设置为75 cm。

3.2 不同尺寸房间中的中子散射比

基于之前所得的探测器摆放位置，本文构建了不同的类型的房间[3]，并使用MCNP5及能量截断法对这些房间中的中子散射情况进行了模拟计算。房间类型分为2种，分别是内部空间为正方体，墙体厚度为12 cm的正方体房间(内部空间L=W=H)；内部空间为长方体，墙体厚度为12 cm的长方体房间(内部空间L=W=2H)。中子源设置为产生中子能量为2.8 MeV的D-D中子源[3]，考虑到实际中D-D中子源的能散度，在使用能量截断法时将截断阈设置为2.7 MeV。探测器使用文献[4]所给出的直径为20 cm的球形探测器[4]。

在确认所需计算的房间类型之后，对不同尺寸房间的散射中子进行计算，并根据不同类型房间的散射比随房间尺寸的变化情况做出变化曲线。

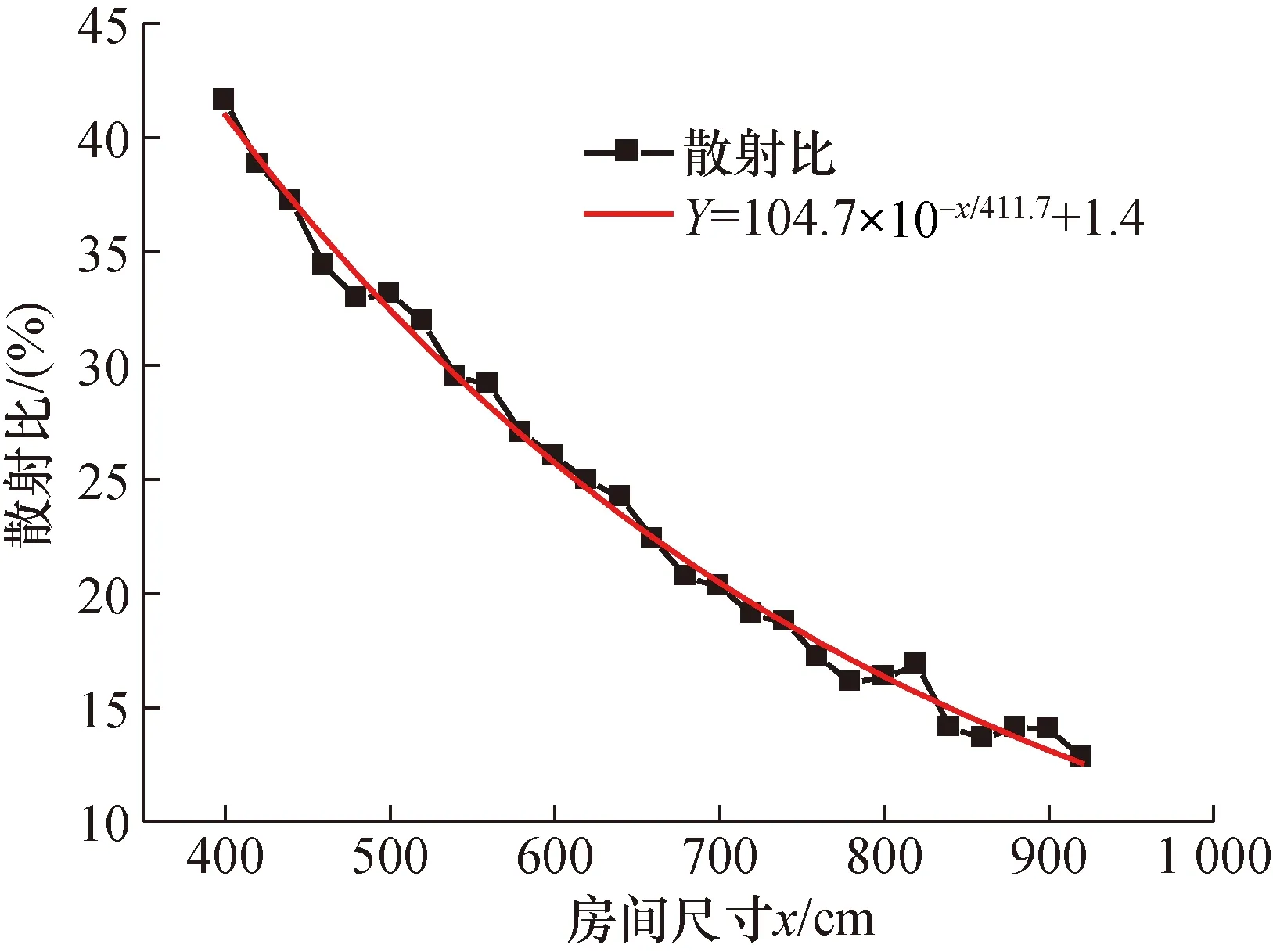
图4 正方体房间散射比变化曲线Fig.4 Variation curve of room scattering ratio of cube

图4、图5给出了2种房间中散射比的计算数据及其拟合曲线(图4中x=L=W=H，图5中x=L=W=2H)，可以看出随着房间内部空间尺寸的增加，散射中子所占比值会逐渐减小，整个衰减过程符合指数衰减规律。由于散射中子对仪器读数贡献占比大于40%时，无法对散射中子进行直接测量，而根据距离反比平方法进行散射本地扣除的不确定度较大，会影响仪器的校准；所以在使用D-D中子源进行中子周围剂量当量仪校准需保证散射中子对仪器读数产生的贡献在直射中子和散射中子产生的总贡献中所占比例低于40%。散射中子对仪器读数贡献占比为40%时的房间尺寸，即是使用D-D中子源进行中子周围剂量当量仪校准所需的最小房间尺寸。

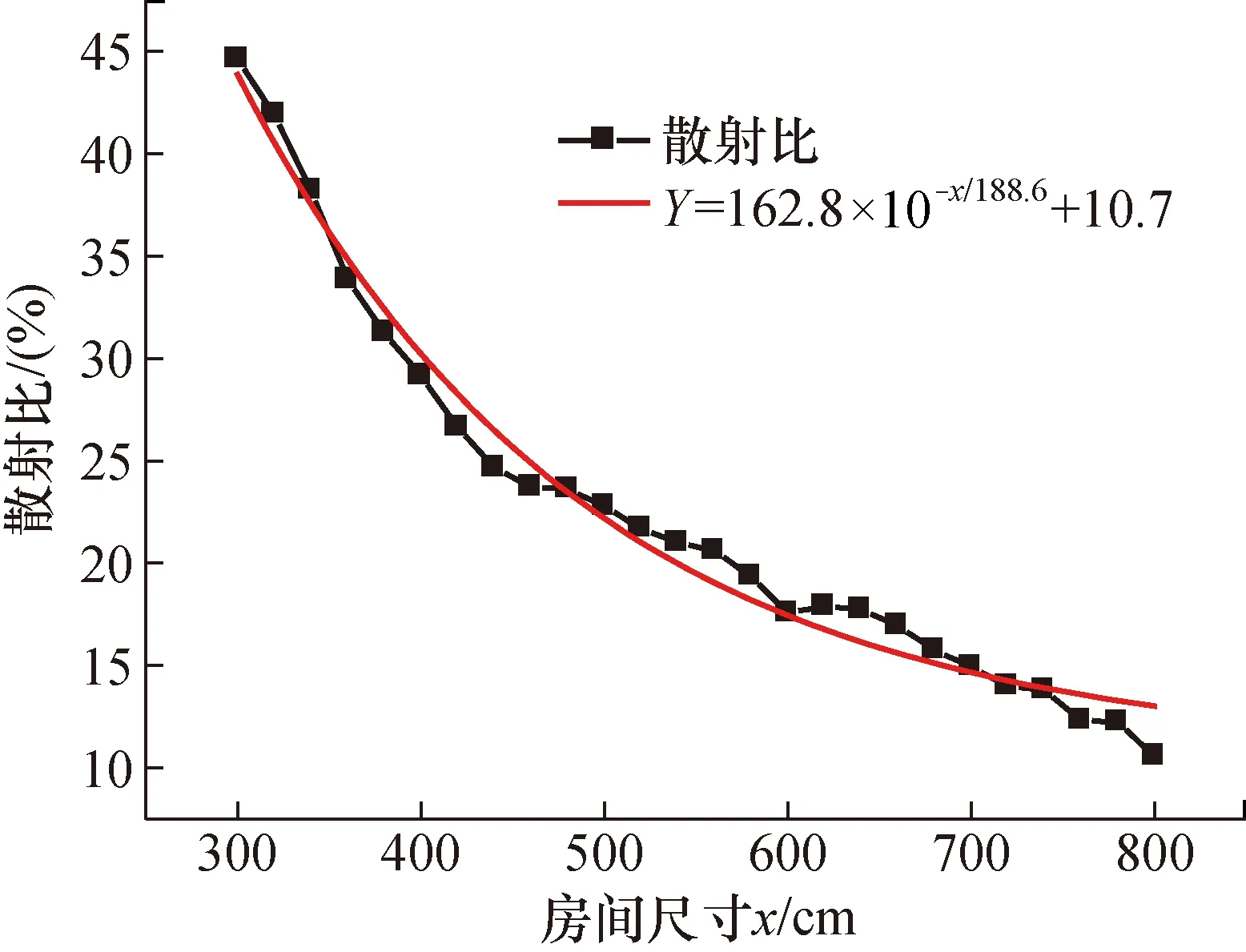
图5 长方体房间散射比变化曲线Fig.5 Variation curve of scattering ratio of cuboid room

在表5中，给出了D-D中子源进行中子周围剂量当量仪校准所需最小房间的相关参数。

表5 使用D-D中子源校准所需房间的最小尺寸Tab.5 Minimum dimensions of rooms for calibration using D-D neutron sources cm

4 结 论

本文使用能量截断法代替影锥法对产生中子能量为2.8 Mev的D-D中子源在不同类型、不同尺寸房间中的散射中子进行了计算，并由计算结果做出了不同类型房间中的中子散射比的变化曲线。通过变化曲线，得知散射中子所占比例会随着房间内部空间尺寸的增加而减小，且减小过程满足指数衰减规律。根据计算结果，若使用D-D中子源进行中子周围剂量当量仪校准，在探测距离75 cm，探测器直径20 cm，混凝土墙体厚度12 cm的情况下，所需的最小正方体房间的内部空间棱长为332 cm；所需最小长方体房间的内部空间的长、宽、高分别为410 cm、410 cm、205 cm。