一种连续性非局部变分图像修复模型

李 兰，陈明举，熊兴中，杨志文，张劲松

(1.四川轻化工大学 自动化与信息工程学院，四川 宜宾 644000；2.四川轻化工大学 人工智能四川省重点实验室，四川 宜宾 644000)

0 引言

数字图像修复技术通过相应的、适当的数学模型对图像缺损区域进行修复，以改善图像的视觉效果[1]。数字图像修复已应用在文物保护、影视制作、刑事案件的侦破以及老照片的修复等各个领域[2-3]。近年来，变分技术将图像修复问题转化为泛函空间的极值问题[4]，通过数值迭代方法有效地实现图像破损区域的修复，基于变分(Total Variation，TV)技术的图像修复技术已成为当前研究热点。

Bertalmio等[5]最早将变分技术应用于图像修复中，该方法在图像破损区域边界沿着等照度线方向扩散，从而实现利用已知的信息传播修补破损区域。随后，一些学者在此基础上提出了总变分图像修复模型[6]、几何信息驱动的曲率扩散图像修复模型[7]以及分数阶总变分图像修复模型[8]等。这些图像变分模型利用图像的结构连续性较好地实现小破损区域的修复。当破损区域较大时，图像的修复性能变差。为有效实现较大的破损区域的修复，Gilboa等人[9]利用图像的自相似性，提出了l2范数的非局部变分模型，该模型在考虑到图像信息的连续性的同时利用图像非局部的相似性有效地实现大破损图像的修复。随后，Yang等人[10]利用l1范数的异向特性，建立非局部异向扩散的图像非局部变分模型；Shi与Li等人[11-12]针对图像的修复问题，在l1范数非局部变分的基础上提出了非局部变分修复(Non-local Total Variation，NLTV)模型。图像修复的非局部变分利用图像的相似信息有效地实现大破损区域的修复，其修复性能在局部变分的基础上有一定提高。

NLTV模型实质上是将图像看作真实信息区域与破损区域2个部分，利用图像已知的信息向破损区域扩散，从而有效地实现破损区域的填补[13]。然而，该非局部变分修复模型存在考虑不足之处[14-15]：① 模型仅考虑图像破损区域的修复，未考虑到破损区域与信息区域的交界区域，从而造成修复后的图像在交界区域存在不连续性现象；② 修补过程中信息区域参与的扩散强度恒定，未充分利用信息区域的有效信息。

为了在实现图像的破损区域修复的同时，考虑到破损区域与信息区域边界的连续性，并且消除修复区域产生的“阶梯”现象，提出了一种连续性非局部变分的图像修复模型，采用罗宾边界算子[16]描述破损区域与信息区域的边界，针对破损程度的大小，实现对图像修复扩散强度自适应控制。

1 自适应连续性非局部变分修复模型

1.1 非局部变分修复模型的不足

非局部变分技术利用图像信息区域的相似信息实现图像破损区域的修复。定义P={p1,p2,…,pn}为Rd空间的图像集合，S={s1,s2,…,sn}为P的子集。待修复图像u由集合P确定，子集S的像素值已知，满足u(s)=g(s)，g(·)表示无损原始图像。图像的非局部变分修复模型利用图像的相似性与梯度的连续性实现待修复区域信息的重构，如图1所示。

图1 图像修复示意Fig.1 Schematic diagram of image inpainting

s.t.u(x)=g(x)x∈S。

(1)

上述能量泛函极小问题可以通过欧拉拉格朗日方程表示为：

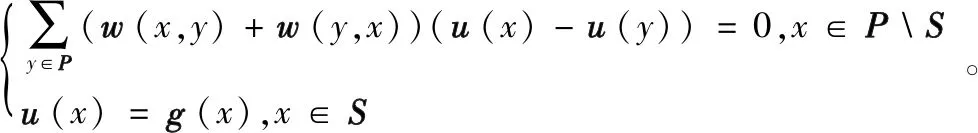
(2)

从式(2)可以看出，图像的非局部变分修复模型对于信息区域S保持不变，对于破损区域PS，采用图像的非局部梯度作为图像修复的扩散因子，利用非局部相似信息实现图像破损区域的修复。然而该方程未考虑到破损区域的边界，遗漏了破损区域与信息区域的连续性问题，从而在修复后的边界区域出现“阶梯”现象。另外，该模型修复过程中的扩散强度仅与非局部梯度有关，未考虑到信息区域参与的程度问题，因此，NLTV模型的修复性能有待进一步提高。

1.2 自适应连续性非局部变分修复模型的建立

将破损区域的边界∂B考虑进去，在式(2)中增加边界区域扩散项，欧拉拉格朗日方程可进一步转化为：

(3)

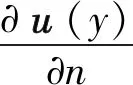
(4)

式中，μ为罗宾边界参数，其取值为0<μ<<1，上述方程组进一步表示为：

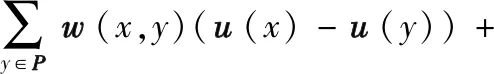
(5)

此时，式(5)欧拉拉格朗日方程对应的非局部变分修复模型为：

s.t.u(x)=g(x)，x∈S。

(6)

该非局部变分修复模型将图像的信息区域、破损区域以及边界区域都考虑，实现修复区域边界的连续性。式(6)中，信息区域变分部分乘以权值2/μ(2/μ>>1)，该项侧重于利用信息区域的相似信息实现破损区域的恢复，同时减弱交界区域的不连续现象。理论上，当图像的破损区域较大时，信息区域参与权重也应该相应地增大；反之，破损区域较小时，信息区域参与权重也相应地较小。对上述边界连续的非局部变分模型的权值参数进行修正，以实现信息区域参与权重的自适应，从而建立自适应连续非局部变分修复模型为：

s.t.u(x)=g(x)x∈S，

(7)

式中，|P|/|S|表示求图像块包含面积的个数。在该模型中，当破损区域较大时，权值|P|/|S|的值较大，这时该模型着重利用信息区域的信息实现破损区域信息的修复，以更好地重构图像破损区域的信息，从而消除分界区域不连续现象。

1.3 自适应连续性非局部变分修复模型的求解

为方便实现对自适应连续非局部变分修复模型的求解，定义：

(8)

此时，自适应连续非局部变分修复模型可进一步表示为：

s.t.u(x)=g(x),x∈S。

(9)

采用分裂迭代(Split Bregman Iteration，SBI)的思想[18]，并令D(x,y)=DNLu(x,y)，进一步转化为求解2个极小化问题：

s.t.u(x)=g(x),x∈S，

(10)

Qk+1=Qk+(DNLuk+1-Dk+1),

(11)

式(10)涉及参数u与D两个极小化问题的求解，分别转化成u与D两个变量的极小化问题：

s.t.u(x)=g(x),x∈S，

(12)

(13)

定义：

(14)

令Dx=D(x,:)，则：

(15)

D的极小化问题可以进一步分解成对D(x,:)分别求解：

(16)

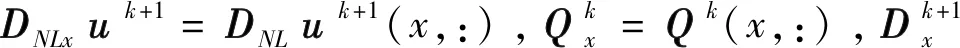
(17)

Dk+1的迭代求解为：

(18)

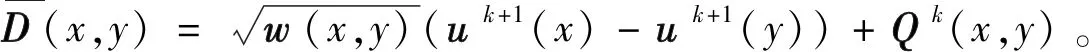
u的求解可通过式(18)的梯度为0求得：

(19)

其中，

(20)

此时，uk可以通过2FFT快速求解。

综上，图像修复的自适应连续非局部变分修复模型的SBI求解流程如下：

输入:破损图像f;输出:处理后的图像u。初始化:u0=f,D0=0,err=1,λ=γ=0.1,并计算P/S的值,破损区域填充随机像素值;Whileerr≥0.01对于图像点x,寻找其相似图像块集合;计算非局部相似系数系数;按式(18)更新Dk+1;按式(20)更新λk;利用2D-FFT求解式(19)得到uk+1;按式(11)更新Qk+1;计算误差值err=‖uk-uk-1‖2;End

2 实验结果与分析

为验证本文提出的连续性非局部变分修复模型的性能，将连续性非局部变分修复模型的修复结果与NLTV修复结果进行对比。图2给出了“Lena”图像采用2种算法修复后的结果，以及修复后图像与原始图像的差值图像。从图2中可以看出，本文提出的连续性非局部变分修复模型相对于NLTV模型更好地修复图像的信息，差值图像灰度值较小，修复后的图像更好地接近真实图像。

(a) 原真实图

为了进一步说明自适应连续非局部变分修复模型具有更好的图像修复性能，选“carriage”“temple”“parrots”“butterfly”4幅彩色图像(如图3所示)分别加入字幕、随机斑块、划痕以及方块噪声的破坏，采用NLTV与自适应连续非局部变分修复模型2种模型进行修复，修复结果如图4所示。为便于对比修复的效果，在图4中各个图的右下角给出绿色区域的放大图。

(a) 四轮马车

(a) 破损图像

对比2种模型修复的结果可以看出，自适应连续非局部变分修复模型修复后的图像细节与边缘都得到更好的重建，如，carriage图中的栏杆与parrots图中的羽毛采用ACNLTV模型修复后更清楚，temple图中的文字边界与butterfly的斑块纹理边界采用自适应连续非局部变分修复模型修复后更明显。

客观评价方面，采用Peak Signal to Noise Ratio(PSNR)峰值信噪比和Structural Similarity Index(SSIM)结构相似性作为评价指标，其中PSNR是用来评估2张图像中对应的像素点之间的误差，值越高表示失真越小。SSIM是用来评估2张图像在亮度、对比度以及结构3个方面的整体相似性，其结果越接近1表明相似性越高。图4中图片修复前后的PSNR与SSIM如表1所示。

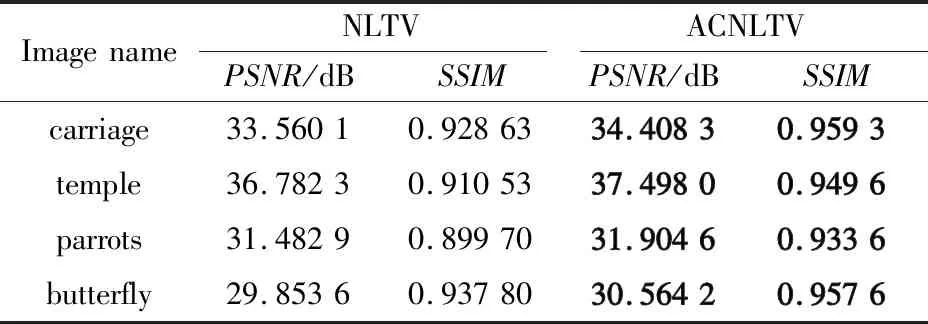
表1 不同图片2种模型修复性能比较Tab.1 Inpainting performance comparison of two models for different images

由表1可以看出，自适应连续非局部变分修复模型修复的PSNR与SSIM明显高于NLTV修复的结果，其PSNR与SSIM分别高于NLTV约为0.5 dB与0.2，从客观指标再次说明ACNLTV模型修复更优。

3 结束语

本文提出了一种连续性非局部变分图像修复模型。采用罗宾边界算子描述破损区域与信息区域的边界，并针对破损程度的大小实现对图像修复扩散强度自适应控制，从而提出连续性非局部变分的图像修复模型，并给出了该模型的交替极小化求解过程。在试验中，通过与NLTV模型对比分析，证明本文提出的连续性非局部变分的图像修复模型在图像修复过程中更好地修复图像的细节信息，峰值信噪比更高，图像修复性能更明显。因此，本文提出的连续性非局部变分的图像修复模型具有很好的应用前景。