适用于深空探测器的时间线转移路标启发式规划方法

金 颢，徐 瑞，朱圣英，李朝玉，梁子璇

(1. 北京理工大学深空探测技术研究所，北京 100081；2. 深空自主导航与控制工业和信息化部重点实验室，北京 100081)

0 引 言

航天器自主任务规划技术的发展很大程度上缓解了复杂航天器系统人工决策的压力[1-2]。它能够根据任务设定的目标，按照一定的行为推理方式，给出符合规则的可行活动安排[3-5]。这种自主决策方式使得地面人员得以从繁重的指令编排工作中解放出来，能够在保障航天器平稳运行的同时节约任务成本[6-8]。

深空探测任务的难度与日俱增，愈发复杂的物理系统导致传统建模方法已经无法满足其知识描述的需求。探测器各子系统的行为是随时间变化的函数，故探测器任务规划需要一种更为简洁且表达力强的形式对问题域进行描述。另外，系统功能的多样性会增加模型的复杂度，甚至影响规划算法的决策。例如，火星车上存在两个可交替使用的加热设备用于现场试验。这种情况为规划器提供了更多样化的选择，会增大局部搜索范围，增加规划时间。因此，需要更有效的搜索引导策略来提高规划的效率，在短时间内获取一个正确的可执行活动序列。

自主规划技术在航天中的应用一直是学术讨论的热点，并且已有部分方法在航天任务中得到了成功的应用。可扩展的通用远程规划框架(Extensible universal remote operations planning architecture, EUROPA)在NASA“深空一号”任务中得到了在轨应用，完成了自主任务规划技术的星上验证。EUROPA将规划过程中复杂的约束关系统一表示为token之间的时间约束，并采用基于约束的搜索策略进行规划求解，优化了规划问题的描述方法[9-11]。但是，它所采用的深度优先搜索算法，在搜索节点的选取和扩展方面缺乏合适的评价方法，会对规划效率产生一定程度的影响。自主科学飞行器实验(Autonomous science experiment, ASE)是地球观测1号(Earth observation 1, EO-1)的星载自主软件[12]。ASE通过调用连续活动规划执行和重规划(Continuous activity scheduling planning execution and replanning, CASPER)软件，能够根据星载科学分析模块提供的目标自动生成任务规划活动序列。CASPER采用基于迭代修复技术的规划算法，同时还应用启发式方法在选择修复策略时排除不相关的搜索选项。但是，该启发式方法主要关注于不同修复冲突方法的比较，而鲜有对当前部分规划中所有可选活动的评价。先进规划调度框架(Advanced planning and scheduling initiative, APSI)是设计应用于火星快车任务的规划系统。ASPI的开发是为了提高人工智能规划和调度工具开发的效益和灵活性[13]。APSI采用基于迭代缺陷的方法，在选择缺陷时使用启发式策略削减搜索空间，但在缺陷求解步骤方面并未做深入的研究。王晓晖、李爽针对深空探测器任务规划方法在处理系统间复杂约束时存在的约束复杂度高、计算效率低等问题，提出一种新的约束简化方法和启发式连续任务规划方法[14]。牟帅等针对空间站在轨运营出现突发任务的情况，考虑活动间复杂约束关系传播的影响，提出时间回溯迭代冲突化解策略完成对原任务执行序列的重规划[15]。为了更好地应对航天器日益复杂的任务需求以及可能的外部干扰信息，规划器需要具备在短时间内形成正确决策的能力。因此，规划搜索的效率就显得尤为重要。通过在搜索中加入启发式评价，能够辅助规划器删除错误或不“明智”的决策，实现加速求解的目的。

在启发式评价技术方面，各类思想相互碰撞，方法策略层出不穷。其中，基于路标的方法由于其在搜索引导方面效果显著，自Porteus等[16]提出了第一种利用事实路标的规划算法后，迅速发展壮大成为启发式搜索中的一个重要分支。Karpas和Dom-shlak首次提出了析取动作路标的概念[17]，Helmert和Domshlak在该概念的基础上提出了著名的Landmark-cut方法[18]。随后，Blai[19]、Pommerening等[20]、Röger等[21]和Seipp等[22]都纷纷对这些方法进行了改进。然而，这些研究都集中于状态空间中的启发式设计，对于时间线规划方向鲜有涉及。因此，本文将路标思想与时间线规划相结合，设计一种时间线转移路标启发式评价策略，提高规划搜索的效率。

文章主要结构如下：第一节对时间线规划及路标相关的基础知识进行了解释；第二节设计了一种时间线知识框架下的hmax评价方法；在该方法的基础上，第三节提出了时间线路标提取方法以及时间线转移路标启发式规划算法；第四节进行了仿真实验，对比讨论分析各算法的性能；最后对所有内容进行了总结，得出结论。

1 基础知识释义

深空探测器时间线转移路标启发式规划方法使用时间线知识描述模型，并在其基础上进行启发式算法研究。为了便于后文的描述，首先解释几个基本概念。

对hmax评价图进行消环处理，需要尽可能的不影响到路标迭代搜索的过程，保证更多的路标存留。由于析取状态路标的搜索是通过在初始状态顶点到目标顶点的转移路径上不断选取必要的析取状态集合，所以对于存在环路的状态转移路径，删除其他状态转移到初始状态的边，既实现了转移路径消环，又不会对该搜索过程产生影响。如图4所示，图(a)中中心状态I为初始状态，其他状态与状态I之间均存在双向转移，所以该状态转移存在闭环。根据规则1可知，需删除所有转移到初始状态I的边，图(b)中的“放射状”转移即为消环后的转移图。

状态变量是对深空探测器系统知识的抽象，它能够表示探测器的某个分系统、设备或某种资源在一段时间内的变化。状态变量x可以表示为一个三元组x=，其中：V表示状态变量x的值域，是一个非空集合；T表示状态变量值域空间中所有取值之间的转移规则；D表示状态变量所有取值的持续时间。

状态s是状态变量在某个时间点或时间区间上的取值，可表示为一个三元组s=，其中：ts、te和d分别表示状态s的开始时间、结束时间和持续时间。并且，由于深空探测任务中环境的不确知可能影响规划序列的正常执行，将状态s的所有时间参数均定义为一定的时间区间，即ts=[tsl,tsu]、te=[tel,teu]以及d=[dl,du]。通过获取鲁棒性更高的规划解来应对执行过程中可能出现的不确定性问题。

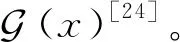
析取状态路标：假设存在状态集l，若集合l至少存在一个状态在规划任务Π的所有可行解中均为真，则该状态集l被称为规划任务Π的一个析取状态路标。

根据上述方法将深空探测器描述为离散、并行的状态转移系统，然后针对该系统设计提出合适的启发式规划方法。时间线转移路标启发式规划方法是建立在hmax评价方法的基础上。因此，下一节中首先提出了时间线规划中的hmax评价方法。

2 时间线规划hmax评价方法

2.1 规划问题实例

首先，给出一个简化的深空探测器任务规划问题实例。某巡视探测器的任务包括采样和简单的现场试验，试验步骤为对样本进行加热并在加热的过程中采集数据。该实例的规划模型中共包含两条时间线：采样设备时间线和加热设备时间线。各时间线的状态转移如图1所示，两个设备之间的约束仅考虑加热状态与采样状态的时间关系：加热需在采样之后。任务开始时采样设备处于卸载状态，加热设备处于关机状态，任务目标为完成一次现场试验。

2.2 最大约束转移代价计算

时间线规划hmax评价方法通过计算时间线上目标的转移代价估计状态到目标的距离，并以此作为节点的启发式评价。时间线Lx上状态s1到s2的转移代价由两部分构成：

J(s1,s2)=max(αJT,βJC)

(1)

其中:αJT为该状态转移影响时间线Lx内部状态分布所带来的代价，JT表示转移路径中实际转移的数量，α为比例系数表示内部转移代价的影响因子；βJC表示该状态转移对其他时间线的影响，JC为各段状态转移条件的代价，β为比例系数表示转移条件代价的影响因子。

如图1所示，该探测器在进行试验前需要先完成采样任务，即“采样”状态需要在“加热”状态之前。那么，加热设备时间线上所有到“加热”状态的转移都需要满足采样设备时间线上完成“采样”状态这一约束条件。因此，采样设备时间线上的状态分布，会影响到加热设备时间线上状态转移的代价评估。

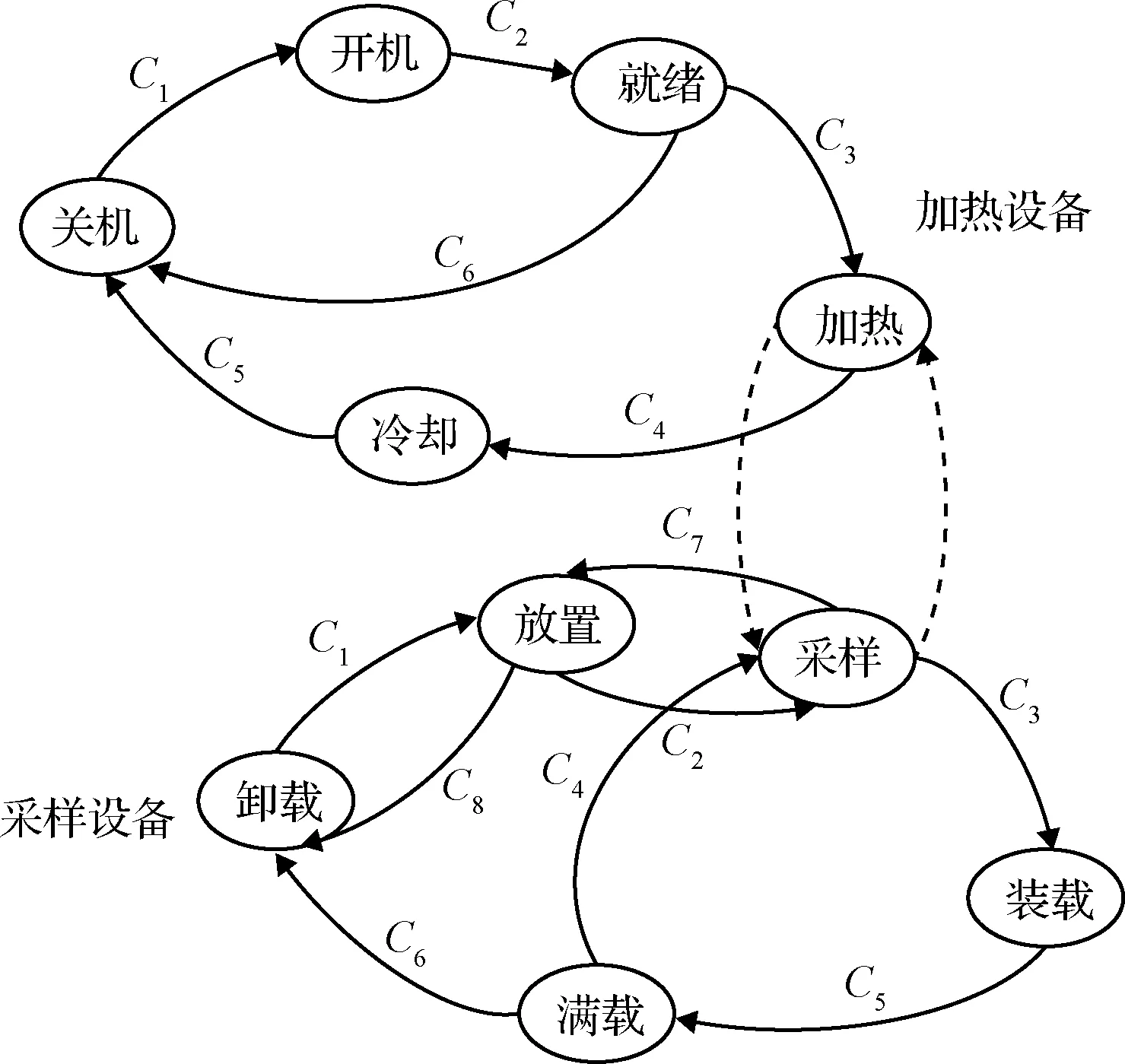
图1 采样设备和加热设备状态转移图

由于转移条件可能涉及其他时间线的状态，即实现时间线Lx上的某个状态转移，需要其转移条件s′∈x′所在时间线Lx′的取值为对应该转移条件s′∈x′的状态s′。所以转移条件代价受该时间线状态分布的影响——时间线Lx′上当前状态s*到状态s′的转移代价。然而，时间线规划中采用的偏序搜索模式和节点中大量时序并行的状态使得获取准确的转移条件代价会占用大量的计算资源。为简化计算过程中的时序处理，使用初始状态[22]作为s*的替代进行转移条件代价计算。

若某段转移的转移条件集合中存在多个状态，如s′和s″，则分别计算各转移条件的代价后选择其中的最大值作为该段转移的条件代价，即最大约束转移代价：

JC=max(J(Is′,s′),J(Is″,s″)) (2)

图2 最大约束状态转移代价算法

Fig.2 The maximum transitioncondition algorithm

其中:Is′和Is″分别表示状态s′和s″所在时间线的初始状态。算法如图2所示，这里取系数α=β=1，表示内部转移与外部条件对整体转移代价影响的比例相同。

2.3 时间线hmax节点评价

时间线规划算法的输入为问题的初始状态集合和目标条件集，输出是满足所有约束的由各初始状态到目标状态的转移路径集合。规划器在目标集合G中挑选合适的目标(或子目标)状态g∈G实例化到部分规划中，经约束传播并满足一致性条件后，将目标(或子目标)状态g的所有约束作为子目标加入G{g}，更新目标集合。迭代上述过程，当目标集合G为空时，算法停止，并得到该问题的一个规划解(否则该问题无解)。

在石英岩、片麻岩、片岩、变粒岩中，石榴石广泛发育，十字石常与蓝晶石和石榴石共生；黑云变粒岩及黑云片麻岩中常可见到矽线石；蓝晶十字黑云变粒岩、黑云母石英片岩及黑云母片岩中均有堇青石出现，这些都是典型变质特征矿物，反映变质相为中低变质相，即角闪岩相。

时间线hmax节点评价方法采用上文所述的最大约束代价法计算得到各目标(不包含子目标)的评价值，并选取其中最大的评价值作为当前节点的代价。若目标g存在析取约束集合C1(g)和C2(g)，则分别计算各约束集的最大约束代价值，并选取其中最小的代价作为该目标的启发式评价。在规划过程中，规划器会调用启发式函数计算所有候选节点的评价值，选择其中评价值最小的节点完成扩展。

观察组患者用药后，复发率为17.95%(7/39)，进展率为2.56%(1/39)；对照组患者用药后复发率为23.08%(9/39)，进展率为5.13%(2/39)，两组间比较无明显差异(P>0.05)不具备统计学意义。

时间线hmax节点评价流程如下所示:

1)在目标集合G中选择状态g∈G,G:=G{g}；

对于我国社会发展而言，其拥有全球最广阔的工业机器人应用市场，并且随着我国工业产业结构的转型升级和人口红利的退减，导致的中国机器人应用市场的快速发展。并且可以预见在未来我国工业机器人的范围和使用将会呈现出柔性化、智能化等方向发展。

2)搜索与g位于同一时间线的初始状态Ig；

3)计算状态转移代价J(Ig,g)；

5)重复2～4，直到N*中包含初始状态顶点，停止；

5)返回所有代价的最大值。

3 时间线转移路标启发式

由于深空探测器具有系统复杂、约束耦合以及时序并行的特点，经典规划方法难以对深空探测任务进行规划求解。而且，复杂的模型信息导致规划搜索过程中搜索空间急剧膨胀，严重影响了规划求解的效率。针对这一问题，从启发式设计的角度出发，围绕状态路标的提取及动态更新、状态路标代价计算以及最大路标集合节点筛选策略等方面进行研究，提出了时间线转移路标启发式规划方法。通过快速准确地评估搜索空间中的候选节点，实现无关节点剪枝、削减搜索空间以及加速深空探测任务规划求解的目的。

3.1 时间线规划路标提取方法

3.1.1构建hmax状态评价图

以聚氯乙烯和煤焦油为主要原材料，掺入适量的外加剂，以水为分散介质而制成的水乳型防水涂料，称为聚氯乙烯防水涂料。聚氯乙烯防水涂料在施工应用中，也需要铺设玻璃纤维布或聚酯无纺布等材料进行增强处理，以达到增强的效果。

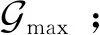
1)选择一个状态s∈x约束集中的状态s′；

2)计算J(Is′,s′)；

3)重复1、2，遍历整个约束集；

3.2.1状态路标代价计算

2.规范抗晕训练和运动中操作训练：海上医疗人员的晕船、操作不精准等可通过陆地抗晕训练和运动中操作训练来强化克服。在医院平时的陆地训练中，一方面加强体能训练，提高身体素质，同时通过滚轮、浪木等器材进行前庭功能训练，增强抗晕能力。另一方面可通过在行驶车辆中练习静脉穿刺等方法来提高运动中操作的精准度。医务人员在陆地训练的基础上，通过海上适应性训练熟悉船体摇摆、颠簸、振动条件下的技术操作要领，掌握患者、固定装备和操作者的三方固定方法，可以强化海上操作行为的准确性和安全性，降低职业暴露风险。

全部状态的约束集合经过上述“变形”，都映射为评价图中的点和边的集合。从而，状态评价图中初始状态到目标状态的所有路径的必经顶点集合表示所有规划解中必然存在的状态。所以，规划任务的一个析取状态路标l可以表示为评价图中的一个顶点集合Vl，使得评价图中所有从初始状态集合到目标集合的路径均至少包含集合Vl中的一个顶点。因此，在评价图中搜索所有具有上述性质的顶点集合，可得到规划任务的状态路标集合M。根据评价图的特点可知，包含全部顶点的集合一定是满足上述约束的一个顶点集合，所以对于任意状态评价图，顶点集合一定存在且不为空集。为了获取尽可能多的路标集合l完成对规划搜索的评价，提出多目标迭代扩张算法进行路标搜索。

正说着，一个小媳妇袅袅娜娜地走过来，她端着盆，是来河边淘米的。老砍头见她来了，低下头，四处望。小媳妇笑着问：“一大早的在找什么呢？”

3.1.2多目标迭代扩张路标搜索算法

对于目标g∈G，考虑评价图中存在的两类区域，一是能够通过代价为0的路径到达目标g的顶点集合N*，另一区域为初始状态的所有可达顶点集合中与N*不相交的部分NI。由于评价图中由初始状态到达目标状态的转移路径必然包含区域N*中的顶点，则所有由NI指向N*中顶点的边集El即为规划解中必需的状态转移。从而，集合El中各边指向的顶点构成了一个析取状态路标l，路标l的代价为El中的最小转移代价。将El中所有转移的代价分别减去l的代价并对应更新到评价图中，完成路标l对评价图的代价划分。由于代价划分可能导致出现新的代价为零的边，所以需要对集合N*和NI进行更新，这样就实现了集合N*的一次“扩张”。重复上述步骤，迭代扩张集合N*，直到找到从初始状态顶点到目标顶点的一条代价为0的路径。具体步骤如下所示：

1)初始化集合NI、N*；

质谱条件:Agilent HP-5色谱柱(25 m × 0.32 mm × 1.05 μm); 柱流量:1 mL/min; 质量范围:29～420 AMU; 电子倍增电压(EMV):1 435 V; 电离电压:70 eV; 离子源温度:230 ℃; 四极杆温度:150 ℃。

2.讨论形成方案。将学生分为10个小组，以小组为单位进行讨论，研究制订相关方案，方案内容包括了解雾霾的严重性、成因、解决措施以及对应的英语词汇。

2)搜索由NI指向N*的边集El；

该区域加深钻井采用高密度钻井液支撑井壁，提高抑制性能防止泥页岩水化分散脱落，并选择合适钻井工艺防塌措施的施工方案。以152井为例，该井钻井液密度控制为1.85～1.90g／cm3，漏斗黏度为50～70s，pH值为9～11，切力为（8～12）／（15～20）Pa／Pa，动切力为12～16Pa，塑性黏度为25～35mPa·s，常规滤失量为3～5mL，高温高压滤失量（150℃）为8～10mL，固相含量36%～40%，含砂量为0.3%～0.5%。

经hmax评价图构建、消环和路标提取过程后，得到规划任务Π的析取状态路标集合M。假设图中转移边的代价均相等，则多目标迭代扩张路标搜索算法如图6所示。下一节将集中讨论如何有效的利用析取状态路标集合M加速规划搜索。

4)更新集合NI、N*；

4)重复1～3，直到G为空集，停止；

6)提取析取状态路标集合M={l1,l2,…,ln}。

如图3所示，评价图中顶点g为目标状态，I1和I2为初始状态，图中边的权值均为0或1。则由步骤1得到的集合N*={C，E，F，g}(图中实心圆表示的顶点)，NI={I1，I2，A，B，D}(图中空心圆表示的顶点)。然后搜索从NI到N*的边集El={，}，并提取El对应的析取状态路标l={C，E}，代价为1。将评价图中的边，的权值减去1后，重新搜索集合N*={B，D，C，E，F，g}，NI={I1，I2，A}。迭代上述过程，得到该评价图对应的析取状态路标集合为：M={{C，E}，{B，D}}。

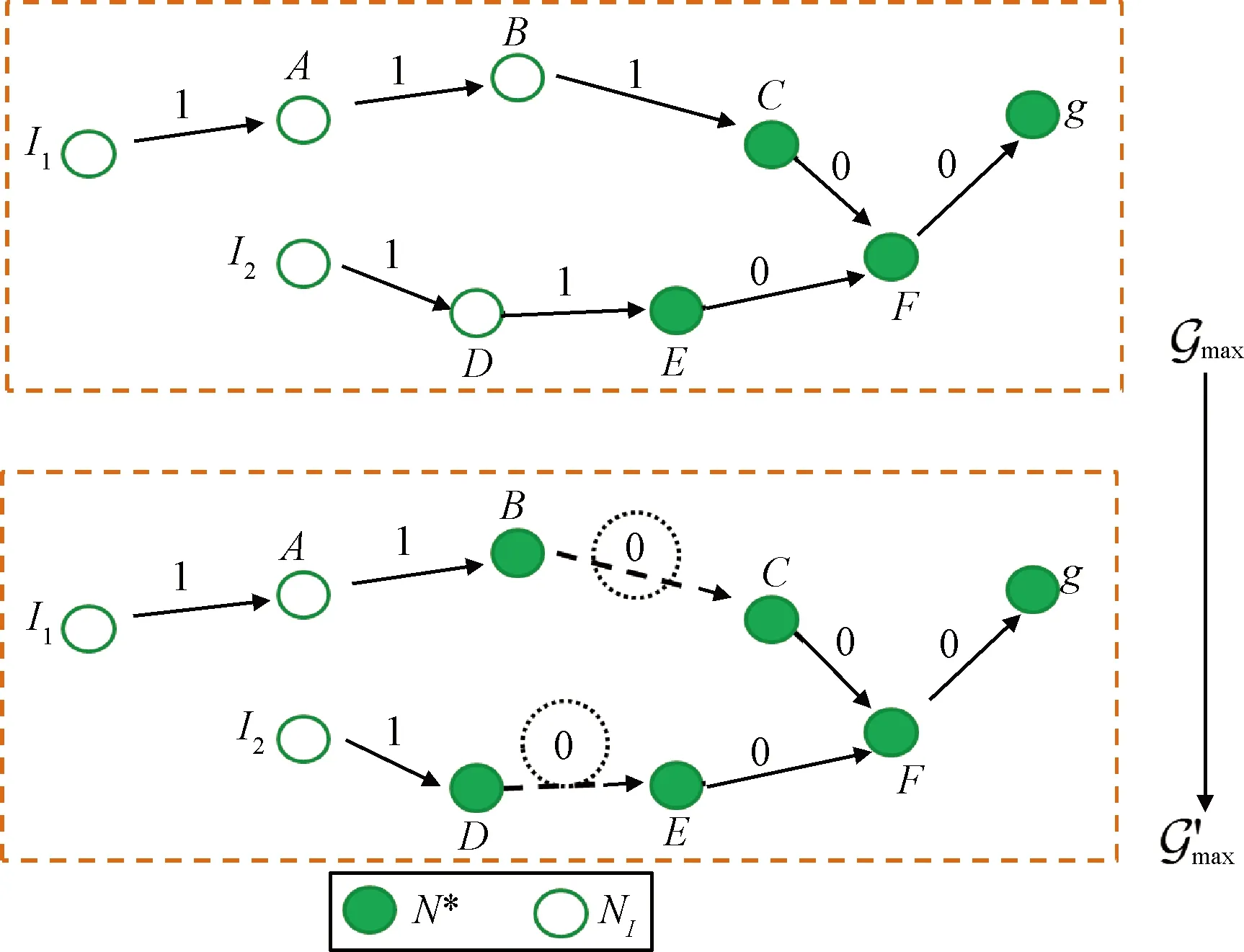
图3 评价图中N*集合的一次扩张

通过上述步骤1～6，可计算得到目标g的析取状态路标集Mg。为了进一步增强路标对规划搜索过程的控制，需要获取尽可能多的析取状态路标对节点进行更准确的评估。因此，将集合G中的全部目标作为上述路标提取步骤的输入，对任意g∈G，建立独立的评价图进行计算，最终得到各目标的析取状态路标集合M=∪Mg, ∀g∈G。通过实现析取状态路标对规划任务全部目标的覆盖，引导规划搜索过程中各目标最短转移路径的建立，加速规划求解。

由于多目标迭代扩张算法是对评价图的节点集合迭代划分的过程，若评价图中出现环路，则该算法可能陷入重复计算而导致求解失败。因此，需要对状态评价图进行去环。考虑模型约束对hmax评价图的影响，设计了如下时序转移消环策略：

1)若某时间线的状态转移形成一个大的闭环，则在初始状态处进行切断，即删除转移到初始状态的边；

2)若某时间线的状态转移形成局部闭环，删除向靠近初始状态方向转移的边。

一个深空探测规划任务为一个四元组Π=，V为状态变量集合，C表示约束集，I⊆V为初始状态，G⊆V为目标集[23]。

固本拓新--基于传统住宅的装配式住宅建筑设计…………………………………………………… 彭敏，万莉（7-18）

4.3 化学防治 2017年我们进行了大生M-45、多霉清、复方多菌灵、甲基托布津等杀菌剂防治金丝小枣浆烂果病对比试验。结果表明，不同药剂防治金丝小枣浆烂果病效果差异显著，其中800倍液80%大生M-45防效最好。

图4 整体闭环的转移图消环

同理，目标g2和g3的距离估计值分别为hg2和hg3。综合各目标的评价值，为避免出现节点过评估的情况，选取其中的最大值作为节点N的评价值。

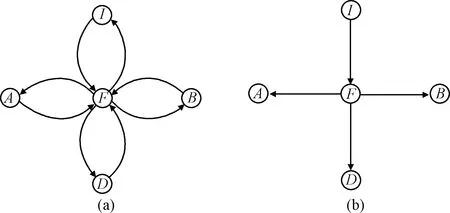
图5 转移图中局部回退边消环

3)提取析取状态路标l，完成l的代价划分；

图6 多目标迭代扩张路标搜索算法

3.2 深空探测器时间线转移路标启发式规划算法

4)只保留最大代价的约束s′max。

启发式方法是基于规划问题的目标集合，给出一定的规则来评价一个状态的代价。例如，快速正向(Fast forward，FF)搜索算法通过生成一个从当前状态到目标的松弛规划解来估计该状态到目标的距离，然后将生成的规划解中的动作数量用作启发式评价。同理，针对深空探测规划任务Π，利用上一节计算得到的析取状态路标集合M进行启发式评价能够保证规划器优先选择规划解中必然存在的状态，从而，进一步实现对无关节点的剪枝，削减规划问题的搜索空间。

时间线规划路标提取方法实现了对各目标状态析取路标的独立搜索。故对于目标gi∈G，存在析取状态路标集合Mgi与之对应。假设节点N∈N扩(N扩表示下一步可扩展的候选节点集合)中存在目标g1、g2和g3，以及各目标的析取状态路标集合Mg1、Mg2和Mg3。更全面准确的评估节点N需要综合其全部目标的距离信息。对于目标g1，节点N中的析取状态路标集合Mg1既包含了到目标g1的最短转移路径节点，又记录了途经该节点需付出的代价。从而，节点N中目标g1的距离估计值可表示为g1在该节点的析取状态路标集合Mg1中的所有析取状态路标的代价和，即：

hg1=Σc(li), ∀li⊆Mg1

(3)

第二条规则针对转移图中的局部“回退”边进行处理。hmax评价图中对目标距离的估计值为初始状态顶点到该目标顶点的最短路径距离。而转移中的回退边(即朝向靠近初始状态方向的转移)会导致局部环路，干扰路径搜索。从而，通过删除图中的回退边进行消环，既能够有效防止搜索陷入局部循环，又能够尽量降低对目标最短路径距离的影响。如图5所示，图(a)中状态I为初始状态，中心状态F与其他状态之间均存在双向转移，所以该图存在局部闭环。根据规则2删除图中的回退边得到图(b)，完成对原图的消环处理。

h(N)=max(hgi), ∀gi∈G

(4)

析取状态路标l表示在所有规划解中都为真的状态集合。由于hmax评价图中各边具有相同的代价，节点N的评价值越低，其包含的析取状态路标数量可能就越少，规划过程中需要实例化的状态数量可能就越少。因此，在规划节点扩展过程中，需计算下一步所有候选节点的评价值，并选择其中评价值最小的节点进行扩展。

3.2.2状态路标增量式更新方法

选择评价值最低的节点完成扩展后，需要更新其所有候选节点中的析取状态路标集合。由于每次扩展节点后都会涉及大量候选节点路标集合的更新，若每次更新都对节点中的所有目标执行重新构建hmax评价图、消环和路标提取的流程，虽然能够得到更准确的路标集合和节点评价，但同时会引入大量的计算消耗，与加速搜索的初衷背道而驰。若是不更新候选节点的路标集合，则随着规划过程的进行，节点的析取状态路标集合对其目标距离估计的偏差会越来越大，甚至还有可能给出“错误”的估计结果。为了保证评价准确性的同时尽可能地降低不必要的计算耗时，采用路标增量式更新方法(见图7)，在规划过程中动态更新各候选节点的析取状态路标集合。

图7 路标增量式更新方法

假设候选节点N中新实例化的状态为sn，则目标g的析取状态路标集合Mg的动态更新流程如下：

2)删除路标集合lj；

佛陀是怎么回答的呢？用我们今天的话说，就是我们平时所经历的各种身心的烦恼，就好像一支支利箭向我们射来。比如，在病中的人，要承受身体的痛苦。而这个时候，人往往会忧虑，担心自己的病不知什么时候好，担心自己耽搁了工作，担心不能照顾好小孩，等等。这样，他所承受的就不只是身体有病的痛苦了，而是在这个痛苦之上又添加了一重痛苦。如果说身体最初的痛苦，是射向我们的“第一箭”，那么后来添加的痛苦，就是“第二箭”了。

由于lj为析取状态路标，则所有规划解中均至少包含一个lj中的状态。当实例化状态sn后，该路标得到满足，所以在Mgi中删除lj。同时，由于lj中的其他状态不再为目标gi的析取状态路标，所以将对应状态的权值加回图中，在新图上搜索是否存在新增的析取状态路标集合。

3.2.3最大路标集合节点筛选策略

针对搜索空间中的每个候选节点，状态路标启发式需要分别计算每个节点中各目标对应的状态路标集合，然后取其中最大的代价作为每个候选节点的启发式评价。这种多目标综合评价的模式虽然能够加强状态路标对整个搜索过程的控制并提高启发式评价的准确性，但同样会带来极大的计算负担。为了平衡状态路标启发式的计算消耗和评价准确度二者的潜在收益，在规划搜索过程中，对候选节点集合进行初步筛选，尽可能地降低需要计算状态路标集合的节点数量。

将当前局部规划中目标距离估计值最大的目标记作gmax，目标gmax的状态路标集合记作Mgmax。考虑采用状态路标集合进行启发式评价时的两个重要特征：首先，候选节点的启发式评价值越低，表示该节点距离规划问题的某个可行解越近，故优先选择评价值最低的节点进行扩展；其次，由于候选节点的启发式评价值为全部目标距离估计的最大值，所以若候选节点中新实例化的状态不是Mgmax中的状态，则该候选节点的代价肯定不低于hgmax，其中hgmax为Mgmax中所有状态路标的代价和。只有当候选节点中对Mgmax中状态进行实例化，才有可能进一步得到更低的评价值。

例如，表1中列出了某局部规划中所有目标的状态路标集合及各状态路标集合的代价值。假设该局部规划的所有候选节点均能够实现一个或多个状态路标集合中的状态路标(由于与状态路标集合无关的节点不会影响到状态路标集合的代价，这里仅考虑能实现状态路标的候选节点)。由表中数据可知，目标g1为当前局部规划中距离估计值最大的目标gmax，状态路标集合Mg1即为Mgmax。表中每一个状态路标集合都对应一个候选节点集合，该候选节点集合中的节点能够实例化对应状态路标集合中的状态，即实现对应集合内的状态路标。由于所有候选节点均与一个或多个状态路标集合相关，则对表中任意候选节点进行扩展必然会引起相关状态路标集合中状态路标的改变，进而影响状态路标集合的代价。然而，候选节点的启发式评价为该节点中所有状态路标集合的最大代价，所以若实例化的状态不属于最大状态路标集合，则不会减少节点的评价值。例如，节点nd2中实例化了状态路标集合Mg2状态，但由于最大路标集合Mg1中的状态路标数量不会减少，所以节点nd2的评价值不会低于原节点的评价值。

表1 状态路标集合代价及对应候选节点示例

因此，使用状态路标集合Mgmax对所有候选节点进行筛选，既能够削减当前局部规划的搜索空间，又能够在避免大量计算的同时优先挑选评价值最低的候选节点进行扩展。在搜索过程中优先选取实例化Mgmax中状态的候选节点进行进一步评价，能够加速规划器朝候选节点评价值降低的方向搜索，更容易得到规划问题的一个可行解。另外，若存在多个gmax，则采用随机策略在代价相同的目标中进行挑选。

综上，深空探测器时间线转移路标启发式规划算法如图8所示。

图8 时间线转移路标启发式规划算法

4 仿真校验

为验证深空探测器时间线转移路标启发式算法的性能，在EUROPA2的基础上分别对时间线hmax启发式规划算法和时间线转移路标启发式规划算法进行实现，并构建火星车测试场景对上述两种规划算法进行仿真测试。

该测试场景中，火星车通过钻机打孔的方式能够采集火星地表不同深度的样本。每次钻孔取样都会在三个不同的深度获取土壤样本：表面土壤样本、20 cm深的土壤样本以及50 cm深的土壤样本。在三种样本中选取一种作为收集的土壤取样，其他样本均用于现场试验。此外，火星车还能够使用星载照相机采集火星地表图像数据，并通过数据分析模块检测提取图像特征。这些收集的数据信息经压缩后存入火星车的数据缓冲区，并能够在合适的时候上传数据至轨道器中。测试场景的详细模型信息见表2。

表2 火星车测试场景详细模型信息

通过改变火星车初始位置、设备状态以及任务目标，构建十个该火星车场景的测试用例。测试问题依编号顺序目标数量逐渐增多。实验中对每个测试问题均统计其十次计算的平均值，所有计算结果如图9到图12所示。图中hmax启发式算法表示时间线hmax启发式规划算法，LM(Levenberg-Marquardt)启发式算法表示时间线转移路标启发式算法。不失一般性，将前者简略称作hmax算法，后者称作路标算法，Europa2算法称作原算法。

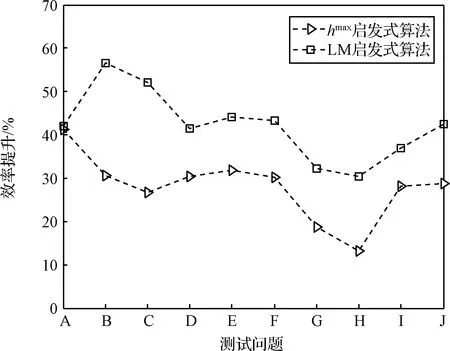
图12 规划效率提升对比图

仿真测试环境为：Windows 7 64位操作系统，i3-2350M CPU，主频2.30GHz，内存4.00 GB。图中的所有数据均为使用同等环境下原算法的计算结果减去两种启发式算法的结果得到的差值。

针对所有测试问题，启发式算法的计算时间均小于原算法的计算时间，且两种启发式算法中，路标算法的用时更少，如图9所示。随着测试问题目标数量的增加，启发式算法计算时间的优势虽然在部分问题上有所回落，但整体仍呈现上升趋势。另外，在对复杂问题进行规划求解时(如问题I、J)，启发式算法的优势更大，且涨幅更明显。如图5中计算时间曲线所示，自问题H后，曲线斜率陡增。hmax算法虽然在问题J处时间差值涨幅略缓，但与前面测试问题相比(问题A到问题G)，曲线斜率仍有较大提升。而路标算法在问题J处的计算时间差值仍然保持较高增长，甚至与问题I处相比曲线斜率仍有微弱提升。从而，在降低算法规划时间方面，路标启发式算法全面压制了hmax启发式算法。针对所有测试问题的规划求解，路标启发式算法的表现更稳定，效果更好，用时更少。

矿区内V-04、V-38、VI-09、VI-11、VI-16、VI-17、VI-20、VI-218个矿体为前5年开采矿体。

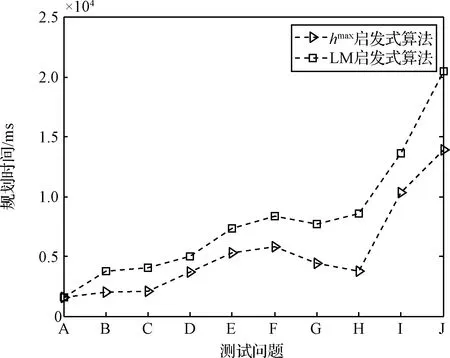
图9 规划时长差对比图

为进一步讨论和验证启发式算法的性能，探究启发式算法时间优势的缘由，对所有测试问题中两种算法的规划步数进行了统计，得到两种启发式算法相对原算法的规划步数差值曲线。如图9所示，两条曲线与图5中的计算时间差值曲线呈现出类似的增长变化趋势，但整体而言增长幅度低于时间差值曲线。hmax算法前期步数差值增幅不大，曲线平缓，问题E后曲线逐渐下降，于问题H处下降至最低点后“反弹”。虽有稍许回升但在问题J处再次回落，整体趋向于在某值附近稳定。

路标算法曲线虽然亦有两处“凹陷”，但整体变化较为平缓，且在问题J处仍呈现一定的上升趋势。二者虽然在问题A处的步数优势相同，但随着问题复杂度的提高，hmax算法在问题J处只提高约一倍的步数差，而路标算法在问题J处的步数差值约为问题A处的4倍。

同时，计算时间和规划步数之间并不是简单的线性关系。随着规划步数的增长，参与约束推理的节点数也就越多，由于原算法使用时间约束网络进行约束一致性检测，当网络中顶点数量到达一定基数时，每一步的增加都会带来大量的计算耗时。因此，图10中的曲线走势较图9而言略显平缓。规划步数差值曲线是对间差值结果曲线的有力支撑，反映出路标启发式算法的表现要整体优于hmax启发式算法。下面进一步讨论规划步数中节点扩展数量的差异对规划结果的影响。

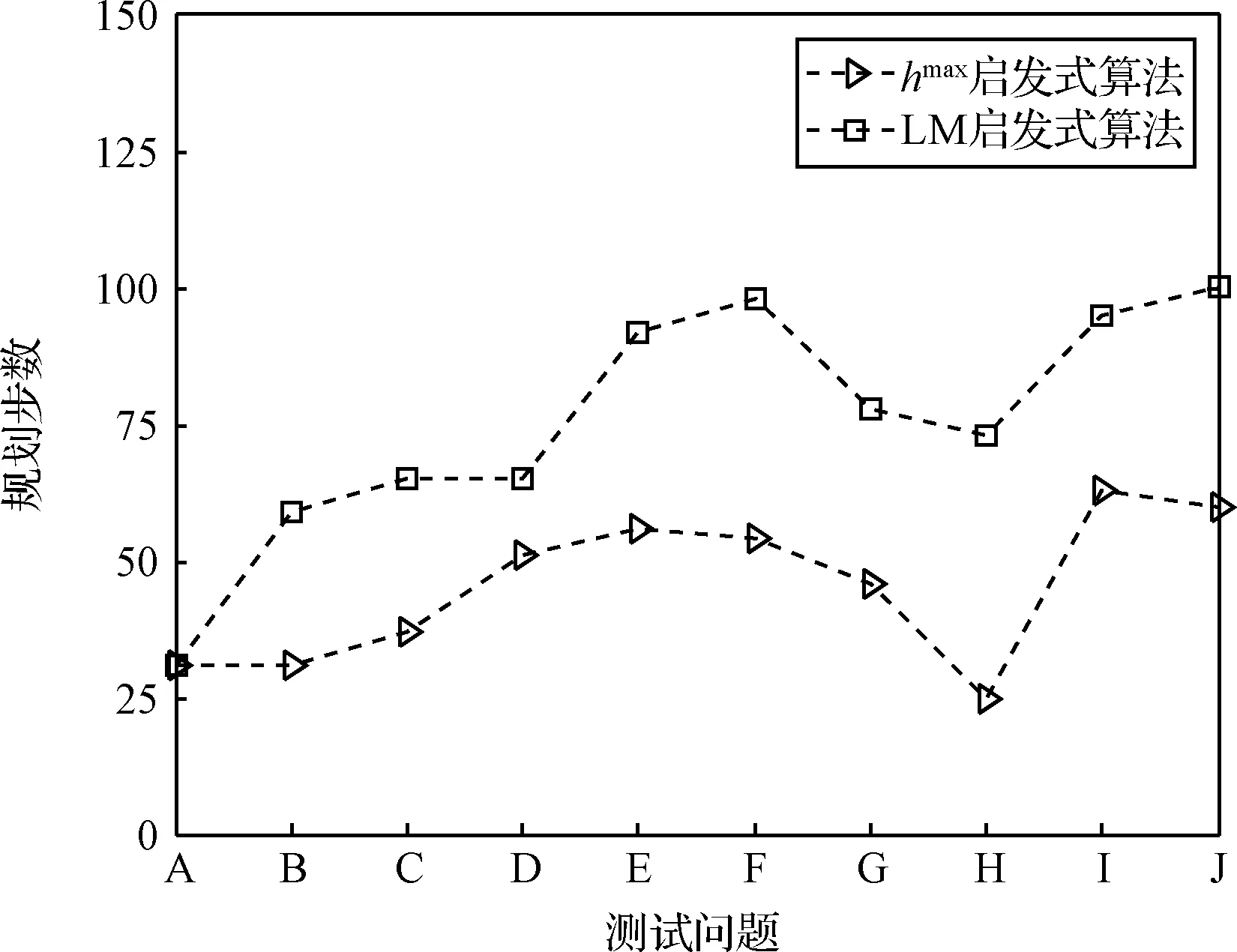
图10 规划步数差对比图

算法的规划步数可根据其是否生成新节点划分为两类：算法迭代过程中存在新节点生成的步骤，称作节点扩展步；不存在新节点生成的步骤，称作非节点扩展步，例如节点回溯。对于同一个规划问题，hmax算法与路标算法所需扩展的节点数量能够直接的反映出其节点评价的准确性。如图11所示，图中每个测试问题对应有两列堆叠柱形，分别表示四部分数据：hmax算法节点扩展步与非节点扩展步同原算法的差值、路标算法节点扩展步与非节点扩展步同原算法的差值。从图中可以清晰地看出，除问题A外，路标算法规划步数的减少量均大于对应问题中hmax算法规划步数的减少量，即路标算法求解各测试问题所需的规划步数均不超过hmax算法所需步数。对于简单问题的规划求解，由于其涉及节点数量较少且搜索空间规模较小，启发式的作用并不明显，故问题A出现两种算法步数完全一致的情况。但随着目标数量的增多，规划求解愈显复杂，算法的每一次迭代都会向搜索空间中加入大量候选规划节点。另外，搜索空间中亦存在大量“死区”节点，即从该节点继续搜索无法得到问题的规划解。因此，启发式评价函数的性能将直接影响规划问题的求解速度。

图11 节点扩展与非节点扩展步数的减少量对比图

如图11所示，在规划步数中，节点扩展步数占有大约一半的比重。即所有减少的规划迭代步数中，有一半及以上的数量来自于节点扩展数目的减少。而节点扩展数目的减少则直接对应于启发式算法的节点评价能力。对于所有测试问题，hmax算法和路标算法均能够保证对原算法的性能提升，而后者的节点扩展数量均不超过前者，故路标算法在节点评价的准确性上更胜一筹。启发式规划算法能够通过节点评价决定节点扩展顺序，直接减少冗余节点的扩展数量；又间接的降低规划陷入“死区”的概率和次数，减少了不必要的回溯步骤。通过两方面的共同作用来提高规划求解的效率。

图12中的曲线展示了两种启发式算法在所有测试问题上相较原算法的规划效率提升。其中路标启发式算法对应曲线的数值大约在40上下变化；而hmax算法在问题A上达到效率提升的峰值，然后逐渐降低，最终回升到30附近。综上，hmax算法和路标算法在所有测试问题上对比原算法均能加速搜索，提高规划效率，且路标算法的性能更好。

5 结论

深空探测器任务规划具有系统复杂、约束耦合且任务多的特点，导致传统规划技术效率低下难以直接应用。针对这一问题，本文提出了一种深空探测器时间线转移路标启发式算法，通过搜索实现任务目标必需的状态集合，减少规划过程中冗余节点扩展数量，实现加速搜索的目的。另外，为了降低启发式计算带来的时间消耗，在不影响路标数量的前提下提出了增量式路标更新方法以及最大目标筛选策略。最后，仿真实验结果表明时间线路标转移启发式算法能够提高规划求解效率，且与时间线hmax规划算法相比计算性能更具优势。