基于复杂网络特性的海运港口地位研究

刘苗苗，蒋艳

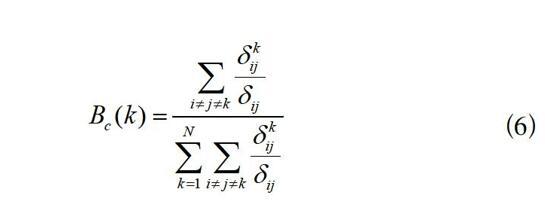
摘  要：随着经济全球化的发展和港口吞吐量的提高，世界海运网络越来越复杂，港口地位的研究也变得愈发重要。本文以港口为节点，以港口间航次连接作为边、航次数量作为权重构建海运复杂网络，并对其特性进行分析;分别计算网络的度中心性、中间中心性、接近中心性，并对三种中心性使用熵权-折中妥协法（EW-VIKOR）多属性决策分析得到折中值，通过折中值对港口中心地位进行排序。根据排序结果可知，排名前四的深圳港、新加坡港、香港港和上海港的折中值差距很小，竞争非常激烈，且都位于海运复杂网络的重要位置，海运复杂网络稳定性依赖于这些港口的穩定发展。本文的创新点在于将加权的复杂网络与EW-VIKOR多属性决策相结合，并将其运用在港口研究中，为港口的经济发展提供更多的参考。

关键词：复杂网络;港口中心性;EW-VIKOR;港口地位;排序

中图分类号：TP183     文献标识码：A

Research on Shipping Ports Status based on Complex Network Characteristics

LIU Miaomiao， JIANG Yan

（Business School， University of Shanghai for Science and Technology， Shanghai 200093， China）

cchloeliu@163.com; ppjyan@163.com

Abstract： With the development of economic globalization and the increase of port throughput， the world's shipping network is becoming more and more complex， and the study of port status has also become important. This paper proposes to use ports as nodes， voyage connections between ports as edges， and voyage quantity as weights to construct a complex shipping network. The characteristics are analyzed， and the degree centrality， the intermediate centrality， and the proximity centrality of the network are calculated separately. The compromise values are obtained by Entropy Weighting-VlseKriterijumska Optimizacija I Kompromisno Resenje （EW-VIKOR） method in multi-attribute decision analysis of three kinds of centrality. Port center status is sorted based on the compromise value. According to the ranking results， top four ports of Shenzhen， Singapore， Hong Kong and Shanghai have very small compromises， and the competition is very fierce. They are all located in important positions in the complex shipping network whose stability depends on the stable development of these ports. The innovation of this paper is to combine the weighted complex network with EW-VIKOR multi-attribute decision-making， and apply it in port research to provide more references for port economic development.

Keywords： complex network; port centrality; EW-VIKOR; port status; ranking

1   引言（Introduction）

目前，对于海运复杂网络的相关研究，关晓光等[1]构造了以航次作为权重的加权网络，对点强度、加权介数和加权接近度进行测量并分析。刘婵娟等[2]构造了“21世纪海上丝绸之路”海运复杂网络，并对拓扑结构复杂性和三种中心性进行分析。陈芙英等[3]使用TOPSIS法对“21世纪海上丝绸之路”沿线港口的地位进行综合评价。伍静等[4]结合伯德计数法提出了一种考虑三种中心性的综合中心性评价方法。JIANG等[5]提出了基于BA规模网络性能理论，提出海上丝绸之路网络节点容量的最优策略。ASADABADI等[6]考虑了港口的可靠性和弹性，以及港口在支持更大的弹性海洋系统中的作用，提出了评估和提高世界海运网络弹性和可靠性的模型。杨忍等[7]使用熵权-层次分析法对海上丝绸之路沿线的重要港口进行综合竞争力评估。陈芙英等[8]应用TOPSIS法对我国具有代表性的18 个沿海港口的竞争力进行综合评价。段雪妍等[9]采用UTAGMS方法并且结合极限排序法和蒙特卡洛仿真法对我国长江干线18 个内河港口竞争力进行实证分析。已有研究中构造复杂网络很少考虑权重，本文构造了航次加权的复杂网络;已有研究中使用的多属性决策方法大多是层次分析法和TOPSIS法，本文使用EW-VIKOR多属性决策方法。

本文基于前七大班轮公司的航线数据和世界排名前五十的港口数据构造了复杂航次加权的世界海运网络，对该海运网络进行拓扑结构复杂性分析和节点中心性多属性目标决策分析，研究港口在世界海运复杂网络中的地位和作用。

本文的创新点在于将加权的复杂网络与EW-VIKOR多属性决策相结合，并将其运用在港口研究中，为港口的经济发展提供更多的参考。

2   复杂海运网络（Complex maritime network）

2.1   数据处理

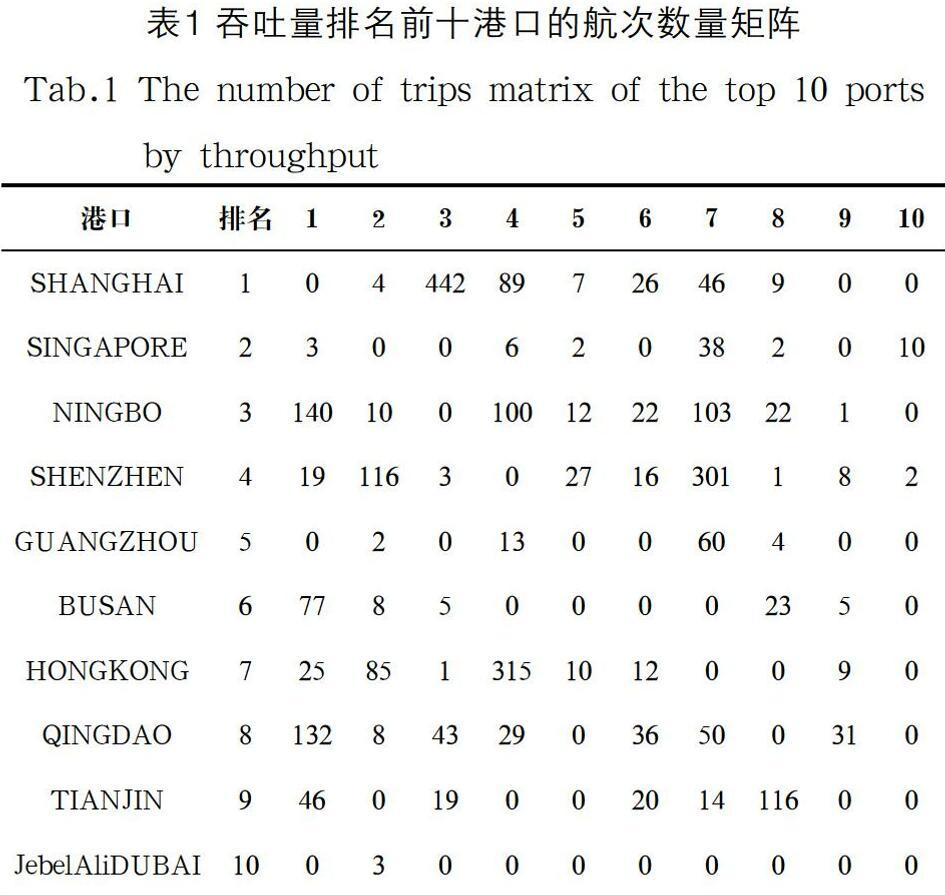
數据来源于中国港口网，根据2019 年港口吞吐量排名，取排名前五十的港口。根据2019 年班轮公司运力排名，取排名前七的班轮公司，其运力都超过了100 万个标准集装箱（TEU）。收集了2020 年4 月—5 月的全部航次信息，包括承运人、起运港、目的港、挂靠港。根据收集的1，267 条航次信息，可以获得船舶在一个航期内经过的港口，以此构建50 个港口的航次数量矩阵。吞吐量排名前十港口的航次数量矩阵如表1所示。

2.2   复杂海运网络构建

将港口作为网络中的节点，两个港口之间存在一条直接相邻的航线的时候作为一条边，港口之间的航次数量作为边上的权重，基于港口和航线之间的关系构造复杂网络;再基于航次数量矩阵，使用netdraw可绘制出海运网络拓扑图，如图1所示。其中，箭头表示班轮运输的航次方向。

从海运网络拓扑图中可以看出，前五十的港口和相关航线构建的复杂海运网络存在复杂的连接关系，港口节点的重要性也不同，由此可见世界所有的港口和各个班轮公司的班轮航线构建的世界海运网络是复杂网络。

3  海运网络复杂性分析（Analysis of shipping network complexity）

为分析世界海运网络的小世界特性，先将整理的航次数量矩阵变为0—1矩阵，再分别计算平均路径长度和聚合系数。

（1）平均路径长度：在网络中，任选两个节点，连通这两个节点的最少边数为两个节点的路径长度，网络中所有节点对的路径长度的平均值为网络的平均路径长度。

设N为港口数量，L为两个港口间距离的平均值，为两个港口所经过的最少边数，则计算公式如式（1）所示。

（1）

使用MATLAB计算平均路径长度为2.1714，说明平均完成2 次中转就可以实现两个港口之间的连接。

（2）聚类系数：假设某个节点有条边，则这条边连接的节点之间最多可能存在的边的条数为（其中k为该节点的度值），用实际存在的边数除以最多可能存在的边数得到的分数值，为这个节点的聚类系数（所有节点的聚合系数的均值为网络的聚类系数）。

设ki是节点i的度值，Ei是与节点i相连的节点之间的连边，则计算公式如式（2）所示。

（2）

使用MATLAB计算得出海运网络的聚类系数为0.5323，说明与一个港口相连的其中两个港口也相连的概率为0.5323。

根据输出的各节点的聚类系数，使用MATLAB做出各港口节点的聚类系数分布直方图，如图2所示。

从港口节点聚类系数分布图中可以看出，50 个港口节点中大多数的节点都具有较高的聚类系数，只有少数节点具有较低的聚类系数，因此，世界海运复杂网络具有较高的聚类系数。

对于规则网络，任意两个点之间的特征路径长度较长，但聚类系数高。对于随机网络，任意两个点之间的特征路径长度短，但聚类系数低。对于小世界网络，点之间特征路径长度短，接近随机网络，而聚类系数依旧相当高，接近规则网络。世界海运复杂网络具有较短的平均路径长度，具有较高的聚类系数，符合网络小世界特性。

4   港口中心性分析（Port centrality analysis）

（1）度中心性

度中心性是指与该节点相连的其他节点的数量，反映了港口节点在海运复杂网络中的地位，其值越大，该港口节点在海运网络中的中心地位越高。

设为节点的度值，为节点个数，则计算公式如式（3）所示。

（3）

根据航次数量矩阵，使用netdraw绘制加权的度中心性的网络拓扑图，如图3所示;使用ucinet 6计算出港口度中心性值绘制柱形图，如图4所示。

度中心性反映的是该港口与其他港口直接连接的数量多少，由图4可以看出，度中心性值排名前三的港口节点4深圳港、港口节点1上海港和港口节点7香港港与其他港口通航较多。

（2）接近中心性

接近中心性衡量的是一个港口节点与其他港口节点的远近程度，该值越小说明该港口是海运网络的核心，反映了该港口不依赖于其他港口进行运输的能力。

设表示港口到港口的最短距离，为港口数量，则计算公式如式（4）、式（5）所示。

（4）

（5）

根据航次数量矩阵，使用netdraw绘制加权的接近中心性的网络拓扑图，如图5所示;使用ucinet 6计算出港口接近中心性值绘制柱形图，如图6所示。

接近中心性反映的是该港口依赖其他港口程度的大小，接近中心性越小说明该港口具有较强的独立性和抗干扰能力，由图6可以看出，接近中心性最小的三个港口分别为港口节点35萨凡纳港、港口节点29马尼拉港和港口节点22纽约和新泽西港，这三个港口是独立性和抗干扰能力较强的港口。

（3）中间中心性

中间中心性用所有节点对之间的最短路径经过给定节点的次数来衡量。在海运复杂网络中，中间中心性衡量的是港口进行海上运输的中转能力，其值越大，中转能力越强。

设表示从港口到港口的加权最短路径的总条数，表示从港口到港口的加权最短路径经过的次数，则计算公式如式（6）所示。

（6）

根据航次数量矩阵，使用netdraw绘制加权的中间中心性的网络拓扑图，如图7所示;使用ucinet 6计算出港口中间中心性值绘制柱形图，如图8所示。

中间中心性反映的是港口在海运复杂网络中的中转能力，由图8可以看出，中间中心性排名前三的是港口节点2新加坡港、港口节点4深圳港和港口节点15高雄港，这三个港口具有较强的中转能力。

5  考虑中心性的港口地位排序（Port status ranking with consideration of the centrality）

根据航次数量矩阵，使用ucinet 6计算出集装箱吞吐量排名前五十的港口各中心性值，如表2所示。

从上面的分析中可以看出：度中心性数值大的港口，中间中心性数值和接近中心性数值不一定也较大，即与其他港口通航数量较多的港口，不一定具有较强的中转能力，也不一定具有较强的独立性和抗干扰能力，因此需要对三种中心性进行综合评价来确定港口的中心地位。本文使用熵权-折中妥协法（EW-VIKOR）对港口的中心地位进行排序。

5.1   用熵权法确定权重

用熵权法确定权重的步骤如下：

（1）数据标准化

将数据进行标准化，每个中心性指标进行标准化的公式如式（7）所示。

（7）

（2）求各中心性指标的信息熵

每组数据的信息熵计算公式如式（8）所示。

（8）

其中，，如果，则。

（3）确定各中心性指标的权重

各中心性指标权重的计算公式如式（9）所示。

（9）

根据规范化后的数据计算出各中心性指标的权重，如表3所示，其中，是度中心性指标权重，是中間中心性指标权重，是接近中心性指标权重。

将海运复杂网络中心性指标进行标准化处理，各指标的量纲不同，且又有效益型指标：度中心性和中间中心性;还有成本型指标：接近中心性。将各指标标准化处理，，加权化后排名前五十港口的各中心性值如表4所示。

5.2   用VIKOR法进行综合中心性排序

将50 个港口看作50 个决策方案，三种中心性指标看作三个决策属性，对海运复杂网络港口中心地位进行多属性决策排序。

（1）确定三个中心性的最优值与最劣值，，如式（10）、式（11）所示。

（10）

（11）

（2）确定加权规范化，如式（12）所示。

（12）

（3）确定加权规范化找到的所有决策方案的群体效益值和个别遗憾度，，如式（13）、式（14）所示。

（13）

（14）

其中，越大，群体效益值越大;越小，个别遗憾度越小。

（4）计算所有港口的折中值，如式（15）所示。

（15）

其中，是决策机制系数，表示根据大多数决议的方式制定决策;表示根据拒绝情况制定决策;近似0.5表示根据同时追求群体效益最大和个别遗憾度最小制定决策。因此，取。

（5）根据折中值对港口进行排序，结果如表5所示。

排名前四的港口折中值差距很小，排名第一的是深圳港，排名第二的是新加坡港，排名第三的是香港港，排名第四的是上海港。折中值排名前十的港口中我国占了六个，说明我国在世界海运集装箱网络中的地位远远高于其他国家，占据海运网络的中心位置。但是亚洲各港口间竞争也比较激烈，新加坡港是世界海运网络最大的中转中心，使其综合中心性的位置排在第二。因此，随着海运网络的不断发展，我国还需要不断提高港口竞争力以加强在世界海运网络中的地位。

6   结论（Conclusion）

以港口为节点，以港口间航次连接作为边、航次数量作为权重构建海运复杂网络。对海运复杂网络进行分析，分别计算网络的度中心性、中间中心性、接近中心性，将三种中心性作为决策属性，港口作为决策方案。熵权-折中妥协法是一种主观和客观相结合的多属性决策方法，使用此方法对港口的中心地位进行排序，能够合理地反映出海运网络中各港口的中心地位，为港口的发展和政策的制定提供科学的依据。

根据排序结果可以看出各个港口的差异较大，排名前四的深圳港、新加坡港、香港港和上海港的折中值差距很小，竞争非常激烈，且都位于海运复杂网络的重要位置，海运复杂网络稳定性依赖于这些港口的稳定发展。使用将加权的复杂网络与EW-VIKOR多属性决策相结合的方法研究港口的中心地位，此方法为全球贸易发展中港口的建设提供了更多的参考。

参考文献（References）

[1] 关晓光，李振福，陈雪，等.基于航次加权的世界集装箱港口复杂网络结构及港口中心性研究[J/OL].大连海事大学学报，2020，46（03）：11-21.

[2] 刘婵娟，胡志华.“21世纪海上丝绸之路”海运网络空间格局及其复杂性研究[J].世界地理研究，2018，27（03）：11-18.

[3] 陈芙英，张建同，罗梅丰.“21世纪海上丝绸之路”沿线港口地位综合评价[J].运筹与管理，2020，29（01）：157-164.

[4] 伍静，张笛，万程鹏.基于复杂网络的海上丝绸之路沿线港口地位评价[J].交通信息与安全，2019，37（03）：101-108.

[5] JIANG L P， JIA Y， ZHANG C， et al. Analysis of topology and routing strategy of container shipping network on "Maritime Silk Road"[J]. Informatics and Systems， 2019（21）：72-79.

[6] ASADABADI A， MILLER-HOOKS E. Maritime port network resiliency and reliability through co-opetition[J]. Logistics and Transportation Review， 2020（137）：1-17.

[7] 杨忍，牟乃夏，彭澎，等.“海上丝绸之路”沿线重要港口竞争力评价[J].地球信息科学学报，2018，20（05）：623-631.

[8] 陈芙英，张建同.“一带一路”倡议下我国沿海港口竞争力评价与比较研究[J/OL].工业工程与管理，2021，26（03）：1-7.

[9] 段雪妍，余思勤，王效俐，等.基于UTAGMS方法的内河港口竞争力排序[J].上海海事大学学报，2015，36（01）：6-11.

作者简介：

刘苗苗（1993-），女，硕士生.研究领域：决策分析.

蒋   艳（1974-），女，博士，副教授.研究领域：多目标决策.