柱面SH波作用下管道的动应力集中研究

路世伟，孙金山，刘洪宇，周传波

(1.长江大学城市建设学院，湖北 荆州 434023；2.江汉大学湖北(武汉)爆炸与爆破技术研究院，武汉 430056； 3.中国地质大学(武汉)工程学院，武汉 430074)

在过去的几十年，随着地下空间的大力开发，越来越多的地下工程采用钻爆法开挖。爆破地震波对临近管道的安全产生了显著的影响，深入分析管道在爆破地震波作用下的动力响应特性具有重要的理论和实用价值。

Pao等[1-2]对地下结构在平面波作用下的响应进行了广泛的研究，从理论上研究了无界弹性介质中圆形孔洞和衬砌隧道在平面波作用下的动应力集中系数(DSCF)。Lee等[3-4]基于Fourier-Bessel展开和多极坐标研究了不同深度的圆柱腔对平面P波和SV波的散射和衍射。Wang[5]，Liu等[6-7]研究了半饱和空间中管道对弹性波的散射。王晓炜[8]对取水隧洞内外爆破振动进行了安全分析。Smerzini等[9]研究了SH波入射时地下洞室对地面运动的影响。Lin等[10]研究了平面纵波作用下平面弹性半空间圆形地下隧道的动力响应。付佳等[11]研究了平面SH波作用下土-隧道相互作用。Xu[12]在莫尔-库仑准则的基础上，研究了以鲁新煤矿为背景的单线环形隧道爆破振动安全判据。

在过去，爆破地震波一般被视为平面波，适用于震源较远的情况。然而，钻爆法有时必须在现有地下结构附近进行。平面波的假设已不再适用，必须考虑波前的曲率。因此一些研究者开始研究圆柱波的传播。Yi等[13]研究了柱型纵波作用下圆形衬砌隧道的动应力集中。Lu等[14-15]研究了柱面P波作用下圆形无衬砌隧道的动应力集中和振动速度分布。到目前为止，关于柱面SH波对地下结构动力响应的理论研究还很少。

笔者选择爆破地震波中的柱面SH波作为研究对象，基于Fourier-Bessel展开推导了柱面SH波作用下管道内壁上动应力集中系数的解析解。以宝通禅寺地下通道爆破开挖为例，讨论了爆心距和入射波频率对DSCF的影响。最后，给出了波阵面曲率的影响可以忽略的爆心距阈值。

1 管道与土体的动力相互作用分析

1.1 简化模型

我们假设一个线状波源位于O1，圆形管道轴线与O2重合，内半径为a，外半径为b，O1O2之间的距离为r0，并在O1与O2分别建立坐标系O1x1y1与O2x2y2(见图1)。P为土体中任意一点，与O1、O2的距离分别为r1、r2，在O1处产生的柱面SH波的位移函数为[16-17]

(1)

图1 柱面SH波Fig.1 Cylindrical SH-wave

通常，当圆柱形SH波到达管道时，会在土壤中产生向外传播的反射SH波(W(r))，在管道中产生向外和向内传播的折射SH波(W(f))。它们的位移可以表示成如下形式：

Ensinnθ2]exp(-iωt)

(2)

Gnsinnθ2]exp(-iωt)

(3)

为求入射波、反射波、折射波叠加后的位移函数，我们必须将O1x1y1坐标系中的入射波势函数转换到O2x2y2坐标系下的表达形式，转换公式如下[13-14]：

(4)

将公式(4)代入公式(1)可得：

(5)

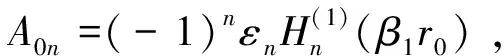
1.2 边界条件

令W1=W(i)+W(r)和W2=W(f)，考虑管道与土体之间的接触面模型为理想接触，那么边界条件可以表示成如下形式：

(6)

柱面SH波的位移和应力具有如下关系：

(7)

代入式(6)中即可求得Bn、Cn、Dn、En、Fn、Gn的结果。

2 工程试验

宝通禅寺地下通道近距离下穿混凝土污水管，采用钻爆法开挖，通道顶部距离污水管最近距离只有0.69 m，管道材料密度2 400 kg/m3，剪切模量12.61 GPa，内半径a为400 mm，外半径b为465 mm，周围土层密度为1 980 kg/m3，剪切模量为150 MPa。通过相关研究可知，爆破地震波主频为200 Hz以下。故本文选择f=10～200 Hz，r0=(3～10)b来分析SH波入射情况下管道动力响应特性。

为方便分析和得到一般性的结论，本文定义动应力集中系数DSCF和归一化爆心距r*如下：

(9)

r*=r0/b

(10)

2.1 收敛性分析

由于解析解为无穷级数，级数截断项数会直接影响计算结果的精确性。本文选择入射波频率为10 Hz和200 Hz，r*=3两种情况进行收敛性分析，不同截断项数时动应力集中系数DSCF分布结果如图2所示。

图2 不同截断项数时DSCF随角度θ2变化Fig.2 Variation of DSCF with θ2 under different number of truncated terms

由图2可知，DSCF随着项数的增加迅速收敛，当项数超过10项时，DSCF的变化基本可以忽略不计。为保证更广范围内的计算精度，本文选择截断项数为20项。

2.2 入射波频率和爆心距的影响

为研究入射波频率f和归一化爆心距r*对动应力集中系数分布情况，分别绘制了f为10、50、100、200 Hz时动应力集中系数分布曲线(见图3)。

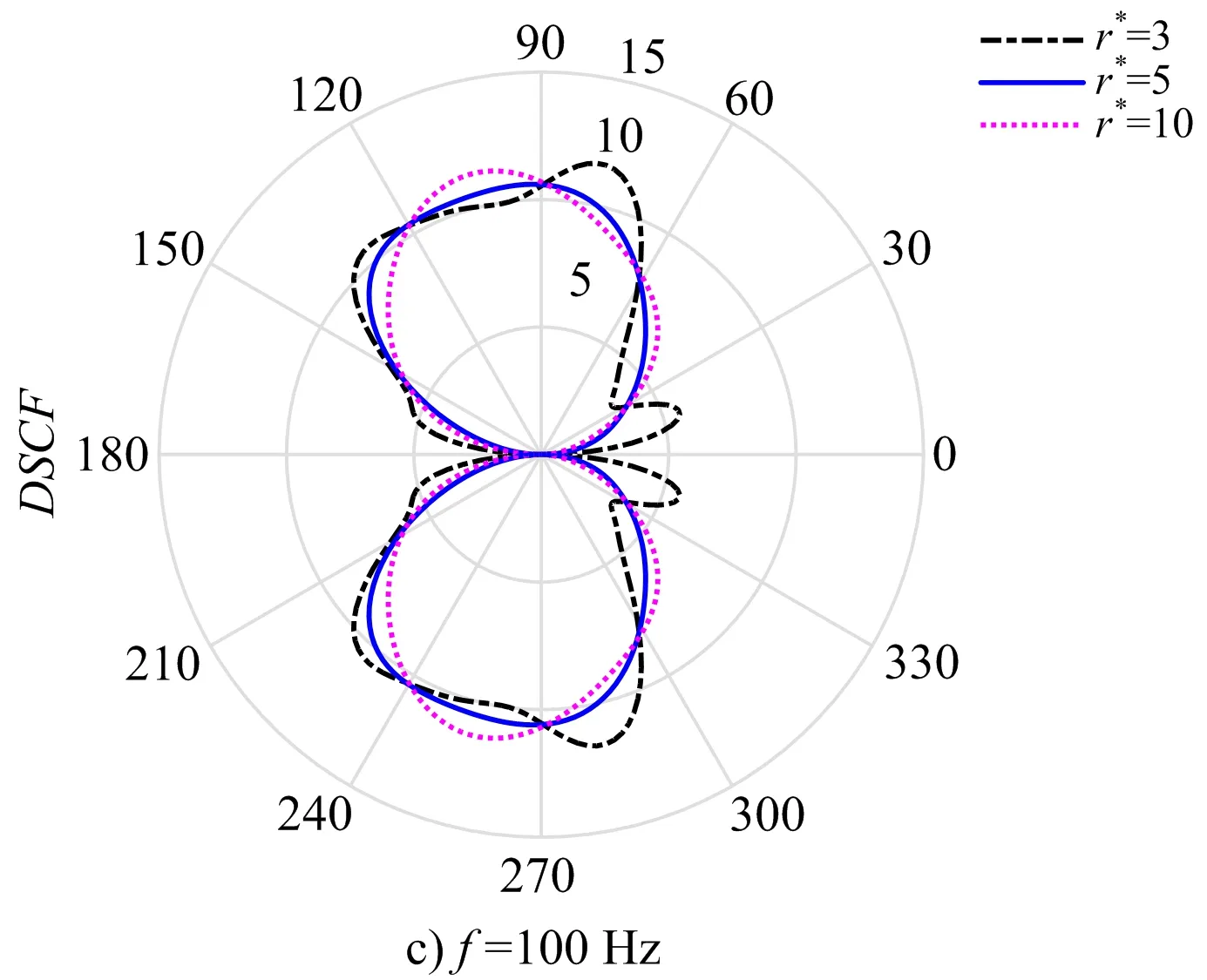
图3 DSCF分布Fig.3 Distribution of DSCF

由图3可知，由于管道与周围土层剪切模量差异较大，管道上的动应力集中系数普遍较大，这说明管道剪切模量越大，管道承受的动应力也越大。当f=10、50、100 Hz时，DSCF在迎爆侧和背爆侧均出现了较大值，而当f=200 Hz时，DSCF主要在迎爆侧出现了较大值，这表明随着入射波频率的增加，入射波的绕射能力减小，其携带的能量被迎爆侧反射的越多。当f=10、50 Hz时，DSCF最大值随r*的增大而迅速减小，当r*>5时DSCF最大值趋于稳定；当f=100、200 Hz时，DSCF最大值随r*的增大基本不发生变化。这表明从动应力集中系数DSCF分布的角度来讲，当r*<5时，柱面波与平面波的差异较大，但当r*>5时柱面SH波基本可以认为与平面SH波等价。

为更详尽地了解DSCF最大值与归一化爆心距r*和入射波频率f之间的关系，绘制了不同频段DSCF最大值的分布图(见图4)。

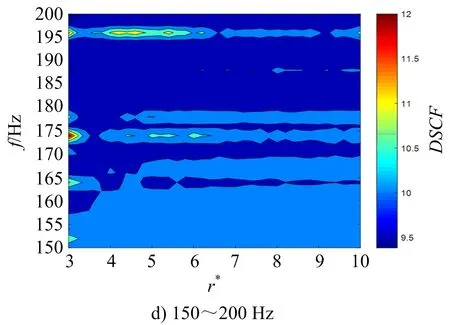
图4 不同频段时DSCF最大值分布Fig.4 Distribution of maximum DSCF in different frequency range

由图4可知，当r*=3时，DSCF在16、48 Hz时出现了非常大的峰值，这说明16、48 Hz接近管道的前2阶自振频率。当入射波频率较低(10～100 Hz)时，DSCF最大值随r*的增大迅速减小，变化趋势较为明显，而当入射波频率较高(100～200 Hz)时，DSCF最大值随r*的变化趋势并不明显，这也表明低频入射波对管道的安全更为显著，特别是入射波频率与管道自振频率接近时，管道受到的影响最为严重。

3 结论

1)基于波函数展开法推导了柱面SH波与管道相互作用时动应力集中系数的表达式。

2)由于管道与周围土层剪切模量差异较大，管道上的动应力集中系数普遍较大。

3)从动应力集中系数DSCF分布的角度来讲，当归一化爆心距r*<5时，柱面波与平面波的差异较大，但当r*>5时,柱面SH波可以认为与平面SH波等价。

4)低频入射波对管道的安全更为显著，特别是入射波频率与管道自振频率接近时，管道受到的影响最为严重。