基于时频矩阵相似度的配电网单相接地故障选线
王 芳
(三峡大学电气与新能源学院,湖北 宜昌 443002)
中性点不直接接地即小电流接地系统为我国中低压配电网广泛采用的中性点接地方式。采用这种中性点接地方式的配电系统的供电可靠性比较符合现阶段配电系统的发展需求。配电网发生单相接地故障后一般保持系统原有运行方式继续工作1~2 h,这符合城市配电网对供电可靠性的要求,且随着电缆线路的增多,城市配电网采用中性点经消弧线圈的谐振接地方式有利于实现这一要求。但是,谐振接地系统在发生单相接地故障时如果长时间带故障运行必将发生连锁故障甚至发生弧光过电压,这将导致多相短路造成线路跳闸,这对于对停电时户数要求较高的城市配电系统是不允许发生的。为此,在单相接地故障发生的初期及时地排查故障线路后予以切除显得尤为重要[1]。
然而,由于谐振接地系统的故障特征,故障点电流被补偿为极小的感性电流,这给故障选线保护造成极大的困难。常规继电保护装置基于稳态相量模型很难进行故障选线,因此,对于谐振接地系统的单相接地故障必须采用特定的继电保护选线装置。最初人们采用的是手动拉闸的方法,显然这种方法同配电自动化的要求格格不入,为了解决小电流接地故障选线的难题,学者们进行了大量的研究。
目前常见的小电流故障选线方法大致分为两类,一种为主动注入法[2-3],主动注入法要通过额外的装置实现选线功能,由于增加了额外的装置使得其成本大大增高;另一种则为被动检测法,被动按照信号类型可以分为稳态法[4-6]与暂态法2种。从经济性和可靠性两方面考虑现多采用被动检测法。其中又以暂态分析法最为常用,因为暂态分析法采用先进的信号分析算法,选线准确率较高。文献[7-8]将小波分析法分引入到小电流故障选线中,采用小波函数的伸缩变换实现对输入信号的多频带分析,该方法原理简单且计算量小,但是该方法容易出现模态混叠现象,影响选线的准确性。随着EMD算法[9-12]的提出和广泛应用,该算法及其各种改进算法可以明显减少模态混叠的发生,但存在分解后信息不直观的问题。为了进一步解决该问题,文献[13]基于Prony算法分析配电线路的零序电流分量,继而实现小电流接地系统故障选线,Prony算法虽然可以改善分解信息不够直观的问题但是该算法稳定性极易受高频噪声的影响;于是大量学者提出利用混沌振子[14]以及S变换[15]等方法来实现故障选线。但是此类算法存在分解后信息量较大且不易被利用的问题。
为此,文中采用Hilbert-Huang变换和时频矩阵相似度对谐振接地系统故障选线,并提出了一种经Hilbert-Huang变换后零序电流的时频矩阵相似度故障选线的判据。由于加权Hausdorff距离分析的是暂态零序电流波形总体上的波形相似度,故取故障后1/4个周波时间窗口内零序电流离散采样值进行暂态分析,通过仿真结果分析验证了文中所提出的选线算法具有较好的正确率和鲁棒性。
1 谐振接地系统故障特征
如图1所示为含有2条出线和1条母线的谐振接地系统,该系统的出线L2发生单相接地故障后系统故障线路和健全线路零序电流流向分别采用不同箭头符号予以表示。此时,系统各相对地电压及中性点对地电压的情况与中性点不接地配网相同。在图1中,消弧线圈L的作用是通过采用感性电流对线路对地电容电流进行补偿,即相对于故障电流中叠加一个与其方向相反的感性电流,从而使得故障电流减小甚至由容性变为感性分量。

图1 谐振接地系统单相故障示意图
(1)
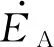
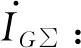
(2)
式中:C∑为各元件对地电容的总和;L为消弧线圈的电感值;ω为工频角频率。
在谐振接地系统发生单相接地故障时,根据各出线零序电流的方向识别故障线路的方法难以奏效,但是故障线路和健全线路中暂态零序电流分量含有丰富的故障信号,并且二者的暂态零序电流的幅值和方向均不相同,其波形中的振荡分量的大小差异也十分明显[16]。为此,文中考虑采用HHT建立线路零序电流时间序列的时频矩阵,并依据时频矩阵相似度作为选线的依据。
2 Hilbert-Huang变换及时频矩阵的建立
Hilbert-Huang变换(HHT)包括2种基本计算方法,即经验模态分解(EMD)计算和Hilbert变换(HT)计算。具体地,HHT首先将原始信号进行EMD计算后得到需要数目的本征模态函数后,再采用Hilbert变换计算本征模态函数的瞬时频率谱、瞬时幅值谱以及Hilbert时频谱与Hilbert边际谱。
经验模态分解 (empirical mode decomposition,EMD) 认为任何信号都可分解成具有不同固有振动模态函数的集合。其核心操作是将任意的信号分解为不同频率尺度上的本征模态函数(intrinsic mode function,IMF)和一个残差函数,即原始时间序列s(t)可以表示为n个不同尺度的本征模态函数ci和残差项r(t)的和,即为
(3)
在EMD分解的基础上,对任意的本征模态函数ci(t)进行Hilbert变换后的信号函数为
(4)
再对变换后的信号量进行反Hilbert变换后得到:
(5)
根据式(4)和式(5)得到本征模态函数的解析信号量,该信号以ci(t)为实部,ui(t)为虚部构成如下的复合信号:
xi(t)=ci(t)+j·ui(t)=ai(t)ejθi(t)
(6)
式中:ai(t)为解析信号的瞬时幅值;θi(t)为解析信号的瞬时相位。对瞬时相位求一阶导数继而可得瞬时角频率ωi(t)以及瞬时频率fi(t),相应的计算公式如下:
(7)
(8)
(9)
经过HHT后,原始信号s(t)可以表示为下式:
(10)
采用全部的本征模态函数分量的瞬时幅值和瞬时频率即可得到Hilbert时频谱,由Hilbert时频谱可以构造出二维时频矩阵H:
(11)
式(11)中,将瞬时频率归一化为区间[0,0.5]上的值,原始数据长度为M,去掉首末时间端点后HHT变换后的数据长度为N=M-2,符号[ ]代表取整函数。
m=[j(N-1)/N]+1
n=[2fij(N-1)]+1
Hmm=Hmm+aij,i,j∈(1,N)
(12)
3 时频矩阵特征提取及矩阵相似度计算
3.1 奇异值分解及特征提取
奇异值分解(singular value decomposition , SVD)对于高维矩阵来说是一种非常有效的处理工具,其本质是矩阵在酉相似条件下的一种标准型,相较与其他的矩阵相似标准型而言,酉相似标准型可以保留原矩阵的更多特性,并可以适度地剔除一些无关轻重的影响因子。换言之,奇异值分解可以捕捉矩阵的结构信息,并有效地提取关键特征因子,剔除矩阵冗余因子。
对于实矩阵A∈Rm×n,那么存在正交矩阵U∈Rm×m和V∈Rn×n,使得:
(13)
式中:正交矩阵U=[u1,u2,…,um]的列向量为单位向量且相互正交,其是矩阵AAT的特征向量,被称为左奇异值向量;正交矩阵V=[v1,v2,…,vn]的列向量也是单位正交向量,同时也是矩阵AT-A的特征向量,被称为右奇异值向量。∑1是矩阵A的非零奇异值按降序排列的格式构成的对角矩阵,即∑1=diag(λ1),i∈(1,p)其中p=min(m,n)。对于本文由HHT得到图2中的零序电流的时频矩阵进行SVD分解后发现,只有大致前20个奇异值是非零且较大外,后面的奇异值都已经十分接近于零且较小。因此,取前p=20个奇异值对应的左右奇异值向量进行矩阵相似度计算。
3.2 基于加权Hausdorff距离的矩阵相似度计算
针对2条曲线的相似度匹配计算的问题,目前主要有两类计算方法即图形灰度信息类算法和图形特征点类算法,其中图形特征点类算法的典型代表有Hausdorff距离算法和Frechet距离算法。其中,Hausdorff距离算法采用的是测度待识别点集和已知点集之间的最大最小距离。已知样本点集S=[s11,s12,…,s1m]和测试点集T=[t21,t22,…,t2n],二者之间Hausdorff距离的公式如下:
D(S,T)=max[d(S,T),d(T,S)]
(14)
式(14)中,d(S,T)表示点集S到点集T的单向Hausdorff距离,即:
(15)
根据式(14)计算出点集S到点集T之间的Hausdorff距离D(S,T)。显然,Hausdorff距离值越小表明点集S和T之间的相似程度越高。
为了反映零序电流的时频矩阵的不同奇异值大小对时频矩阵结构的影响是不同的,采用改进的加权Hausdorff距离值d,即:
(16)
式(16)中,δ1和δ2分别表示样本时频矩阵A1和待测时频矩阵A2的前p个奇异值的累加和,即:
(17)
4 基于时频矩阵相似度的小电流故障选线算法有效性验证
如图2所示,采用Matlab/Simulink仿真软件建立10 kV配电网小电流谐振接地系统发生单相接地故障时的简化仿真模型。该仿真模型含有1台220 kV/10 kV 的降压变压器T,220 kV交流网侧母线采用三相理想电压源模型,4条馈线从下到上依次编号为L1-L4。消弧线圈采用电感L0和电阻R0组成的串联模型,Rg为馈电架空线路或电缆发生接地故障时的过渡电阻。在10 kV配电网系统中,馈线通常是架空线路和电缆线路的混合出线。为此,在仿真模型中架空线路和电缆线路采用集中参数级联等值电路模型,L1、L2、L3均为架空线路,L4为电缆线路,其输电线路长度分别为7 km、15 km、25 km和12 km。消弧线圈工作在过补偿状态,且R0=30 Ω、L0=0.87 H。故障起始时刻设置为0.04 s。
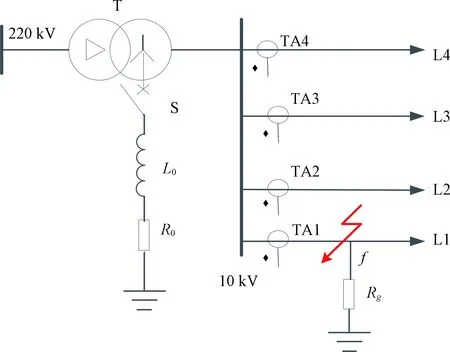
图2 小电流接地系统简化模型
实际中计算每条馈线零序电流是采用软件来计算的,其计算的硬件基础是每条馈线上安装的电流互感器TA的极性接线均正确。由于三相四线制交流电源的零线上流过的是三相负载的不平衡电流,已知三相负载电流时其工频零序电流相量的计算公式为
(18)
但在实际馈线发生单相接地时,各种频率的零序电流分量都有,采用工频零序电流相量已经不能满足快速选线的要求,为此实际中考虑到选线的准确性,一般采用工频分量加特定频率段内的零序电流作为样本零序电流构成选线判据,即:
ins(k)=igs(k)+izs(k),k=1,2,…,M
(19)
小电流单相接地故障微机保护按照20 kHz的频率采样获取线路零序电流离散值,提取工频电流分量采用的是傅里叶算法获取工频相量,特定频率段内的零序电流采用小波变换获得。相关研究表明,故障过渡电阻、故障初始时刻电源电压的初相位依据故障点距离母线的距离是影响线路暂态零序电流分量大小的主要因素。为此,文中为保证采用不同馈线零序电流时频矩阵相似度进行配电网选线的准确性,将在不同的过渡电阻、故障电压初相角和故障位置等工况的故障状态进行仿真分析。
4.1 故障接地电阻值对选线效果的影响
本节主要是验证不同的接地电阻对于采用时频矩阵相似度进行故障线路辨别的影响程度。为此,在故障点f处分别设置接地电阻Rg为0 Ω、30 Ω、50 Ω、100 Ω和300 Ω,保持故障初始时刻电源电压的初相角φ=10°不变,设置故障点到馈线L1母线侧的距离为5 km。经Simulink平台仿真得到各条出线的电流采样值后经离散傅里叶算法和小波变换后的得到待比较的零序电流序列值,从而计算接地故障后L1-L4之间的零序电流时频矩阵相似度。将2条不同编号的出线不同组合分别记为 (L1,L2)、 (L1,L3)、(L1,L4)、(L2,L3)、(L2,L4)、(L3,L4),选线组别依次记为{1,2,3,4,5,6},依次比较每条出线之间的零序电流构成的时频矩阵相似度,得到相应的判别图像,从而筛选出故障线路。
从图3中观察不同线路之间的时频矩阵相似度,可以发现健全线路L2-L4之间的零序电流时频矩阵相似度在[0.47,0.62]之间,数值波动较小;而故障线路L1与健全线路L2-L4之间的零序电流时频矩阵相似度大于1.37,随着接地电阻的增加,它们之间的零序电流时频矩阵相似度呈现增大的趋势,这说明本文的算法有一定的耐过渡电阻的能力。当接地电阻增大时,零序电流的数值也相应地减小,选线变得更加困难,从而可以说明本文选线算法的有效性。
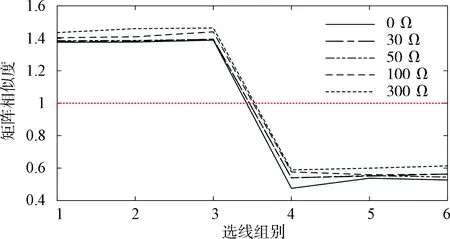
图3 不同接地电阻下线路间的时频矩阵相似度
4.2 电压初相角对故障选线的影响
本节主要是验证不同的电压初相角对于采用时频矩阵相似度进行故障线路辨别的影响程度。分别设置不同的故障电压初相角为 0°、30°、60°和90°,过渡电阻Rg=100 Ω,线路L1短路距离设置为距离母线1 km处,仿真并计算接地故障后L1-L4之间的零序电流时频矩阵相似度。将2条不同编号的出线不同组合分别记为 (L1,L2)、 (L1,L3)、 (L1,L4)、(L2,L3)、(L2,L4)、(L3,L4),选线组别依次记为{1,2,3,4,5,6},依次比较每条出线之间的零序电流构成的时频矩阵相似度,得到相应的判别图像,从而筛选出故障线路。
从图4中可以看出,在不同的故障电压初相角下,当初相角为0°时,故障线路和健全线路的零序电流时频矩阵的零序电流时频矩阵相似度最大,大致落在区间[1.41, 1.46]内,而健全线路的零序电流波形最为相似。随着故障电压初相角的增加,故障线路和健全线路之间的零序电流时频矩阵相似度会有一定下降,但是两者之间的零序电流时频矩阵相似度依然大于1.3,而健全线路之间的零序电流时频矩阵相似度始终小于0.6。从中可以看出其明显和健全线路之间的零序电流时频矩阵相似度不同,从而可以保证故障选线的正确性。

图4 不同故障电压初相角下线路间的时频矩阵相似度
4.3 不同短路距离下的故障选线验证
本节主要是验证不同短路距离对于采用时频矩阵相似度进行故障线路辨别的影响程度。分别设置不同的故障短路距离为1 km、3 km、5 km和6 km,接地电阻Rg=100 Ω,故障电压初相角φ=10°,仿真并计算接地故障后L1-L4之间的零序电流时频矩阵相似度。将2条不同编号的出线不同组合分别记为 (L1,L2)、(L1,L3)、 (L1,L4)、(L2,L3)、(L2,L4)、(L3,L4),相应选线组别依次记为{1,2,3,4,5,6},依次比较每条出线之间的零序电流构成的时频矩阵相似度,得到相应的判别图像,从而筛选出故障线路。
在图5中,在不同故障点距离母线距离下,故障选线的准确性依旧得到保证,这说明加权Hausdorff距离不受短路距离的影响。上述在不同内外因素的干扰下,选线结果验证了所提算法的有效性和抗干扰能力。
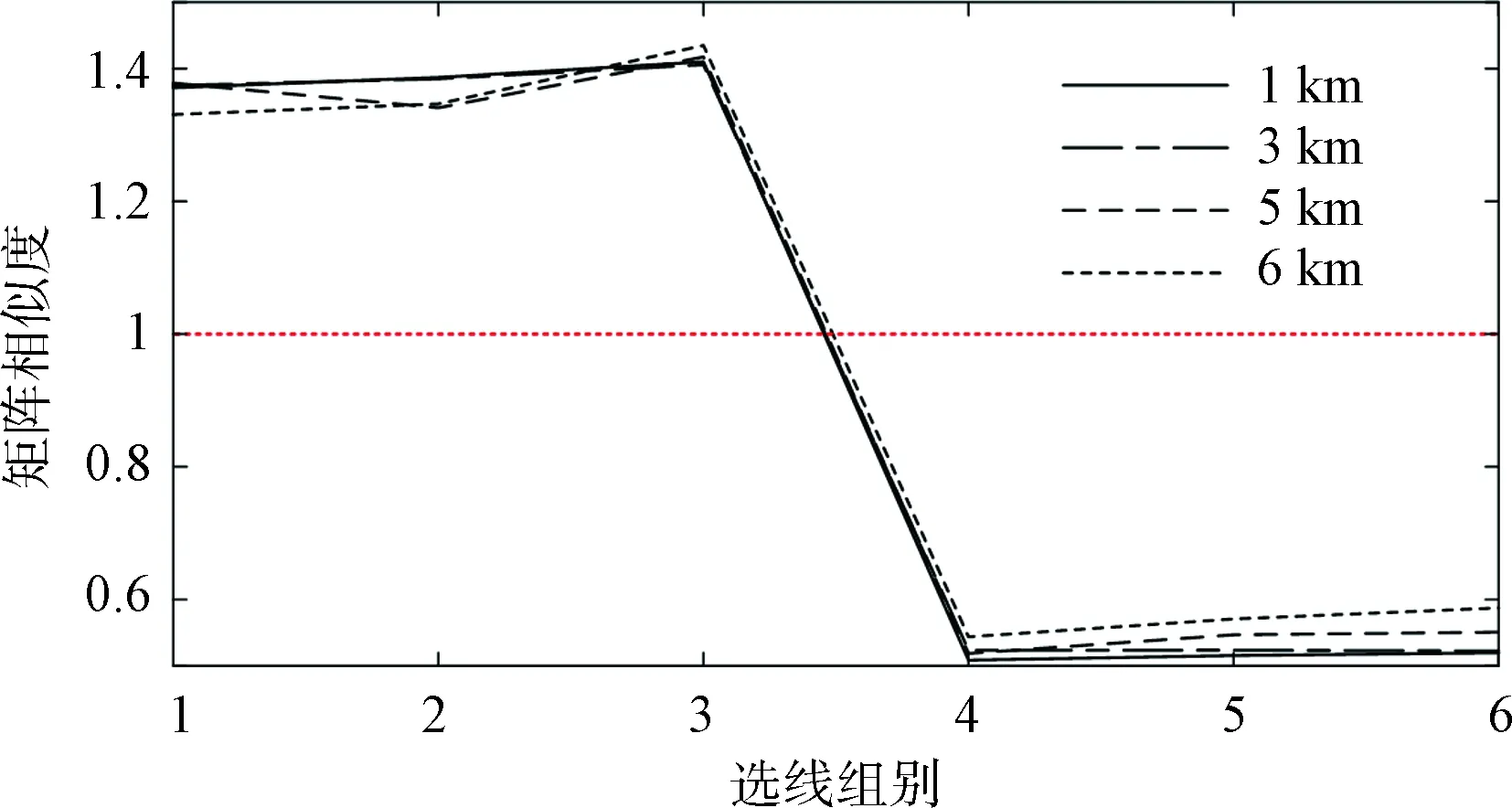
图5 不同短路距离下线路间的时频矩阵相似度
5 结束语
利用Hilbert-Huang变换和时频矩阵相似度实现了对谐振接地系统故障线路的选线方案设计。首先,求取在HHT变换后的各线路零序电流间的时频矩阵的零序电流时频矩阵相似度,并以此作为判据进行故障选线。在不同配电网故障条件下,对所提的选线算法分别进行建模仿真,并计算出相应的零序电流时频矩阵相似度大小,仿真结果可以满足故障选线的要求。这表明基于HHT和时频矩阵相似度的选线算法在不同过渡电阻、合闸初相角、故障距离等外界干扰因素下,依然具有较好的选线准确率和鲁棒性。

