±1100 kV特高压直流导线表面标称电场及其影响因素研究
李星举
(国网鞍山供电公司,辽宁 鞍山 114200)
特高压直流(UHVDC)输电技术是我国西电东送战略的核心技术。当前我国特高压直流输电的电压等级为±800 kV和±1100 kV。我国±1100 kV特高压直流输电工程已经进入设计和建设阶段。近年来,特高压直流输电导线表面的电晕放电所引起的电磁环境现象逐渐受到学者的重视[1-4]。当特高压直流输电导线的表面电场强度超过电晕放电的临界场强时,特高压输电导线周围的空气分子将被电离,成为正负离子[5-6],产生空间电荷[7-8]。在高压导线和地面之间的电场作用下,离子和空间电荷发生定向运动,形成离子电流[9-10]。特高压输电导线和大地之间的Laplace电场与空间电荷或离子的Poisson电场共同作用,形成合成电场[11-13],又称为离子流场[14-16]。
由于导线表面电场强度与诸如无线电干扰(RI)[17-18]、可听噪声(AN)[19-20]、地面处的合成电场和离子流密度等电磁环境参数密切相关,因而有必要计算并控制特高压输电导线的表面电场强度。计算UHVDC导线表面或地面处的电场即合成电场,有经验公式法[21]、模拟电荷法[22-23]、有限差分法[16]和有限元法[1,11,15,24-25]等。每种方法都有其优点和缺点。经验公式法算法最简单,但其精度较差。加拿大多伦多大学的Maruvada与Janischewskyj提出了基于Deustch假设的通量线法,计算单极线路的电晕损失[26],并将该方法扩展到了双极输电导线结构的情况[27]。通量线与电场线在单一介质空间内是重合的。在Laplace电场中确定每条电通量线的位置,再通过迭代方法计算导线表面的电荷密度,再通过沿电通量线递推即可获得整条电通量线上的电荷密度值和场强值。
有限差分法适用于电极结构较为规则的场域,±1100 kV使用双极8分裂导线结构[28],导线处的剖分可能需要线性插值[23]。有限元法适用于结构复杂的场域;但根据电磁场原理,使用一阶线性单元时,由于单元内场强为一个常数,单元之间的场强可能是不连续的,使得电极表面即高压导线表面的场强计算出现误差。使用高阶单元[29-30]或边界电场约束方程[31]可以解决这一问题。
本文使用模拟电荷法计算±1100 kV特高压直流输电子导线表面的标称电场分布,将高压导线表面的面电荷等效为成对的线电荷。根据模拟线电荷、位置与匹配点位置的几何关系矩阵以及导线电压确定模拟线电荷的大小。子导线表面的电场强度便可以使用模拟线电荷与几何关系矩阵获得。此外,本文还研究了当输电线路导线高度、极间距、分裂间距和子导线半径等因素变化一定范围时,子导线表面标称电场强度的变化。
1 计算模型和方法
1.1 计算模型
对于高压导线和地面之间场域的电位分布,使用Laplace方程描述,即:

(1)
式中:φ为节点电位,V。
计算模型的边界条件为
a.导线表面电位U=±1100 kV;
b.地面电位U=0 V。
特高压直流±1100 kV输电杆塔的典型结构如图1所示[28]。设导线高度为H=27 m,极间距为Dp=28 m,导线分裂间距为Ds=0.5 m,子导线直径为Dc=4.8 cm。

图1 杆塔结构示意图
1.2 计算方法
本文使用模拟电荷法计算±1100 kV特高压直流输电子导线表面的标称电场分布。模拟电荷法(CSM)是计算电场分布的主要方法之一。该方法将金属电极表面连续分布的自由电荷用一组离散化的模拟电荷进行替代。只要通过一定条件算出模拟电荷,即可实现等效替代。模拟电荷法可看作是广义的镜像法,但该方法在数值处理和工程应用上,优于镜像法[23]。
对于高压导线表面电场强度的计算,首先在导线内部区域同心地设置n个模拟线电荷Qi,根据镜像原理,所设置的线电荷是成对的。然后在导线表面,设定数量等同于模拟电荷数目的匹配点Mj。匹配点的电位为导线电位。
根据电位叠加原理,对应于各匹配点Mj,可以逐一列写由设定的模拟电荷所建立的电位方程组[23]:
(2)
写成矩阵形式,得到:
[P]{Q}={φ}
(3)
式中:[P]为根据模拟电荷和匹配点之间的几何关系所形成的系数矩阵,方阵中的元素Pij为[32-33]
(4)
式中:ε为空气的介电常数,8.85×10-12F/m;(xi,yi)为第i个匹配点坐标;(Xj, -Yj)与(Xj,Yj)为第j对模拟线电荷的坐标。
求解矩阵方程式(3),得到各个模拟电荷{Q}。然后在高压导线表面选取若干个校验点,计算模拟电荷法的精度。计算表明,模拟电荷法计算电位和场强的精度能达到万分之一,甚至十万分之一。最后,利用{Q}计算导线表面各点的电场强度,完成计算。
2 计算结果和影响因素分析
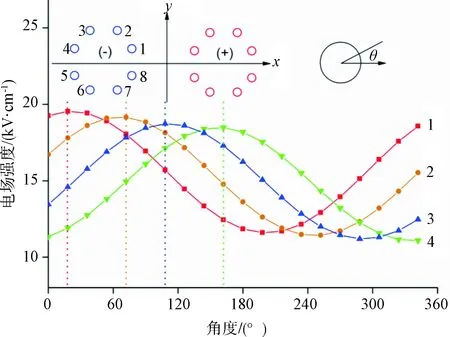
±1100 kV特高压直流输电杆塔的结构示意图如图1所示。设导线高度为H,极间距为Dp,子导线分裂间距为Ds,导线半径为Dr。在正负极的8个导线表面,标称电场强度分布的计算结果如图2所示。线路结构为H=27 m,Dp=28 m,Ds=0.5 m,Dc=4.8 cm。根据电场分布的对称性,每根正极性子导线表面的场强大小等于与之对称分布的负极性子导线表面的场强大小。
图2中的横纵坐标分别是极角θ和与极角对应的场强大小E。E-θ曲线与正弦函数图像相近。子导线上场强最大值出现在1号子导线上,为19.54 kV/cm,因为该处位置与对侧极导线相距较近。此外,由图2还可见,各条子导线表面场强最大值对应的角度随导线序号而增加。

(b)图2 子导线表面标称电场强度的计算结果
每条子导线表面电场强度的最大值随导线高度H的变化关系如图3所示。极间距、子导线分裂间距、子导线半径的取值与图1相同。由图3可见,子导线表面电场强度随导线高度的增加而减小。当H从25 m增加到29 m时,即增加了16%,第6号子导线表面最大场强的变化最明显,但也仅减小了1.1%,从19.00 kV/cm减至18.79 kV/cm;第1号子导线表面最大场强的变化最不明显,仅仅减小了0.6%,从19.61 kV/cm减至19.49 kV/cm。
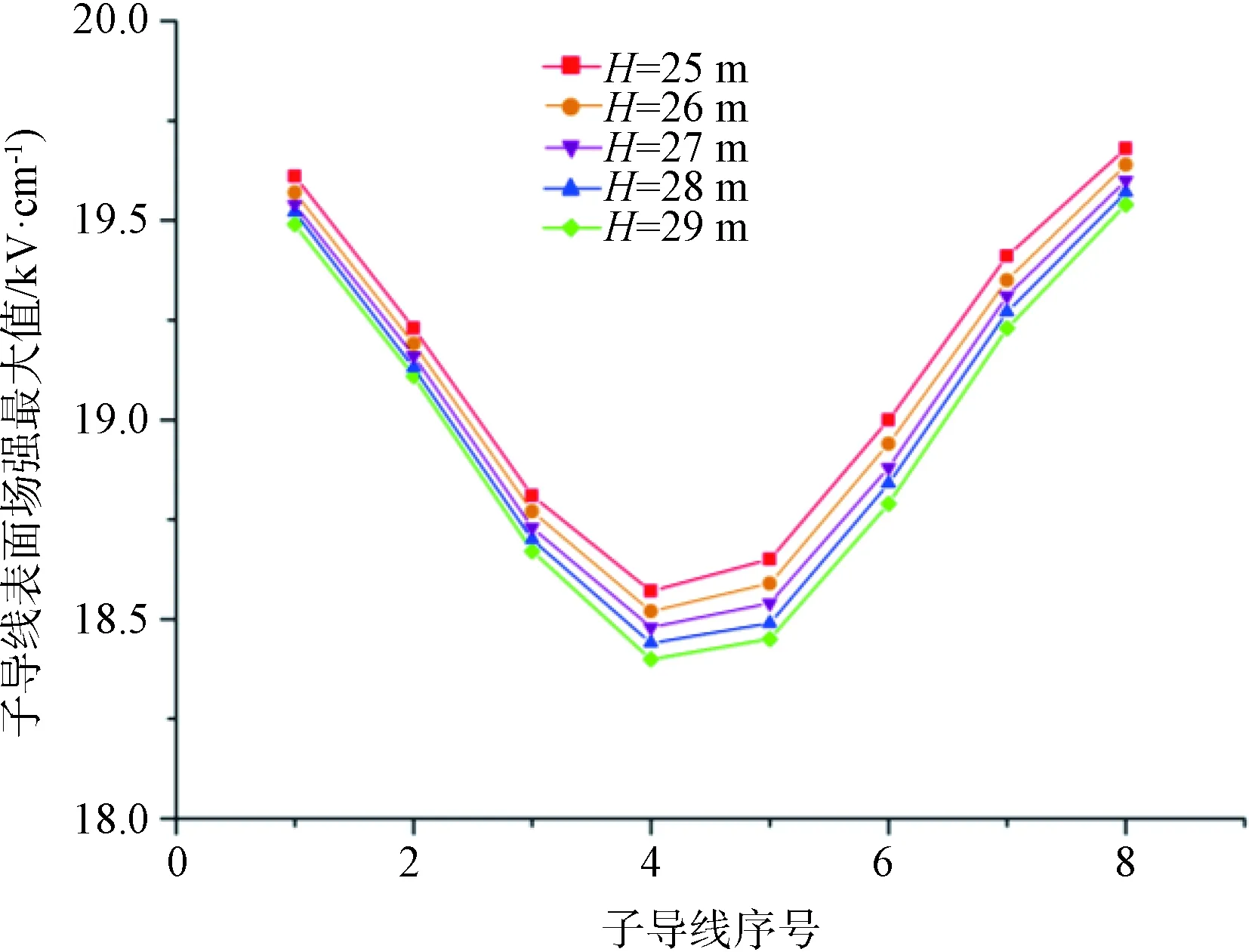
图3 子导线表面场强最大值随导线高度的变化
每条子导线表面电场强度的最大值随极间距Dp的变化关系如图4所示。导线高度、子导线分裂间距、子导线半径的取值与图1相同。计算表明,各条子导线表面电场强度的最大值随极间距的增加而减小。当极间距从26 m增至30 m时(增加了15.4%),第6号子导线表面最大场强的变化最明显,减小了3.5%,从19.92 kV/cm减至19.22 kV/cm;各条子导线表面最大场强平均降低3%。

图4 子导线表面场强最大值随极间距的变化
每条子导线表面电场强度的最大值随分裂间距Ds的变化关系如图5所示。导线高度、极间距、子导线半径的取值与图1相同。由图5可见,各条子导线表面电场强度的最大值随分裂间距的变化不明显。当分裂间距从0.46 m增至0.54 m时(增加了17.4%),各条子导线表面最大场强的变化量均小于1%。

图5 子导线表面场强最大值随分裂间距的变化
每条子导线表面电场强度的最大值随子导线直径Dc的变化关系如图6所示。导线高度、极间距、分裂间距的取值与图1相同。计算表明,各条子导线表面最大电场强度随子导线半径的增加而明显减小。当子导线直径从4.4 cm增至5.2 cm时(增加了18.2%),第5号子导线表面最大场强降幅最大,为12.0%。其余各条子导线表面最大场强的变化量也都接近12%。因此,与导线高度、极间距、分裂间距相比,子导线直径是影响子导线表面场强最显著的几何参数。
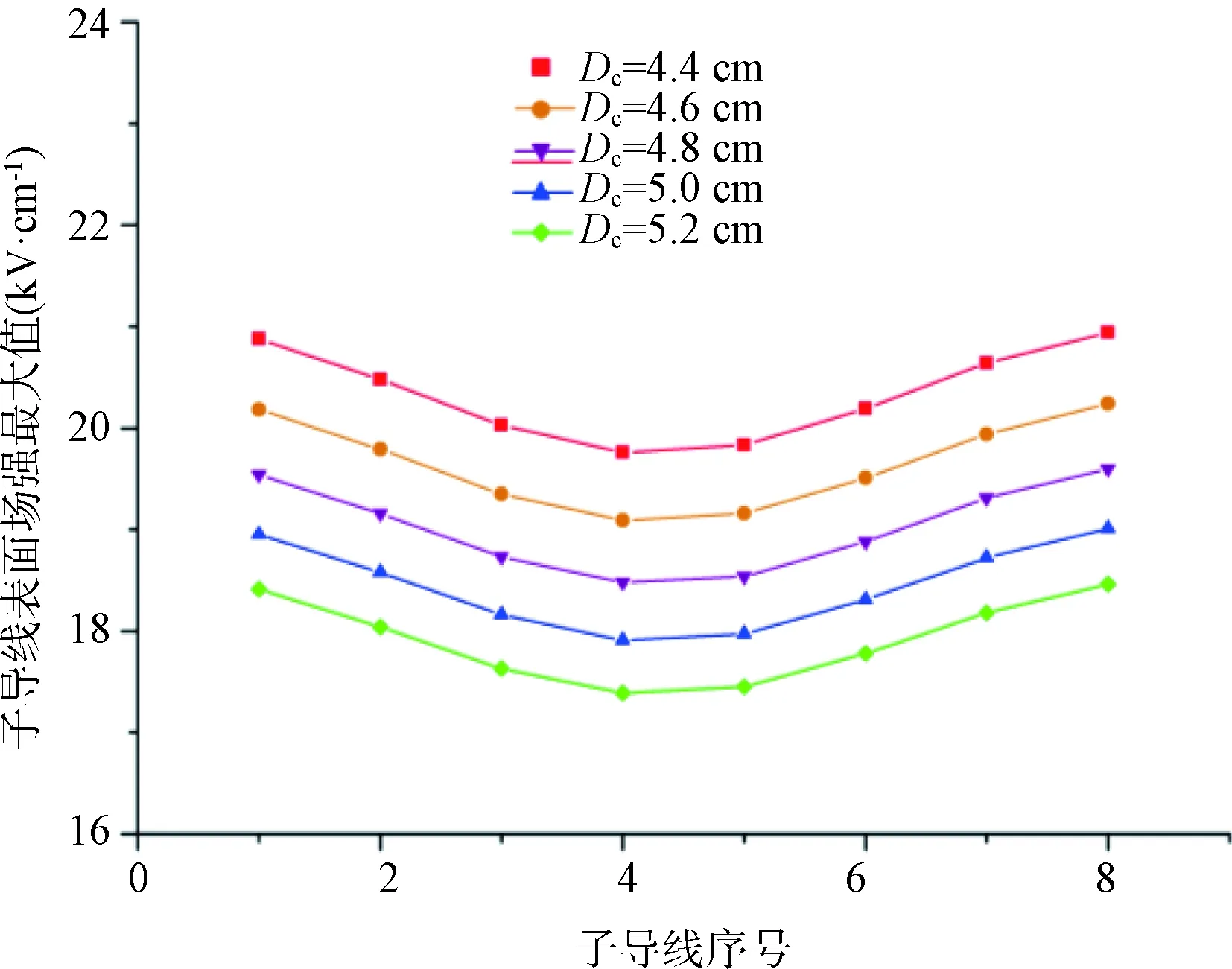
图6 子导线表面场强最大值随子导线直径的变化
3 线路电磁环境分析
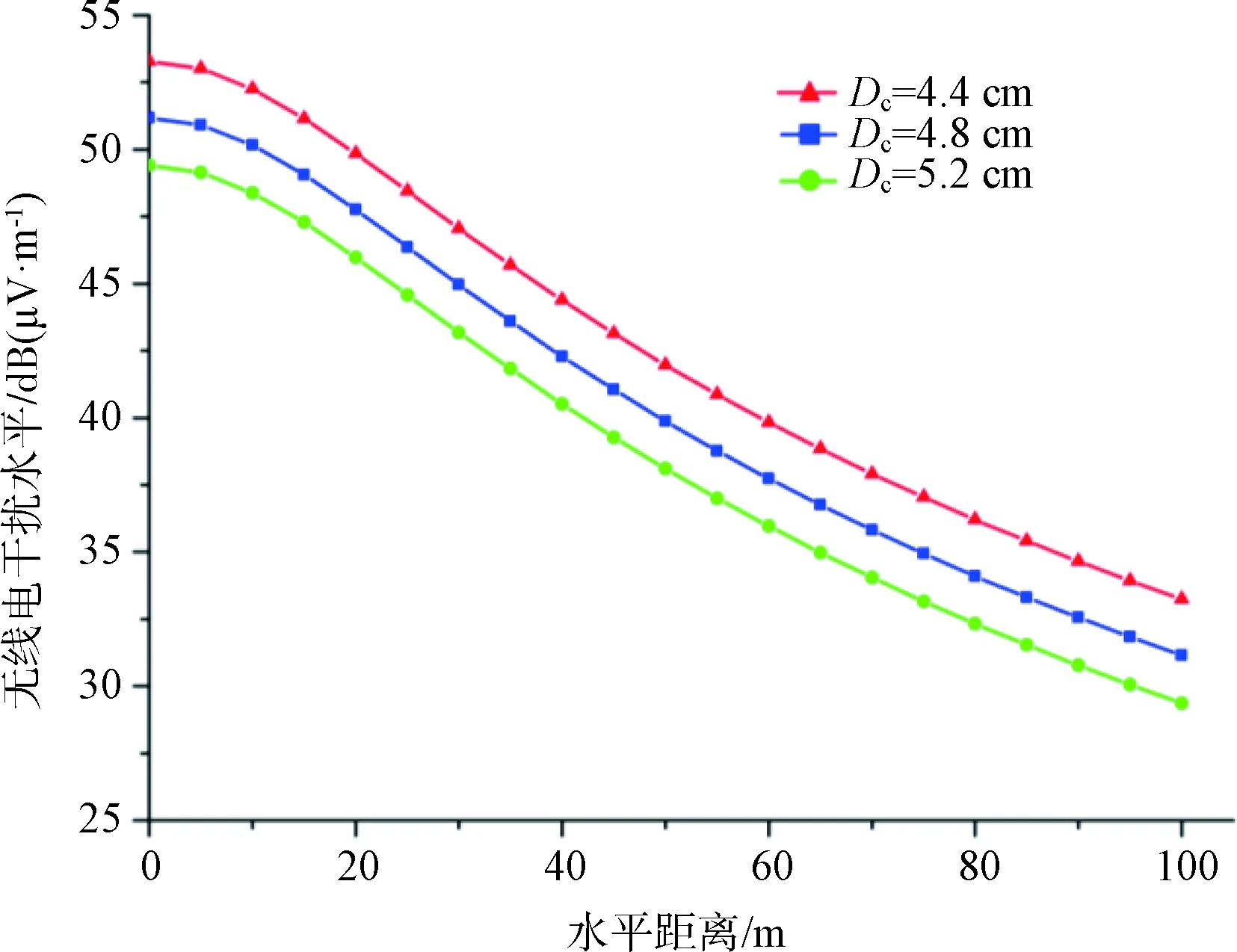
无线电干扰和可听噪声水平是描述输电线路重要的电磁环境参数。基于导线表面电场强度的结果,可以计算无线电干扰RI和可听噪声AN,结果如图7(a)和图7(b)所示。根据标准[34-35],线路无线电干扰和可听噪声的计算公式如式(5)、式(6),观测点的对地高度是1.5 m,导线结构尺寸与图1相同。
(a)
(a)

(5)
AN=-133.4+86logEmax+40log(0.66Dc·n0.64)-11.4logd
(6)
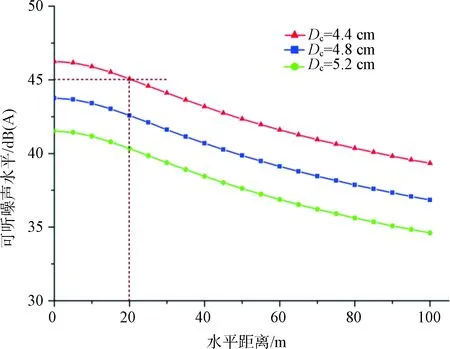
(b)图7 无线电干扰和可听噪声的计算结果
式中:Emax为导线表面最大场强值,kV/m;n为导线分裂数,n=8;d为观测高度,d=1.5 m。
计算结果表明,无线电干扰小于电磁环境限值55 dB。当子导线半径大于4.4 cm时,距导线水平距离20 m处的可听噪声也未超过限值45 dB (A)。
4 结论
本文基于模拟电荷法计算了±1100 kV特高压直流输电导线表面的标称电场强度,并对其影响因素进行了定量分析。获得了导线高度、极间距、分裂间距和子导线半径变化时,各条子导线表面电场强度的变化规律;通过计算表明,与导线高度、极间距、分裂间距相比,子导线直径是影响子导线表面场强最显著的几何参数。当其他因素不变时,子导线表面场强的变化与子导线直径的变化在同一数量级;子导线表面场强的变化比导线高度、极间距、分裂间距的变化小一个数量级。根据本文使用的导线结构尺寸,输电线路的无线电干扰和可听噪声水平均未超过规定的限值。

