粉尘浓度测量装置利用涡流发生效应的优化研究
刘丹丹,温海蔚,赵文帝
(黑龙江科技大学电气与控制工程学院,黑龙江 哈尔滨 150022)
0 引言
近年来,随着现代工业和科学技术的迅速发展,各项粉尘数据的测量显得越来越重要。各类发电厂响应国家“节能减排”战略,对排放的流量有进行测量的硬性要求。因此,及时对粉尘浓度及流量进行检测具有重要意义。
现阶段,常规粉尘检测操作对于环境影响较大,会出现测量偏差和频繁操作等问题[1]。在国内,很多学者通过摩擦起电的原理对粉尘进行了研究。赵恩彪等[2-3]研究了利用电荷感应法测量粉尘密度的原理,并采用试验系统的方法研究了不同粉尘粒径下产生电荷之间的线性关系。陈建阁等[4]研究了粉尘质量流量的测量方法,得出环状探头适用于测量匀速且均匀分布颗粒体的结论。许传龙等[5]对环状探头的空间灵敏度进行了气固两相流分析,并分析了各种探头结构参数对该方法测量结果的影响。但是,粉尘带电量十分有限,使得探头感应量也很微弱。
本文为减少粉尘密度测量误差、提高粉尘浓度的测量精度,对现有粉尘检测管道的设计进行改造[6]。最终通过试验进行气固两相流仿真试验以及数据验证检验。该研究对粉尘检测装置的测量灵敏度研究有一定的意义。
1 现有传感器的结构和工作原理
当前,常用来测量和研究的粉尘静电传感器[7]可以分为三种类型:环状传感器、针状传感器和棒状传感器。棒状传感器属于对粉尘直接接触式的测量传感器,适合在大口径管道中测量粉尘数据,其优点为易于安装[8]。针状传感器和环状传感器特点相似,都属于非接触式静电传感器,采用镶嵌式安装,对于大口径管道安装成本较高、灵敏度高。本文研究对象为三种传感器中的环状传感器。
装置结构如图1 所示。
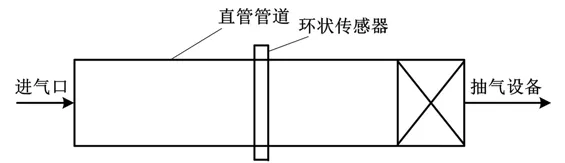
图1 装置结构图Fig.1 Structure of device
接触带电过程如图2 所示。
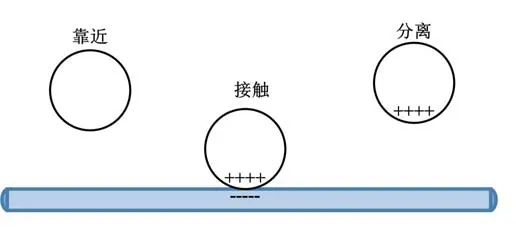
图2 接触带电过程示意图Fig.2 Contact charge process
同时,对于环形静电传感器而言,静电传感器能够根据测量所得信息得到流动平均速度。粉体的悬浮性使得粉体颗粒物与大地总是绝缘的,因此,每个颗粒都有可能带电[9]。普通颗粒物接触并产生电荷的过程为:固体的接触、分离和摩擦效果。本文着重对第一种起电方式进行研究。
需要研究的电荷Q与理论上接触装置的电荷Q0之间满足如下关系:

式中:f为逸散系数,取值范围是0 对现有静电传感器测量粉尘的不精确问题,提出利用文丘里效应与涡流发生器相结合的方法,对现有传感器的直管管道进行改进。 涡流发生器[10-11](vortex generator)于1947 年被美国联合飞机公司的 Banes 和Taver 提出。涡流发生器是垂直安装在机翼表面的、具有小展弦比特性的物体[12]。这使得处于逆压梯度中的边界层流场能量增加,从而使得气流能继续贴附在物体面上而不产生气流分离。这也恰好符合本管道流体吸附于管道面便于测量的标准。 涡流发生器广泛应用于流体研究各个领域的原因有很多,主要有几何形态简单流场中没有历史遗留旋涡,便于试验的研究观察;而且所在的流场中也会包含丰富的分离及涡运动形态,使得此发生器对基础研究有重要作用。对安装涡流发生器的模型作流体观察,可以看到其诱导超过边界层以外的高能气流贴近表面,从而可替代内层原本的低能气流。临近涡流发生器表面的气流会因为涡流发生器的作用提高内在能量,同时边界层的气流因能量变化使得整体流速得到提升,可抑制表面层便捷分离[13]。以上机理表明:加装涡流发生器的模型表面,流速增加、推迟或抑制了边界层分离。本文利用近几年这方面的研究成果,对文丘里管道[14-15]进行改进。 本研究在Pro Engineer 中建立3D 立体模型。根据相关文献,设置管道结构。管道中收缩段和扩散段管径为6 cm、长度为4 cm;喉道段管径为4 cm、长度为8 cm。涡流发生器在喉道段处,共设置3 个。根据气流稳定度以及对增速的要求,每个涡流发生器水平相距120°。出口和入口管口直径为16 cm。改进的管道结构如图3 所示。 图3 改进的管道结构示意图Fig.3 Improved pipeline structure 本设计的目的在于增加管道中央烟尘的气体流速并精确测量值。所以在管道中央设置的收缩口起到了压缩空气的作用,更易于汇聚压力。管道中的涡流发生器采用三角结构,三组器件在管道同截面设置间隔120°固定,对环状传感器的电荷量检测更加精确。三角翼形涡流发生器和文丘里管道的设计简洁、效果显著。当气体经过管道中央时,会在尾翼形成涡流,使得烟尘在气体旋涡的作用下更贴近于管壁运动。此优化对于气流的加速起到了更直接的作用。具体仿真操作如下:进 入ANSYS19.0 进行设置,选 择其中的Workbench 程序,构建3D 模型;提取流体并封闭左右管口,设置流体模式并禁用固体模式;进入网格模块,设置进口在左、出口在右,选择类型为默认类型。设置管壁:网格步长为2 mm、温度取自然温度300 K。 该设计使用Fluent19.0 对仿真条件进行设置。假设此管中的流动形态为稳态,采用Eulerian 模型计算相关数值并开启能量方程。颗粒设置:导热系数为0.3 W;密度为2 600 kg/m3;粘度为1.8e-05 Pa.s;比热容为1 200,单位的设置基于软件尺寸的选择;温度取自然温度295.10 K。相态中:主相为空气,副相为颗粒,粉尘颗粒受到曳力作用。空气的入口速度设为4 m/s。设置中,以粉尘不受到空间曳力的作用为佳,粉尘速度设为3 m/s,管壁内选择对流,自然对流系数取6,颗粒体积分数为0.012。在迭代计算时,动态显示计算残差,对应的精度均为0.001,管道进口的水力直径Volume Fraction 为0.15,设置迭代次数为6 000 次。 在设置上述模型的相关参数前提下,将粉尘颗粒直径设为1 μm、3 μm、5 μm、7 μm、10 μm、20 μm、30 μm、40 μm、50 μm,并进行仿真试验。在XOY面(Z-Coordinate)得到管道内流体的粉尘颗粒与空气混合的速度云图,并在ZOY面(X-Coordinate)得到管道侧面粉尘流通的速度云图。 通过仿真反馈的速度云图可以看出,管道内颗粒物在涡流发生器的作用下产生旋涡,并有效增大颗粒物流速。接下来,对比文丘里管道和三角涡流发生器的管道颗粒物运动情况,以7 μm 粒径大小作为测量结果进行观察。 7 μm 粒径速度云图如图4 所示。 图4 7 μm 粒径速度云图Fig.4 Velocity nephogram of the 7 μm particle diameter 通过读取改进管道试验仿真的速度云图,测得管道中间段的速度值,并且与项目组中研究的文丘里管道测得的速度值进行对比。基于此,可得到不同粒径下粉尘通过改进管道、文丘里管道、普通管道的颗粒速度对比结果。 不同粒径下的粉尘颗粒速度如表1 所示。 表1 不同粒径下的粉尘颗粒速度Tab.1 Dust particle velocity under dfifferent particle sizes 如表1 所示,在不同粒径下,改进管道相比另外2种管道而言,测得的速度值更高、效果更显著、在颗粒较小的情况下测得的速度值相对明显。 由表1 可知,改进管道的速度值明显高于直管。由于管道中涡流发生器的原因,混合气体通过管道时,会在尾翼处产生空气旋涡,更易使颗粒物充分接触环状电荷感应传感器。利用MATLAB 计算,由电荷量归一化可看出,改进管道整体感应电荷量提高20%,颗粒物在10 μm 以下时感应电荷量提高约30%。对速度和感应电荷量的综合分析,有助于测量的精准。 电荷量归一化结果如图5 所示。 图5 电荷量归一化结果Fig.5 Charge normalization results 对管道的电荷量采集进行理论认证。在改进管道前后进行模型的电荷量观察。将点电荷与极板中轴线的距离定义为x,取x为1,2,...,7,并对电荷量进行分析。 装置改进前后,x对荷电的影响如表2 所示。 表2 x 对荷电的影响Tab.2 x effect on the charge 综合表2 数据,绘制函数折线图。改进前后感应电荷对比如图6 所示。 图6 改进前后感应电荷对比Fig.6 Comparison of induction charge before and after improvement 由图6 可知,改进管道的电荷量更大,即粉尘浓度检查对于此管道的检测效果更佳。 静电传感器数学模型如图7 所示。 图7 静电传感器数学模型Fig.7 Static sensor mathematical model 目前来说,英国Kent 大学Yan Yong 教授[16-17]在应用静电感应原理研究颗粒流动参数方面处于领先地位,并做出了一定成绩。在点电荷研究的基础上,通过感应电荷的数学模型计算环状传感器所得电量。 式(2)、式(3)为环状传感器电荷量计算公式。 式中:z为颗粒速度v与时间的乘积;w为极板宽度;q为以一定速度通过极板的点电荷;D为环形极板的直径;Q为极板上的感应电荷量;x为感应电荷与极板中轴线的距离。 利用MATLAB2019a 软件生成数学模型,导入各粒径颗粒物通过管道的速度值,计算得到感应电荷量。根据数据计算,得到文丘里管道和改进管道的感应电荷量值;通过数据进行比较,证明研究可行性。 根据环形静电传感器的感应电荷量计算公式和表1 数据,利用MATLAB2019a 进行计算,得到改进管道的感应电荷量,并与项目组研究的文丘里管道的感应电荷量进行对比[18]。其粒径不同时所带感应电荷量的增加率如图8 所示。 图8 感应电荷量的增加率Fig.8 Induction charge increase rate 通过对比图6、图8 可知,改进管道相对于文丘里管道而言,感应电荷量有了明显的提升。尤其在1~20 μm 的粒径下,改进管道测量效果更加明显。 利用现有的静电感应式粉尘浓度传感器的工作原理,研究分析仪器在低浓度环境下的测量精确性问题,并结合影响静电感应信号的因素,使用文丘里管道和涡流发生器相结合的方法对粉尘浓度进行测量。在10 μm 以下的小粒径当中,颗粒物速度提升约24%。以7 μm 粒径为例,粉尘在管道内运动速度从7.55 m/s 提升至10.41 m/s,使测量精度和测量水平稳定提高。 利用PROE 5.0 软件构建3D 模型,导入Fluent软件进行数据仿真。根据仿真结果和数据对比分析,改进的测量管道与项目组研究的文丘里管道相比,其测量精度得到提高。利用MATLAB,通过电感应计算式计算感应电荷量,可得:感应电荷量与文丘里管道相比,能使小粒径粉尘的电荷量平均提高23.75%,整体感应电荷量提高,更有利于传感器接收到颗粒物静电信号。 最后,在测量粉尘数据的同时也会产生不同种类的误差。由于电荷感应测量方法也有影响因素需要及时标定,后续会研究对其进行因素补偿。2 静电传感器的优化设计
2.1 设计原理和优势分析
2.2 几何模型的建立

3 仿真结果及对比分析
3.1 仿真图的分析

3.2 数据对比分析




4 环形静电传感器
4.1 数学模型和感应电荷计算式

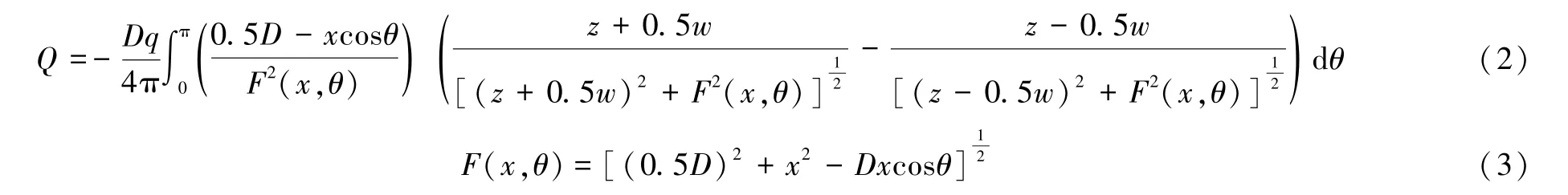
4.2 感应电荷量对比分析

5 结论

