求解机器人双边装配线平衡的莱维-灰狼优化算法研究

王惠敏,苏莹莹

(沈阳大学机械工程学院,辽宁 沈阳 110044)

0 引言

装配线广泛应用于制造业。如何利用有效的方法平衡和优化装配线,一直是制造业和学术界关注的焦点。求解装配线平衡问题的目的是减少不平衡工时、降低工时损失、有效提高设备利用率、减少在制品,从而提高装配线的生产效率、提升企业效益。装配线按照自动化程度可以分为人工装配线、人-机装配线以及机器人装配线。

随着机器人越来越广泛地应用在装配线上,产品的装配效率也越来越高,在一定程度上提高了企业的效益。然而,机器人在运转工作的时候,也会带来一定的能源消耗,以及投入的机器人成本。因此,在对机器人装配线平衡问题进行优化时,如何在节拍最小化、降低机器人能耗以及机器人成本之间寻找一个契合点,已成为科研工作者工作的重心。

吴意等[1]针对双边装配线平衡问题考虑了多种约束条件,并构造了一种改进的万有引力搜索算法,以解决问题。詹慧文等[2]建立了双边装配线平衡的多目标优化模型,提出了拓扑排序矩阵编码方法、面向位置约束的解码方法、变邻域搜索策略,与标准蝙蝠算法相结合,对标杆算例进行求解。Zhong[3]以优化循环时间为目标,建立了混合整数线性规划模型,并考虑顺序相关和机器人的装配时间。周炳海等[4]提出了最小化工作站数量和工作站占用空间的目标模型,并以改进的多目标免疫克隆算法求解。Zhong 等[5]建立了以最小化装配成本和最小化工作站数量为目标的数学模型,并提出了一种离散人工鱼群算法来求解。CIL 等[6]研究了混合模型RALBP-Ⅱ,提出了一种优化所有模型总节拍的波束搜索算法。Zhang 等[7]针对装配线平衡和能源消耗,建立了考虑能耗和平衡率的双目标优化数学模型;在对模型求解时,采用了一种结合细胞策略和局部搜索的多目标智能优化算法。蒙凯等[8]建立了以能耗最小为优化目标的数学模型,考虑了工序间的优先关系约束、节拍约束,并用灰狼算法来求解。Fysikopoulos 等[9]指出,在汽车制造过程中,能源成本占总成本的9%～12%,其中主要能源成本是机器人在装配任务中所消耗的能源成本,而发电所产生的二氧化碳排放量占工厂总排放量的20%。Li 等[10]针对机器人双边装配线建立了总能耗和节拍最小的双目标模型,并用模拟退火算法求解。Nilakantan 等[11]提出了装配线最小总碳足迹和最大装配线效率的数学优化模型。

现阶段的研究主要是对机器人装配线进行单一目标或双目标优化,而未对其节拍、能耗和成本组成的多目标集合进行优化。在机器人装配线上,不仅节拍是主要的影响因素,能耗和机器人投入成本更是直接决定了投资成本。

1 问题描述

双边装配线的特点是:装配线长度较短,可以有效地缩短线上产品的生产时间;设备利用率高,可以减少投入的设备成本,从而应用于汽车、卡车、摩托车等制造业。双边装配线除一些基本约束外,还包括位置约束、区域约束、同步约束等。

双边装配线的工位布局如图1 所示。

图1 双边装配线的工位布局图Fig.1 Station layout of two-sided assembly line

建立机器人双边装配线平衡的数学模型,需要对以下条件作假设:产品的装配工序时间已经确定,工序逻辑优先级关系已知;所有操作都只分配到其中一个工作站;工作站的数量已经确定;每个工作站之间由传送带连接,传送速度是一定的,可以忽略传送时间,每相隔固定的节拍时间放置一个待装配的零件。加工能耗是单位时间加工能耗与加工时间的乘积。待机能耗是单位时间待机能耗与待机时间的乘积。建立模型如下:

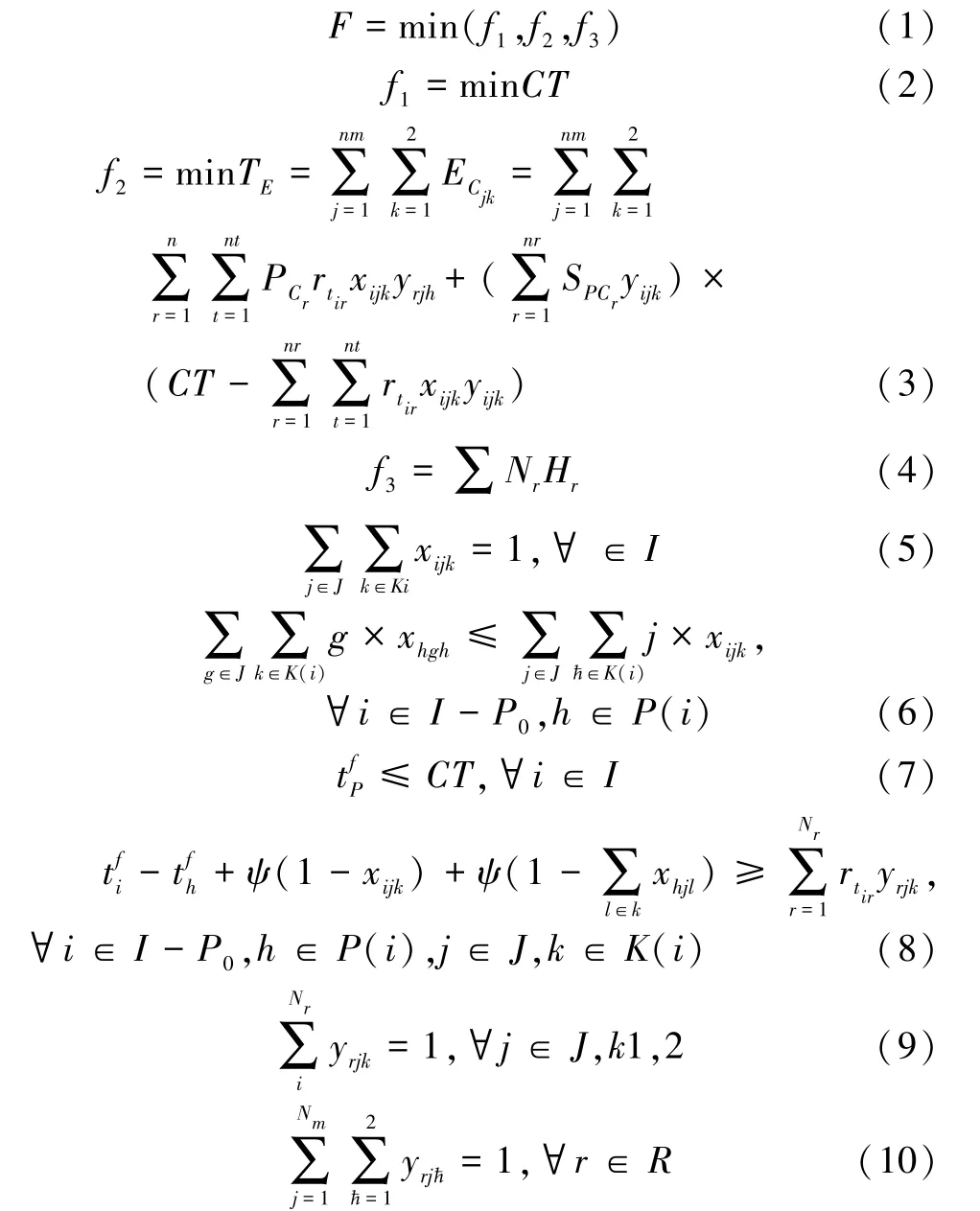
式中:r为机器类型;Nr为机器数量;R为机器类型集合,R={1,2,…,r,…,nr};rtir为操作i在机器r上的加工时间;Yrjk为PCr为机器r单位时间内的加工能耗;SPCr为机器r单位时间内的待机能耗;ECjk为工位(j,k)的能耗;TE为装配线的总能耗;Hr为机器人r的成本。

式(1)为优化目标。式(2)为最小化生产节拍。式(3)为最小化总能耗。式(4)为最小化机器人成本。式(5)为操作分配约束,要求每个工序必须成对分配到工作站的一侧。式(6)为优先关系约束,要求操作工序的前一工序必须被分配到靠前或者相同的成对工作站。式(7)为生产节拍约束,要求每个工序的完成时间须得小于或等于节拍时间。式(8)为成对工位操作内的优先关系约束。式(9)要求每个工作站必须分配有一个机器人。式(10)要求每个机器人必须被分配到一个工作站。

2 莱维飞行和灰狼优化算法

2.1 莱维飞行简介

莱维(Levy)飞行[12]是一种理想的捕食方式,其特点是长时间短距离运动和偶尔长距离运动,以确保游动不会停留在某一局部区域。因此,一部分解在当前最优值的附近进行搜索,加快了局部搜索速度;另一个部分解在距离当前最优值足够远的空间中搜索,避免系统陷入局部搜索。在布谷鸟搜索算法中,Yang[13]利用Levy分布特征函数,经过变换得到如下概率密度函数:

在布谷鸟搜索算法中,通常使用式(12)计算莱维随机数:

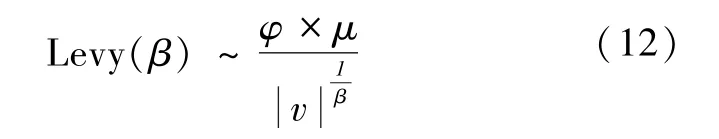
式中:μ、v服从标准正态分布;β=1.5。

φ的数学定义为:

2.2 灰狼优化算法

灰狼优化(grey wolf optimizer,GWO)算法是受灰狼群体捕食行为启发,所研究出的一种群智能优化算法。该算法收敛性强、参数少、易于实现[14]。

2.2.1 灰狼算法基本原理

灰狼是群居生活的动物,在食物链中处于顶端。灰狼群体严格遵守等级关系。狼群的组织结构根据领导权力进行分级,主要分为4 个等级:α、β、δ、ω。低等级的狼服从于高等级的。

在狩猎过程中,主要寻优过程是由ω狼分散包围猎物,其他3 个等级的狼根据收集到的信息指挥ω狼的移动方向,并决定是否更新自己的位置;当满足终止条件以后,输出最优解[15-16]。图2 为灰狼种群层级金字塔图。

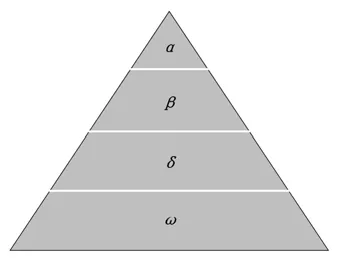
图2 灰狼种群层级金字塔图Fig.2 Hierarchical pyramid of gray wolf population

2.2.2 灰狼行为

在灰狼算法中,灰狼的行为主要包括以下3 种。

①搜索。

狼群搜索猎物的过程主要由灰狼α、β、δ的指引来实现。在模拟此行为时,假定α、β、δ能识别隐藏猎物的位置。因此,每次进行迭代计算,保留当前种群中最好的3 个灰狼(α、β、δ),而后依据它们的位置更新其他灰狼的位置[17-18]。该行为的数学模型表示如下:

式中:Xα、Xβ、Xδ分别为当前种群中α、β、δ的位置;X为灰狼的位置;Dα、Dβ、Dδ分别为目前ω狼与α、β、δ狼之间的距离。

当|A|>1 时,灰狼尽可能地分散在不同的区域,寻找猎物;当|A|<1 时,灰狼将会聚集在同一个或多个区域寻找猎物。

②包围猎物。

在包围的过程中,猎物与灰狼个体的位置可以表示为:

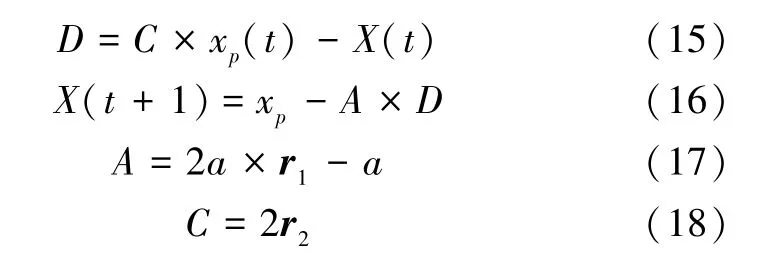
式中:t为迭代次数;xp为猎物的位置;X为灰狼的位置;A、C为向量的系数;r1和r2为数值在 [0 1 ]之中的随机向量[19]。

在整个迭代计算过程中,a从2 线性降到0。

③袭击猎物。

在建立此行为模型的过程中,当猎物停止移动时,灰狼群开始袭击猎物,灰狼群的狩猎行为结束。在算法进行到后期时,可以通过将收敛因子a从2 线性地减少到0 来模拟此过程。当|A|≤1 时,灰狼群体开始袭击猎物。灰狼群体的袭击行为仿真使灰狼算法具有良好的局部精细搜索能力[19-20]。

2.3 基于莱维飞行的灰狼优化算法

2.3.1 基本原理

优化算法在原灰狼优化算法中,最优解即为α狼的位置。由于存在精英保存策略,在GWO 算法后期,群体中所有的灰狼个体都接近最优个体α狼,从而丧失了种群的多样性,使算法陷入局部收敛。针对这些不足之处,本文研究基于莱维飞行的灰狼优化(Levy-GWO)算法,采用莱维飞行来全局搜索群体中的灰狼个体α狼。莱维飞行属于随机行走,是一种很好的搜索策略。它可以扩大搜索范围,飞行步长满足稳定分布。在莱维飞行中,新一代α狼的计算公式如下:

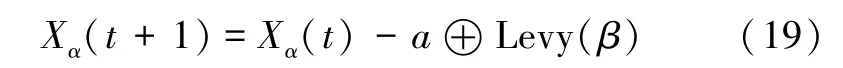
式中:X(t)为第t代时灰狼个体α狼的位置;⊕为点对点乘法;a为α狼位置的随机数,由式(20)决定;Levy(β)为随机搜索路径,由式(21)决定。

2.3.2 算法流程

Levy-GWO 算法的算法流程如图3 所示。

图3 Levy-GWO 算法流程图Fig.3 Levy-GWO algorithm flowchart

算法流程如下。

①输入。输入装配线平衡问题数据。

②数值初始化。初始化灰狼种群、灰狼个体的位置和目标函数值。

③选出头狼α狼。遍历灰狼群的所有个体,计算出狼群个体的适应度值。选取最优值为α狼(即头狼),β狼为次优,其余为δ狼和ω狼。

④更新狼群位置。根据式(1)更新α狼位置,同时利用莱维飞行和灰狼算法结合得出的式(20)～式(22)全局搜索α狼;计算出每次迭代所得的a、A、C等参数值。

⑤计算每只狼在新位置的适应度值。若新个体的适应度值优于旧个体,则更新新一代个体,由新个体替换原来的位置,并更新适应度值。反之,保留旧个体,原来的适应度值保持不变。

⑥包围猎物。按照式(5)～式(11)更新参与围攻行为的α狼、β狼、δ狼位置,对猎物实施围攻行为。当|A|≤1 时,进行下一步袭击猎物行为。

⑦如果达到迭代终止条件,则输出头狼的位置;反之,转步骤③。

3 基于Levy-GWO 算法的机器人双边装配线平衡

GWO 算法具有局部搜索能力强、收敛速度快、易于编程实现等特点,但存在全局搜索能力较弱、易陷入局部收敛早熟等不足。在算法中,引入莱维飞行对群体中α 狼展开全局搜索,扩大搜索范围。

3.1 编码

机器人双边装配线涉及工序和机器人的作业分配。因此,需要在种群初始化时,完成工序编码和机器人编码工作。

双边装配线平衡问题属于离散问题。GWO 算法多用于求解连续性问题。因此,工序编码采用随机数编码方式,以实现连续问题转换为离散问题。此编码包含N个要素,每个元素都是[0～1]之间的随机数,每个位置的随机数表示相应操作的权重。N代表搜索空间维度,即任务数。假设任务的随机数越低,则优先级越高,并按照由高至低的顺序排序任务的优先级。例如,任务8的随机数0.25 具有最高的最小优先级,因此它在操作序列中排名第一。以此类推,可以获得操作序列(8、2、10、3、6、9、7、1、4、5)。任务随机数如表1 所示 。

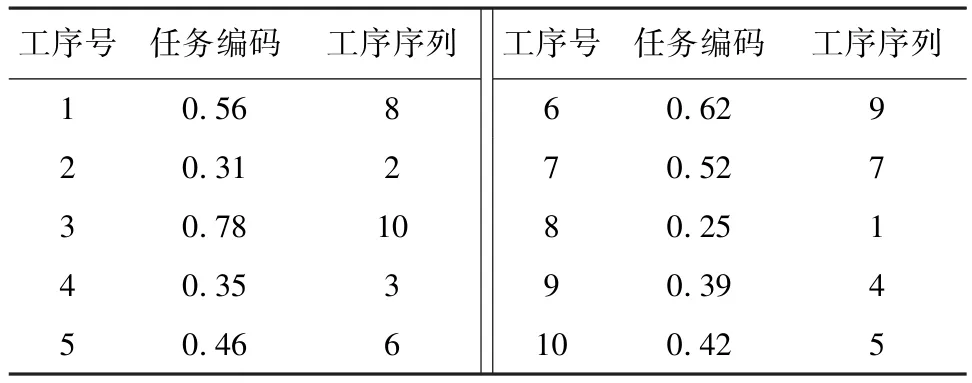
表1 任务随机数Tab.1 Task random number

3.2 解码

解码中,考虑工序优先关系、节拍约束、位置关系以及工序内的优先关系。

解码方式可进一步得到工作站的供需分布和适应度函数值。具体步骤如下。

①初始节拍值为:

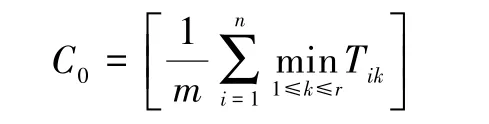
令当前的节拍C=C0,工作站序号j=1。

②根据操作序列分配顺序,将操作i分配给工作站j。如果分配的工作站的装配时间大于节拍C,则工作站编号j←j+1 。

③重复步骤②,直至所有操作分配完成。

④如果工作站的数量大于m,则令C←C+1,转步骤②。

⑤计算节拍、能耗以及机器人成本。

莱维飞行:根据灰狼算法的原理,利用3 只适应度最好的灰狼(α、β、δ) 来引导其余灰狼ω包围猎物并更新位置。

4 实例应用及分析

X 汽车公司作为汽车生产行业的佼佼者,其车身车间装配线大多采用机器人装配线。为验证算法的可行性,从X 公司汽车车身装配线上截取5 个成对工位,共40 个任务;每个工位上有1 个机器人,共10 个机器人;每个成对工位的初始节拍为149 s。机器人的能耗主要为电力消耗,机器人每工作1 h,其能耗(包括工作能耗和待机能耗)为406 kW·h,机器人总成本为210 万元。用MATLAB 2018 软件编写程序,进行求解寻优,所得结果如表2～表4 所示,优化曲线如图4～图6 所示。

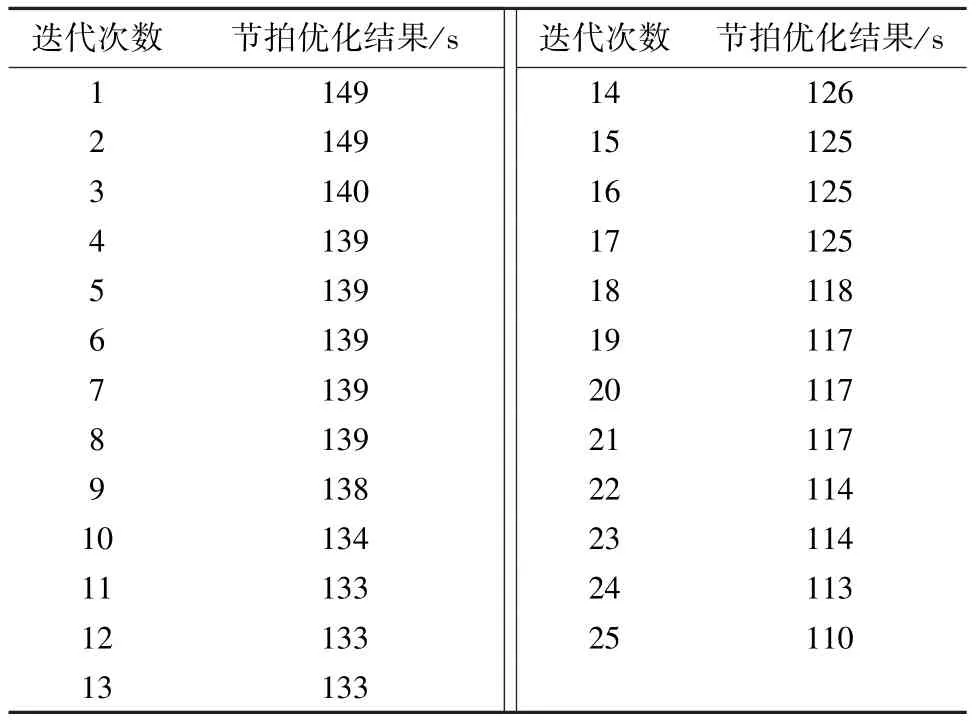
表2 节拍优化结果Tab.2 Beat optimization results

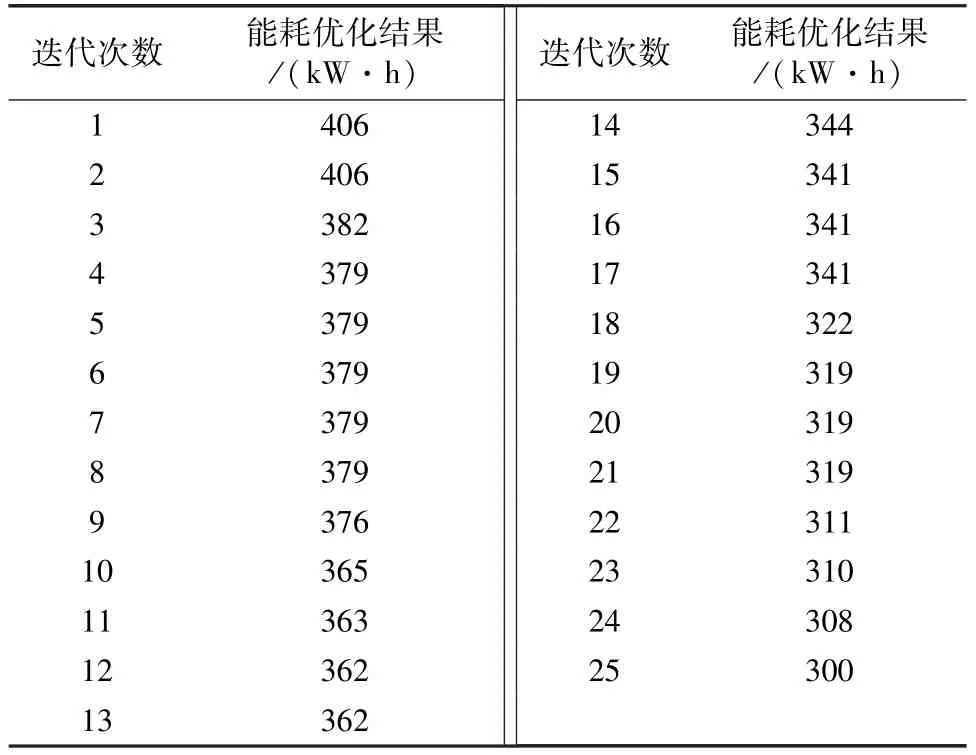
表3 能耗优化结果Tab.3 Energy consumption optimization results

表4 成本优化结果Tab.4 Cost optimization results

图4 节拍优化曲线Fig.4 Beat optimization curve

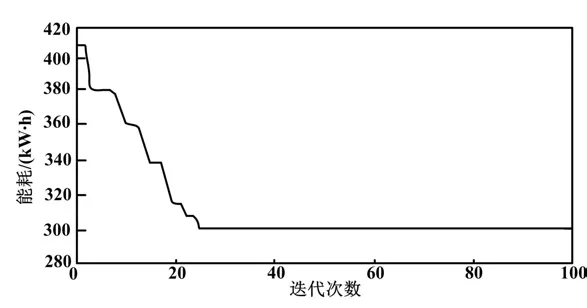
图5 能耗优化曲线Fig.5 Energy consumption optimization curve

图6 成本优化曲线Fig.6 Cost optimization curve

由求解所得各目标函数的解和优化结果可知,通过灰狼算法结合莱维飞行进行求解之后,节拍优化了39 s,能耗优化了106 kW·h,机器人投入成本优化了39 万元。经过优化,在缩短节拍、提高生产效率的同时,也减少了能耗投入和建线时的机器人成本投入,一定程度地降低了企业的生产成本。

5 结论

综合上述分析可知,案例的结果进一步验证了Levy-GWO 算法的可行性与有效性。操作分配约束、作业优先约束、位置约束增加了机器人双边装配线问题的复杂性,将莱维飞行与灰狼算法结合,可以有效提高算法的全局搜索能力。在更新狼群位置的过程中,莱维飞行可以保证搜索范围的全局性,提高了灰狼算法的全局搜索寻优能力。该研究为企业提高生产效率、减少成本投入提供了新思路和新方法。