基于VMD 的广义二次互相关时延估计方法

李 宏田 雷路敬祎刘庆强

(东北石油大学a.电气信息工程学院;b.人工智能能源研究院;c.黑龙江省网络化重点实验室,黑龙江 大庆 163318)

0 引 言

时间延迟作为信号特征的一个重要参数,随着信号处理技术的飞速发展,时延估计算法逐渐成为众多学者的研究热点[1]。无论是油气管道泄漏点的定位、卫星干扰源定位,还是麦克风阵列对语音信号的定位,时延估计都是一个必不可少的核心问题[2]。

目前,在众多时延估计算法中使用最广泛的算法是广义互相关时延估计,但该方法在噪声环境中性能会大幅降低[3],许多学者也正在针对此问题进行改进。唐娟等[4]提出的二次相关法具有一定的噪声抑制作用,略微提高了估计性能。周康辉等[5]提出的广义二次相关法对于低信噪比的条件下做了部分改进。殷恒刚[6]将小波变换与二次相关相结合,增强了时延估计的抗噪性能。钱隆彦等[7]改进的广义二次相关法和茅惠达等[8]结合相关峰精确插值改进的广义互相关法可以改善估计性能,提高估计精度。魏文亮等[9]将奇异值分解与互相关时延估计相结合,改善了低信噪比下的时延估计性能。变分模态分解能有效地将含噪信号中的噪声分量与有效分量分离,依据豪斯多夫距离能筛选出有效分量并重构信号,完成信号去噪。

结合变分模态分解与广义二次互相关时延估计算法的特点,笔者提出一种基于VMD(Variational Mode Decomposition)的广义二次互相关时延估计算法,实验表明其可以有效提高时延估计性能和精度,具有良好的抗噪性能[10]。

1 VMD降噪

1.1 基本原理

变分模态分解(VMD)可以有效地分离有效模态和噪声模态。假设输入信号为x(t),VMD将x(t)分解成K个本征模态函数(fBLIMFs),这K个模态可以复现原始输入信号。公式如下

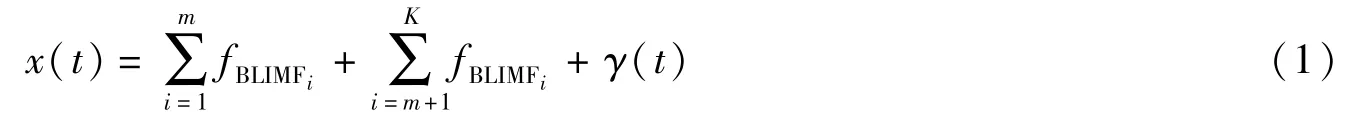
其中m为低频分量的个数,K为经VMD分解后的fBLIMF数量,γ(t)为残余分量。因为VMD分解的分量是从低频向高频分布的,所以fBLIMF1到fBLIMFm为低频有效分量,而fBLIMFm+1到fBLIMFk为高频噪声分量[11]。由此可得与输入信号相似的信号为

如何准确地判断从低频到高频的转折点成为能否得到最优重构信号的关键。

1.2 豪斯多夫距离

豪斯多夫距离(HD:Hausdorff Distance,DHD)作为一个非线性算子,不仅适用于评价几何图形之间的相似性,也可以将其用于建立概率密度函数(PDF:Probability Density Function)几何分布之间的相似性评价指标[12]。用P和Q表示两个点集,定义如下

HD对异常值非常敏感,通过计算K个分量与原信号的概率密度函数之间的Hausdorff距离,以此距离表示分量与原信号的相似程度,定义其为

1.3 VMD-HD降噪方法

x(t)经过变分模态分解成K个fBLIMF,然后根据豪斯多夫距离判断有效模态和噪声模态的分界点。HD是通过计算出两个fBLIMF之间的增量判别与原信号的相关性是否降低。当增量明显变大时,说明这个fBLMF与原信号的相关程度降低,定义最大增量为

由此,结合VMD和HD可以进行信号的分解和重构,以达到去噪目的[13]。

2 广义二次互相关方法

广义互相关时延估计方法(GCC:Generalized Cross-Correlation)是实际应用中使用最广泛的一种方法[14]。在GCC方法中,可利用加权函数提高信号的有效成分,通过计算两路信号的互相关函数获取峰值,从而得到时延值。假设接收信号模型为

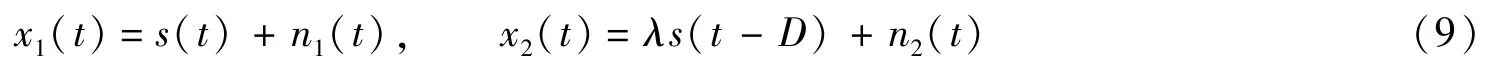
其中s(t)为源信号,而x1(t)和x2(t)为传感器接收的两路加噪信号;n1(t)和n2(t)为加入两路信号的噪声;信号的时延值为为信号幅度比值。广义互相关时延估计的基本原理如下

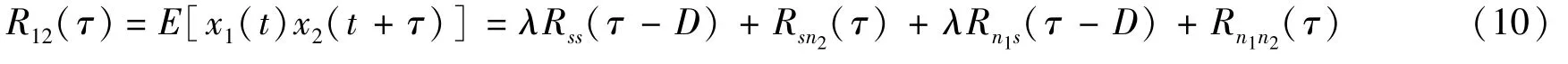
其中Rss(τ-D)为信源信号做二次互相关,Rn1n2(τ)为噪声做二次互相关[15],R12(τ)为x1(t)和x2(t)的互相关函数;理想情况下,噪声是独立于信源信号的平稳不相关的高斯白噪声,则Rn1s(τ-D)=0,Rn1n2(τ)=0,Rsn2(τ)=0,因此可以得到R12(τ)=λRss(τ-D)。由自相关函数的性质可得,当τ=D时,R12(τ)取最大值,即对应为两路信号的时延值。

广义二次互相关方法(GSCC:Generalized Second Cross-Correlation)是首先对x1(t)进行自相关运算,得到自相关函数,同时对x1(t)和x2(t)进行互相关运算,得到互相关函数,然后将得到的自相关函数和互相关函数再进行互相关运算,得到二次相关函数值。同时将二次相关函数值与广义加权函数相乘,得到广义二次相关函数,最后进行时延估计,得到时延估计值。设x1(t)的自相关函数为R11(τ),二次相关函数为RRR(τ),则

假设忽略信号与噪声之间的相关性,联立式(10)~式(12)即可得到

与互相关相同,当τ=D时,RRR(τ)取最大值,得到时延值。

广义互相关方法把已经得到的互相关函数转换到频域,对其频谱进行加权处理,以此抑制噪声的影响,再经过反变换到时域,得到广义互相关函数

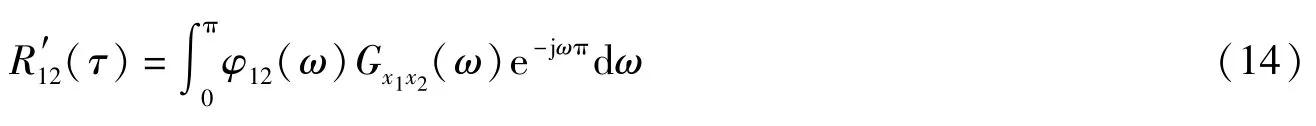
其中φ12(ω)为频域上的加权函数,Gx1x2(ω)为接收信号的互功率谱。

笔者使用的加权函数为平滑相干变换(SCOT:Smoothed Coherence Transform)函数,即利用平滑相干加权函数先对信号做预白化处理,再计算其互功率谱,在低信噪比情况下,SCOT法能有效解决由于信号波动对时延估计的影响[16]。SCOT函数如下

3 VMD-HD-GSCC算法

笔者提出的算法首先对接收信号经过VMD分解成K个模态分量,然后计算K个模态分量与原始信号的概率密度函数之间的豪斯多夫距离,利用豪斯多夫距离表示分量与原始信号之间的相似度,将HD增量最大的两个相邻模态分量作为突变点,突变点之前则为有效信号分量,其后则为噪声分量,以此进行信号重构,从而达到对信号进行去噪的目的,同时能较好地保持信号原有信息。将经过VMD处理后的信号作为新的信号,对其进行二次相关运算,得到二次相关函数,然后将其与SCOT函数相乘,能得到增强尖峰后的广义二次相关函数,最后进行峰值检测,获得时延估计值。流程图如图1所示。

图1 VMD-HD-GSCC算法流程图Fig.1 VMD-HD-GSCC algorithm flow chart

4 仿真实验与分析

实验采用的仿真信号为正弦信号x1(t),以及其延迟信号x2(t),信号幅度为5,采样频率Fs=1 kHz,采样点数N=1 024。假设两路信号延迟时间D=5 ms,即50个时间间隔,噪声是平稳高斯白噪声。两路信号的信噪比(SNR:Signal-Noise Ratio,RSNR)分别为RSNR1和RSNR2。假设噪声和信号之间,信号与信号之间无关。

实验分别对广义二次互相关时延估计算法(GSCC)、小波去噪结合广义二次互相关方法(WT-GSCC)和笔者提出算法—— 基于VMD分解的广义二次互相关时延估计算法(VMD-HD-GSCC)进行了仿真分析。对3种算法在信噪比于10 dB~-10 dB之间变化进行了实验,对比时延估计精度,实验结果如图2~图4所示。

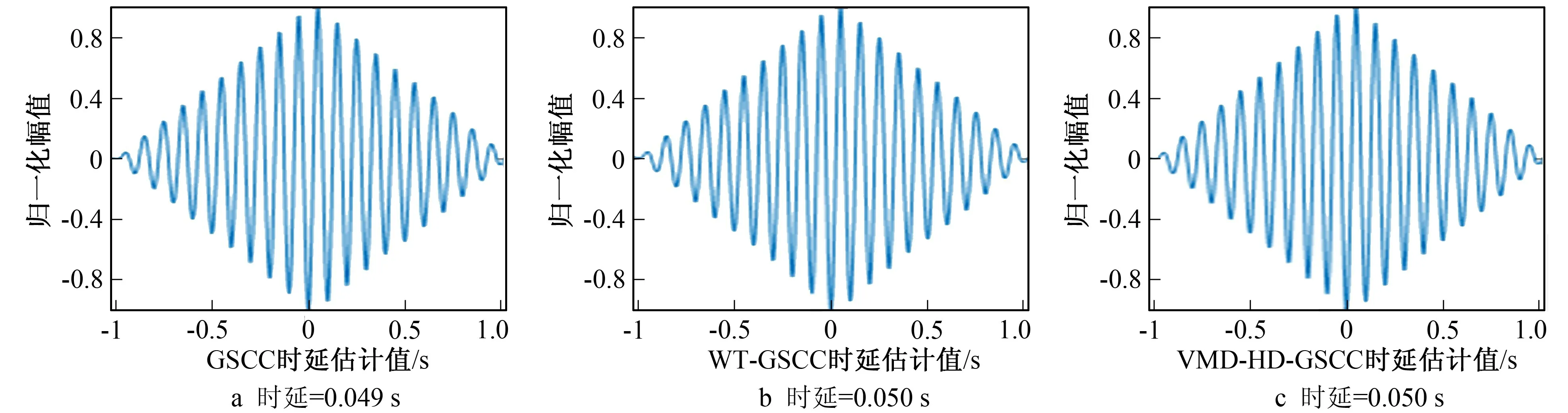
图2 R SNR=10 dB时3种算法的时延估计Fig.2 Time delay estimation of three algorithms when R SNR=10 dB

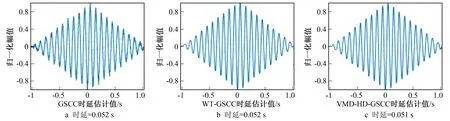
图3 R SNR=0时3种算法的时延估计仿真Fig.3 Time delay estimation of three algorithms when R SNR=0

如图2~图4所示,当RSNR=10 dB时,3种算法都具有良好的估计性能,相关函数峰值明显,时延估计值分别为49 ms,50 ms,50 ms,获得了准确的时延差值。当RSNR=0 dB时,3种算法的时延估计性能均不同程度受到了噪声影响,互相关函数的峰值也受到较大影响,时延估计值分别为52 ms,51 ms,51 ms。GSCC法在此时的时延估计图已经出现了较为严重的噪声,对估计的精度有一定影响。但相对WT-GSCC法和VMD-HD-GSCC法受到噪声的影响较小,并且还能稳定的估计出时延差值。当RSNR=-10 dB时,3种算法的时延估计性能都受到了较大影响,时延估计值分别为57 ms,47 ms,48 ms。可以看到,GSCC法的相关函数已经出现了多个相近峰值,噪声干扰过大,对时延估计的影响非常大,造成了较大的偏差,无法计算出合理的时延估计值。而WT-GSCC法和VMD-HD-GSCC法仍然保持良好的时延估计性能。

图4 R SNR=-10 dB时3种算法的时延估计仿真Fig.4 Time delay estimation of three algorithms when R SNR=-10 dB

对WT-GSCC法和VMD-HD-GSCC法随机进行信噪比为-10 dB对比试验,并对其结果进行局部放大,如图5所示,由于WT-GSCC法出现了多个相近峰值造成估计误差偏大,而VMD-HD-GSCC法出现的峰值尖锐且明显,时延估计的精度更高。

图5 WT-GSCC与VMD-HD-GSCC局部放大图Fig.5 Local enlarged view of WT-GSCC and VMD-HD-GSCC

随着噪声的不断增加,GSCC法时延估计性能逐渐减弱,时延估计精度不断降低。然而笔者提出的VMD-HD-GSCC法能保留良好的时延估计性能,而且大大改善了GSCC法在低信噪比下出现多个峰值的情况,在峰值附近有效消除了噪声干扰,提高了时延估计精度。

对以上3种时延估计算法分别进行N=30次的仿真实验,使用均方根误差(RMSE:Root Mean Square Error,ERMSE)作为评价指标评判各算法的时延估计性能,结果如图6所示。均方根误差定义式如下

图6 3种算法的性能对比Fig.6 Performance comparison of three algorithms

其中τi为预设时延估计值,τ为时延真实值。

当信噪比大于5 dB时,3种算法的估计性能相差不大,VMD-HD-GSCC法的时延估计性能略好于GSCC法和WT-GSCC法。当信噪比降低到5 dB以下时,GSCC法的性能明显变差,在信噪比为0时,WT-GSCC法的RMSE随着信噪比的降低而增大,而VMD-HD-GSCC法变化则较为缓慢,与其他两种算法相比证明其具有精确的时延估计精度以及良好的抗噪性能。

5 结 语

笔者提出的基于变分模态分解结合广义二次互相关时延估计算法,首先应用VMD方法能通过分离含噪信号中的噪声部分的特点,结合豪斯多夫距离优选模态并进行信号重构,实现了信号的预先去噪。然后将处理后的信号进行二次相关运算,将二次互相关函数与SCOT加权函数相乘,最后检测峰值得到时延估计值。

通过对3种算法在不同信噪比下的仿真实验,证明笔者算法具有良好的时延估计性能和抗噪性能,较好地保证了时延估计精度,具有广泛的应用前景。